第二十四章 圆解答题专项攻略(含答案)
图片预览
文档简介
中小学教育资源及组卷应用平台
第二十四章圆解答题专项攻略-2023-2024学年九年级上册人教版
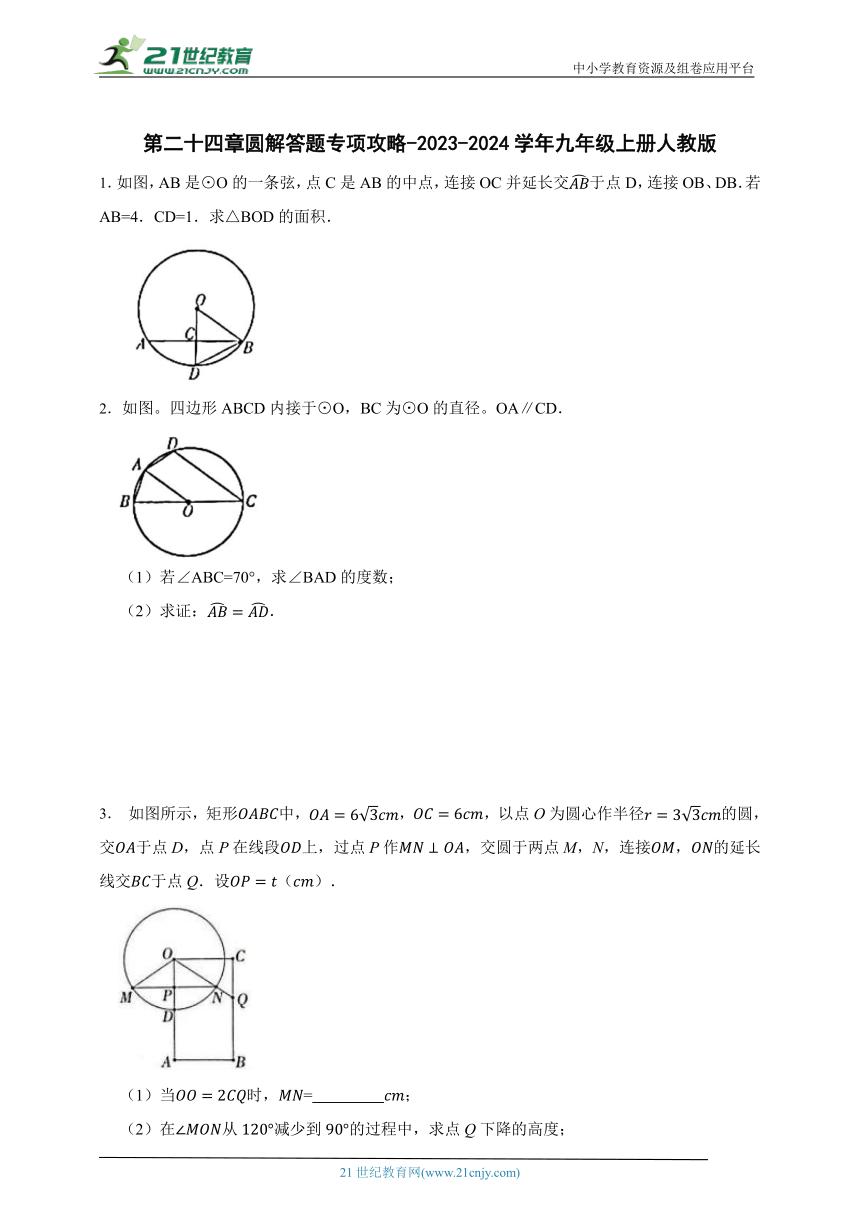
1.如图,AB是⊙O的一条弦,点C是AB的中点,连接OC并延长交于点D,连接OB、DB.若AB=4.CD=1.求△BOD的面积.
2.如图。四边形ABCD内接于⊙O,BC为⊙O的直径。OA∥CD.
(1)若∠ABC=70°,求∠BAD的度数;
(2)求证:.
3. 如图所示,矩形中,,,以点O为圆心作半径的圆,交于点D,点P在线段上,过点P作,交圆于两点M,N,连接,的延长线交于点Q.设().
(1)当时,= ;
(2)在从减少到的过程中,求点Q下降的高度;
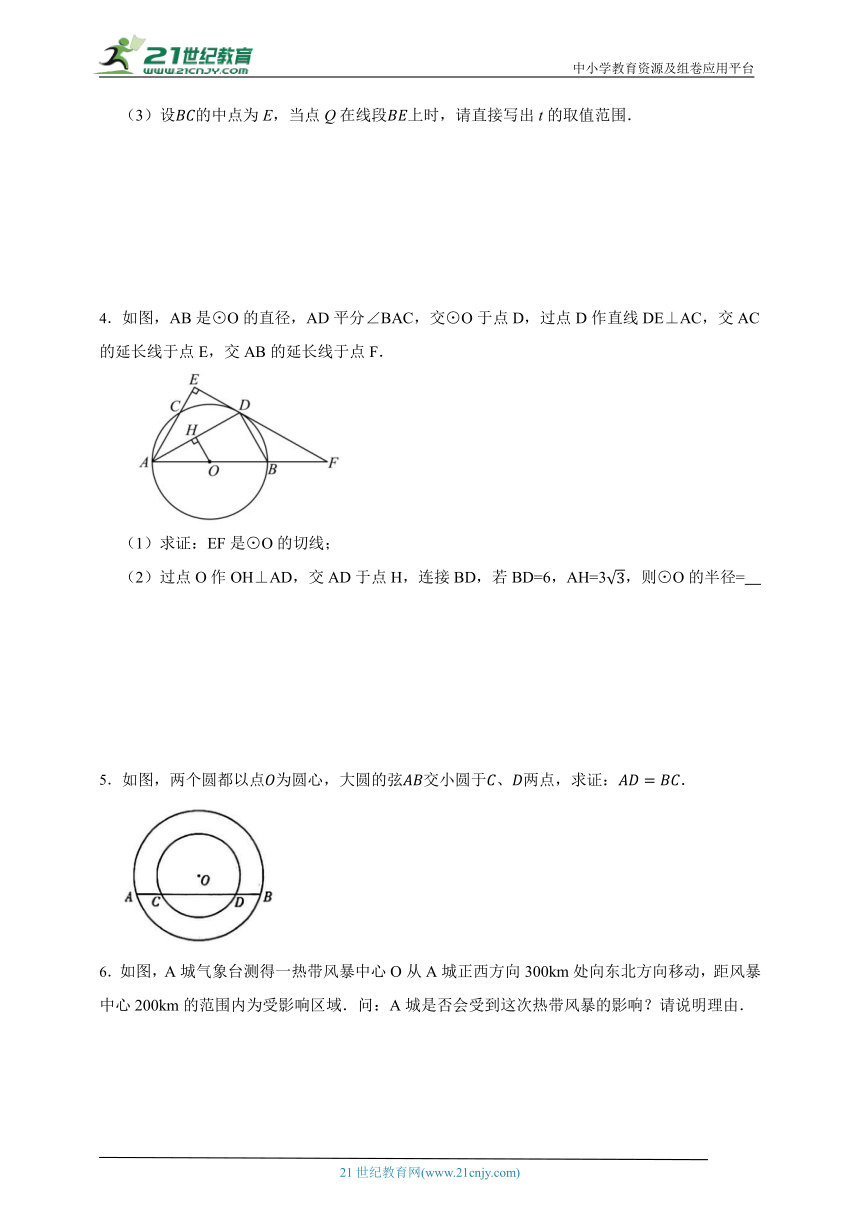
(3)设的中点为E,当点Q在线段上时,请直接写出t的取值范围.
4.如图,AB是⊙O的直径,AD平分∠BAC,交⊙O于点D,过点D作直线DE⊥AC,交AC的延长线于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)过点O作OH⊥AD,交AD于点H,连接BD,若BD=6,AH=3,则⊙O的半径=
5.如图,两个圆都以点为圆心,大圆的弦交小圆于、两点,求证:.
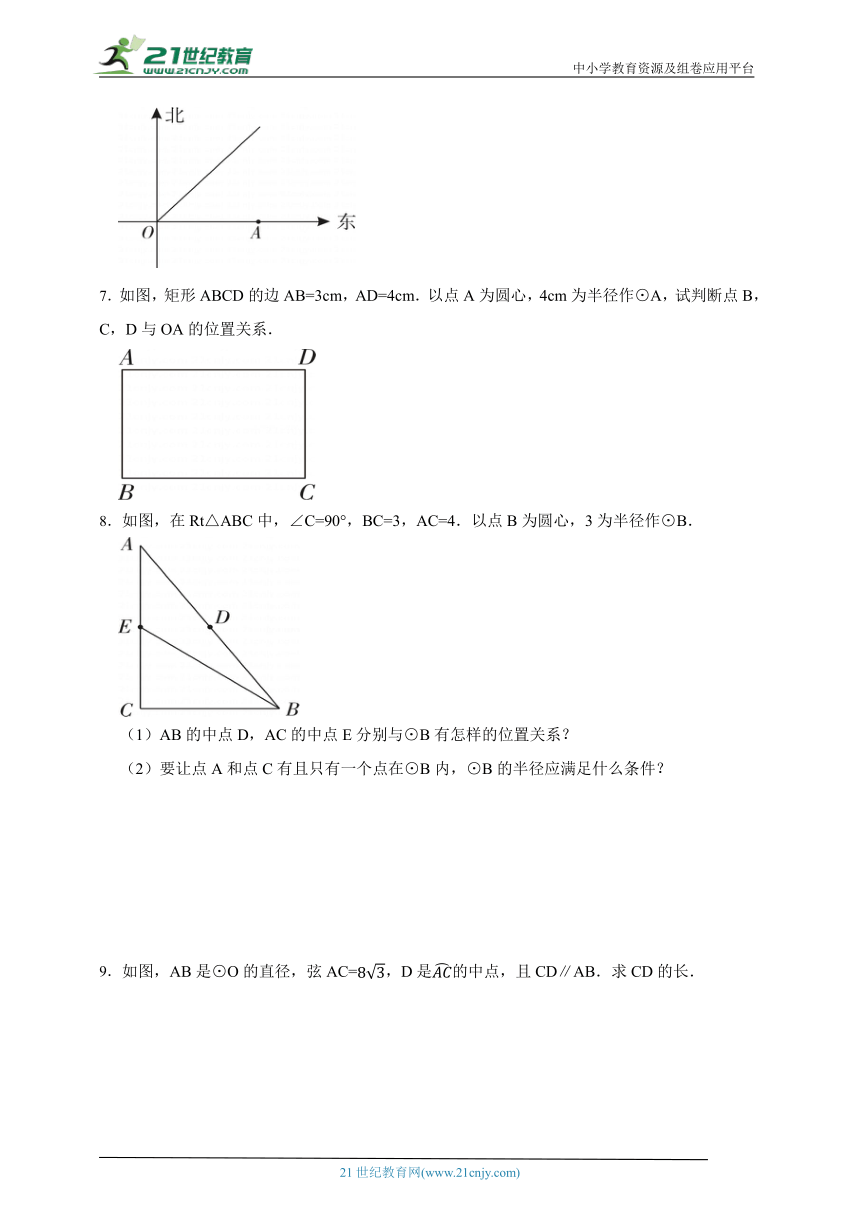
6.如图,A城气象台测得一热带风暴中心O从A城正西方向300km处向东北方向移动,距风暴中心200km的范围内为受影响区域.问:A城是否会受到这次热带风暴的影响?请说明理由.
7.如图,矩形ABCD的边AB=3cm,AD=4cm.以点A为圆心,4cm为半径作⊙A,试判断点B,C,D与OA的位置关系.
8.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4.以点B为圆心,3为半径作⊙B.
(1)AB的中点D,AC的中点E分别与⊙B有怎样的位置关系?
(2)要让点A和点C有且只有一个点在⊙B内,⊙B的半径应满足什么条件?
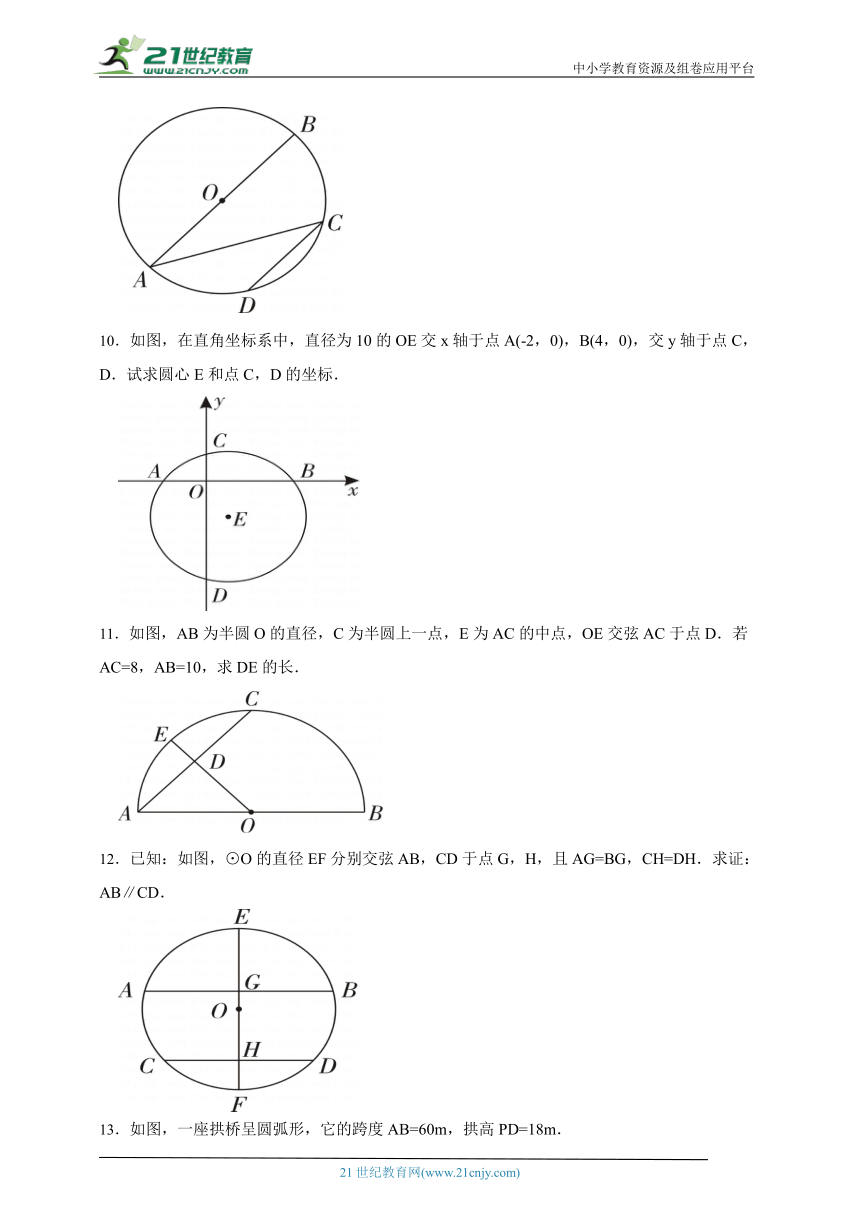
9.如图,AB是⊙O的直径,弦AC=,D是的中点,且CD∥AB.求CD的长.
10.如图,在直角坐标系中,直径为10的OE交x轴于点A(-2,0),B(4,0),交y轴于点C,D.试求圆心E和点C,D的坐标.
11.如图,AB为半圆O的直径,C为半圆上一点,E为AC的中点,OE交弦AC于点D.若AC=8,AB=10,求DE的长.
12.已知:如图,⊙O的直径EF分别交弦AB,CD于点G,H,且AG=BG,CH=DH.求证:AB∥CD.
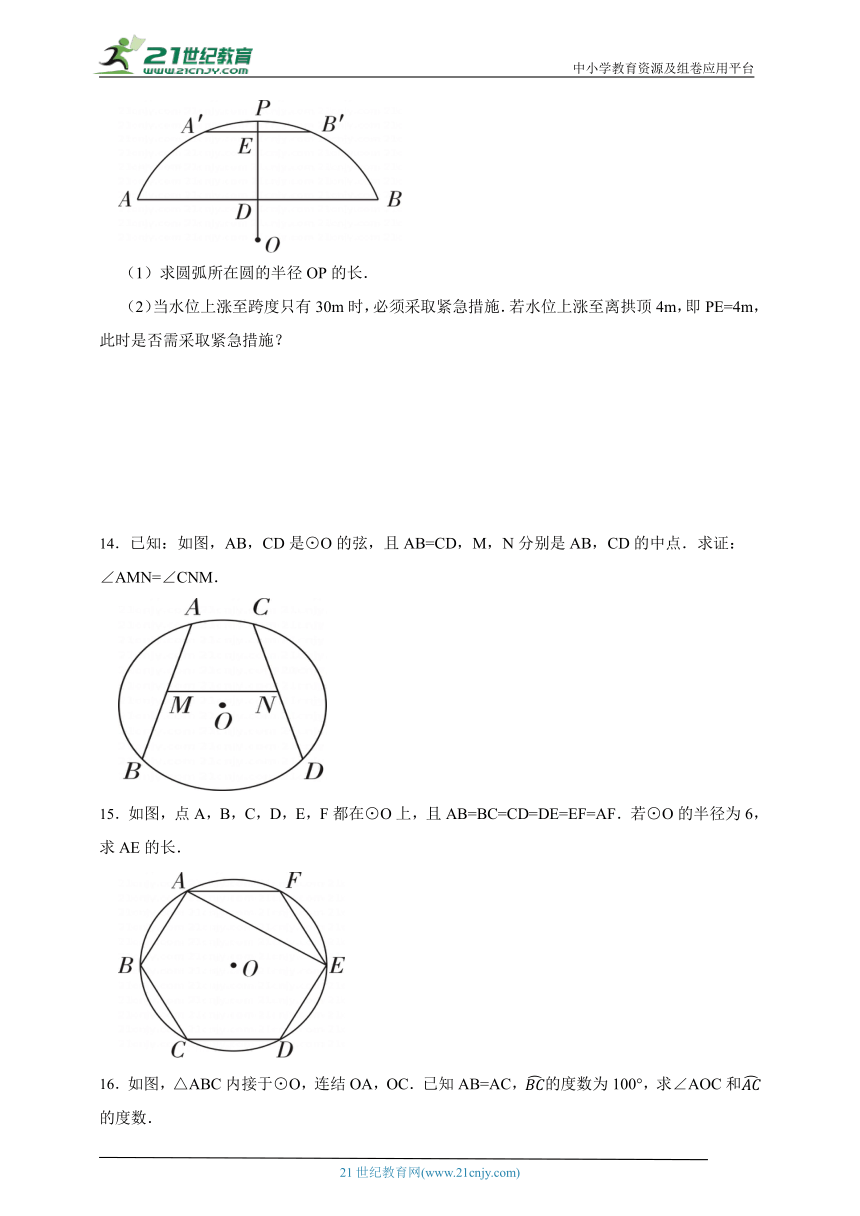
13.如图,一座拱桥呈圆弧形,它的跨度AB=60m,拱高PD=18m.
(1)求圆弧所在圆的半径OP的长.
(2)当水位上涨至跨度只有30m时,必须采取紧急措施.若水位上涨至离拱顶4m,即PE=4m,此时是否需采取紧急措施?
14.已知:如图,AB,CD是⊙O的弦,且AB=CD,M,N分别是AB,CD的中点.求证:∠AMN=∠CNM.
15.如图,点A,B,C,D,E,F都在⊙O上,且AB=BC=CD=DE=EF=AF.若⊙O的半径为6,求AE的长.
16.如图,△ABC内接于⊙O,连结OA,OC.已知AB=AC,的度数为100°,求∠AOC和的度数.
17.已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,在上取点G,连结CG,DG,AC.求证:∠DGC=2∠BAC.
18.如图,以 ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F.延长BA,交OA于点G.判断与是否相等,并说明理由.
19.已知:如图,在圆内接正五边形ABCDE中,对角线AC,BD交于点P.
(1)求∠APD的度数.
(2)求证:四边形EAPD是菱形.
20.已知:如图,正六边形ABCDEF的边长为6cm,延长FE,CD,相交于点G.
(1)求证:△FCG是正三角形.
(2)求正三角形FCG的高线长.
21.一个圆形人工湖如图①所示,弦AB是湖上的一座桥.已知AB长为100m,圆周角∠C=45°.求这个人工湖的直径.
方法一:如图②,延长BO,交⊙O于点E,连结AE,得Rt△BAE,∠E=∠C=45°,所以⊙O的直径BE=AB=100(m).
方法二:如图③,作AB的弦心距OH,连结OB,则∠BOH=∠C=45°.在Rt△OHB中,BH=AB=50(m),得OB=50(m),∴⊙O的直径=2OB=(m).
参考上面的解法,请你解决下面这个问题:
如图④,在直角坐标系中,已知点A(3,0),B(0,-3),C为直线AB上一点,过A,O,C的⊙E的半径为2.求线段OC的长.
答案解析部分
1.【答案】解:△BOD的面积是
2.【答案】(1)解:∠BAD = 140°.
(2)证明:连接OD,∵OC = OD,∴∠ODC =∠ OCD,∵OA∥CD,∴∠AOD = ∠ODC,∠AOB =∠ OCD,∴∠AOB =∠AOD,∴.
3.【答案】(1)
(2)解:在矩形中,,
∵,,
∴.
当时,,,
则,.
当时,,,
则,.
∴在从减少到的过程中,点O下降的高度为.
(3)解:
4.【答案】(1)证明:连接OD
∵DE⊥AC
∴∠E=90°
∵AD平分∠BAC
∴
∵OA=OD
∴
∴
∴EA∥DO
∴
∴EF是⊙O的切线
(2)6
5.【答案】解:过点O作,垂足为点P,
在小中,,
在大中,,,,
6.【答案】解:不会受影响.
过点A作AB⊥OB于点B,如图:
由题意可得,∠BOA=45°,
则BO=AB,
故AO2=BO2+AB2,
即3002=2AB2,
解得:;
∴A城不会受到这次热带风暴的影响.
7.【答案】解:连接AC,如图:
∵AB=3cm,AD=4cm,
∴cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外.
8.【答案】(1)解:∵∠C=90°,BC=3,AC=4,
∴,
∵D为AB的中点,
∴BD=2.5,
∴点D在圆B内,
∵BE>BC,即BE>3,
∴点E在圆B外.
(2)解:设圆B的半径为r,
当3<r≤5时,点A和点C有且只有一个点在圆B内.
9.【答案】解:连接OD,与AC交于点E,如图:
∵D是的中点,
∴OD垂直平分AC,
即AE=CE,∠AEO=∠CED=90°;
∵CD∥AB ,
∴∠OAC=∠ECD,
∴△AOE≌△CDE,
∴OE=DE,OA=CD,
∴OA=2OE,
在Rt△AOE中,OA2=OE2+AE2,
即,
解得:OE=4,
则OA=8,
∴CD=8.
10.【答案】解:过E作EF⊥AB于F,EG⊥CD于G,连接EB,CE,DE,如图:
∵A、B的坐标分别为(-2,0)、(4,0),
∴AB=6,OB=4,
∵EF⊥AB,
∴,
∴OF=1,
∵⊙E的直径为10,
∴半径EB=5,
∴,
∴E的坐标是(1,-4).
则EG=1,
∴,
则
∴点C的坐标是,
则
点D的坐标是.
11.【答案】解:∵E是弧AC的中点,
∴AC⊥OE,且,
∵AB=10,
∴,
在Rt△ADO中,,
∴DE=OE-OD=5-3=2.
12.【答案】证明:∵EF是⊙O的直径,AG=BG,
∴EF⊥AB;
又∵CH=DH,
∴EF⊥CD;
∴AB∥CD.
13.【答案】(1)解: 连接OA,如图:
由题意得:(米),OD=(r-18)米,
在Rt△ADO中,由勾股定理得:r2=302+(r-18)2,
解得:r=34(米);
即OP=34m.
(2)解: 连接OA′,
∵OE=OP-PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2-OE2,即:A′E2=342-302,
解得:A′E=16(米).
∴A′B′=32(米).
∵A′B′=32>30,
∴不需要采取紧急措施.
14.【答案】证明:连接OM、ON,
∵M、N分别为弦AB、CD的中点,点O是⊙O的圆心,
∴OM⊥AB,ON⊥CD.
∵AB=CD,
∴OM=ON.
∴∠OMN=∠ONM.
∵∠AMN=90°-∠OMN,
∵∠CNM=90°-∠ONM,
∴∠AMN=∠CNM.
15.【答案】解:连接AO, FO, EO, FO与AE交于点M,则∠AOF=∠EOF=60°.
∵ OA=OF= OE,
∴△AOF,△EOF都是等边三角形,
∴FO垂直平分AE,
在Rt△AOM中,∠AOF=60°,
则∠OAM=30°,
又∵OA=6,∴
∴AE=2AM=.
16.【答案】解:∵的度数是100°,
即∠BOC=100°,
∵AB=AC,
∴∠AOC=∠AOB,
则
即∠AOC的度数为130°,
∴的度数是130°.
17.【答案】证明:连结AD,如图:
∵CD⊥AB,
∴,
∴∠BAC=∠BAD,
则∠DAC=2∠BAC;
∵,
∴∠DGC=∠DAC,
∴∠DGC=2∠BAC.
18.【答案】解:连结AF,如图:
∵A为圆心,
∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AFB=∠DAF,∠GAD=∠ABF,
∴∠EAF=∠GAE,
∴.
19.【答案】(1)解:∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,
∴,
∴,
∴∠BPC=180°-2×36°=108°,
∴∠APD=∠BPC=108°,
(2)证明:∵五边形ABCDE是正五边形,
∴, AB=BC=CD=DE=AE,
∴∠ABP=∠ABC-∠DBC=108°-36°=72°;
则∠ABP+∠DBC=108°+72°=180°;
∴BD∥AE,
同理可得AC∥DE,
∴四边形DEAP是平行四边形,
∵AE=DE,
∴四边形EAPD是菱形.
20.【答案】(1)证明: ∵六边形ABCDEF是正六边形,
∴,
∴∠EDG=∠DEG=60°,
∴△EDG是正三角形,
∴∠G=60°,GE=GD,
又EF=DC,
∴GF=GC,
∴△FCG是正三角形;
(2)解:连接FD,
∵△EDG是正三角形,
∴DG=DE,
又∵DG=DC,
∴CD=DG=6,
又FC=FG,
∴FD⊥CG,
∴.
21.【答案】解:∵ A(3,0),B(0,-3) ,
即OA=OB,
则△AOB是等腰直角三角形,
∴∠OAB=45°;
延长OE交⊙E于点F,连结CF,得Rt△OCF,
则∠F=∠OAB=45°,∠OCF=90°;
∴OC=CF,
又∵⊙E的直径OF=4,
则,
即,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章圆解答题专项攻略-2023-2024学年九年级上册人教版
1.如图,AB是⊙O的一条弦,点C是AB的中点,连接OC并延长交于点D,连接OB、DB.若AB=4.CD=1.求△BOD的面积.
2.如图。四边形ABCD内接于⊙O,BC为⊙O的直径。OA∥CD.
(1)若∠ABC=70°,求∠BAD的度数;
(2)求证:.
3. 如图所示,矩形中,,,以点O为圆心作半径的圆,交于点D,点P在线段上,过点P作,交圆于两点M,N,连接,的延长线交于点Q.设().
(1)当时,= ;
(2)在从减少到的过程中,求点Q下降的高度;
(3)设的中点为E,当点Q在线段上时,请直接写出t的取值范围.
4.如图,AB是⊙O的直径,AD平分∠BAC,交⊙O于点D,过点D作直线DE⊥AC,交AC的延长线于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)过点O作OH⊥AD,交AD于点H,连接BD,若BD=6,AH=3,则⊙O的半径=
5.如图,两个圆都以点为圆心,大圆的弦交小圆于、两点,求证:.
6.如图,A城气象台测得一热带风暴中心O从A城正西方向300km处向东北方向移动,距风暴中心200km的范围内为受影响区域.问:A城是否会受到这次热带风暴的影响?请说明理由.
7.如图,矩形ABCD的边AB=3cm,AD=4cm.以点A为圆心,4cm为半径作⊙A,试判断点B,C,D与OA的位置关系.
8.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4.以点B为圆心,3为半径作⊙B.
(1)AB的中点D,AC的中点E分别与⊙B有怎样的位置关系?
(2)要让点A和点C有且只有一个点在⊙B内,⊙B的半径应满足什么条件?
9.如图,AB是⊙O的直径,弦AC=,D是的中点,且CD∥AB.求CD的长.
10.如图,在直角坐标系中,直径为10的OE交x轴于点A(-2,0),B(4,0),交y轴于点C,D.试求圆心E和点C,D的坐标.
11.如图,AB为半圆O的直径,C为半圆上一点,E为AC的中点,OE交弦AC于点D.若AC=8,AB=10,求DE的长.
12.已知:如图,⊙O的直径EF分别交弦AB,CD于点G,H,且AG=BG,CH=DH.求证:AB∥CD.
13.如图,一座拱桥呈圆弧形,它的跨度AB=60m,拱高PD=18m.
(1)求圆弧所在圆的半径OP的长.
(2)当水位上涨至跨度只有30m时,必须采取紧急措施.若水位上涨至离拱顶4m,即PE=4m,此时是否需采取紧急措施?
14.已知:如图,AB,CD是⊙O的弦,且AB=CD,M,N分别是AB,CD的中点.求证:∠AMN=∠CNM.
15.如图,点A,B,C,D,E,F都在⊙O上,且AB=BC=CD=DE=EF=AF.若⊙O的半径为6,求AE的长.
16.如图,△ABC内接于⊙O,连结OA,OC.已知AB=AC,的度数为100°,求∠AOC和的度数.
17.已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,在上取点G,连结CG,DG,AC.求证:∠DGC=2∠BAC.
18.如图,以 ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F.延长BA,交OA于点G.判断与是否相等,并说明理由.
19.已知:如图,在圆内接正五边形ABCDE中,对角线AC,BD交于点P.
(1)求∠APD的度数.
(2)求证:四边形EAPD是菱形.
20.已知:如图,正六边形ABCDEF的边长为6cm,延长FE,CD,相交于点G.
(1)求证:△FCG是正三角形.
(2)求正三角形FCG的高线长.
21.一个圆形人工湖如图①所示,弦AB是湖上的一座桥.已知AB长为100m,圆周角∠C=45°.求这个人工湖的直径.
方法一:如图②,延长BO,交⊙O于点E,连结AE,得Rt△BAE,∠E=∠C=45°,所以⊙O的直径BE=AB=100(m).
方法二:如图③,作AB的弦心距OH,连结OB,则∠BOH=∠C=45°.在Rt△OHB中,BH=AB=50(m),得OB=50(m),∴⊙O的直径=2OB=(m).
参考上面的解法,请你解决下面这个问题:
如图④,在直角坐标系中,已知点A(3,0),B(0,-3),C为直线AB上一点,过A,O,C的⊙E的半径为2.求线段OC的长.
答案解析部分
1.【答案】解:△BOD的面积是
2.【答案】(1)解:∠BAD = 140°.
(2)证明:连接OD,∵OC = OD,∴∠ODC =∠ OCD,∵OA∥CD,∴∠AOD = ∠ODC,∠AOB =∠ OCD,∴∠AOB =∠AOD,∴.
3.【答案】(1)
(2)解:在矩形中,,
∵,,
∴.
当时,,,
则,.
当时,,,
则,.
∴在从减少到的过程中,点O下降的高度为.
(3)解:
4.【答案】(1)证明:连接OD
∵DE⊥AC
∴∠E=90°
∵AD平分∠BAC
∴
∵OA=OD
∴
∴
∴EA∥DO
∴
∴EF是⊙O的切线
(2)6
5.【答案】解:过点O作,垂足为点P,
在小中,,
在大中,,,,
6.【答案】解:不会受影响.
过点A作AB⊥OB于点B,如图:
由题意可得,∠BOA=45°,
则BO=AB,
故AO2=BO2+AB2,
即3002=2AB2,
解得:;
∴A城不会受到这次热带风暴的影响.
7.【答案】解:连接AC,如图:
∵AB=3cm,AD=4cm,
∴cm,
∴点B在⊙A内,点D在⊙A上,点C在⊙A外.
8.【答案】(1)解:∵∠C=90°,BC=3,AC=4,
∴,
∵D为AB的中点,
∴BD=2.5,
∴点D在圆B内,
∵BE>BC,即BE>3,
∴点E在圆B外.
(2)解:设圆B的半径为r,
当3<r≤5时,点A和点C有且只有一个点在圆B内.
9.【答案】解:连接OD,与AC交于点E,如图:
∵D是的中点,
∴OD垂直平分AC,
即AE=CE,∠AEO=∠CED=90°;
∵CD∥AB ,
∴∠OAC=∠ECD,
∴△AOE≌△CDE,
∴OE=DE,OA=CD,
∴OA=2OE,
在Rt△AOE中,OA2=OE2+AE2,
即,
解得:OE=4,
则OA=8,
∴CD=8.
10.【答案】解:过E作EF⊥AB于F,EG⊥CD于G,连接EB,CE,DE,如图:
∵A、B的坐标分别为(-2,0)、(4,0),
∴AB=6,OB=4,
∵EF⊥AB,
∴,
∴OF=1,
∵⊙E的直径为10,
∴半径EB=5,
∴,
∴E的坐标是(1,-4).
则EG=1,
∴,
则
∴点C的坐标是,
则
点D的坐标是.
11.【答案】解:∵E是弧AC的中点,
∴AC⊥OE,且,
∵AB=10,
∴,
在Rt△ADO中,,
∴DE=OE-OD=5-3=2.
12.【答案】证明:∵EF是⊙O的直径,AG=BG,
∴EF⊥AB;
又∵CH=DH,
∴EF⊥CD;
∴AB∥CD.
13.【答案】(1)解: 连接OA,如图:
由题意得:(米),OD=(r-18)米,
在Rt△ADO中,由勾股定理得:r2=302+(r-18)2,
解得:r=34(米);
即OP=34m.
(2)解: 连接OA′,
∵OE=OP-PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2-OE2,即:A′E2=342-302,
解得:A′E=16(米).
∴A′B′=32(米).
∵A′B′=32>30,
∴不需要采取紧急措施.
14.【答案】证明:连接OM、ON,
∵M、N分别为弦AB、CD的中点,点O是⊙O的圆心,
∴OM⊥AB,ON⊥CD.
∵AB=CD,
∴OM=ON.
∴∠OMN=∠ONM.
∵∠AMN=90°-∠OMN,
∵∠CNM=90°-∠ONM,
∴∠AMN=∠CNM.
15.【答案】解:连接AO, FO, EO, FO与AE交于点M,则∠AOF=∠EOF=60°.
∵ OA=OF= OE,
∴△AOF,△EOF都是等边三角形,
∴FO垂直平分AE,
在Rt△AOM中,∠AOF=60°,
则∠OAM=30°,
又∵OA=6,∴
∴AE=2AM=.
16.【答案】解:∵的度数是100°,
即∠BOC=100°,
∵AB=AC,
∴∠AOC=∠AOB,
则
即∠AOC的度数为130°,
∴的度数是130°.
17.【答案】证明:连结AD,如图:
∵CD⊥AB,
∴,
∴∠BAC=∠BAD,
则∠DAC=2∠BAC;
∵,
∴∠DGC=∠DAC,
∴∠DGC=2∠BAC.
18.【答案】解:连结AF,如图:
∵A为圆心,
∴AB=AF,
∴∠ABF=∠AFB,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠AFB=∠DAF,∠GAD=∠ABF,
∴∠EAF=∠GAE,
∴.
19.【答案】(1)解:∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,
∴,
∴,
∴∠BPC=180°-2×36°=108°,
∴∠APD=∠BPC=108°,
(2)证明:∵五边形ABCDE是正五边形,
∴, AB=BC=CD=DE=AE,
∴∠ABP=∠ABC-∠DBC=108°-36°=72°;
则∠ABP+∠DBC=108°+72°=180°;
∴BD∥AE,
同理可得AC∥DE,
∴四边形DEAP是平行四边形,
∵AE=DE,
∴四边形EAPD是菱形.
20.【答案】(1)证明: ∵六边形ABCDEF是正六边形,
∴,
∴∠EDG=∠DEG=60°,
∴△EDG是正三角形,
∴∠G=60°,GE=GD,
又EF=DC,
∴GF=GC,
∴△FCG是正三角形;
(2)解:连接FD,
∵△EDG是正三角形,
∴DG=DE,
又∵DG=DC,
∴CD=DG=6,
又FC=FG,
∴FD⊥CG,
∴.
21.【答案】解:∵ A(3,0),B(0,-3) ,
即OA=OB,
则△AOB是等腰直角三角形,
∴∠OAB=45°;
延长OE交⊙E于点F,连结CF,得Rt△OCF,
则∠F=∠OAB=45°,∠OCF=90°;
∴OC=CF,
又∵⊙E的直径OF=4,
则,
即,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
