第二十一章 一元二次方程解答题专项特训(含解析)
文档属性
| 名称 | 第二十一章 一元二次方程解答题专项特训(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 13:25:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十一章一元二次方程解答题专项特训-数学九年级上册人教版
1.阅读下面的例题,解方程的过程如下:
①当时,原方程化为,解得:(舍去).
②当时,原方程可化为,解得:(舍去).
原方程的解:.
请参照例题解方程:.
2.已知关于的一元二次方程有两个实数根.
(1)求的取值范围;
(2)如果方程的两个实数根为,且,求的值.
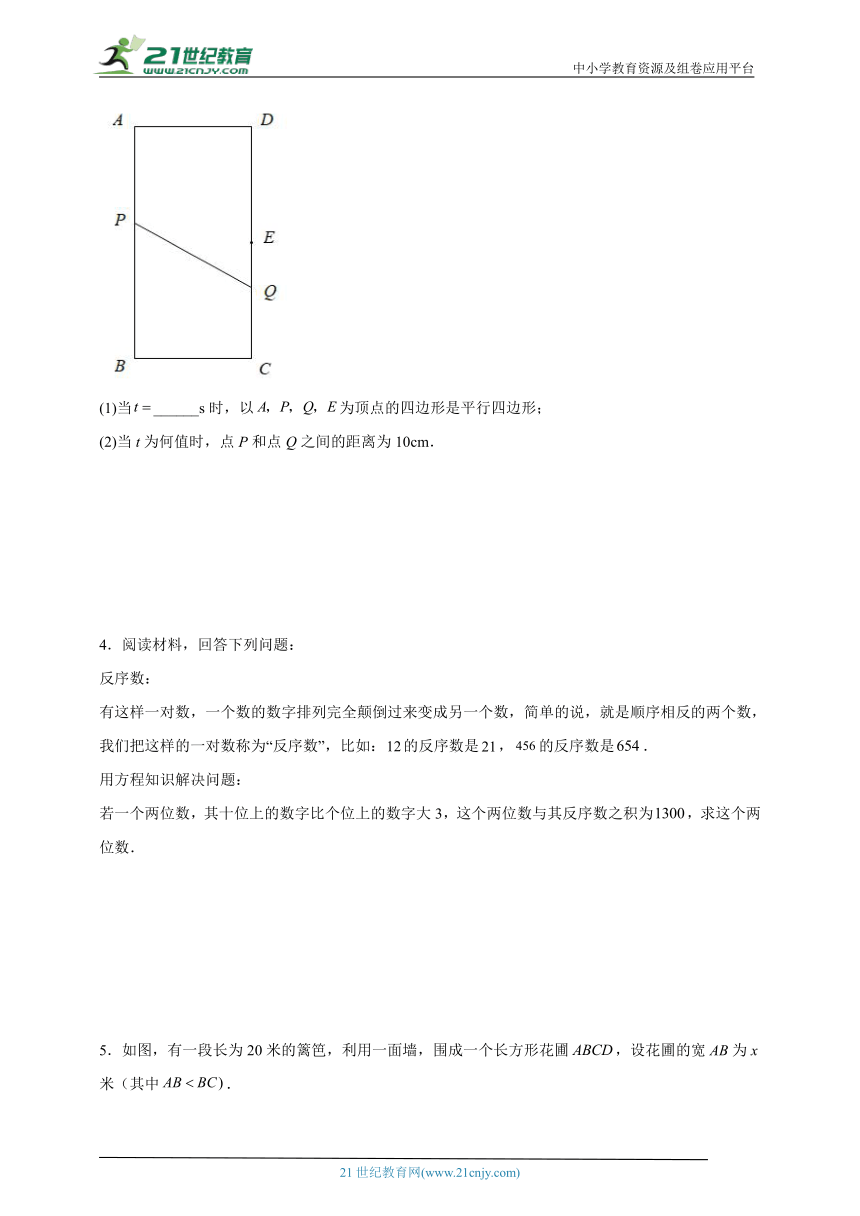
3.如图,在矩形中,点是的中点,,,动点P从点A出发,以3cm/s的速度向点B运动,到达点B时停止运动;动点Q同时从点C出发,以2cm/s的速度向点D运动.设运动的时间为t s.
(1)当______s时,以为顶点的四边形是平行四边形;
(2)当t为何值时,点P和点Q之间的距离为10cm.
4.阅读材料,回答下列问题:
反序数:
有这样一对数,一个数的数字排列完全颠倒过来变成另一个数,简单的说,就是顺序相反的两个数,我们把这样的一对数称为“反序数”,比如:的反序数是,的反序数是.
用方程知识解决问题:
若一个两位数,其十位上的数字比个位上的数字大3,这个两位数与其反序数之积为,求这个两位数.
5.如图,有一段长为20米的篱笆,利用一面墙,围成一个长方形花圃,设花圃的宽AB为x米(其中.
(1)请你用含x的代数式表示BC的长.
(2)若此时花圃的面积刚好为,求此时花圃的宽AB的长度.
6.古算趣题:“笨伯执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭,有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足,借问竿长多少数,谁人算出我佩服”.其大意是:笨伯拿竹竿进屋,横拿竖拿都进不去,横着比门宽4尺,竖着比门高2尺.他的邻居教他沿着门的对角线斜着拿竿,笨伯一试,刚好进去.问:竹竿有多少尺?
7.如图,要把长为、宽为的长方形花坛四周扩展相同的宽度,得到面积为的新长方形花坛,求扩展的宽度.
8.(换元法)解方程:
解:设则原方程可化为
解得:
当时,,解得
当时,,解得
∴原方程的根是,
根据以上材料,请解方程:
(1).
(2)
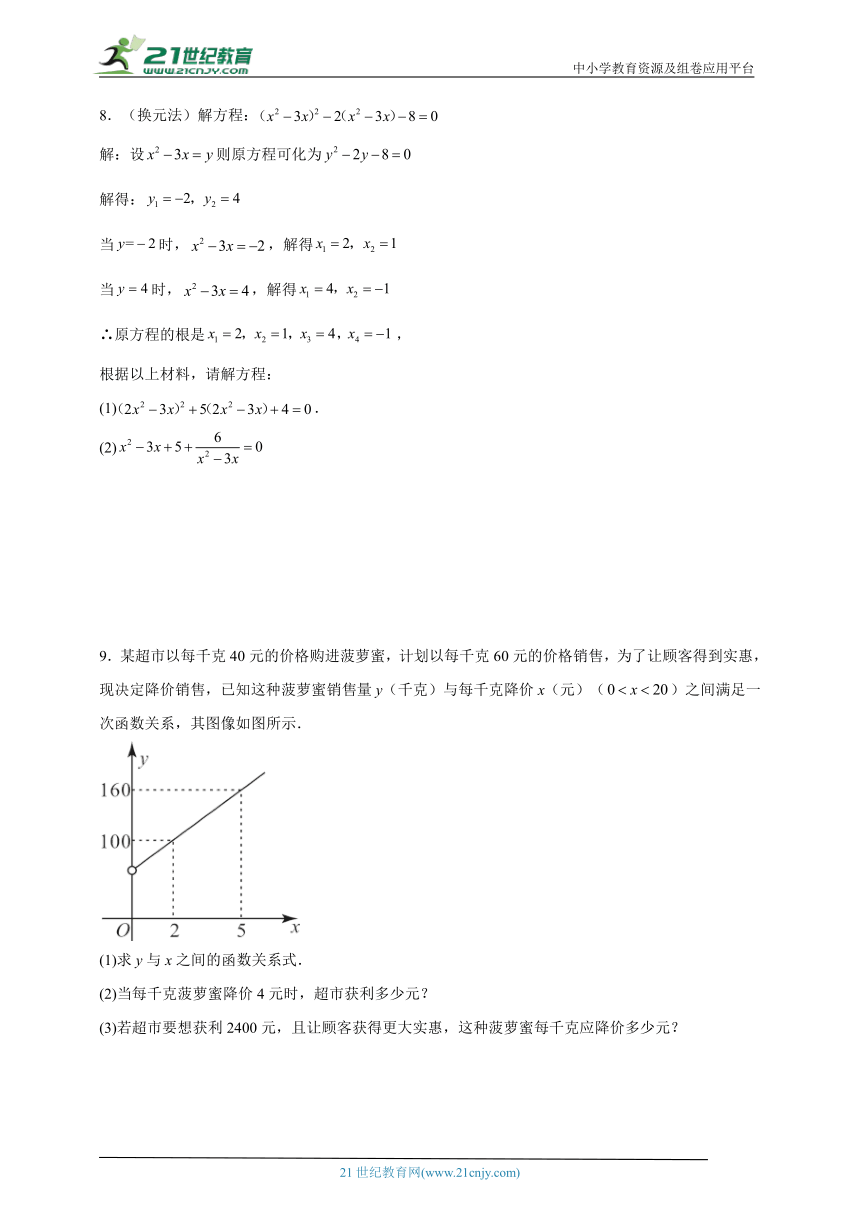
9.某超市以每千克40元的价格购进菠萝蜜,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种菠萝蜜销售量y(千克)与每千克降价x(元)()之间满足一次函数关系,其图像如图所示.
(1)求y与x之间的函数关系式.
(2)当每千克菠萝蜜降价4元时,超市获利多少元?
(3)若超市要想获利2400元,且让顾客获得更大实惠,这种菠萝蜜每千克应降价多少元?
10.阅读材料,解答问题.
阅读材料:
为解方程,我们可以将视为一个整体;然后设,则,原方程化为.①
解得,.
当时,,,,
当时,,,.
原方程的解为,,,.
解答问题:
(1)填空在由原方程得到方程①的过程中,利用________法达到了降次的目的;体现了________的数学思想.
(2)解方程.
11.如图,已知等腰三角形,,,点从点出发,沿的方向以的速度向终点运动,同时点从点出发,沿的方向以的速度向终点运动,当点运动到点时,两点均停止运动,运动时间记为秒,请解决下列问题:
(1)若点在边上,当为何值时,?
(2)是否存在这样的值,使的面积为?若存在,请求出的值,若不存在,请说明理由.
12.某超市销售一种商品,每件盈利50元,平均每天可达到30件.为尽快减少库存,现在准备降价促销.经调查发现:一件商品降价1元平均每天可以多销售2件.
(1)当一件商品降价5元时,每天的销售量可达到_____________件,每天共盈利_______________元;
(2)在上述条件不变、销售正常的情况下,每件商品降价多少元该超市每天的盈利为2100元,同时也更加优惠?
13.由于疫情反弹,某地区开展了连续全员核酸检测,9月7日,医院派出13名医护人员到一个大型小区设置了、两个采样点进行核酸采样,当天共采样9220份,已知点平均每人采样720份,点平均每人采样700份.
(1)求、两点各有多少名医护人员?
(2)9月8日,医院继续派出这13名医护人员前往这个小区进行核酸采样,这天,社区组织者将附近数个商户也纳入这个小区采样范围,同时重新规划,决定从点抽调部分医护人员到点经调查发现,点每减少1名医护人员,人均采样量增加10份,点人均采样量不变,最后当天共采样9360份,求从点抽调了多少名医护人员到点?
14.六一节前某市场以每盒60元的价格购进1000盒拼装玩具.四月份以单价100元销售,售出了300盒.五月份如果销售单价不变,预计仍可售出300盒,市场为增加销售量,决定降价销售,根据市场调查,销售单价每降低3元,可多售出6盒,但最低销售单价应高于购进的价格.五月份结束后,批发商将对剩余的玩具一次性清仓,清仓时销售单价为50元.设五月份销售单价降低x元.
(1)填空:五月销售量为______件,清仓销售量为______件.
(2)如果市场希望通过销售这批玩具获利15200元,那么五月份的销售单价应是多少元?
15.某演出团体准备在常州大剧院举办迎新演出,该剧院共有1500个座位.如果票价定为每张100元,那么门票可以全部售出;如果票价每增加1元/张,那么门票就会减少3张.演出团体既要让利于民又要使得门票收入为240000元,则票价应该定为多少元/张?
16.新年到了,为增进同学友谊,某班主任规定本班同学间,每两个人必须相互通电话1次
(1)若本班人数为20,则共通话________次,若本班人数为(,且为正整数),则共通话________次;
(2)若同学们共通话1225次,求该班同学的人数;
(3)王峰同学由打电话问题想到了一个数学问题:若线段上共有个点(不含端点、),线段总数为多少呢?请直接写出结论.
17.某商场销售一批空气加湿器,平均每天可售出30台,每台可盈利50元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每台降价1元,商场平均每天可多售出2台.
(1)若该商场某天降价了5元,则当天可售出 台,当天共盈利 元;
(2)在尽快减少库存的前提下,商场每天要盈利2100元,每台空气加湿器应降价多少元?
18.年卡塔尔世界杯吉祥物,中文名是拉伊卜,代表着技艺高超的球员.随着世界杯的火热进行,吉祥物拉伊卜玩偶成为畅销商品.某经销商售卖大、小两种拉伊卜玩偶,大拉伊卜售价是小拉伊卜售价的倍且元购买小拉伊卜玩偶的数量比购买大拉伊卜玩偶的数量多个.
(1)求小、大拉伊卜玩偶售价分别为多少元?
(2)世界杯开赛第一周该经销商售出小拉伊卜玩偶个,大拉伊卜玩偶个,世界杯开赛第二周,该经销商决定降价出售两种拉伊卜玩偶.已知:两种拉伊卜玩偶都降价元,小拉伊卜玩偶售出数量较世界杯开赛第一周多了个:大拉伊卜玩偶售出数量与世界杯开赛第一周相同,该经销商世界杯第二周总销售额为元,求的值.
19.已知的三条边分别是.
(1)判断的值的正负.
(2)若满足,判断的形状.
20.如图,中,,,,一动点P从点C出发沿着方向以的速度运动,另一动点Q从A出发沿着边以的速度运动,P,Q两点同时出发,运动时间为.
(1)若的面积是面积的,求t的值?
(2)的面积能否为面积的一半?若能,求出t的值;若不能,说明理由.
参考答案:
1.
【分析】分和,两种情况进行讨论求解即可.
【详解】解:当时,原方程化为,解得:(舍去).
当时,原方程可化为,解得:(舍去).
原方程的解:.
【点睛】本题考查解一元二次方程.理解并掌握题干中给出的解方程的方法,是解题的关键.
2.(1)
(2)
【分析】(1)根据一元二次方程根的判别式进行求解即可;
(2)根据一元二次方程根与系数的关系得到,,再由完全平方公式的变形得到,由此解方程即可得到答案.
【详解】(1)解:根据题意,得,即,
∴;
(2)解:由根与系数的关系,得,,
∵,
∴,即,
解得(舍去), .
∴的值为.
【点睛】本题主要考查了一元二次方程根的判别式,根与系数的关系,解一元二次方程,完全平方公式的变形求值,灵活运用所学知识是解题的关键.
3.(1)
(2)或
【分析】(1)利用平行四边形的性质得出当时,四边形为平行四边形求出即可;
(2)设当秒时cm,利用勾股定理得出即可;
【详解】(1)解:如图,
当四边形为平行四边形时,则,
,
解得
当s时,以为顶点的四边形是平行四边形;
(2)解:设运动时间为s,由题意得,.
①如图1,当点P在点Q的上方时,过点P作于点M.
在中,,,,
由勾股定理得,即,解得.
②如图2,当点P在点Q的下方时,过点P作于点N.
在中,,,.
由勾股定理得,即,解得.
由得符合题意.
综上得或.
【点睛】本题主要考查了平行四边形的性质及勾股定理和一元二次方程的应用等知识,熟练应用平行四边形的性质是解题关键.
4.
【分析】设这个两位数的个位数字为x,则十位数字为,根据这个两位数与其反序数之积为,可得出关于x的一元二次方程,解之取其符合题意的值,即可得出结论.
【详解】解:设这个两位数的个位数字为x,则十位数字为,
根据题意得:,
∴,即,
∴,
∴
解得或(舍去),
∴,
∴这个两位数为.
【点睛】本题主要考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
5.(1)
(2)3
【分析】(1)根据题意,求解即可;
(2)根据题意,列出一元二次方程,求解即可.
【详解】(1)解:∵篱笆的全长为20米,花圃的宽AB为x米,
的长为米;
(2)解:根据题意得:,
整理得:,
解得:,,
当时,,符合题意;
当时,,不符合题意,舍去.
答:此时花圃的宽AB的长度是3米.
【点睛】此题考查了一元二次方程的应用,解题的关键是理解题意,找到等量关系,正确列出方程.
6.10尺
【分析】设竹竿的长为尺,根据横着比门宽4尺,竖着比门高2尺,得到两条直角边长分别为尺和尺,根据沿对角线斜着拿竿,笨伯一试,刚好进去得到直角三角形斜边为尺,根据勾股定理列方程,解方程即可.
【详解】解:设竹竿的长为尺,根据题意,得
.
解这个方程,得,.
当时,,,不符合题意,舍去,
.
答:竹竿的长为10尺.
【点睛】此题考查了勾股定理和一元二次方程的应用,读懂题意,根据勾股定理列出一元二次方程是解题的关键.
7.扩展的宽度为
【分析】利用长方形的面积计算公式,结合新长方形花坛的面积为,即可得出关于的一元二次方程,解之取其正值即可得出结论.
【详解】解:设扩展的宽度为,
依题意,得:,
整理得:,
解得:,(不合题意,舍去).
答:扩展的宽度为.
【点睛】本题考查了一元二次方程的应用.找准等量关系,正确列出一元二次方程是解题的关键.
8.(1)原方程的根是;
(2)原方程的根是.
【分析】(1)设,则原方程可化为,解得的值,即可得到原方程的根;
(2)设,则原方程可化为,解得的值,检验后即可得到原方程的根.
【详解】(1)设,则原方程可化为
解得∶
当时,,解得
当时,,方程无解
原方程的根是;
(2)设,则原方程可化为
去分母,可得
解得
当时,,解得
当时,,方程无解
经检验∶都是原方程的解
原方程的根是.
【点睛】本题主要考查了运用换元法解一元二次方程以及分式方程,解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法.
9.(1)
(2)2240元
(3)12元
【分析】(1)运用待定系数法求解即可.
(2)先计算每千克菠萝蜜的利润,乘以销售量即可.
(3)列方程求解,且取较大值.
【详解】(1)设y与x之间的函数关系式为,
将,代入,
得,
解得,
∴y与x之间的函数关系式为.
(2)(元).
答:当每千克菠萝蜜降价4元时,超市获利2240元.
(3)依题意,得,
整理,得,
解得,.
∵要让顾客获得更大实惠,∴.
答:这种菠萝蜜每千克应降价12元.
【点睛】本题考查了一次函数的解析式及其应用,一元二次方程的解法,熟练掌握待定系数法,解方程是解题的关键.
10.(1)换元,转化
(2)
【分析】(1)题目中的方法用的是换元法,体现了转化的数学思想;
(2)令,得,用因式分解法解方程求出a的值,再求出x的值.
【详解】(1)解:在由原方程得到方程①的过程中,利用换元法达到了降幂的目的,体现了转化的数学思想,
故答案为:换元,转化;
(2)解:令,则原方程变为,
∴,
解得或,
∵,
∴,
∴,
∴.
【点睛】本题考查用换元法解一元二次方程,解题的关键是掌握换元法解一元二次方程的方法.
11.(1),当时
(2)存在;当或时,的面积为
【分析】(1)先根据已知条件求出的长度,再设经过 秒,是直角三角形,此时, ,当,,解方程即可;
(2)设经过秒,的面积为,连接,作于,分类讨论点在边上和点在边上,,即可求解.
【详解】(1)解:过点作,如图所示:
∵等腰三角形,,,
∴,
∴,
∴,
设经过秒,是直角三角形,则
, ,
当时,如图所示:
∴,
∴,
解得:,
若点在边上,当时
(2)存在,理由如下:
当点在边上,连接,过点作于,如图所示:
设经过秒,的面积为,则
, ,
∴,
∴,
∴,
解得:,(舍),
当点在边上,连接,,作于,如图所示:
设经过秒,的面积为,则
,,
∴,
∴,
∴,
解得:,(舍去),
∴当或时,的面积为.
【点睛】本题考查了一元二次方程、一元一次方程的应用和三角形与动点问题的综合,分类讨论思想和数形结合的思想是解决本题的关键.
12.(1),
(2)销售正常情况下,每件商品降价20元时超市每天盈利可达到2100元,同时也更加优惠.
【分析】(1)根据“一件商品每降价1元平均每天可多售出2件”即可求出每天销售量,根据销售量乘以每件盈利即可得到每天共盈利的钱数;
(2)设每件商品降价x元时超市每天盈利可达到2100元,根据销售量乘以每件盈利即可得到每天共盈利总数,列出方程求解即可.
【详解】(1)解:当一件商品降价5元时,每天销售量可达到(件),
每天共盈利(元),
故答案为:,;
(2)解:设每件商品降价元时超市每天盈利可达到元,
由题意得,,
解得,
根据题意,符合题意,
答:销售正常情况下,每件商品降价元时超市每天盈利可达到元,同时也更加优惠.
【点睛】此题考查了一元二次方程的应用,读懂题意,正确列出方程是解题的关键.
13.(1)A检测队有6人,B检测队有7人
(2)从B检测队中抽调了2人到A检测队
【分析】(1)设A点有x名医护人员,B点有y名医护人员,根据“A、B两个采样点共13名医护人员,且当天共采样9220份”,即可得出关于x,y的且当天共采样9220份,即可得出关于x, y的二元一次方程组,解之即可得出结论;
(2)设从B点抽调了m名医护人员到A点,则B点平均每人采样份,根据重新规划后当天共采样9360份,即可得出关于m的一元_二次方程,解之取其符合题意的值,即可得出结论.
【详解】(1)解:设A检测队有人,B检测队有人,
依题意得:,分解得:
答:A检测队有6人,B检测队有7人;
(2)解:设从B检测队中抽调了人到A检测队,则B检测队人均采样人,
依题意得:,
解得:,解得:,,
由于从B对抽调部分人到A检测队,则故,
答:从B检测队中抽调了2人到A检测队.
【点睛】本题考查了二元一次方程组的应用以及一元二次方程的应用,解题的关键是:(1)找准等关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元二次方程.
14.(1),
(2)五月份的销售单价应是80元
【分析】(1)设五月份销售单价降低x元,则十月份销售单价为元,再根据销售单价每降低3元,可多售出6盒求出五月份的销售量即可求出清仓销售的数量;
(2)根据“销售这批玩具获利15200元”,列出方程,即可求解.
【详解】(1)解:设五月份销售单价降低x元,则
五月份销售单价为元, 销售量为件,
五月份结束后,剩余的玩具的数量为件,
故答案为:,
(2)解:依题意得:
,
整理得:,
解得:,(不合题意,舍去)
当时,,符合题意.
答:五月份的销售单价应是80元.
【点睛】本题主要考查了一元二次方程的应用,明确题意,准确得到等量关系是解题的关键.
15.200元/张
【分析】可设票价应定为x元,根据票价×销售的票数=获得门票收入,即可列出一元二次方程,解之即可,再根据让利于民进行取舍.
【详解】解:设票价应定为x元/张,依题意有
,
解得:,.
∵要让利于民,
∴,
答:票价应定为200元/张.
【点睛】此题考查一元二次方程的实际运用,找出销售问题中的基本数量关系是解决问题的关键.
16.(1)190,
(2)50人
(3)
【分析】(1)利用通话总次数本班人数(本班人数),即可得出结论;
(2)根据同学们共通话1225次,即可得出关于n的一元二次方程,解之取其正值即可得出结论;
(3)利用线段的总数点的个数(点的个数),即可用含m的代数式表示出线段的总数.
【详解】(1)解:根据题意得:若本班人数为20,则共通话次,
若本班人数为,则共通话;
故答案为:190,
(2)解:由题意得:,
∴,
解得:,(不合题意,舍去),
答:该班同学的人数为50人.
(3)解:线段上共有个点(包含端点、),则相当于通话人数为,
所以线段总数为(条)
【点睛】本题考查了一元二次方程的应用以及列代数式,解题的关键是:(1)根据各数量之间的关系,用含n的代数式表示出通话总数;(2)找准等量关系,正确列出一元二次方程;(3)根据各数量之间的关系,用含m的代数式表示出线段总数.
17.(1)40;1800
(2)商场每天要盈利2100元,每台空气加湿器应降价20元
【分析】(1)根据题意列出有算式,进行计算即可求解;
(2)设每台空气加湿器应降价元,根据题意列出一元一次方程,解方程即可求解.
【详解】(1)解: (台),
(元).
故答案为:40;1800.
(2)设每台空气加湿器应降价元,
则每台盈利元,每天可以售出台,
依题意得:,
整理的:,
解得:,,
在尽快减少库存的前提下,
的值为20,
在尽快减少库存的前提下,商场每天要盈利2100元,每台空气加湿器应降价20元.
【点睛】本题考查了一元二次方程的应用,根据题意列出方程是解题的关键.
18.(1)小拉伊卜玩偶售价为元,大拉伊卜玩偶售价是元
(2)
【分析】(1)设小拉伊卜售价为x元,则大拉伊卜售价是元,根据题意,得,解分式方程即可.
(2)根据题意,第二周大拉伊卜售价是元,销售数量为个;第二周小拉伊卜售价是元,销售数量为个,根据题意,得,解方程即可.
【详解】(1)解:设小拉伊卜售价为x元,则大拉伊卜售价是元,
根据题意,得,
解得,
经检验,是原方程的根,
所以,
答:小拉伊卜玩偶售价为元,大拉伊卜玩偶售价是元.
(2)解:根据题意,第二周大拉伊卜售价是元,销售数量为个;第二周小拉伊卜售价是元,销售数量为个,
根据题意,得,
解得(舍去).
故的值为.
【点睛】本题考查了分式方程的应用,一元二次方程的应用,熟练掌握两种的方程的应用是解题的关键.
19.(1)的值为负
(2)等边三角形
【分析】(1)运用因式分解法将转化为,借助三角形的三边关系问题即可解决;
(2)运用配方法,将所给等式的左边变形、配方,利用非负数的性质问题即可解决.
【详解】(1)解:,
的三条边分别是,
,
的值的为负;
(2)解:,
,
即,
又,,
,
为等边三角形.
【点睛】本题主要考查了因式分解、配方法在代数式的化简求值、几何图形形状的判断等方面的应用问题,解题的关键是灵活运用,正确变形,准确判断.
20.(1)
(2)不可能,见解析
【分析】(1)根据三角形的面积公式可以得出面积为:,的面积为,由题意列出方程解答即可;
(2)由等量关系列方程求出t的值,但方程无解,从而可得答案.
【详解】(1)解:由题意知,,,
∴,,
∴,
整理得,解得,
答:当时的面积为面积的;
(2)不能,理由如下:
当时,
,
整理得,
∵△,
∴此方程没有实数根,
∴的面积不可能是面积的一半.
【点睛】本题考查了一元二次方程的应用,三角形的面积,解题的关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十一章一元二次方程解答题专项特训-数学九年级上册人教版
1.阅读下面的例题,解方程的过程如下:
①当时,原方程化为,解得:(舍去).
②当时,原方程可化为,解得:(舍去).
原方程的解:.
请参照例题解方程:.
2.已知关于的一元二次方程有两个实数根.
(1)求的取值范围;
(2)如果方程的两个实数根为,且,求的值.
3.如图,在矩形中,点是的中点,,,动点P从点A出发,以3cm/s的速度向点B运动,到达点B时停止运动;动点Q同时从点C出发,以2cm/s的速度向点D运动.设运动的时间为t s.
(1)当______s时,以为顶点的四边形是平行四边形;
(2)当t为何值时,点P和点Q之间的距离为10cm.
4.阅读材料,回答下列问题:
反序数:
有这样一对数,一个数的数字排列完全颠倒过来变成另一个数,简单的说,就是顺序相反的两个数,我们把这样的一对数称为“反序数”,比如:的反序数是,的反序数是.
用方程知识解决问题:
若一个两位数,其十位上的数字比个位上的数字大3,这个两位数与其反序数之积为,求这个两位数.
5.如图,有一段长为20米的篱笆,利用一面墙,围成一个长方形花圃,设花圃的宽AB为x米(其中.
(1)请你用含x的代数式表示BC的长.
(2)若此时花圃的面积刚好为,求此时花圃的宽AB的长度.
6.古算趣题:“笨伯执竿要进屋,无奈门框拦住竹,横多四尺竖多二,没法急得放声哭,有个邻居聪明者,教他斜竿对两角,笨伯依言试一试,不多不少刚抵足,借问竿长多少数,谁人算出我佩服”.其大意是:笨伯拿竹竿进屋,横拿竖拿都进不去,横着比门宽4尺,竖着比门高2尺.他的邻居教他沿着门的对角线斜着拿竿,笨伯一试,刚好进去.问:竹竿有多少尺?
7.如图,要把长为、宽为的长方形花坛四周扩展相同的宽度,得到面积为的新长方形花坛,求扩展的宽度.
8.(换元法)解方程:
解:设则原方程可化为
解得:
当时,,解得
当时,,解得
∴原方程的根是,
根据以上材料,请解方程:
(1).
(2)
9.某超市以每千克40元的价格购进菠萝蜜,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种菠萝蜜销售量y(千克)与每千克降价x(元)()之间满足一次函数关系,其图像如图所示.
(1)求y与x之间的函数关系式.
(2)当每千克菠萝蜜降价4元时,超市获利多少元?
(3)若超市要想获利2400元,且让顾客获得更大实惠,这种菠萝蜜每千克应降价多少元?
10.阅读材料,解答问题.
阅读材料:
为解方程,我们可以将视为一个整体;然后设,则,原方程化为.①
解得,.
当时,,,,
当时,,,.
原方程的解为,,,.
解答问题:
(1)填空在由原方程得到方程①的过程中,利用________法达到了降次的目的;体现了________的数学思想.
(2)解方程.
11.如图,已知等腰三角形,,,点从点出发,沿的方向以的速度向终点运动,同时点从点出发,沿的方向以的速度向终点运动,当点运动到点时,两点均停止运动,运动时间记为秒,请解决下列问题:
(1)若点在边上,当为何值时,?
(2)是否存在这样的值,使的面积为?若存在,请求出的值,若不存在,请说明理由.
12.某超市销售一种商品,每件盈利50元,平均每天可达到30件.为尽快减少库存,现在准备降价促销.经调查发现:一件商品降价1元平均每天可以多销售2件.
(1)当一件商品降价5元时,每天的销售量可达到_____________件,每天共盈利_______________元;
(2)在上述条件不变、销售正常的情况下,每件商品降价多少元该超市每天的盈利为2100元,同时也更加优惠?
13.由于疫情反弹,某地区开展了连续全员核酸检测,9月7日,医院派出13名医护人员到一个大型小区设置了、两个采样点进行核酸采样,当天共采样9220份,已知点平均每人采样720份,点平均每人采样700份.
(1)求、两点各有多少名医护人员?
(2)9月8日,医院继续派出这13名医护人员前往这个小区进行核酸采样,这天,社区组织者将附近数个商户也纳入这个小区采样范围,同时重新规划,决定从点抽调部分医护人员到点经调查发现,点每减少1名医护人员,人均采样量增加10份,点人均采样量不变,最后当天共采样9360份,求从点抽调了多少名医护人员到点?
14.六一节前某市场以每盒60元的价格购进1000盒拼装玩具.四月份以单价100元销售,售出了300盒.五月份如果销售单价不变,预计仍可售出300盒,市场为增加销售量,决定降价销售,根据市场调查,销售单价每降低3元,可多售出6盒,但最低销售单价应高于购进的价格.五月份结束后,批发商将对剩余的玩具一次性清仓,清仓时销售单价为50元.设五月份销售单价降低x元.
(1)填空:五月销售量为______件,清仓销售量为______件.
(2)如果市场希望通过销售这批玩具获利15200元,那么五月份的销售单价应是多少元?
15.某演出团体准备在常州大剧院举办迎新演出,该剧院共有1500个座位.如果票价定为每张100元,那么门票可以全部售出;如果票价每增加1元/张,那么门票就会减少3张.演出团体既要让利于民又要使得门票收入为240000元,则票价应该定为多少元/张?
16.新年到了,为增进同学友谊,某班主任规定本班同学间,每两个人必须相互通电话1次
(1)若本班人数为20,则共通话________次,若本班人数为(,且为正整数),则共通话________次;
(2)若同学们共通话1225次,求该班同学的人数;
(3)王峰同学由打电话问题想到了一个数学问题:若线段上共有个点(不含端点、),线段总数为多少呢?请直接写出结论.
17.某商场销售一批空气加湿器,平均每天可售出30台,每台可盈利50元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每台降价1元,商场平均每天可多售出2台.
(1)若该商场某天降价了5元,则当天可售出 台,当天共盈利 元;
(2)在尽快减少库存的前提下,商场每天要盈利2100元,每台空气加湿器应降价多少元?
18.年卡塔尔世界杯吉祥物,中文名是拉伊卜,代表着技艺高超的球员.随着世界杯的火热进行,吉祥物拉伊卜玩偶成为畅销商品.某经销商售卖大、小两种拉伊卜玩偶,大拉伊卜售价是小拉伊卜售价的倍且元购买小拉伊卜玩偶的数量比购买大拉伊卜玩偶的数量多个.
(1)求小、大拉伊卜玩偶售价分别为多少元?
(2)世界杯开赛第一周该经销商售出小拉伊卜玩偶个,大拉伊卜玩偶个,世界杯开赛第二周,该经销商决定降价出售两种拉伊卜玩偶.已知:两种拉伊卜玩偶都降价元,小拉伊卜玩偶售出数量较世界杯开赛第一周多了个:大拉伊卜玩偶售出数量与世界杯开赛第一周相同,该经销商世界杯第二周总销售额为元,求的值.
19.已知的三条边分别是.
(1)判断的值的正负.
(2)若满足,判断的形状.
20.如图,中,,,,一动点P从点C出发沿着方向以的速度运动,另一动点Q从A出发沿着边以的速度运动,P,Q两点同时出发,运动时间为.
(1)若的面积是面积的,求t的值?
(2)的面积能否为面积的一半?若能,求出t的值;若不能,说明理由.
参考答案:
1.
【分析】分和,两种情况进行讨论求解即可.
【详解】解:当时,原方程化为,解得:(舍去).
当时,原方程可化为,解得:(舍去).
原方程的解:.
【点睛】本题考查解一元二次方程.理解并掌握题干中给出的解方程的方法,是解题的关键.
2.(1)
(2)
【分析】(1)根据一元二次方程根的判别式进行求解即可;
(2)根据一元二次方程根与系数的关系得到,,再由完全平方公式的变形得到,由此解方程即可得到答案.
【详解】(1)解:根据题意,得,即,
∴;
(2)解:由根与系数的关系,得,,
∵,
∴,即,
解得(舍去), .
∴的值为.
【点睛】本题主要考查了一元二次方程根的判别式,根与系数的关系,解一元二次方程,完全平方公式的变形求值,灵活运用所学知识是解题的关键.
3.(1)
(2)或
【分析】(1)利用平行四边形的性质得出当时,四边形为平行四边形求出即可;
(2)设当秒时cm,利用勾股定理得出即可;
【详解】(1)解:如图,
当四边形为平行四边形时,则,
,
解得
当s时,以为顶点的四边形是平行四边形;
(2)解:设运动时间为s,由题意得,.
①如图1,当点P在点Q的上方时,过点P作于点M.
在中,,,,
由勾股定理得,即,解得.
②如图2,当点P在点Q的下方时,过点P作于点N.
在中,,,.
由勾股定理得,即,解得.
由得符合题意.
综上得或.
【点睛】本题主要考查了平行四边形的性质及勾股定理和一元二次方程的应用等知识,熟练应用平行四边形的性质是解题关键.
4.
【分析】设这个两位数的个位数字为x,则十位数字为,根据这个两位数与其反序数之积为,可得出关于x的一元二次方程,解之取其符合题意的值,即可得出结论.
【详解】解:设这个两位数的个位数字为x,则十位数字为,
根据题意得:,
∴,即,
∴,
∴
解得或(舍去),
∴,
∴这个两位数为.
【点睛】本题主要考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
5.(1)
(2)3
【分析】(1)根据题意,求解即可;
(2)根据题意,列出一元二次方程,求解即可.
【详解】(1)解:∵篱笆的全长为20米,花圃的宽AB为x米,
的长为米;
(2)解:根据题意得:,
整理得:,
解得:,,
当时,,符合题意;
当时,,不符合题意,舍去.
答:此时花圃的宽AB的长度是3米.
【点睛】此题考查了一元二次方程的应用,解题的关键是理解题意,找到等量关系,正确列出方程.
6.10尺
【分析】设竹竿的长为尺,根据横着比门宽4尺,竖着比门高2尺,得到两条直角边长分别为尺和尺,根据沿对角线斜着拿竿,笨伯一试,刚好进去得到直角三角形斜边为尺,根据勾股定理列方程,解方程即可.
【详解】解:设竹竿的长为尺,根据题意,得
.
解这个方程,得,.
当时,,,不符合题意,舍去,
.
答:竹竿的长为10尺.
【点睛】此题考查了勾股定理和一元二次方程的应用,读懂题意,根据勾股定理列出一元二次方程是解题的关键.
7.扩展的宽度为
【分析】利用长方形的面积计算公式,结合新长方形花坛的面积为,即可得出关于的一元二次方程,解之取其正值即可得出结论.
【详解】解:设扩展的宽度为,
依题意,得:,
整理得:,
解得:,(不合题意,舍去).
答:扩展的宽度为.
【点睛】本题考查了一元二次方程的应用.找准等量关系,正确列出一元二次方程是解题的关键.
8.(1)原方程的根是;
(2)原方程的根是.
【分析】(1)设,则原方程可化为,解得的值,即可得到原方程的根;
(2)设,则原方程可化为,解得的值,检验后即可得到原方程的根.
【详解】(1)设,则原方程可化为
解得∶
当时,,解得
当时,,方程无解
原方程的根是;
(2)设,则原方程可化为
去分母,可得
解得
当时,,解得
当时,,方程无解
经检验∶都是原方程的解
原方程的根是.
【点睛】本题主要考查了运用换元法解一元二次方程以及分式方程,解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法.
9.(1)
(2)2240元
(3)12元
【分析】(1)运用待定系数法求解即可.
(2)先计算每千克菠萝蜜的利润,乘以销售量即可.
(3)列方程求解,且取较大值.
【详解】(1)设y与x之间的函数关系式为,
将,代入,
得,
解得,
∴y与x之间的函数关系式为.
(2)(元).
答:当每千克菠萝蜜降价4元时,超市获利2240元.
(3)依题意,得,
整理,得,
解得,.
∵要让顾客获得更大实惠,∴.
答:这种菠萝蜜每千克应降价12元.
【点睛】本题考查了一次函数的解析式及其应用,一元二次方程的解法,熟练掌握待定系数法,解方程是解题的关键.
10.(1)换元,转化
(2)
【分析】(1)题目中的方法用的是换元法,体现了转化的数学思想;
(2)令,得,用因式分解法解方程求出a的值,再求出x的值.
【详解】(1)解:在由原方程得到方程①的过程中,利用换元法达到了降幂的目的,体现了转化的数学思想,
故答案为:换元,转化;
(2)解:令,则原方程变为,
∴,
解得或,
∵,
∴,
∴,
∴.
【点睛】本题考查用换元法解一元二次方程,解题的关键是掌握换元法解一元二次方程的方法.
11.(1),当时
(2)存在;当或时,的面积为
【分析】(1)先根据已知条件求出的长度,再设经过 秒,是直角三角形,此时, ,当,,解方程即可;
(2)设经过秒,的面积为,连接,作于,分类讨论点在边上和点在边上,,即可求解.
【详解】(1)解:过点作,如图所示:
∵等腰三角形,,,
∴,
∴,
∴,
设经过秒,是直角三角形,则
, ,
当时,如图所示:
∴,
∴,
解得:,
若点在边上,当时
(2)存在,理由如下:
当点在边上,连接,过点作于,如图所示:
设经过秒,的面积为,则
, ,
∴,
∴,
∴,
解得:,(舍),
当点在边上,连接,,作于,如图所示:
设经过秒,的面积为,则
,,
∴,
∴,
∴,
解得:,(舍去),
∴当或时,的面积为.
【点睛】本题考查了一元二次方程、一元一次方程的应用和三角形与动点问题的综合,分类讨论思想和数形结合的思想是解决本题的关键.
12.(1),
(2)销售正常情况下,每件商品降价20元时超市每天盈利可达到2100元,同时也更加优惠.
【分析】(1)根据“一件商品每降价1元平均每天可多售出2件”即可求出每天销售量,根据销售量乘以每件盈利即可得到每天共盈利的钱数;
(2)设每件商品降价x元时超市每天盈利可达到2100元,根据销售量乘以每件盈利即可得到每天共盈利总数,列出方程求解即可.
【详解】(1)解:当一件商品降价5元时,每天销售量可达到(件),
每天共盈利(元),
故答案为:,;
(2)解:设每件商品降价元时超市每天盈利可达到元,
由题意得,,
解得,
根据题意,符合题意,
答:销售正常情况下,每件商品降价元时超市每天盈利可达到元,同时也更加优惠.
【点睛】此题考查了一元二次方程的应用,读懂题意,正确列出方程是解题的关键.
13.(1)A检测队有6人,B检测队有7人
(2)从B检测队中抽调了2人到A检测队
【分析】(1)设A点有x名医护人员,B点有y名医护人员,根据“A、B两个采样点共13名医护人员,且当天共采样9220份”,即可得出关于x,y的且当天共采样9220份,即可得出关于x, y的二元一次方程组,解之即可得出结论;
(2)设从B点抽调了m名医护人员到A点,则B点平均每人采样份,根据重新规划后当天共采样9360份,即可得出关于m的一元_二次方程,解之取其符合题意的值,即可得出结论.
【详解】(1)解:设A检测队有人,B检测队有人,
依题意得:,分解得:
答:A检测队有6人,B检测队有7人;
(2)解:设从B检测队中抽调了人到A检测队,则B检测队人均采样人,
依题意得:,
解得:,解得:,,
由于从B对抽调部分人到A检测队,则故,
答:从B检测队中抽调了2人到A检测队.
【点睛】本题考查了二元一次方程组的应用以及一元二次方程的应用,解题的关键是:(1)找准等关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元二次方程.
14.(1),
(2)五月份的销售单价应是80元
【分析】(1)设五月份销售单价降低x元,则十月份销售单价为元,再根据销售单价每降低3元,可多售出6盒求出五月份的销售量即可求出清仓销售的数量;
(2)根据“销售这批玩具获利15200元”,列出方程,即可求解.
【详解】(1)解:设五月份销售单价降低x元,则
五月份销售单价为元, 销售量为件,
五月份结束后,剩余的玩具的数量为件,
故答案为:,
(2)解:依题意得:
,
整理得:,
解得:,(不合题意,舍去)
当时,,符合题意.
答:五月份的销售单价应是80元.
【点睛】本题主要考查了一元二次方程的应用,明确题意,准确得到等量关系是解题的关键.
15.200元/张
【分析】可设票价应定为x元,根据票价×销售的票数=获得门票收入,即可列出一元二次方程,解之即可,再根据让利于民进行取舍.
【详解】解:设票价应定为x元/张,依题意有
,
解得:,.
∵要让利于民,
∴,
答:票价应定为200元/张.
【点睛】此题考查一元二次方程的实际运用,找出销售问题中的基本数量关系是解决问题的关键.
16.(1)190,
(2)50人
(3)
【分析】(1)利用通话总次数本班人数(本班人数),即可得出结论;
(2)根据同学们共通话1225次,即可得出关于n的一元二次方程,解之取其正值即可得出结论;
(3)利用线段的总数点的个数(点的个数),即可用含m的代数式表示出线段的总数.
【详解】(1)解:根据题意得:若本班人数为20,则共通话次,
若本班人数为,则共通话;
故答案为:190,
(2)解:由题意得:,
∴,
解得:,(不合题意,舍去),
答:该班同学的人数为50人.
(3)解:线段上共有个点(包含端点、),则相当于通话人数为,
所以线段总数为(条)
【点睛】本题考查了一元二次方程的应用以及列代数式,解题的关键是:(1)根据各数量之间的关系,用含n的代数式表示出通话总数;(2)找准等量关系,正确列出一元二次方程;(3)根据各数量之间的关系,用含m的代数式表示出线段总数.
17.(1)40;1800
(2)商场每天要盈利2100元,每台空气加湿器应降价20元
【分析】(1)根据题意列出有算式,进行计算即可求解;
(2)设每台空气加湿器应降价元,根据题意列出一元一次方程,解方程即可求解.
【详解】(1)解: (台),
(元).
故答案为:40;1800.
(2)设每台空气加湿器应降价元,
则每台盈利元,每天可以售出台,
依题意得:,
整理的:,
解得:,,
在尽快减少库存的前提下,
的值为20,
在尽快减少库存的前提下,商场每天要盈利2100元,每台空气加湿器应降价20元.
【点睛】本题考查了一元二次方程的应用,根据题意列出方程是解题的关键.
18.(1)小拉伊卜玩偶售价为元,大拉伊卜玩偶售价是元
(2)
【分析】(1)设小拉伊卜售价为x元,则大拉伊卜售价是元,根据题意,得,解分式方程即可.
(2)根据题意,第二周大拉伊卜售价是元,销售数量为个;第二周小拉伊卜售价是元,销售数量为个,根据题意,得,解方程即可.
【详解】(1)解:设小拉伊卜售价为x元,则大拉伊卜售价是元,
根据题意,得,
解得,
经检验,是原方程的根,
所以,
答:小拉伊卜玩偶售价为元,大拉伊卜玩偶售价是元.
(2)解:根据题意,第二周大拉伊卜售价是元,销售数量为个;第二周小拉伊卜售价是元,销售数量为个,
根据题意,得,
解得(舍去).
故的值为.
【点睛】本题考查了分式方程的应用,一元二次方程的应用,熟练掌握两种的方程的应用是解题的关键.
19.(1)的值为负
(2)等边三角形
【分析】(1)运用因式分解法将转化为,借助三角形的三边关系问题即可解决;
(2)运用配方法,将所给等式的左边变形、配方,利用非负数的性质问题即可解决.
【详解】(1)解:,
的三条边分别是,
,
的值的为负;
(2)解:,
,
即,
又,,
,
为等边三角形.
【点睛】本题主要考查了因式分解、配方法在代数式的化简求值、几何图形形状的判断等方面的应用问题,解题的关键是灵活运用,正确变形,准确判断.
20.(1)
(2)不可能,见解析
【分析】(1)根据三角形的面积公式可以得出面积为:,的面积为,由题意列出方程解答即可;
(2)由等量关系列方程求出t的值,但方程无解,从而可得答案.
【详解】(1)解:由题意知,,,
∴,,
∴,
整理得,解得,
答:当时的面积为面积的;
(2)不能,理由如下:
当时,
,
整理得,
∵△,
∴此方程没有实数根,
∴的面积不可能是面积的一半.
【点睛】本题考查了一元二次方程的应用,三角形的面积,解题的关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
