二次函数复习
图片预览





文档简介
课件26张PPT。二 次 函 数
新课标知识结构概念理解经典考题第一课时义务教育课程标准实验区中考总复习 高新区镇湖中学 花修平返回
通过对实际问题情境的分析确定二次会用描点法画二次函数的图象,能从图象上认识二次函数的性质。会根据公式确定图象的顶点、开口方向和对称轴(公式不要求推导和记忆),并能解决简单的实际问题。会利用二次函数的图象求一元二次、二元一次方程组的近似值。函数的表达式,体会二次函数的意义新课标内容解读返回
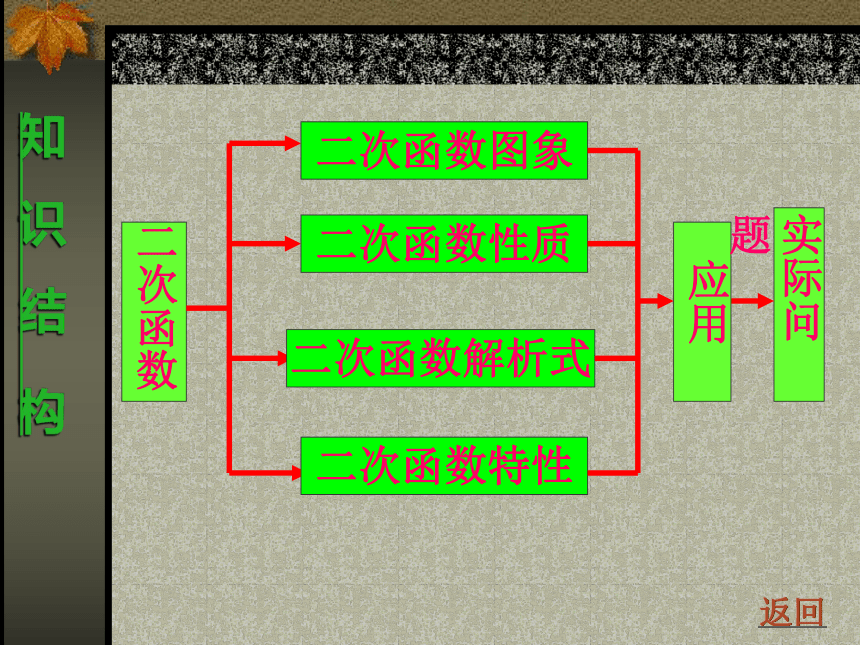
二次函数二次函数图象二次函数性质二次函数特性二次函数解析式应用实际问题知 识 结 构返回
知 识 点 总 结二、图象一、概念三、性质四解析式返回
知 识 点 总 结一般地,如果 y=ax2+bx+c(a,b,c 是常数,a≠0),那么,y叫做x的二次函数。返回
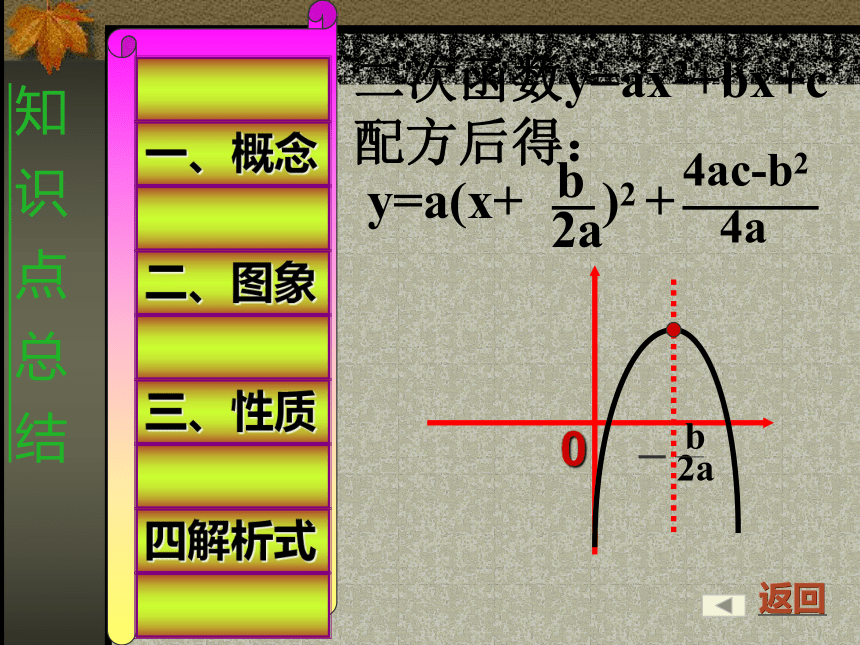
知 识 点 总 结二、图象一、概念三、性质四解析式0二次函数的图象及性质当a>0时开口向上,并向上无限延伸;
当a<0时开口向下,并向下无限延伸.(0,0)(0,c)(h,0)(h,k)y轴在对称轴左侧,y随x的增大而减小在对称轴右侧,y随x的增大而增大在对称轴左侧,y随x的增大而增大在对称轴右侧,y随x的增大而减小y轴返回
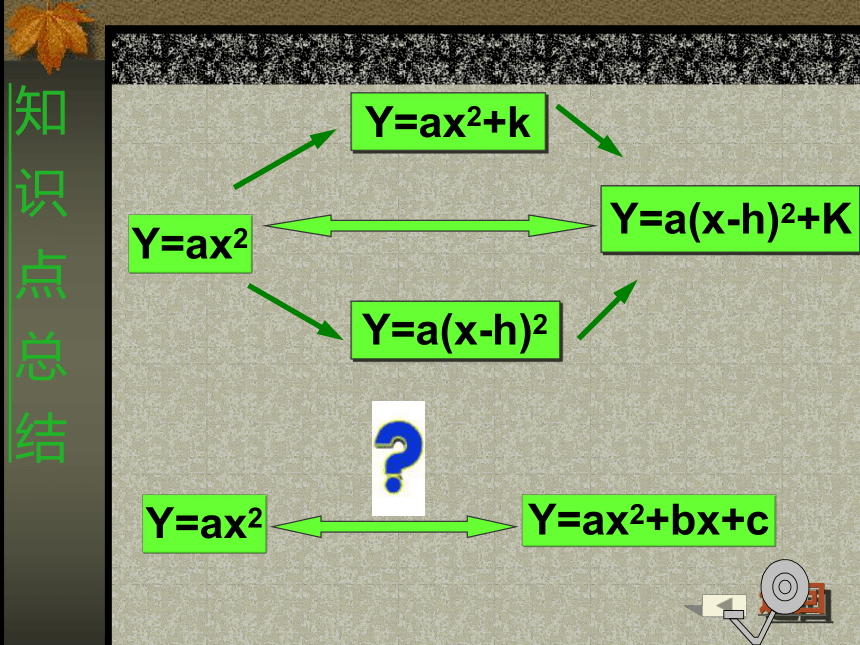
知 识 点 总 结二、图象一、概念三、性质四解析式y=a(x-h)2+ky=ax2+bx+c
y=a(x-x1)
(x-x2)返回
知 识 点 总 结Y=ax2Y=ax2+kY=a(x-h)2Y=a(x-h)2+KY=ax2Y=ax2+bx+c 解:由题意知:解得:m=-2练习1:函数y=(m+1)xm2-m+mx-1 是二次函数,则m= 。经 典 例 题 解 析X的最高次数是2二次项系数a≠0经 典 例 题 解 析 已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两
点,求C, A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,
y有最大 (小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?经 典 例 题 解 析解:经 典 例 题 解 析解0xy?(-3,0)(1,0)3经 典 例 题 解 析解0?M(-1,-2)??C(0,-–)??A(-3,0)B(1,0)3 2yxD经 典 例 题 解 析解0xx=-1??(0,-–)??(-3,0)(1,0)3 2:(5)?(-1,-2)当x=-1时,y有最小值为
y最小值=-2
当x≤-1时,y随x的增大
而减小;经 典 例 题 解 析解:0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2yx(6) 当x< -3或x>1时,y > 0返回经 典 例 题 解 析经 典 例 题 解 析根据下列条件求二次函数解析式:你用了什么方法?你的方法简单吗? 小 结 :
能够从题目条件中总结
二次函数的特征,采用
适当的二次函数的解析
式形式,使问题简单化。本节小结课外作业1、请大家完成练习卷;2、请大家完成《能力 自测》的相关内容。再 见
执教 : 镇湖中学 花修平祝各位领导、同仁身体健康,工作顺利!
同学们辛苦了!返回练习2
(1)填写表中的空格:练 习 巩 固经 典 例 题 解 析xy0练习:把抛物线y=x2通过怎样平移能得到抛物线y=x2-2x+3?
二、二次函数的图象及性质二次函数y=ax2+bx+c(a≠0)的图象是抛物线.
当a>0时开口向上,并向上无限延伸;
当a<0时开口向下,并向下无限延伸.知 识 点 总 结练 习 巩 固练习2你能快速画出它的示意图吗?
①画对称轴
②确定顶点
③确定与坐
标轴交点
④ 连 线
新课标知识结构概念理解经典考题第一课时义务教育课程标准实验区中考总复习 高新区镇湖中学 花修平返回
通过对实际问题情境的分析确定二次会用描点法画二次函数的图象,能从图象上认识二次函数的性质。会根据公式确定图象的顶点、开口方向和对称轴(公式不要求推导和记忆),并能解决简单的实际问题。会利用二次函数的图象求一元二次、二元一次方程组的近似值。函数的表达式,体会二次函数的意义新课标内容解读返回
二次函数二次函数图象二次函数性质二次函数特性二次函数解析式应用实际问题知 识 结 构返回
知 识 点 总 结二、图象一、概念三、性质四解析式返回
知 识 点 总 结一般地,如果 y=ax2+bx+c(a,b,c 是常数,a≠0),那么,y叫做x的二次函数。返回
知 识 点 总 结二、图象一、概念三、性质四解析式0二次函数的图象及性质当a>0时开口向上,并向上无限延伸;
当a<0时开口向下,并向下无限延伸.(0,0)(0,c)(h,0)(h,k)y轴在对称轴左侧,y随x的增大而减小在对称轴右侧,y随x的增大而增大在对称轴左侧,y随x的增大而增大在对称轴右侧,y随x的增大而减小y轴返回
知 识 点 总 结二、图象一、概念三、性质四解析式y=a(x-h)2+ky=ax2+bx+c
y=a(x-x1)
(x-x2)返回
知 识 点 总 结Y=ax2Y=ax2+kY=a(x-h)2Y=a(x-h)2+KY=ax2Y=ax2+bx+c 解:由题意知:解得:m=-2练习1:函数y=(m+1)xm2-m+mx-1 是二次函数,则m= 。经 典 例 题 解 析X的最高次数是2二次项系数a≠0经 典 例 题 解 析 已知二次函数y=—x2+x-—
(1)求抛物线开口方向,对称轴和顶点M的坐标。
(2)设抛物线与y轴交于C点,与x轴交于A、B两
点,求C, A,B的坐标。
(3)画出函数图象的示意图。
(4)求ΔMAB的周长及面积。
(5)x为何值时,y随的增大而减小,x为何值时,
y有最大 (小)值,这个最大(小)值是多少?
(6)x为何值时,y<0?x为何值时,y>0?经 典 例 题 解 析解:经 典 例 题 解 析解0xy?(-3,0)(1,0)3经 典 例 题 解 析解0?M(-1,-2)??C(0,-–)??A(-3,0)B(1,0)3 2yxD经 典 例 题 解 析解0xx=-1??(0,-–)??(-3,0)(1,0)3 2:(5)?(-1,-2)当x=-1时,y有最小值为
y最小值=-2
当x≤-1时,y随x的增大
而减小;经 典 例 题 解 析解:0?(-1,-2)??(0,-–)??(-3,0)(1,0)3 2yx(6) 当x< -3或x>1时,y > 0返回经 典 例 题 解 析经 典 例 题 解 析根据下列条件求二次函数解析式:你用了什么方法?你的方法简单吗? 小 结 :
能够从题目条件中总结
二次函数的特征,采用
适当的二次函数的解析
式形式,使问题简单化。本节小结课外作业1、请大家完成练习卷;2、请大家完成《能力 自测》的相关内容。再 见
执教 : 镇湖中学 花修平祝各位领导、同仁身体健康,工作顺利!
同学们辛苦了!返回练习2
(1)填写表中的空格:练 习 巩 固经 典 例 题 解 析xy0练习:把抛物线y=x2通过怎样平移能得到抛物线y=x2-2x+3?
二、二次函数的图象及性质二次函数y=ax2+bx+c(a≠0)的图象是抛物线.
当a>0时开口向上,并向上无限延伸;
当a<0时开口向下,并向下无限延伸.知 识 点 总 结练 习 巩 固练习2你能快速画出它的示意图吗?
①画对称轴
②确定顶点
③确定与坐
标轴交点
④ 连 线
