第二十二章二次函数单元试卷(无答案) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章二次函数单元试卷(无答案) 2023—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 307.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 23:04:12 | ||
图片预览

文档简介
2023-2024学年人教版数学九上第二十二章二次函数单元试卷
一、选择题
1.下列函数表达式中,一定为二次函数的是( )
A. B. C. D.
2.二次函数的图象与轴的交点个数是( )
A.0个 B.1个 C.2个 D.3个
3.如果抛物线经过点,,则这条抛物线的对称轴为( )
A.轴 B.直线 C.直线 D.直线
4.抛物线y=(x―1)2-9经变换后得到抛物线y=x2+2x-8,则下列变换正确的是( )
A.向左平移6个单位长度 B.向右平移6个单位长度
C.向左平移2个单位长度 D.向右平移2个单位长度
5.如图是抛物线形拱桥,当拱顶高离水面 时,水面宽 ,若水面上升 ,则水面宽为
A. B. C. D.
6.如图,在平面直角坐标系中,过点A且与x轴平行的直线交抛物线y=(x+1)2于B,C两点,若线段BC的长为6,则点A的坐标为( )
A.(0,1) B.(0,4.5) C.(0,3) D.(0,6)
7.若点M(﹣1,y1),N(1,y2),P()都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y1<y2 D.2<y1<y3
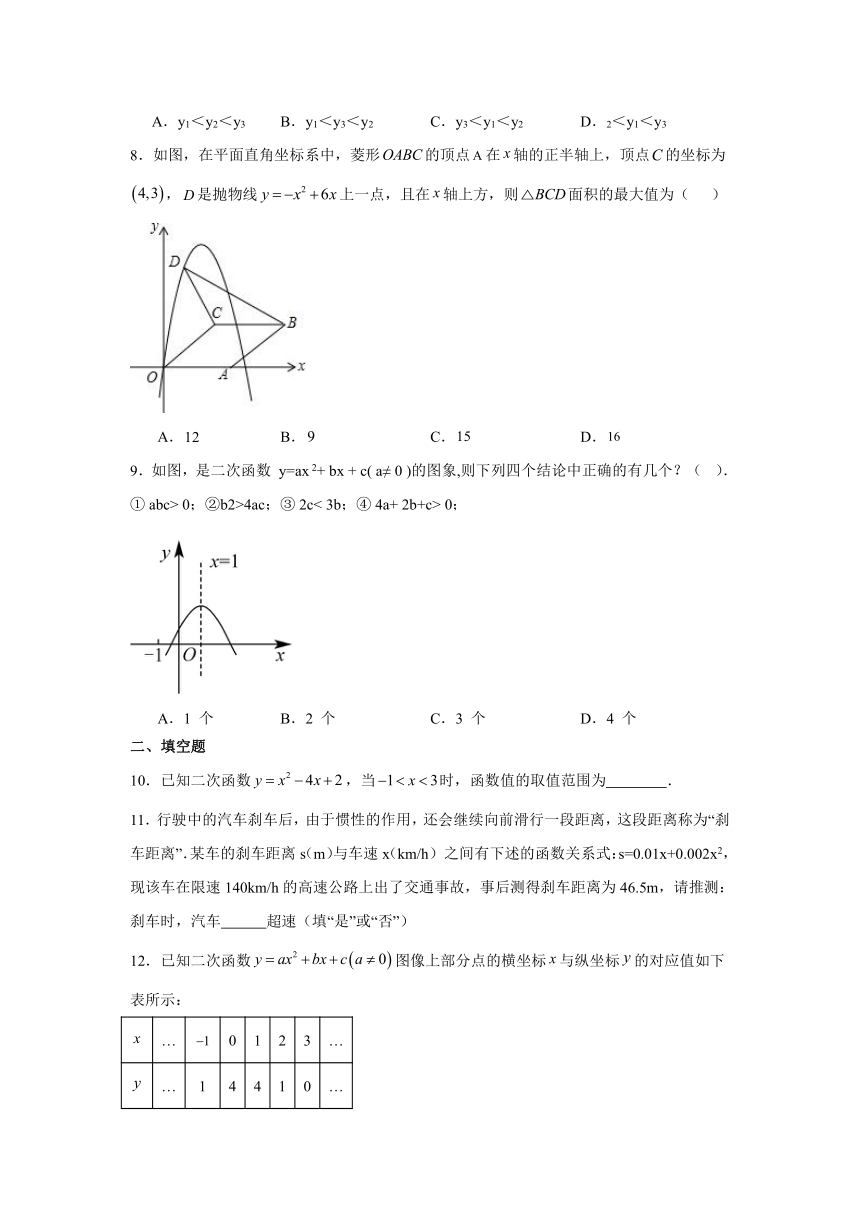
8.如图,在平面直角坐标系中,菱形的顶点在轴的正半轴上,顶点的坐标为,是抛物线上一点,且在轴上方,则面积的最大值为( )
A. B. C. D.
9.如图,是二次函数 y=ax 2+ bx + c( a≠ 0 )的图象,则下列四个结论中正确的有几个?( ).
① abc> 0;②b2>4ac;③ 2c< 3b;④ 4a+ 2b+c> 0;
A.1 个 B.2 个 C.3 个 D.4 个
二、填空题
10.已知二次函数,当时,函数值的取值范围为 .
11.行驶中的汽车刹车后,由于惯性的作用,还会继续向前滑行一段距离,这段距离称为“刹车距离”.某车的刹车距离s(m)与车速x(km/h)之间有下述的函数关系式:s=0.01x+0.002x2,现该车在限速140km/h的高速公路上出了交通事故,事后测得刹车距离为46.5m,请推测:刹车时,汽车 超速(填“是”或“否”)
12.已知二次函数图像上部分点的横坐标与纵坐标的对应值如下表所示:
… 0 1 2 3 …
… 1 4 4 1 0 …
那么它的图像的对称轴是直线 .
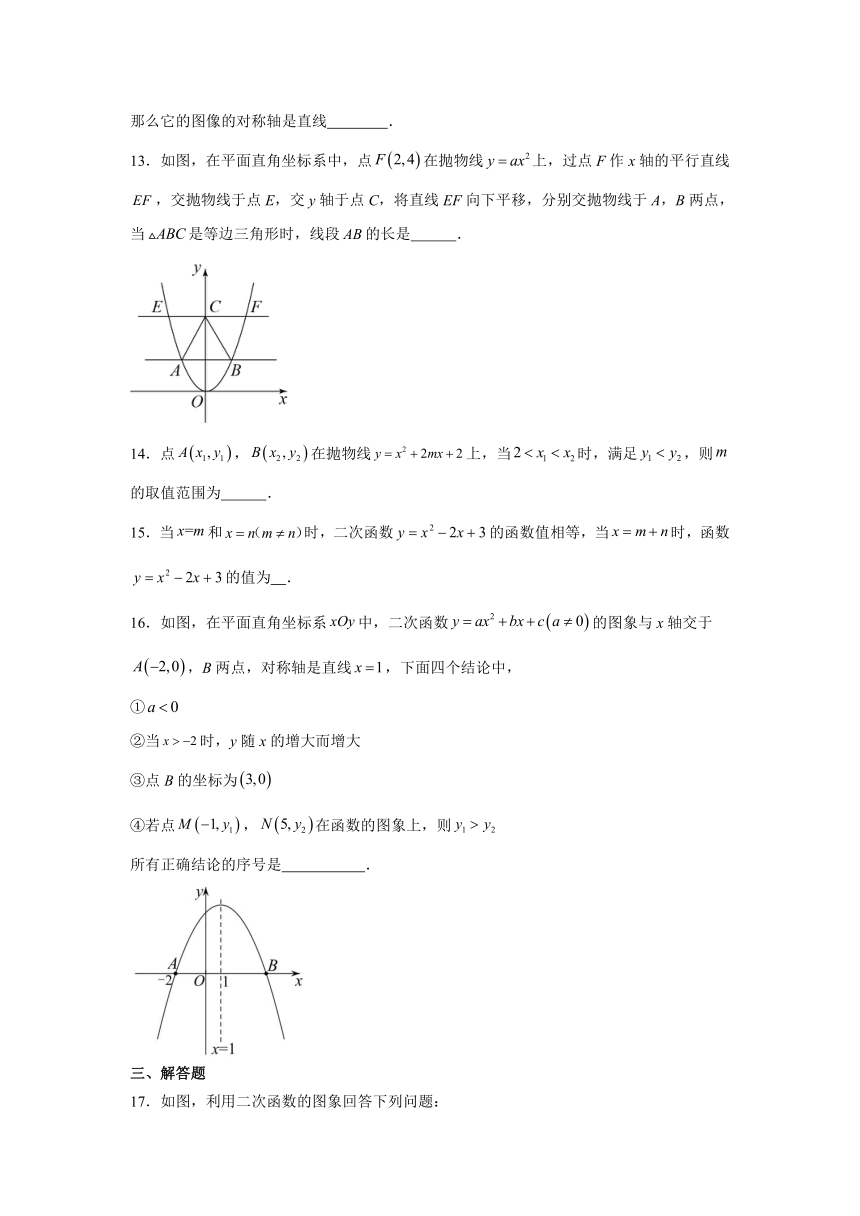
13.如图,在平面直角坐标系中,点在抛物线上,过点F作x轴的平行直线,交抛物线于点E,交y轴于点C,将直线EF向下平移,分别交抛物线于A,B两点,当是等边三角形时,线段的长是 .
14.点,在抛物线上,当时,满足,则的取值范围为 .
15.当和时,二次函数的函数值相等,当时,函数的值为 .
16.如图,在平面直角坐标系中,二次函数的图象与x轴交于,B两点,对称轴是直线,下面四个结论中,
①
②当时,y随x的增大而增大
③点B的坐标为
④若点,在函数的图象上,则
所有正确结论的序号是 .
三、解答题
17.如图,利用二次函数的图象回答下列问题:
(1)取什么值时,函数值大于0?
(2)取什么值时,函数值小于0?
(3)二次函数的最小值是多少?
(4)函数值随的增大是怎样变化的?
18.如图,抛物线y=﹣x2+bx+c与x轴相交于A(﹣3,0),D(1,0)两点,其中顶点为B.
(1)求该抛物线的解析式;
(2)若该抛物线与y轴的交点为C,求△ABC的面积.
19.为了践行“绿水青山就是金山银山”的发展理念,建设美丽成都,某小区计划在如图所示的一块长为8米,宽为6米的长方形空地上进行绿化,为了不影响人们的出行,需要在中间修建一条通道(图中阴影部分).设绿化所占面积为.
(1)求与的函数表达式;
(2)若要求,已知绿化的费用为每平方米元,修建通道的费用为每平方米40元,问如何设计可使总费用最低,最低费用为多少元?
20.如图,一次函数的图象与坐标轴交于点、,二次函数的图象过、两点.
(1)求二次函数的表达式;
(2)已知点在对称轴上,且点位于轴上方,连接,若,求点的坐标.
21.已知抛物线y=x2+kx+k﹣1.
(1)当k=3时,求抛物线与x轴的两个交点坐标;
(2)无论k取任何实数,抛物线过x轴上一定点,求定点坐标;
(3)当k=5时,设抛物线与y轴交于C点,与x轴交于A,B(点A在点B的左边)两点,连接AC,在线段AC上是否存在点D,使△ABD是直角三角形,若存在,求出点D的坐标,若不存在,请说明理由.
(4)点E(﹣1,1),点F(﹣2,2),抛物线与线段EF只有一个交点,求k的取值范围
22.国庆假期期间,某酒店有20个房间供游客居住,当每个房间每天的定价为100元时,房间恰好全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,酒店需对每个房间每天支出20元的各种费用,设每间房间定价x元().
(1)每天有游客居住的房间数为 (用含有x的式子表示);
(2)当每间房价为多少时,酒店当天的利润为1870元,且总支出最少?
(3)当每间房价定为多少元,酒店的利润W(元)最大,最大利润是多少?
23.如图1,在平面直角坐标系中,直线分别交轴、轴于,两点,经过,两点的抛物线与轴的正半轴相交于点,点为线段上的点,且点的横坐标为.
(1)求抛物线的解析式和直线的解析式;
(2)过作轴的平行线交抛物线于,当是为腰的等腰三角形时,求点的坐标;
(3)若顶点在以、为邻边的平行四边形的形内(不含边界),求m的取值范围.
一、选择题
1.下列函数表达式中,一定为二次函数的是( )
A. B. C. D.
2.二次函数的图象与轴的交点个数是( )
A.0个 B.1个 C.2个 D.3个
3.如果抛物线经过点,,则这条抛物线的对称轴为( )
A.轴 B.直线 C.直线 D.直线
4.抛物线y=(x―1)2-9经变换后得到抛物线y=x2+2x-8,则下列变换正确的是( )
A.向左平移6个单位长度 B.向右平移6个单位长度
C.向左平移2个单位长度 D.向右平移2个单位长度
5.如图是抛物线形拱桥,当拱顶高离水面 时,水面宽 ,若水面上升 ,则水面宽为
A. B. C. D.
6.如图,在平面直角坐标系中,过点A且与x轴平行的直线交抛物线y=(x+1)2于B,C两点,若线段BC的长为6,则点A的坐标为( )
A.(0,1) B.(0,4.5) C.(0,3) D.(0,6)
7.若点M(﹣1,y1),N(1,y2),P()都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y1<y2 D.2<y1<y3
8.如图,在平面直角坐标系中,菱形的顶点在轴的正半轴上,顶点的坐标为,是抛物线上一点,且在轴上方,则面积的最大值为( )
A. B. C. D.
9.如图,是二次函数 y=ax 2+ bx + c( a≠ 0 )的图象,则下列四个结论中正确的有几个?( ).
① abc> 0;②b2>4ac;③ 2c< 3b;④ 4a+ 2b+c> 0;
A.1 个 B.2 个 C.3 个 D.4 个
二、填空题
10.已知二次函数,当时,函数值的取值范围为 .
11.行驶中的汽车刹车后,由于惯性的作用,还会继续向前滑行一段距离,这段距离称为“刹车距离”.某车的刹车距离s(m)与车速x(km/h)之间有下述的函数关系式:s=0.01x+0.002x2,现该车在限速140km/h的高速公路上出了交通事故,事后测得刹车距离为46.5m,请推测:刹车时,汽车 超速(填“是”或“否”)
12.已知二次函数图像上部分点的横坐标与纵坐标的对应值如下表所示:
… 0 1 2 3 …
… 1 4 4 1 0 …
那么它的图像的对称轴是直线 .
13.如图,在平面直角坐标系中,点在抛物线上,过点F作x轴的平行直线,交抛物线于点E,交y轴于点C,将直线EF向下平移,分别交抛物线于A,B两点,当是等边三角形时,线段的长是 .
14.点,在抛物线上,当时,满足,则的取值范围为 .
15.当和时,二次函数的函数值相等,当时,函数的值为 .
16.如图,在平面直角坐标系中,二次函数的图象与x轴交于,B两点,对称轴是直线,下面四个结论中,
①
②当时,y随x的增大而增大
③点B的坐标为
④若点,在函数的图象上,则
所有正确结论的序号是 .
三、解答题
17.如图,利用二次函数的图象回答下列问题:
(1)取什么值时,函数值大于0?
(2)取什么值时,函数值小于0?
(3)二次函数的最小值是多少?
(4)函数值随的增大是怎样变化的?
18.如图,抛物线y=﹣x2+bx+c与x轴相交于A(﹣3,0),D(1,0)两点,其中顶点为B.
(1)求该抛物线的解析式;
(2)若该抛物线与y轴的交点为C,求△ABC的面积.
19.为了践行“绿水青山就是金山银山”的发展理念,建设美丽成都,某小区计划在如图所示的一块长为8米,宽为6米的长方形空地上进行绿化,为了不影响人们的出行,需要在中间修建一条通道(图中阴影部分).设绿化所占面积为.
(1)求与的函数表达式;
(2)若要求,已知绿化的费用为每平方米元,修建通道的费用为每平方米40元,问如何设计可使总费用最低,最低费用为多少元?
20.如图,一次函数的图象与坐标轴交于点、,二次函数的图象过、两点.
(1)求二次函数的表达式;
(2)已知点在对称轴上,且点位于轴上方,连接,若,求点的坐标.
21.已知抛物线y=x2+kx+k﹣1.
(1)当k=3时,求抛物线与x轴的两个交点坐标;
(2)无论k取任何实数,抛物线过x轴上一定点,求定点坐标;
(3)当k=5时,设抛物线与y轴交于C点,与x轴交于A,B(点A在点B的左边)两点,连接AC,在线段AC上是否存在点D,使△ABD是直角三角形,若存在,求出点D的坐标,若不存在,请说明理由.
(4)点E(﹣1,1),点F(﹣2,2),抛物线与线段EF只有一个交点,求k的取值范围
22.国庆假期期间,某酒店有20个房间供游客居住,当每个房间每天的定价为100元时,房间恰好全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,酒店需对每个房间每天支出20元的各种费用,设每间房间定价x元().
(1)每天有游客居住的房间数为 (用含有x的式子表示);
(2)当每间房价为多少时,酒店当天的利润为1870元,且总支出最少?
(3)当每间房价定为多少元,酒店的利润W(元)最大,最大利润是多少?
23.如图1,在平面直角坐标系中,直线分别交轴、轴于,两点,经过,两点的抛物线与轴的正半轴相交于点,点为线段上的点,且点的横坐标为.
(1)求抛物线的解析式和直线的解析式;
(2)过作轴的平行线交抛物线于,当是为腰的等腰三角形时,求点的坐标;
(3)若顶点在以、为邻边的平行四边形的形内(不含边界),求m的取值范围.
同课章节目录
