19.2.2 一次函数课件
图片预览








文档简介
课件36张PPT。人教版八年级数学下册19-2.2 一次函数(3)
第 3 课时待定系数法求一次函数的解析式学习难点:学习重点:阅读教材第93页至95页,明确学习目标学习目标:1、学会运用待定系数法和数形结合思想求一次函数解析式;了解两个条件确定一个一次函数;一个条件确定一个正比例函数,能根据函数的图象确定一次函数的表达式,培养学生的数形结合能力.
2、了解分段函数的表示及其图象.
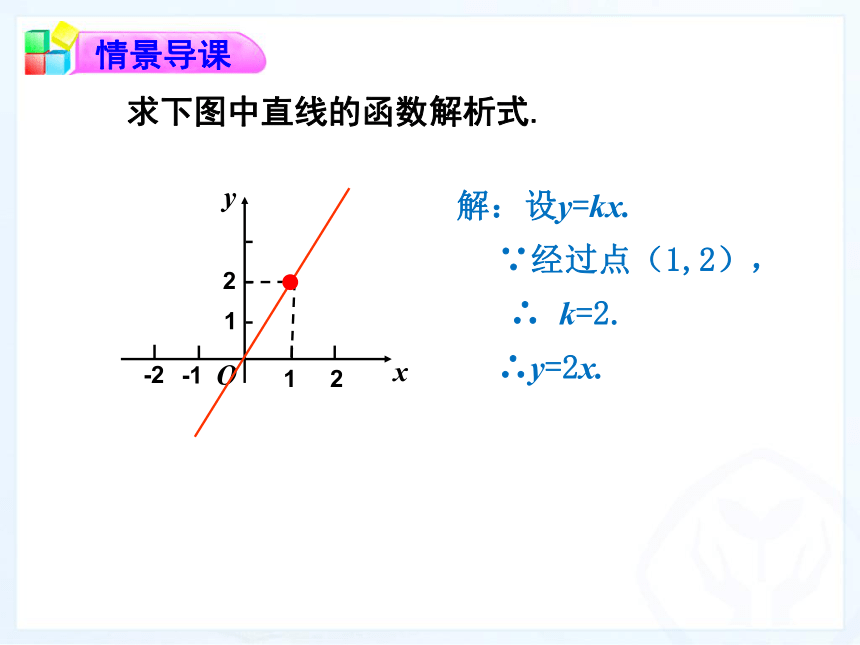
3、能通过函数解决简单的实际问题用待定系数法求一次函数解析式,初步了解分段函数理解分段函数的意义求下图中直线的函数解析式.O2x12-2-11解:设y=kx.∵经过点(1,2),∴ k=2.∴y=2x.y求下图中直线的函数解析式.O1xy12332解:设y=kx+b.∵经过点(2,0), (2,0), 2k+b=0,∴y=-x+2.b=2.解得k=-1,b=2.∴反思小结: 确定正比例函数的解析式需要一个条件,确定一次函数的解析式需要两个条件. 问题1 前面,我们学习了一次函数及其图象和性
质,你能写出两个具体的一次函数解析式吗?如何画出
它们的图象? 思考:
反过来已知一个一次函数的图象经过两个具体的点,
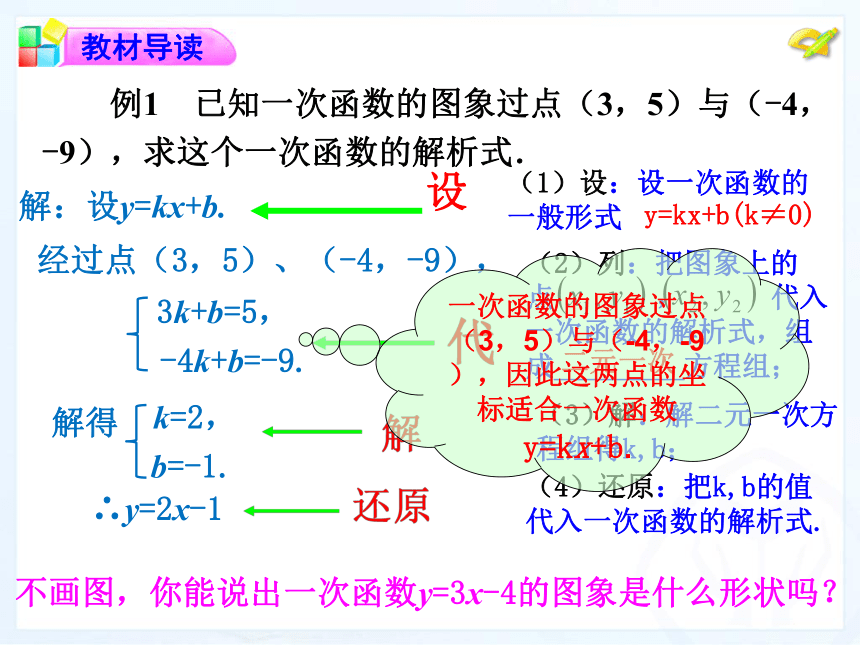
你能求出它的解析式吗?两点法——两点确定一条直线 2.你在画这两个函数图象时,分别描了几个点?你为何选取这几个点?可以有不同取法吗? 例1 已知一次函数的图象过点(3,5)与(-4,
-9),求这个一次函数的解析式. 不画图,你能说出一次函数y=3x-4的图象是什么形状吗?解:设y=kx+b.经过点(3,5)、(-4,-9), 3k+b=5,∴y=2x-1解得k=2,b=-1.-4k+b=-9.(1)设:设一次函数的一般形式 y=kx+b(k≠0)(2)列:把图象上的点 , 代入一次函数的解析式,组成_________方程组;二元一次(3)解:解二元一次方程组得k,b;(4)还原:把k,b的值代入一次函数的解析式.一次函数的图象过点
(3,5)与(-4,-9),因此这两点的坐标适合一次函数y=kx+b. 像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法. 在前面的学习过程中我们发现数与形之间是怎样结合互化的?函数解析式y=kx+b满足条件的两定点一次函数的图象直线画出选取解出选取从数到形从形到数数学的基本思想方法:数形结合 一次函数图像经过点(9,0)和点(24,20),写出函数解析式.解:这个一次函数的解析式为 设这个一次函数的解析式为y=kx+b.把点(9,0)与(24,20)分别代入y=kx+b,得:
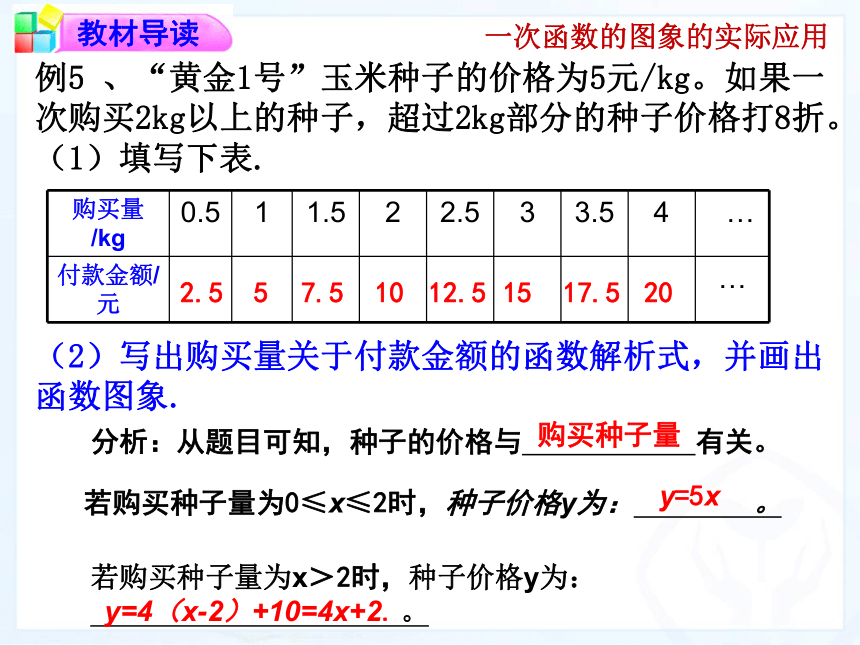
例5 、“黄金1号”玉米种子的价格为5元/kg。如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折。
(1)填写下表.2.557.51012.51517.520一次函数的图象的实际应用(2)写出购买量关于付款金额的函数解析式,并画出函数图象.分析:从题目可知,种子的价格与 有关。若购买种子量为x>2时,种子价格y为:
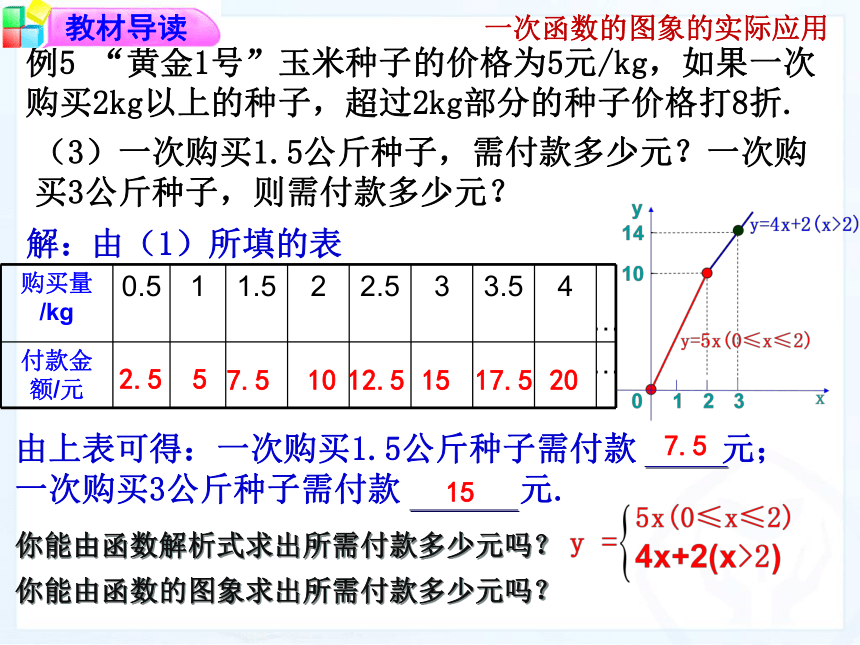
。若购买种子量为0≤x≤2时,种子价格y为: 。购买种子量y=5xy=4(x-2)+10=4x+2. 例5、“黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.(2)写出购买量关于付款金额的函数解析式,并画出函数图象.解:设购买量为x千克,付款金额为y元.当x>2时,y=4(x-2)+10=4x+2.当0≤x≤2时,y=5x;2.557.51012.51517.520y=5x(0≤x≤2)y=4x+2(x>2)函数图象为:一次函数的图象的实际应用例5 “黄金1号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.(3)一次购买1.5公斤种子,需付款多少元?一次购买3公斤种子,则需付款多少元?由上表可得:一次购买1.5公斤种子需付款 元;
一次购买3公斤种子需付款 元.解:由(1)所填的表7.51012.51517.5202.557.515你能由函数解析式求出所需付款多少元吗?你能由函数的图象求出所需付款多少元吗?一次函数的图象的实际应用1、写出两个一次函数,使它们的图象都经过点(-2,3) 2.生物学家研究表明,某种蛇的长度y(cm)是其尾长x(cm)的一次函数,当蛇的尾长为6 cm时,蛇长为45.5 cm;当尾长为14 cm时,蛇长为105.5 cm.当蛇的尾长为10 cm时,这条蛇的长度是多少?综合应用y=7.5x+0.575.5 cm 3、一个函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,-3a)与点(a,6),求这个函数的解析式. 4、小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题: (1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?O40xy123120804y=20x+408个月(1)本节课,我们研究了什么,得到了哪些成果?
(2)用待定系数法求一次函数解析式的解题步骤是
什么?
(3)我们是如何建立一次函数模型解决实际问题的?
(4)书写分段函数的解析式时要注意什么? 1、先设出 ,再根据条件确定,
从而具体写出这个式子的方
法,叫做 .函数解析式解析式中未知的系数 待定系数法1、设—设函数表达式y=kx+b
2、代—将已知条件代入y=kx+b中,列出关于k、b的 方程
3、求—解方程,求k、b的值
4、写—把求出的k、b值代回到表达式中确定一次函数表达式的步骤:教科书 P99习题19.2
第 7,11 题.教科书 P95练习题
第 1、2 题.课后作业1、一个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃。写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
解:(1)由题意得当0≤t≤2时,
y=20;当2y=20+5(t-2)=5t+10函数解析式为:y=20(0≤x≤2)y=5x+10(2 A.A(-1,1) B.B(2,2)
C.C(-2,2) D.D(2,-2)
(2)老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:
甲:函数的图象经过第一象限;
乙:函数的图象经过第二象限;
丙:在每个象限内,y随x的增大而减小.
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数解析式: .
C (3)如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据: ①求出h与d之间的函数解析式(不要求写出自变量d的取值范围).
②某人身高为196 cm,一般情况下他的指距应是多少?解:(1)设h与d之间的函数关系式为:
h=kd+b. 把d=20,h=160,d=21,h=169,
分别代入得,
20k+b=160,
21k+b=169. 解得k=9,b=-20,
即h=9d-20. (2)当h=196时,196=9d-20,解得d=24(cm).
1.用待定系数法求一次函数的解析式
(1)先设出函数解析式,再根据条件确定解析式中未
知数的_______,从而具体写出这个式子的方法,叫做
__________.
(2)探究:已知一次函数的图象经过(2,5)和(-4,2),
求这个一次函数的解析式.系数待定系数法5=2k+b2=-4k+b4用待定系数法求一次函数的解析式(重点)图 1直线 y=kx+b 在坐标系中的图象如图 1,则( ) 思路导引:根据待定系数法求出一次函数的解析式中未知
数的系数. 答案:B
【规律总结】用待定系数法求一次函数的解析式,要根据
题意找出函数上的已知两点坐标.分段函数的解析式 从广州市向北京市打长途电话,按时间收费,3 分钟内收费 2.4 元,每加 1 分钟收费 0.5 元,求时间 t(分)与电话费 y(元)之间的函数解析式,并画出函数的图象.思路导引:分段函数要根据自变量的取值范围分段描述.解:当 0<t≤3 时,y=2.4;当 t>3 时,y=2.4+0.5(t-3)=0.5t+0.9.函数图象由一条线段和一条射线组成,如图 2:图 2【规律总结】分段函数是一个函数而不是多个函数,求出的分段函数解析式必须写出自变量的取值范围. 2.在图 3 中,将直线 OA 向上平移 1 个单位,得到一个一
次函数的图象,那么这个一次函数的解析式是____________.
1.已知一次函数,当 x=-2 时,y=-3;当 x=1 时,
y=3,则这个一次函数的解析式为____________.图 3y=2x+1y=2x+1 图 4
(1)当 x≥30 时,y 与 x 之间的函数解析式为______________;
(2)若小李 4 月份上网 20 小时,他应付________元上网费用;
(3)若小李 5 月份上网费用为 75 元,则他在该月份的上网时间
是__________. 3.某市推出电脑上网包月制,每月收取费用 y(元)与上网时间
x(小时)的函数关系如图 4,其中 BA 是线段,且 BA∥x 轴,AC 是射线.y=3x-306035 下图所表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?我们称此类函数为分段函数.你能写出它的解析式吗?说说你的做法.s=6t;0≤t≤2时,2<t≤4时,s=12;4<t≤6时,s=-6t+12. 问题:为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示. (1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式.
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 .0.9元/度0.5元/度O 春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害. 某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.右图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.请你根据图中信息,针对这种植物判断次日是否需要采取防霜冻措施,并说明理由.解:根据图象可知:
设0时~5时的一次函数关系式为y1=k1x+b1,
经过点(0,3),(5,-3),
b1=3,
5k1+b1=-3.
解得k1=-1.2,
b1=3.
∴y1=-1.2x+3.当y1、y2分别为0时,
而|x2-x1|= >3,
∴应采取防霜冻措施.
设5时~ 8时的一次函数关系式
为y2=k2x+b2,
经过点(5,-3),(8,5),
5k2+b2=-3 ,
8k2+b2=5.
解得 , .
∴ . (2)某市为了鼓励居民节约用水,采用分段计费的方法按月计算每个家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.设某个家庭用水量为x立方米时,应交水费y元. ①分别求出0≤x≤20和x>20时,y与x的函数解析式.②小明家第二季度交纳水费的情况如下:小明家这个季度共用水多少立方米? (1)某同学由甲地出发去乙地,去时以每小时6千米的速度步行2小时到达乙地,在乙地耽搁一小时后,以每小时4千米的速度步行返回甲地,试写出该同学在上述过程中离甲地的距离s(千米)和时间t(小时)的函数解析式,并求出自变量t的取值范围,画出这个函数的图象. 某医药研究所开发了一种新药, 在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(时)的变化如图所示,当成人按规定剂量服药后.
(1)分别求出0≤x≤2和x>2时,y与x之间的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?023x(时)y(微克)1064
第 3 课时待定系数法求一次函数的解析式学习难点:学习重点:阅读教材第93页至95页,明确学习目标学习目标:1、学会运用待定系数法和数形结合思想求一次函数解析式;了解两个条件确定一个一次函数;一个条件确定一个正比例函数,能根据函数的图象确定一次函数的表达式,培养学生的数形结合能力.
2、了解分段函数的表示及其图象.
3、能通过函数解决简单的实际问题用待定系数法求一次函数解析式,初步了解分段函数理解分段函数的意义求下图中直线的函数解析式.O2x12-2-11解:设y=kx.∵经过点(1,2),∴ k=2.∴y=2x.y求下图中直线的函数解析式.O1xy12332解:设y=kx+b.∵经过点(2,0), (2,0), 2k+b=0,∴y=-x+2.b=2.解得k=-1,b=2.∴反思小结: 确定正比例函数的解析式需要一个条件,确定一次函数的解析式需要两个条件. 问题1 前面,我们学习了一次函数及其图象和性
质,你能写出两个具体的一次函数解析式吗?如何画出
它们的图象? 思考:
反过来已知一个一次函数的图象经过两个具体的点,
你能求出它的解析式吗?两点法——两点确定一条直线 2.你在画这两个函数图象时,分别描了几个点?你为何选取这几个点?可以有不同取法吗? 例1 已知一次函数的图象过点(3,5)与(-4,
-9),求这个一次函数的解析式. 不画图,你能说出一次函数y=3x-4的图象是什么形状吗?解:设y=kx+b.经过点(3,5)、(-4,-9), 3k+b=5,∴y=2x-1解得k=2,b=-1.-4k+b=-9.(1)设:设一次函数的一般形式 y=kx+b(k≠0)(2)列:把图象上的点 , 代入一次函数的解析式,组成_________方程组;二元一次(3)解:解二元一次方程组得k,b;(4)还原:把k,b的值代入一次函数的解析式.一次函数的图象过点
(3,5)与(-4,-9),因此这两点的坐标适合一次函数y=kx+b. 像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法. 在前面的学习过程中我们发现数与形之间是怎样结合互化的?函数解析式y=kx+b满足条件的两定点一次函数的图象直线画出选取解出选取从数到形从形到数数学的基本思想方法:数形结合 一次函数图像经过点(9,0)和点(24,20),写出函数解析式.解:这个一次函数的解析式为 设这个一次函数的解析式为y=kx+b.把点(9,0)与(24,20)分别代入y=kx+b,得:
例5 、“黄金1号”玉米种子的价格为5元/kg。如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折。
(1)填写下表.2.557.51012.51517.520一次函数的图象的实际应用(2)写出购买量关于付款金额的函数解析式,并画出函数图象.分析:从题目可知,种子的价格与 有关。若购买种子量为x>2时,种子价格y为:
。若购买种子量为0≤x≤2时,种子价格y为: 。购买种子量y=5xy=4(x-2)+10=4x+2. 例5、“黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.(2)写出购买量关于付款金额的函数解析式,并画出函数图象.解:设购买量为x千克,付款金额为y元.当x>2时,y=4(x-2)+10=4x+2.当0≤x≤2时,y=5x;2.557.51012.51517.520y=5x(0≤x≤2)y=4x+2(x>2)函数图象为:一次函数的图象的实际应用例5 “黄金1号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.(3)一次购买1.5公斤种子,需付款多少元?一次购买3公斤种子,则需付款多少元?由上表可得:一次购买1.5公斤种子需付款 元;
一次购买3公斤种子需付款 元.解:由(1)所填的表7.51012.51517.5202.557.515你能由函数解析式求出所需付款多少元吗?你能由函数的图象求出所需付款多少元吗?一次函数的图象的实际应用1、写出两个一次函数,使它们的图象都经过点(-2,3) 2.生物学家研究表明,某种蛇的长度y(cm)是其尾长x(cm)的一次函数,当蛇的尾长为6 cm时,蛇长为45.5 cm;当尾长为14 cm时,蛇长为105.5 cm.当蛇的尾长为10 cm时,这条蛇的长度是多少?综合应用y=7.5x+0.575.5 cm 3、一个函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,-3a)与点(a,6),求这个函数的解析式. 4、小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题: (1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?O40xy123120804y=20x+408个月(1)本节课,我们研究了什么,得到了哪些成果?
(2)用待定系数法求一次函数解析式的解题步骤是
什么?
(3)我们是如何建立一次函数模型解决实际问题的?
(4)书写分段函数的解析式时要注意什么? 1、先设出 ,再根据条件确定,
从而具体写出这个式子的方
法,叫做 .函数解析式解析式中未知的系数 待定系数法1、设—设函数表达式y=kx+b
2、代—将已知条件代入y=kx+b中,列出关于k、b的 方程
3、求—解方程,求k、b的值
4、写—把求出的k、b值代回到表达式中确定一次函数表达式的步骤:教科书 P99习题19.2
第 7,11 题.教科书 P95练习题
第 1、2 题.课后作业1、一个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃。写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
解:(1)由题意得当0≤t≤2时,
y=20;当2
C.C(-2,2) D.D(2,-2)
(2)老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:
甲:函数的图象经过第一象限;
乙:函数的图象经过第二象限;
丙:在每个象限内,y随x的增大而减小.
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数解析式: .
C (3)如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据: ①求出h与d之间的函数解析式(不要求写出自变量d的取值范围).
②某人身高为196 cm,一般情况下他的指距应是多少?解:(1)设h与d之间的函数关系式为:
h=kd+b. 把d=20,h=160,d=21,h=169,
分别代入得,
20k+b=160,
21k+b=169. 解得k=9,b=-20,
即h=9d-20. (2)当h=196时,196=9d-20,解得d=24(cm).
1.用待定系数法求一次函数的解析式
(1)先设出函数解析式,再根据条件确定解析式中未
知数的_______,从而具体写出这个式子的方法,叫做
__________.
(2)探究:已知一次函数的图象经过(2,5)和(-4,2),
求这个一次函数的解析式.系数待定系数法5=2k+b2=-4k+b4用待定系数法求一次函数的解析式(重点)图 1直线 y=kx+b 在坐标系中的图象如图 1,则( ) 思路导引:根据待定系数法求出一次函数的解析式中未知
数的系数. 答案:B
【规律总结】用待定系数法求一次函数的解析式,要根据
题意找出函数上的已知两点坐标.分段函数的解析式 从广州市向北京市打长途电话,按时间收费,3 分钟内收费 2.4 元,每加 1 分钟收费 0.5 元,求时间 t(分)与电话费 y(元)之间的函数解析式,并画出函数的图象.思路导引:分段函数要根据自变量的取值范围分段描述.解:当 0<t≤3 时,y=2.4;当 t>3 时,y=2.4+0.5(t-3)=0.5t+0.9.函数图象由一条线段和一条射线组成,如图 2:图 2【规律总结】分段函数是一个函数而不是多个函数,求出的分段函数解析式必须写出自变量的取值范围. 2.在图 3 中,将直线 OA 向上平移 1 个单位,得到一个一
次函数的图象,那么这个一次函数的解析式是____________.
1.已知一次函数,当 x=-2 时,y=-3;当 x=1 时,
y=3,则这个一次函数的解析式为____________.图 3y=2x+1y=2x+1 图 4
(1)当 x≥30 时,y 与 x 之间的函数解析式为______________;
(2)若小李 4 月份上网 20 小时,他应付________元上网费用;
(3)若小李 5 月份上网费用为 75 元,则他在该月份的上网时间
是__________. 3.某市推出电脑上网包月制,每月收取费用 y(元)与上网时间
x(小时)的函数关系如图 4,其中 BA 是线段,且 BA∥x 轴,AC 是射线.y=3x-306035 下图所表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?我们称此类函数为分段函数.你能写出它的解析式吗?说说你的做法.s=6t;0≤t≤2时,2<t≤4时,s=12;4<t≤6时,s=-6t+12. 问题:为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示. (1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式.
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 .0.9元/度0.5元/度O 春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害. 某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.右图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.请你根据图中信息,针对这种植物判断次日是否需要采取防霜冻措施,并说明理由.解:根据图象可知:
设0时~5时的一次函数关系式为y1=k1x+b1,
经过点(0,3),(5,-3),
b1=3,
5k1+b1=-3.
解得k1=-1.2,
b1=3.
∴y1=-1.2x+3.当y1、y2分别为0时,
而|x2-x1|= >3,
∴应采取防霜冻措施.
设5时~ 8时的一次函数关系式
为y2=k2x+b2,
经过点(5,-3),(8,5),
5k2+b2=-3 ,
8k2+b2=5.
解得 , .
∴ . (2)某市为了鼓励居民节约用水,采用分段计费的方法按月计算每个家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.设某个家庭用水量为x立方米时,应交水费y元. ①分别求出0≤x≤20和x>20时,y与x的函数解析式.②小明家第二季度交纳水费的情况如下:小明家这个季度共用水多少立方米? (1)某同学由甲地出发去乙地,去时以每小时6千米的速度步行2小时到达乙地,在乙地耽搁一小时后,以每小时4千米的速度步行返回甲地,试写出该同学在上述过程中离甲地的距离s(千米)和时间t(小时)的函数解析式,并求出自变量t的取值范围,画出这个函数的图象. 某医药研究所开发了一种新药, 在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含量最高,达每毫升6微克,接着逐步衰减,10小时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(时)的变化如图所示,当成人按规定剂量服药后.
(1)分别求出0≤x≤2和x>2时,y与x之间的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?023x(时)y(微克)1064
