2023-2024学年沪科版(2012)九年级上册第二十三章解直角三角形单元测试卷(含解析)
文档属性
| 名称 | 2023-2024学年沪科版(2012)九年级上册第二十三章解直角三角形单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 966.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 00:00:00 | ||
图片预览



文档简介
2023-2024学年 沪科版(2012)九年级上册 第二十三章 解直角三角形 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,已知:是斜边上的高线,是斜边上的高线,如果, ,那么等于( )
A.2 B.4.5 C.8 D.12.5
2.如图,某商场有一自动扶梯,其倾斜角为28°,高为7米.用计算器求AB的长,下列按键顺序正确的是( )
A.7×sin28= B.7÷sin28=
C.7×tan28= D.7÷tan28=
3.在中,,,,那么下列结论正确的是( )
A. B. C. D.
4.如图,在中,,,,以点为圆心,长为半径、画弧,与交于点,再分别以,为圆心,大于的长为半径画弧,两弧交于点,.作直线,分别交,于点,,则的长度为( )
A. B. C. D.
5.为庆祝国庆,某校要在如图所示的五角星中(图中所有线段的长度均相等,且),从顶点A开始,沿边每隔40厘米装一盏闪光灯,如果F,J两点间的距离为米,那么需要安装闪光灯的盏数是(参考数据:)
A.30 B.40 C.50 D.60
6.汾河水库位于山西省太原市西北娄烦县境内下静游村至下石家庄之间.如图,水库某段横截面迎水坡的坡度(坡度),若坡高,则坡面的长度约为(参考数据:)
A. B. C. D.
7.在中,,,,则的度数是( ).
A. B. C. D.
8.在中,,是边上的中线,,,则()
A. B. C. D.
9.如图,在中,是边上的高,已知,.下列线段中,其长为的是( )
A. B. C. D.
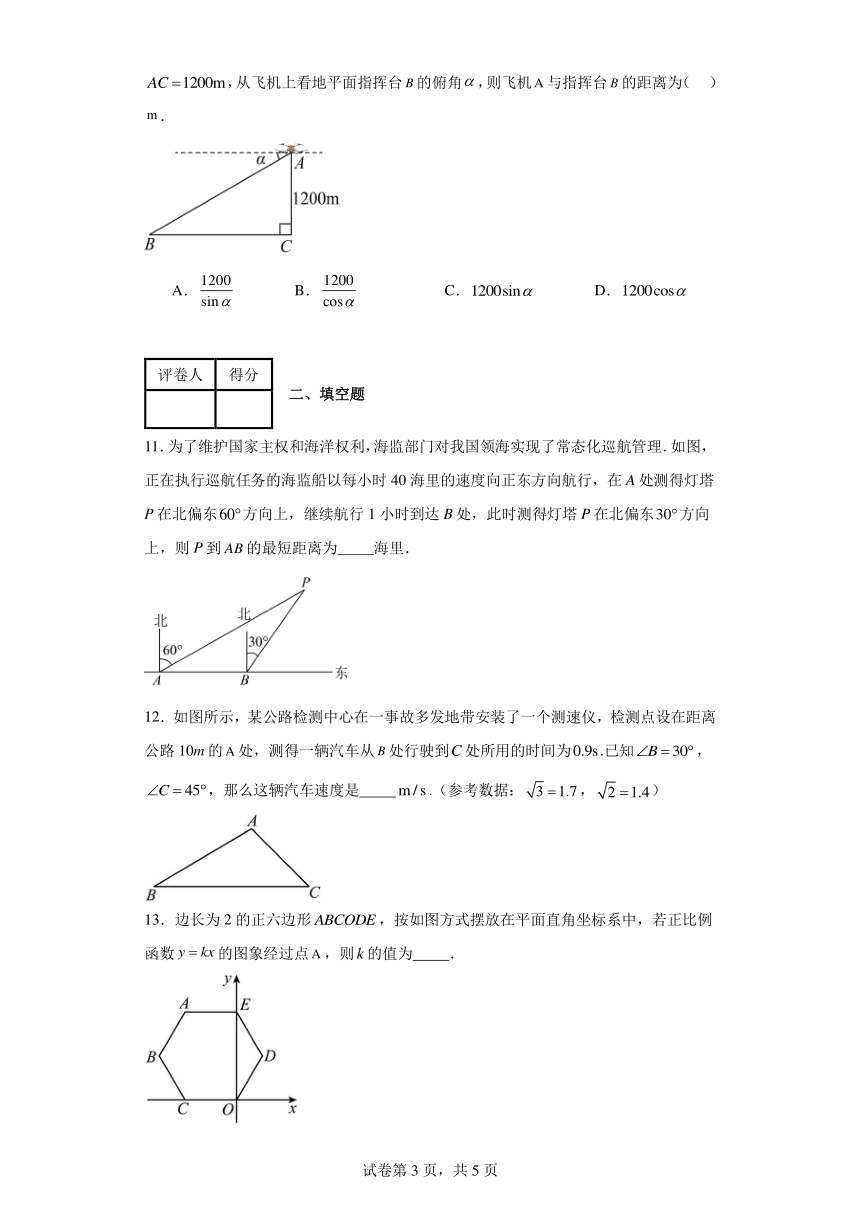
10.如图,某飞机在空中处探测到它的正下方地平面上目标,此时飞行高度,从飞机上看地平面指挥台的俯角,则飞机与指挥台的距离为( ).
A. B. C. D.
评卷人得分
二、填空题
11.为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理.如图,正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行,在A处测得灯塔P在北偏东方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东方向上,则P到的最短距离为 海里.
12.如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的处,测得一辆汽车从处行驶到处所用的时间为.已知,,那么这辆汽车速度是 .(参考数据:,)
13.边长为2的正六边形,按如图方式摆放在平面直角坐标系中,若正比例函数的图象经过点,则的值为 .
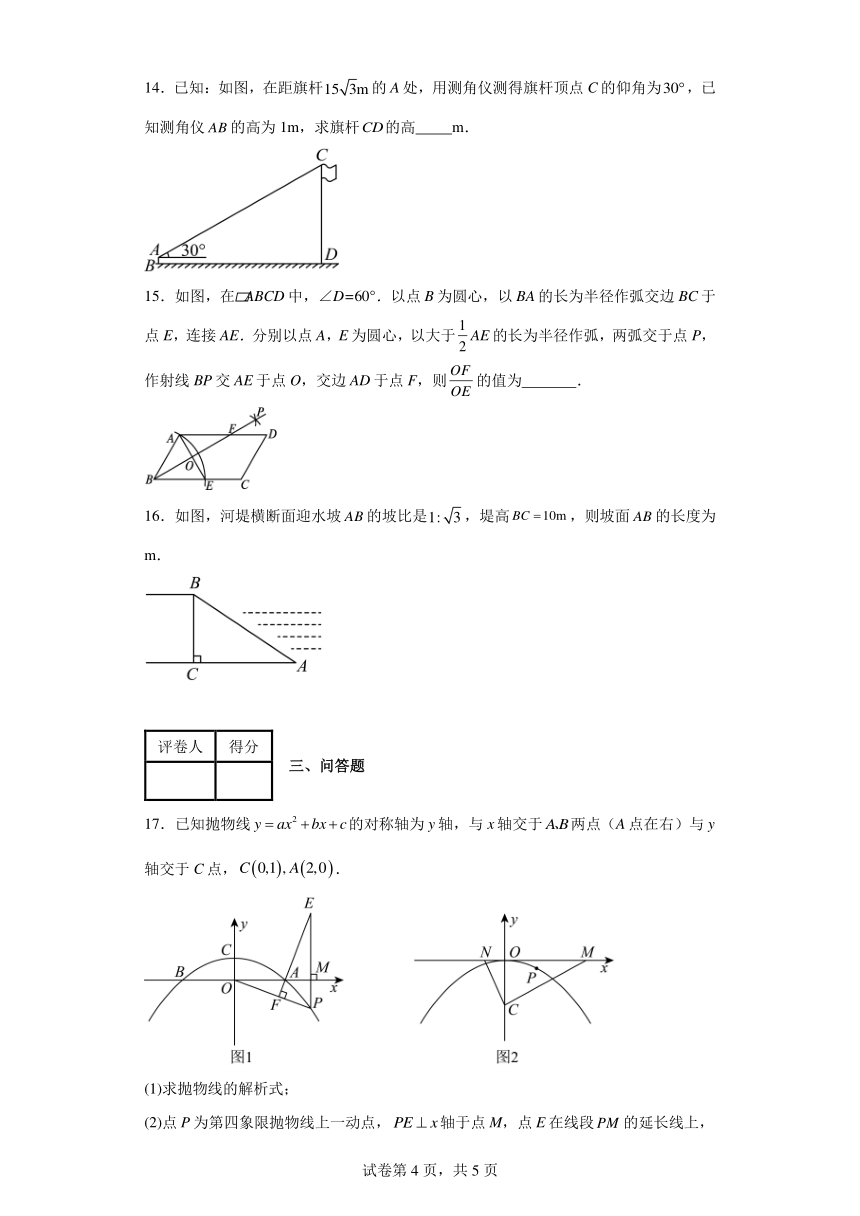
14.已知:如图,在距旗杆的A处,用测角仪测得旗杆顶点C的仰角为,已知测角仪的高为1m,求旗杆的高 m.
15.如图,在 ABCD中,∠D=60°.以点B为圆心,以BA的长为半径作弧交边BC于点E,连接AE.分别以点A,E为圆心,以大于AE的长为半径作弧,两弧交于点P,作射线BP交AE于点O,交边AD于点F,则的值为 .
16.如图,河堤横断面迎水坡的坡比是,堤高,则坡面的长度为 m.
评卷人得分
三、问答题
17.已知抛物线的对称轴为y轴,与x轴交于两点(A点在右)与y轴交于C点,.
(1)求抛物线的解析式;
(2)点P为第四象限抛物线上一动点,轴于点M,点E在线段的延长线上,于点F,问的周长与的比是否为确定的值,并证明你的结论.
(3)如图2,将(1)中抛物线向下平移1个单位,在x轴上,点P在抛物线上,且点P为的外心,,求P点的横坐标.
18.如图,已知,点P是内一点,,垂足为点C,,,A是延长线上一点,连接并延长与射线交于点B.
(1)当点P恰好是线段的中点时,试判断的形状,并说明理由;
(2)当的长度为多少时,是等腰三角形;
(3)设,是否存在适当的k,使得,若存在,试求出k的值;若不存在,试说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查了解直角三角形的应用,相似三角形的判定与性质,设,先证明,根据等角的正切值相等可得,再证明,根据相似三角形面积比等于相似比的平方即可得出结论.
【详解】解:∵,
∴
设,,
∵,,
∴,
∴,,
∴,
∴,
∴,
∴.
∵,
∴,
∵,
∴,
∴,
∵,
∴,
故选:D.
2.B
【详解】由题意,得sin28°=,∴AB=7÷sin28°,∴按键顺序为7÷sin28=.
3.A
【分析】本题主要考查了锐角三角函数的定义,先根据勾股定理求出,再根据锐角三角函数的定义即可解答;理解三角函数的相关定义是解题的关键.
【详解】解:如图:∵,,
∴,
∴.
故选:A.
4.A
【分析】利用勾股定理求出,再根据,解决问题即可.
【详解】解:,,,
,
,
,
垂直平分线段,
,
,
,
.
故选:A.
【点睛】本题考查作图基本作图,勾股定理,线段的垂直平分线的性质,三角函数定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
5.C
【分析】此题考查了等腰三角形三线合一性质,解直角三角形,连接,过点A作,根据等腰三角形三线合一的性质得到,,然后利用代数求出,然后求出总长度,进而求解即可.解题的关键是正确作出辅助线.
【详解】如图所示,连接,过点A作,
根据题意可得,,
∴是等腰三角形,
∵,,
∴,,
∴,即,
解得米,
∴米,
∴米,
∵20米厘米,
∴.
∴需要安装闪光灯的盏数是50.
故选:C.
6.C
【分析】本题考查的是解直角三角形的应用:坡度坡角问题,熟记坡度的概念是解题的关键.
根据坡度的概念求出,再根据勾股定理计算,得到答案.
【详解】解:∵迎水坡的坡度,
由勾股定理得:,
故选:C.
7.A
【分析】本题考查了特殊角的三角函数值,根据余弦的定义得到,然后根据特殊角的三角函数值确定的度数.
【详解】解:∵,,,
∴,
∴.
故选:A.
8.D
【分析】本题考查了解直角三角形,直角三角形斜边上中线的性质,熟练掌握直角三角形斜边上中线的性质和锐角三角函数的定义是解题的关键.
根据直角三角形斜边上中线的性质得,所以,根据勾股定理得,根据锐角三角函数的定义即可求出答案.
【详解】如图,
∵是边上的中线,,
∴,
∴,
∵,
∴,
∴.
故选:D.
9.C
【分析】本题考查正弦的定义,掌握是解题的关键.
【详解】解:∵是边上的高,已知,
∴,
∴,
又∵,,
∴,
故选C.
10.A
【分析】本题考查了解直角三角形,由图得到,利用的正弦即可求解,掌握正弦的定义是解题的关键.
【详解】解:由图可得,,
∴,
∴,
故选:.
11.
【分析】本题考查了解直角三角形的应用-方向角问题.作于D,解直角三角形求出的值即可.
【详解】解:由题意得,,,
∴,
∴,
∴(海里)
过点作于点,
在中,
(海里)
∴P到的最短距离为海里.
故答案为:.
12.30
【分析】本题考查了特殊角的函数值,熟练掌握解斜三角形是解题的关键.过点A作于点D,利用三角函数计算,后计算速度即可.
【详解】如图,过点A作于点D,
根据题意,得,,,
∴,,
解得,
∵汽车从处行驶到处所用的时间为,
∴,
故答案为:30.
13.
【分析】本题考查了待定系数法求正比例函数解析式,正多边形的性质及解直角三角形,过点D作交于点F,通过正六边形的性质和解直角三角形先表示出点A的坐标,再代入正比例函数解析式,即可求解,熟练掌握知识点是解题的关键.
【详解】
如图,过点D作交于点F,
∵正六边形的边长为2,
∴,
∴,,
∴,
∴,
∴点A的坐标为,
将点A的坐标代入,
解得,
故答案为:.
14.
【分析】本题考查的是解直角三角形的实际应用,首先过点A作,交于点E,易证得四边形是矩形,即可得,,然后中,由三角函数的定义,而求得的长,继而求得旗杆的高.
【详解】如图,过点A作,交于点E,
∵,,
∴,
∴四边形是矩形,
∴,,
在中,,
∴,
∴,
答:旗杆的高约.
故答案为:
15.
【详解】∵在 ABCD中,∠D=60°,∴∠ABC=60°,AD∥BC.由作图知BP平分∠ABC,BA=BE,
∴△ABE是等边三角形,∠ABF=∠EBF=∠ABC=30°,
∴BO⊥AE,AO=OE.
∵AD∥BC,
∴∠AFB=∠EBF=30°,
∴∠AFB=∠ABF=30°,
∴AB=AF.
∵BO⊥AE,
∴∠BAO=∠FAO=(180°-30°-30°)=60°,
∴=tan∠FAO=tan 60°=.
16.20
【分析】本题考查直角三角形的应用,根据坡比等于铅直高比上水平宽,求出的长,勾股定理求出的长即可.
【详解】解:由题意,得:,,
∴,
∴;
故答案为:20.
17.(1)
(2)的周长与的比为常数
(3)
【分析】(1) 抛物线的对称轴为轴,则,再把点的坐标代入抛物线表达式,即可求解;
(2)设: 点的坐标为,则 ,得到 ,即可求解;
(3)先证明,则 ,解得:;设点的坐标为 , ;再由确定的第一个关系式; 由得的第二个关系式,两个关系式联立可得的值,即可求解.
【详解】(1)抛物线的对称轴为轴, 则,
抛物线与轴交于点,则则函数为:,
把坐标代入二次函数表达式得:,
解得:,
抛物线的表达式为:;
(2)设: 点的坐标为,则,
则点、,
∴,
∴,
则的周长,
故的周长与的比为常数;
(3)抛物线向下平移个单位,得到的抛物线为:
过点作轴的垂线,交轴于点,连接并延长交于点,
则直线为的角平分线,即:,
,,
,
,
设:
则点的坐标分别为,
,即: ,
,
设: 点的坐标为,
,
,
点在抛物线上,则,
即: ①,
∵,
即:,
联立①②解得:,
∴点的横坐标.
【点睛】本题考查的是二次函数综合应用,涉及到解直角三角形、三角形相似的判定和性质、三角形外心等知识点,掌握解直角三角形是解题的关键.
18.(1)是直角三角形,理由见解析
(2)的值为或或1
(3)存在,k的值为
【分析】(1)如图,作于,证明,则,即,解得,,,由,可得,解得,,由,可得,由,可得,然后作答即可;
(2)设,,则, ,,,由勾股定理得,证明,则,即,解得,,,,由题意知,当是等腰三角形时,分①,②,③,三种情况,根据等量关系进行求解即可;
(2)同理(2),则,,,由,,可得,,则,结合,计算求出满足要求的的解,进而可求.
【详解】(1)解:是直角三角形,理由如下:
∵点P恰好是线段的中点,
∴,
如图,作于,
∵,
∴,
∴,
∴,即,解得,,,
∴,
∵,
∴,解得,,
∴,,
∴,
∴,
∵,
∴,
∴是直角三角形;
(2)解:设,,则, ,,,
由勾股定理得,
∵,
∴,
∴,即,解得,,
∴,,
由题意知,当是等腰三角形时,分①,②,③,三种情况求解;
①当时,则,解得,;
②当时,则,解得,;
③当时,则,解得,或(舍去);
综上所述,的值为或或1;
(3)解:同理(2),则,,
∴,
∵,,
∴,解得,,
∵,
∴,
解得,,
∵,
∴,
解得,或(舍去),
∴,
∴存在,k的值为.
【点睛】本题考查了相似三角形的判定与性质,等腰三角形的性质,勾股定理,正切,三角形内角和等知识.熟练掌握相似三角形的判定与性质,等腰三角形的性质,正切是解题的关键.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.如图,已知:是斜边上的高线,是斜边上的高线,如果, ,那么等于( )
A.2 B.4.5 C.8 D.12.5
2.如图,某商场有一自动扶梯,其倾斜角为28°,高为7米.用计算器求AB的长,下列按键顺序正确的是( )
A.7×sin28= B.7÷sin28=
C.7×tan28= D.7÷tan28=
3.在中,,,,那么下列结论正确的是( )
A. B. C. D.
4.如图,在中,,,,以点为圆心,长为半径、画弧,与交于点,再分别以,为圆心,大于的长为半径画弧,两弧交于点,.作直线,分别交,于点,,则的长度为( )
A. B. C. D.
5.为庆祝国庆,某校要在如图所示的五角星中(图中所有线段的长度均相等,且),从顶点A开始,沿边每隔40厘米装一盏闪光灯,如果F,J两点间的距离为米,那么需要安装闪光灯的盏数是(参考数据:)
A.30 B.40 C.50 D.60
6.汾河水库位于山西省太原市西北娄烦县境内下静游村至下石家庄之间.如图,水库某段横截面迎水坡的坡度(坡度),若坡高,则坡面的长度约为(参考数据:)
A. B. C. D.
7.在中,,,,则的度数是( ).
A. B. C. D.
8.在中,,是边上的中线,,,则()
A. B. C. D.
9.如图,在中,是边上的高,已知,.下列线段中,其长为的是( )
A. B. C. D.
10.如图,某飞机在空中处探测到它的正下方地平面上目标,此时飞行高度,从飞机上看地平面指挥台的俯角,则飞机与指挥台的距离为( ).
A. B. C. D.
评卷人得分
二、填空题
11.为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理.如图,正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行,在A处测得灯塔P在北偏东方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东方向上,则P到的最短距离为 海里.
12.如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的处,测得一辆汽车从处行驶到处所用的时间为.已知,,那么这辆汽车速度是 .(参考数据:,)
13.边长为2的正六边形,按如图方式摆放在平面直角坐标系中,若正比例函数的图象经过点,则的值为 .
14.已知:如图,在距旗杆的A处,用测角仪测得旗杆顶点C的仰角为,已知测角仪的高为1m,求旗杆的高 m.
15.如图,在 ABCD中,∠D=60°.以点B为圆心,以BA的长为半径作弧交边BC于点E,连接AE.分别以点A,E为圆心,以大于AE的长为半径作弧,两弧交于点P,作射线BP交AE于点O,交边AD于点F,则的值为 .
16.如图,河堤横断面迎水坡的坡比是,堤高,则坡面的长度为 m.
评卷人得分
三、问答题
17.已知抛物线的对称轴为y轴,与x轴交于两点(A点在右)与y轴交于C点,.
(1)求抛物线的解析式;
(2)点P为第四象限抛物线上一动点,轴于点M,点E在线段的延长线上,于点F,问的周长与的比是否为确定的值,并证明你的结论.
(3)如图2,将(1)中抛物线向下平移1个单位,在x轴上,点P在抛物线上,且点P为的外心,,求P点的横坐标.
18.如图,已知,点P是内一点,,垂足为点C,,,A是延长线上一点,连接并延长与射线交于点B.
(1)当点P恰好是线段的中点时,试判断的形状,并说明理由;
(2)当的长度为多少时,是等腰三角形;
(3)设,是否存在适当的k,使得,若存在,试求出k的值;若不存在,试说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查了解直角三角形的应用,相似三角形的判定与性质,设,先证明,根据等角的正切值相等可得,再证明,根据相似三角形面积比等于相似比的平方即可得出结论.
【详解】解:∵,
∴
设,,
∵,,
∴,
∴,,
∴,
∴,
∴,
∴.
∵,
∴,
∵,
∴,
∴,
∵,
∴,
故选:D.
2.B
【详解】由题意,得sin28°=,∴AB=7÷sin28°,∴按键顺序为7÷sin28=.
3.A
【分析】本题主要考查了锐角三角函数的定义,先根据勾股定理求出,再根据锐角三角函数的定义即可解答;理解三角函数的相关定义是解题的关键.
【详解】解:如图:∵,,
∴,
∴.
故选:A.
4.A
【分析】利用勾股定理求出,再根据,解决问题即可.
【详解】解:,,,
,
,
,
垂直平分线段,
,
,
,
.
故选:A.
【点睛】本题考查作图基本作图,勾股定理,线段的垂直平分线的性质,三角函数定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
5.C
【分析】此题考查了等腰三角形三线合一性质,解直角三角形,连接,过点A作,根据等腰三角形三线合一的性质得到,,然后利用代数求出,然后求出总长度,进而求解即可.解题的关键是正确作出辅助线.
【详解】如图所示,连接,过点A作,
根据题意可得,,
∴是等腰三角形,
∵,,
∴,,
∴,即,
解得米,
∴米,
∴米,
∵20米厘米,
∴.
∴需要安装闪光灯的盏数是50.
故选:C.
6.C
【分析】本题考查的是解直角三角形的应用:坡度坡角问题,熟记坡度的概念是解题的关键.
根据坡度的概念求出,再根据勾股定理计算,得到答案.
【详解】解:∵迎水坡的坡度,
由勾股定理得:,
故选:C.
7.A
【分析】本题考查了特殊角的三角函数值,根据余弦的定义得到,然后根据特殊角的三角函数值确定的度数.
【详解】解:∵,,,
∴,
∴.
故选:A.
8.D
【分析】本题考查了解直角三角形,直角三角形斜边上中线的性质,熟练掌握直角三角形斜边上中线的性质和锐角三角函数的定义是解题的关键.
根据直角三角形斜边上中线的性质得,所以,根据勾股定理得,根据锐角三角函数的定义即可求出答案.
【详解】如图,
∵是边上的中线,,
∴,
∴,
∵,
∴,
∴.
故选:D.
9.C
【分析】本题考查正弦的定义,掌握是解题的关键.
【详解】解:∵是边上的高,已知,
∴,
∴,
又∵,,
∴,
故选C.
10.A
【分析】本题考查了解直角三角形,由图得到,利用的正弦即可求解,掌握正弦的定义是解题的关键.
【详解】解:由图可得,,
∴,
∴,
故选:.
11.
【分析】本题考查了解直角三角形的应用-方向角问题.作于D,解直角三角形求出的值即可.
【详解】解:由题意得,,,
∴,
∴,
∴(海里)
过点作于点,
在中,
(海里)
∴P到的最短距离为海里.
故答案为:.
12.30
【分析】本题考查了特殊角的函数值,熟练掌握解斜三角形是解题的关键.过点A作于点D,利用三角函数计算,后计算速度即可.
【详解】如图,过点A作于点D,
根据题意,得,,,
∴,,
解得,
∵汽车从处行驶到处所用的时间为,
∴,
故答案为:30.
13.
【分析】本题考查了待定系数法求正比例函数解析式,正多边形的性质及解直角三角形,过点D作交于点F,通过正六边形的性质和解直角三角形先表示出点A的坐标,再代入正比例函数解析式,即可求解,熟练掌握知识点是解题的关键.
【详解】
如图,过点D作交于点F,
∵正六边形的边长为2,
∴,
∴,,
∴,
∴,
∴点A的坐标为,
将点A的坐标代入,
解得,
故答案为:.
14.
【分析】本题考查的是解直角三角形的实际应用,首先过点A作,交于点E,易证得四边形是矩形,即可得,,然后中,由三角函数的定义,而求得的长,继而求得旗杆的高.
【详解】如图,过点A作,交于点E,
∵,,
∴,
∴四边形是矩形,
∴,,
在中,,
∴,
∴,
答:旗杆的高约.
故答案为:
15.
【详解】∵在 ABCD中,∠D=60°,∴∠ABC=60°,AD∥BC.由作图知BP平分∠ABC,BA=BE,
∴△ABE是等边三角形,∠ABF=∠EBF=∠ABC=30°,
∴BO⊥AE,AO=OE.
∵AD∥BC,
∴∠AFB=∠EBF=30°,
∴∠AFB=∠ABF=30°,
∴AB=AF.
∵BO⊥AE,
∴∠BAO=∠FAO=(180°-30°-30°)=60°,
∴=tan∠FAO=tan 60°=.
16.20
【分析】本题考查直角三角形的应用,根据坡比等于铅直高比上水平宽,求出的长,勾股定理求出的长即可.
【详解】解:由题意,得:,,
∴,
∴;
故答案为:20.
17.(1)
(2)的周长与的比为常数
(3)
【分析】(1) 抛物线的对称轴为轴,则,再把点的坐标代入抛物线表达式,即可求解;
(2)设: 点的坐标为,则 ,得到 ,即可求解;
(3)先证明,则 ,解得:;设点的坐标为 , ;再由确定的第一个关系式; 由得的第二个关系式,两个关系式联立可得的值,即可求解.
【详解】(1)抛物线的对称轴为轴, 则,
抛物线与轴交于点,则则函数为:,
把坐标代入二次函数表达式得:,
解得:,
抛物线的表达式为:;
(2)设: 点的坐标为,则,
则点、,
∴,
∴,
则的周长,
故的周长与的比为常数;
(3)抛物线向下平移个单位,得到的抛物线为:
过点作轴的垂线,交轴于点,连接并延长交于点,
则直线为的角平分线,即:,
,,
,
,
设:
则点的坐标分别为,
,即: ,
,
设: 点的坐标为,
,
,
点在抛物线上,则,
即: ①,
∵,
即:,
联立①②解得:,
∴点的横坐标.
【点睛】本题考查的是二次函数综合应用,涉及到解直角三角形、三角形相似的判定和性质、三角形外心等知识点,掌握解直角三角形是解题的关键.
18.(1)是直角三角形,理由见解析
(2)的值为或或1
(3)存在,k的值为
【分析】(1)如图,作于,证明,则,即,解得,,,由,可得,解得,,由,可得,由,可得,然后作答即可;
(2)设,,则, ,,,由勾股定理得,证明,则,即,解得,,,,由题意知,当是等腰三角形时,分①,②,③,三种情况,根据等量关系进行求解即可;
(2)同理(2),则,,,由,,可得,,则,结合,计算求出满足要求的的解,进而可求.
【详解】(1)解:是直角三角形,理由如下:
∵点P恰好是线段的中点,
∴,
如图,作于,
∵,
∴,
∴,
∴,即,解得,,,
∴,
∵,
∴,解得,,
∴,,
∴,
∴,
∵,
∴,
∴是直角三角形;
(2)解:设,,则, ,,,
由勾股定理得,
∵,
∴,
∴,即,解得,,
∴,,
由题意知,当是等腰三角形时,分①,②,③,三种情况求解;
①当时,则,解得,;
②当时,则,解得,;
③当时,则,解得,或(舍去);
综上所述,的值为或或1;
(3)解:同理(2),则,,
∴,
∵,,
∴,解得,,
∵,
∴,
解得,,
∵,
∴,
解得,或(舍去),
∴,
∴存在,k的值为.
【点睛】本题考查了相似三角形的判定与性质,等腰三角形的性质,勾股定理,正切,三角形内角和等知识.熟练掌握相似三角形的判定与性质,等腰三角形的性质,正切是解题的关键.
答案第1页,共2页
答案第1页,共2页
