2023-2024学年沪科版(2012)九年级上册第二十一章二次函数与反比例函数单元测试卷(含解析)
文档属性
| 名称 | 2023-2024学年沪科版(2012)九年级上册第二十一章二次函数与反比例函数单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 693.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-17 23:52:00 | ||
图片预览




文档简介
2023-2024学年 沪科版(2012)九年级上册 第二十一章 二次函数与反比例函数 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.若,,为二次函数图象上的三点,则,,的大小关系是( )
A. B. C. D.
2.如图,反比例函数与正比例函数相交于点和点,则点的坐标为( ).
A. B. C. D.
3.如图,在平面直角坐标系中,点在反比例函数(为常数,)的图象上,轴,垂足为,连接,的是面积为6,则的值为( )
A.3 B.6 C.9 D.12
4.已知点和点是双曲线上的两个点,如果,那么与的大小关系正确的是( )
A. B. C. D.无法判断
5.如图,拋物线与轴交于点、,与轴交于点,,则下列各式成立的是( )
A. B. C. D.
6.在平面直角坐标系中,下列函数的图象经过点的是( )
A. B. C. D.
7.在反比例函数为常数)上有三点,,,,,若,则,,的大小关系为( )
A. B. C. D.
8.将抛物线向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )
A. B. C. D.
9.下面的四个问题中,变量与变量之间的函数关系可以用如图所示的图象表示的是( )
A.汽车从甲地匀速行驶到乙地,剩余路程与行驶时间
B.当电压一定时,通过某用电器的电流与该用电器的电阻
C.圆锥的母线长等于底面圆的直径,其侧面积与底面圆的半径
D.用长度一定的铁丝围成一个矩形,矩形的面积与一边长
10.已知二次函数的图象与x轴的一个交点坐标是,则关于x的一元二次方程的两个实数根是( )
A., B., C., D.,
评卷人得分
二、填空题
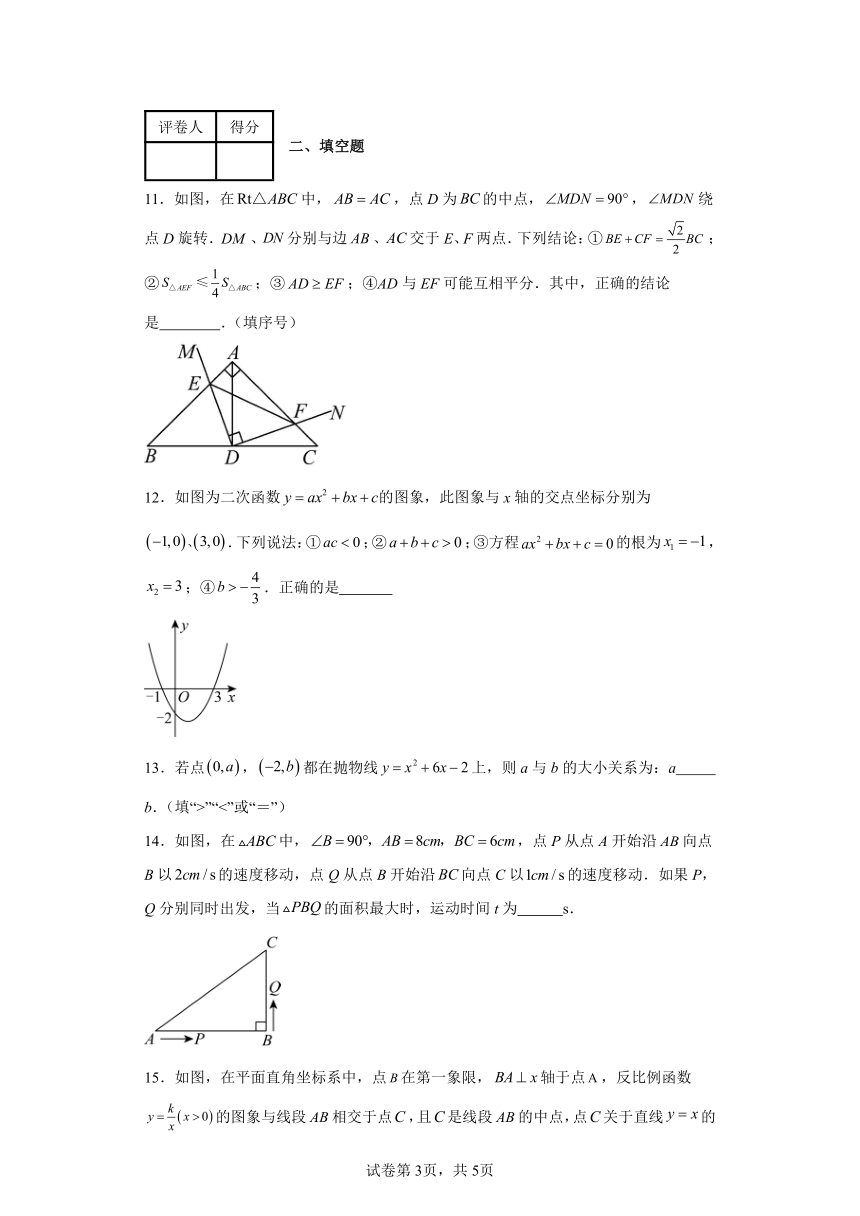
11.如图,在中,,点D为的中点,,绕点D旋转.、分别与边、交于E、F两点.下列结论:①;②;③;④AD与EF可能互相平分.其中,正确的结论是 .(填序号)
12.如图为二次函数的图象,此图象与x轴的交点坐标分别为.下列说法:①;②;③方程的根为,;④.正确的是
13.若点,都在抛物线上,则a与b的大小关系为:a b.(填“>”“<”或“=”)
14.如图,在中,,点P从点A开始沿向点B以的速度移动,点Q从点B开始沿向点C以的速度移动.如果P,Q分别同时出发,当的面积最大时,运动时间t为 s.
15.如图,在平面直角坐标系中,点在第一象限,轴于点,反比例函数的图象与线段相交于点,且是线段的中点,点关于直线的对称点的坐标为,若的面积为3,则的值为
16.已知点在双曲线上,过点向轴作垂线,垂足为.如果,那么 .
评卷人得分
三、问答题
17.商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件,据此规律,请回答:
(1)当每件商品售价定为元时,每天可销售y件商品,商场获得的日盈利是w元,请分别写出y关于x的函数关系式及w关于x的函数关系式;
(2)在上述条件不变,商品销售正常的情况下,每件商品的售价定为多少元,商场日盈利最大,最大利润为多少?
18.水平方向抛出一个有弹性的小球,小球的运动路线是抛物线,触地后,小球会弹起,每次弹起的高度都是之前下落高度的,且水平方向飞行的距离也是原来的,这样到达最高点后又继续下落,下落的飞行轨迹与刚才弹起的飞行轨迹是对称的,如此下去,小球会划出一道优美的“波浪线”.如图是小球的一部分飞行路线,小球第一次下落的抛物线解析式为,落到水平地面上的处,第一次反弹到最高点处,然后下落到更低的地面上的处(两处地面落差),然后又弹起到最高点处.
(1)求小球第一次下落的水平飞行距离;
(2)求点的坐标;
(3)直接写出与的高度差.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题主要考查了比较二次函数值的大小,根据开口向上的二次函数,离对称轴越远,函数值越大,只需要比较出A、B、C三点离对称轴距离的大小即可得到答案.
【详解】解:∵二次函数解析式为,,
∴二次函数开口向上,对称轴为直线,
∴离对称轴越远,函数值越大,
∵,,为二次函数图象上的三点,,
∴.
故选:B.
2.A
【分析】本题考查反比例函数与正比例函数图像交点问题,根据反比例函数与正比例函数相交于点,得到反比例函数与正比例函数的解析式,再联立方程组求解,即可得到点坐标.
【详解】解:∵反比例函数与正比例函数相交于点,
∴点在反比例函数与正比例函数图像上,满足函数解析式,
∴将代入到,得到;
同理将代入到,得到,
联立方程组
解得,,.
故选:A
3.D
【分析】本题主要考查了的几何意义,用表示三角形的面积是本题的解题关键.
【详解】解:的面积为,
.
故选:D.
4.D
【分析】本题考查了反比例函数的图像与性质,由于点不一定在同一象限,所以无法判断出的大小.
【详解】∵,
∴双曲线在第二、四象限,
①当时,;
②当时,;
③当时,;
综上,无法判断出的大小,
故选:D.
5.C
【分析】本题考查了二次函数综合问题;根据,有,可设点、的坐标为,代入解析式,即可解得答案.
【详解】解:,则是等腰直角三角形
,
可设点、的坐标为,
把代入,得
即,
,
,即.
故选:C.
6.A
【分析】本题考查了反比例函数图象上点的坐标特征,一次函数图象上点的坐标特征,二次函数函数图象上点的坐标特征,根据它们的坐标特征判断即可.
【详解】解:A、抛物线经过点,故符合题意;
B、双曲线不经过点,故不符合题意;
C、抛物线不经过点,故不符合题意;
D、直线不经过点,故不符合题意;
故选:A.
7.A
【分析】本题主要考查反比例函数图象的特点,熟练掌握反比例函数的图象的特点是解决本题的关键.根据偶次方的非负性,得,再根据反比例函数的图象的特点解决此题.
【详解】解:,
.
反比例函数为常数)的函数图象在第一、第三象限;在第一象限内,随着的增大而减小;在第三象限内,随着的增大而减小.
,
,,即.
故选:A
8.A
【分析】根据“上加下减,左加右减”的原则进行解答即可.此题考查了二次函数图象的平移与几何变换,利用抛物线解析式的变化规律:左加右减,上加下减是解题关键.
【详解】解:将将抛物线向左平移3个单位长度所得抛物线解析式为:,即;
再向下平移2个单位为:,即,
故选:A.
9.D
【分析】本题考查了函数的图象和函数关系式,理解题意是解题的关键.根据每个选项的意义,找出它们之间的函数关系,逐一判断.
【详解】解:A.汽车从甲地匀速行驶到乙地,剩余路程是行驶时间的一次函数,图象应该是线段,故A不符合题意;
B.当电压一定时,通过某用电器的电流与该用电器的电阻成反比例关系,图象应该是双曲线的一支,故B不符合题意;
C.圆锥的母线长等于底面圆的直径,其侧面积与底面圆的半径成二次函数关系,开口向上,故C不符合题意;
D.用长度一定的铁丝围成一个矩形,矩形的面积与一边长成二次函数关系,开口向下,故D符合题意;
故选:D.
10.A
【分析】本题考查了抛物线与x轴的交点,先求出抛物线的对称轴,在求出抛物线与x轴的另一个交点,最后根据抛物线与一元二次方程的关系求解.
【详解】解:∵抛物线的对称轴为:,图象与x轴的一个交点坐标是,
∴根据抛物线的对称性得抛物线与x轴的另一个交点是,
∴关于x的一元二次方程的两个实数根是:,,
故选:A.
11.①②④
【分析】先由证明,得出,再由勾股定理即可得出,从而判断①;设,,先由三角形的面积公式得出,,再根据二次函数的性质即可判断②;由勾股定理得到的表达式,利用二次函数性质求得最小值为,而,所以,从而③错误;如果四边形为平行四边形,则与互相平分,此时,,又为中点,所以当、分别为、的中点时,与互相平分,从而判断④.
【详解】解:中,,点为中点,
,,
,
,
.
在与中,
,
,
,
在中,.
故①正确;
设,,则.
,
当时,有最大值,
又,
.
故②正确;
,
当时,取得最小值,
(等号当且仅当时成立),
而,
.
故③错误;
当、分别为、的中点时,
∵,点D为的中点,
∴,
∵、分别为、的中点
∴,,
∴
∴四边形为正方形,此时与互相平分.
故④正确.
综上所述,正确的有:①②④.
故答案为:①②④.
【点睛】本题主要考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,三角形的面积,二次函数的性质等知识,综合性较强,有一定难度.
12.①③④
【分析】本题主要考查了二次函数的图象和性质,①由抛物线的开口方向、与y轴的交点判定a、c的符号;②将代入函数关系式,结合图象判定y的符号;③根据二次函数图象与x轴的交点解答;④利用二次函数图象与x轴的交点可得,再由,可作出判断.
【详解】解:观察函数图象得:抛物线开口向上,且与y轴交于负半轴,
∴,
∴,故①正确;
根据抛物线的图象得:该抛物线的对称轴是直线,
∴当时,,
即;故②错误;
③∵的图象与x轴的交点坐标分别为,
∴方程的根为,,故③正确;
∵的图象与x轴的交点坐标分别为,
∴,
∴,
观察图象得:,
∴,
∴,故④正确;
故答案为:①③④.
13.
【分析】本题考查的是比较二次函数的函数值的大小,选择合适的方法比较函数值的大小是解本题的关键,本题把点的坐标代入函数解析式先计算,再比较即可.
【详解】解:把点,代入,
∴,,
∴,
故答案为:
14.2
【分析】求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数的绝对值是较小的整数时,用配方法较好.
本题考查二次函数最大(小)值的求法.先用含的代数式表示出、再根据三角形的面积公式计算.
【详解】解:根据题意得,
三角形面积为:
∴当时,的面积最大为,
故答案为:2.
15.3
【分析】本题考查了反比例函数的比例系数的几何意义、与中线有关的三角形的面积,熟记反比例函数的比例系数的几何意义是解题的关键.连接,先求出,再根据反比例函数的比例系数的几何意义求解即可得.
【详解】解:如图,连接,
是线段的中点,的面积为3,
,
由反比例函数的图象可知,,
在反比例函数的图象,
,
解得,
故答案为:3.
16.
【分析】本题考查反比例函数系数的几何意义,根据反比例函数的的几何意义即可直接求解.
【详解】当在第一象限或第三象限时,,
当在第二象限或第四象限时,.
故答案是:.
17.(1);
(2)每件商品的销售价定为160元,商场日盈利最大,最大利润为1600元
【分析】本题考查二次函数的应用,关键是根据等量关系列出函数解析式和掌握二次函数的性质.
(1)根据每天可销售=涨价前每天可销售量-涨价减小的销售量,总利润单件利润销售数量,列出函数解析式即可;
(2)根据日盈利每件利润销售数量列出函数关系式,根据函数的性质求最值.
【详解】(1)解:由题意,得
即,
∴
即
(2)解:∵,
,
当时,有最大值,最大值为1600,
每件商品的销售价定为160元,商场日盈利最大,最大利润为1600元.
18.(1)
(2)
(3)
【分析】本题主要考查二次函数的应用,熟练掌握二次函数的图像和性质是解题的关键.
(1)根据二次函数与轴的交点得出点坐标,即可得到答案.
(2)求出第二次弹起的高度以及水平距离,根据函数图形的性质即可求出答案;
(3)求出的垂直距离即可得到答案.
【详解】(1)解:,
当时,,
解得,
;
(2)解:每次弹起的高度都是之前下落高度的,且水平方向飞行的距离也是原来的,
第一次弹起的高度为,水平距离
故第二次弹起的高度为,水平距离,
故第二次函数图像解析式为
时,
解得或,
故;
(3)解:由题意知第三次下落的高度为,
故第三次弹起的高度为,
故点的垂直距离为,
故与的高度差为.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题
1.若,,为二次函数图象上的三点,则,,的大小关系是( )
A. B. C. D.
2.如图,反比例函数与正比例函数相交于点和点,则点的坐标为( ).
A. B. C. D.
3.如图,在平面直角坐标系中,点在反比例函数(为常数,)的图象上,轴,垂足为,连接,的是面积为6,则的值为( )
A.3 B.6 C.9 D.12
4.已知点和点是双曲线上的两个点,如果,那么与的大小关系正确的是( )
A. B. C. D.无法判断
5.如图,拋物线与轴交于点、,与轴交于点,,则下列各式成立的是( )
A. B. C. D.
6.在平面直角坐标系中,下列函数的图象经过点的是( )
A. B. C. D.
7.在反比例函数为常数)上有三点,,,,,若,则,,的大小关系为( )
A. B. C. D.
8.将抛物线向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )
A. B. C. D.
9.下面的四个问题中,变量与变量之间的函数关系可以用如图所示的图象表示的是( )
A.汽车从甲地匀速行驶到乙地,剩余路程与行驶时间
B.当电压一定时,通过某用电器的电流与该用电器的电阻
C.圆锥的母线长等于底面圆的直径,其侧面积与底面圆的半径
D.用长度一定的铁丝围成一个矩形,矩形的面积与一边长
10.已知二次函数的图象与x轴的一个交点坐标是,则关于x的一元二次方程的两个实数根是( )
A., B., C., D.,
评卷人得分
二、填空题
11.如图,在中,,点D为的中点,,绕点D旋转.、分别与边、交于E、F两点.下列结论:①;②;③;④AD与EF可能互相平分.其中,正确的结论是 .(填序号)
12.如图为二次函数的图象,此图象与x轴的交点坐标分别为.下列说法:①;②;③方程的根为,;④.正确的是
13.若点,都在抛物线上,则a与b的大小关系为:a b.(填“>”“<”或“=”)
14.如图,在中,,点P从点A开始沿向点B以的速度移动,点Q从点B开始沿向点C以的速度移动.如果P,Q分别同时出发,当的面积最大时,运动时间t为 s.
15.如图,在平面直角坐标系中,点在第一象限,轴于点,反比例函数的图象与线段相交于点,且是线段的中点,点关于直线的对称点的坐标为,若的面积为3,则的值为
16.已知点在双曲线上,过点向轴作垂线,垂足为.如果,那么 .
评卷人得分
三、问答题
17.商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件,据此规律,请回答:
(1)当每件商品售价定为元时,每天可销售y件商品,商场获得的日盈利是w元,请分别写出y关于x的函数关系式及w关于x的函数关系式;
(2)在上述条件不变,商品销售正常的情况下,每件商品的售价定为多少元,商场日盈利最大,最大利润为多少?
18.水平方向抛出一个有弹性的小球,小球的运动路线是抛物线,触地后,小球会弹起,每次弹起的高度都是之前下落高度的,且水平方向飞行的距离也是原来的,这样到达最高点后又继续下落,下落的飞行轨迹与刚才弹起的飞行轨迹是对称的,如此下去,小球会划出一道优美的“波浪线”.如图是小球的一部分飞行路线,小球第一次下落的抛物线解析式为,落到水平地面上的处,第一次反弹到最高点处,然后下落到更低的地面上的处(两处地面落差),然后又弹起到最高点处.
(1)求小球第一次下落的水平飞行距离;
(2)求点的坐标;
(3)直接写出与的高度差.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】本题主要考查了比较二次函数值的大小,根据开口向上的二次函数,离对称轴越远,函数值越大,只需要比较出A、B、C三点离对称轴距离的大小即可得到答案.
【详解】解:∵二次函数解析式为,,
∴二次函数开口向上,对称轴为直线,
∴离对称轴越远,函数值越大,
∵,,为二次函数图象上的三点,,
∴.
故选:B.
2.A
【分析】本题考查反比例函数与正比例函数图像交点问题,根据反比例函数与正比例函数相交于点,得到反比例函数与正比例函数的解析式,再联立方程组求解,即可得到点坐标.
【详解】解:∵反比例函数与正比例函数相交于点,
∴点在反比例函数与正比例函数图像上,满足函数解析式,
∴将代入到,得到;
同理将代入到,得到,
联立方程组
解得,,.
故选:A
3.D
【分析】本题主要考查了的几何意义,用表示三角形的面积是本题的解题关键.
【详解】解:的面积为,
.
故选:D.
4.D
【分析】本题考查了反比例函数的图像与性质,由于点不一定在同一象限,所以无法判断出的大小.
【详解】∵,
∴双曲线在第二、四象限,
①当时,;
②当时,;
③当时,;
综上,无法判断出的大小,
故选:D.
5.C
【分析】本题考查了二次函数综合问题;根据,有,可设点、的坐标为,代入解析式,即可解得答案.
【详解】解:,则是等腰直角三角形
,
可设点、的坐标为,
把代入,得
即,
,
,即.
故选:C.
6.A
【分析】本题考查了反比例函数图象上点的坐标特征,一次函数图象上点的坐标特征,二次函数函数图象上点的坐标特征,根据它们的坐标特征判断即可.
【详解】解:A、抛物线经过点,故符合题意;
B、双曲线不经过点,故不符合题意;
C、抛物线不经过点,故不符合题意;
D、直线不经过点,故不符合题意;
故选:A.
7.A
【分析】本题主要考查反比例函数图象的特点,熟练掌握反比例函数的图象的特点是解决本题的关键.根据偶次方的非负性,得,再根据反比例函数的图象的特点解决此题.
【详解】解:,
.
反比例函数为常数)的函数图象在第一、第三象限;在第一象限内,随着的增大而减小;在第三象限内,随着的增大而减小.
,
,,即.
故选:A
8.A
【分析】根据“上加下减,左加右减”的原则进行解答即可.此题考查了二次函数图象的平移与几何变换,利用抛物线解析式的变化规律:左加右减,上加下减是解题关键.
【详解】解:将将抛物线向左平移3个单位长度所得抛物线解析式为:,即;
再向下平移2个单位为:,即,
故选:A.
9.D
【分析】本题考查了函数的图象和函数关系式,理解题意是解题的关键.根据每个选项的意义,找出它们之间的函数关系,逐一判断.
【详解】解:A.汽车从甲地匀速行驶到乙地,剩余路程是行驶时间的一次函数,图象应该是线段,故A不符合题意;
B.当电压一定时,通过某用电器的电流与该用电器的电阻成反比例关系,图象应该是双曲线的一支,故B不符合题意;
C.圆锥的母线长等于底面圆的直径,其侧面积与底面圆的半径成二次函数关系,开口向上,故C不符合题意;
D.用长度一定的铁丝围成一个矩形,矩形的面积与一边长成二次函数关系,开口向下,故D符合题意;
故选:D.
10.A
【分析】本题考查了抛物线与x轴的交点,先求出抛物线的对称轴,在求出抛物线与x轴的另一个交点,最后根据抛物线与一元二次方程的关系求解.
【详解】解:∵抛物线的对称轴为:,图象与x轴的一个交点坐标是,
∴根据抛物线的对称性得抛物线与x轴的另一个交点是,
∴关于x的一元二次方程的两个实数根是:,,
故选:A.
11.①②④
【分析】先由证明,得出,再由勾股定理即可得出,从而判断①;设,,先由三角形的面积公式得出,,再根据二次函数的性质即可判断②;由勾股定理得到的表达式,利用二次函数性质求得最小值为,而,所以,从而③错误;如果四边形为平行四边形,则与互相平分,此时,,又为中点,所以当、分别为、的中点时,与互相平分,从而判断④.
【详解】解:中,,点为中点,
,,
,
,
.
在与中,
,
,
,
在中,.
故①正确;
设,,则.
,
当时,有最大值,
又,
.
故②正确;
,
当时,取得最小值,
(等号当且仅当时成立),
而,
.
故③错误;
当、分别为、的中点时,
∵,点D为的中点,
∴,
∵、分别为、的中点
∴,,
∴
∴四边形为正方形,此时与互相平分.
故④正确.
综上所述,正确的有:①②④.
故答案为:①②④.
【点睛】本题主要考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,三角形的面积,二次函数的性质等知识,综合性较强,有一定难度.
12.①③④
【分析】本题主要考查了二次函数的图象和性质,①由抛物线的开口方向、与y轴的交点判定a、c的符号;②将代入函数关系式,结合图象判定y的符号;③根据二次函数图象与x轴的交点解答;④利用二次函数图象与x轴的交点可得,再由,可作出判断.
【详解】解:观察函数图象得:抛物线开口向上,且与y轴交于负半轴,
∴,
∴,故①正确;
根据抛物线的图象得:该抛物线的对称轴是直线,
∴当时,,
即;故②错误;
③∵的图象与x轴的交点坐标分别为,
∴方程的根为,,故③正确;
∵的图象与x轴的交点坐标分别为,
∴,
∴,
观察图象得:,
∴,
∴,故④正确;
故答案为:①③④.
13.
【分析】本题考查的是比较二次函数的函数值的大小,选择合适的方法比较函数值的大小是解本题的关键,本题把点的坐标代入函数解析式先计算,再比较即可.
【详解】解:把点,代入,
∴,,
∴,
故答案为:
14.2
【分析】求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数的绝对值是较小的整数时,用配方法较好.
本题考查二次函数最大(小)值的求法.先用含的代数式表示出、再根据三角形的面积公式计算.
【详解】解:根据题意得,
三角形面积为:
∴当时,的面积最大为,
故答案为:2.
15.3
【分析】本题考查了反比例函数的比例系数的几何意义、与中线有关的三角形的面积,熟记反比例函数的比例系数的几何意义是解题的关键.连接,先求出,再根据反比例函数的比例系数的几何意义求解即可得.
【详解】解:如图,连接,
是线段的中点,的面积为3,
,
由反比例函数的图象可知,,
在反比例函数的图象,
,
解得,
故答案为:3.
16.
【分析】本题考查反比例函数系数的几何意义,根据反比例函数的的几何意义即可直接求解.
【详解】当在第一象限或第三象限时,,
当在第二象限或第四象限时,.
故答案是:.
17.(1);
(2)每件商品的销售价定为160元,商场日盈利最大,最大利润为1600元
【分析】本题考查二次函数的应用,关键是根据等量关系列出函数解析式和掌握二次函数的性质.
(1)根据每天可销售=涨价前每天可销售量-涨价减小的销售量,总利润单件利润销售数量,列出函数解析式即可;
(2)根据日盈利每件利润销售数量列出函数关系式,根据函数的性质求最值.
【详解】(1)解:由题意,得
即,
∴
即
(2)解:∵,
,
当时,有最大值,最大值为1600,
每件商品的销售价定为160元,商场日盈利最大,最大利润为1600元.
18.(1)
(2)
(3)
【分析】本题主要考查二次函数的应用,熟练掌握二次函数的图像和性质是解题的关键.
(1)根据二次函数与轴的交点得出点坐标,即可得到答案.
(2)求出第二次弹起的高度以及水平距离,根据函数图形的性质即可求出答案;
(3)求出的垂直距离即可得到答案.
【详解】(1)解:,
当时,,
解得,
;
(2)解:每次弹起的高度都是之前下落高度的,且水平方向飞行的距离也是原来的,
第一次弹起的高度为,水平距离
故第二次弹起的高度为,水平距离,
故第二次函数图像解析式为
时,
解得或,
故;
(3)解:由题意知第三次下落的高度为,
故第三次弹起的高度为,
故点的垂直距离为,
故与的高度差为.
答案第1页,共2页
答案第1页,共2页
