2023-2024学年沪科版八年级上册数学12.2 一次函数 第5课时 课件(共23张PPT)
文档属性
| 名称 | 2023-2024学年沪科版八年级上册数学12.2 一次函数 第5课时 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 235.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 07:09:20 | ||
图片预览






文档简介
(共23张PPT)
第十二章 一次函数
12.2 一次函数
第5课时 分段函数
1.知道在实际问题的应用中,可用表达式刻画两个变量间的关系.
2.了解分段函数的概念、特点及意义.
3.理解分段函数在自变量不同取值范围内的实际意义,并能解决相关实际问题.
一、学习目标
二、新课导入
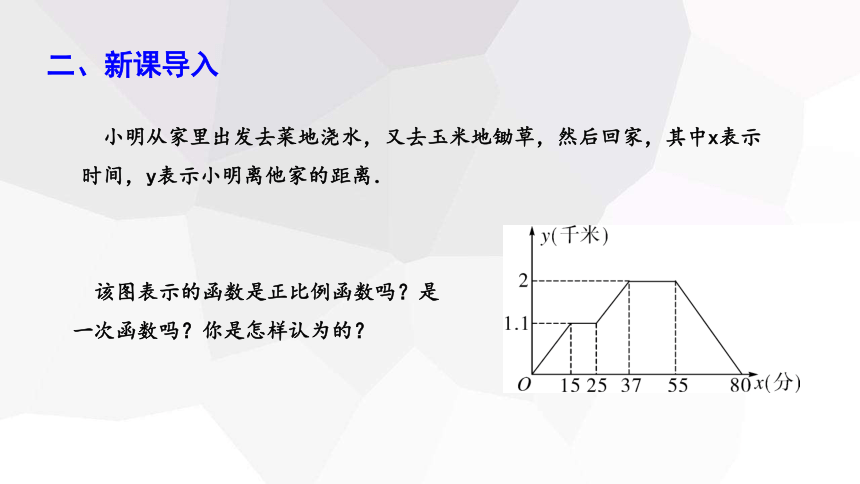
小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.
该图表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?
三、概念剖析
(一)分段函数
分段函数在生活中也有很多应用.
在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数.
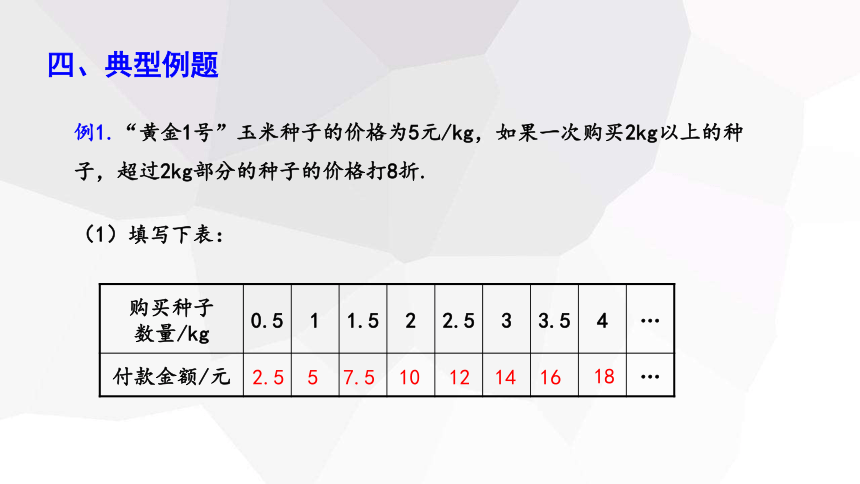
例1.“黄金1号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.
四、典型例题
(1)填写下表:
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
2.5
5
7.5
10
12
14
16
18
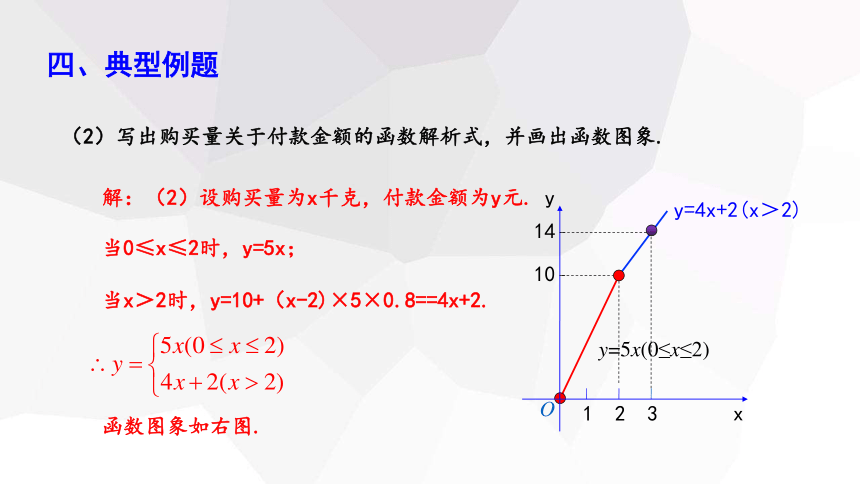
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
四、典型例题
解:(2)设购买量为x千克,付款金额为y元.
当0≤x≤2时,y=5x;
当x>2时,y=10+(x-2)×5×0.8==4x+2.
函数图象如右图.
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
总结:
从题目可知,种子的价格与购买种子量有关.种子量在不同的取值范围,所对应的函数关系式不同,这样的函数叫做分段函数.
四、典型例题
注意:1.分段函数是一个函数;2.每一段分段函数后面必须写明自变量的取值范围.
【当堂检测】
解析:复印超过100面的部分,每面收费(70-50)÷(150-100)=0.4元
1.下图是某复印店复印收费y(元)与复印面数(8开纸)x面的函数图象,从图象可以看出,复印超过100面的部分,每面收费( )
A. 0.4元 B. 0.45元
C. 约0.47元 D. 0.5元
A
【当堂检测】
2.某通讯公司的上网套餐每月上网费用y(单位:元)与上网流量x(单位:兆)的函数关系的图象如图所示.若该公司用户月上网流量超过500兆以后,每兆流量的费用为0.29元,则图中a的值为 .
解:该公司用户月上网流量超过500兆以后,每兆流量的费用为0.29元,由图象可得:
a=30+0.29×(600-500)=59元.
59
【当堂检测】
3.某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
解:(1)观察图象可知,当参加旅游的人数不超过10人时,人均收费240元.
240
【当堂检测】
答:参加这次旅游的人数是20人.
(2)如果该公司支付给旅行社的费用为人均180元,那么参加这次旅游的人数是多少?
解:(2)由题意得,参加这次旅游的人数在BC段.
设BC段的解析式是y=kx+b,根据图象可得
当y=180元时,则有180=-6x+300,解得x=20
解得 ,∴线段BC的解析式是y=-6x+300
例2.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过8立方米时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数关系式;
四、典型例题
分析:用水以8立方米为界,分成两段,收费标准不一样:当x≤8时,每立方米收费(1+0.3)元;当x>8时,超出部分每立方米收费(1.5+1.2)元.另外,收费时x一般取整数,不足1立方米的可并入下月计费.
解:(1)y关于x的函数关系式为
(2)画出上述函数图象;
四、典型例题
分析:依据函数表达式描出三个特殊点(0,0),(8,10.4)和(16,32)即可.
解:(2)函数图像如右图.
30
20
10
8
16
O
.
.
(8,10.4)
(16,32)
y/元
x/m3
(3)该市某户某月若用水x=5立方米或x=10立方米时,求应缴水费;
四、典型例题
即当用水量为5立方米时,该户应缴水费6.5元;当用水量为10立方米时,该户应缴水费15.8元.
解:(3)当x=5立方米时,y=1.3×5=6.5(元);当x=10立方米时,y=2.7×10-11.2=15.8(元).
分析:把x代入相应的关系式即可.
(4)该市某户某月缴水费26.6元,求该户这月用水量.
四、典型例题
即该户本月用水量为14 m3.
因此,2.7x-11.2=26.6,
分析:已知y的值求自变量x.
解:(4)y=26.6>1.3×8,可知该户这月用水超过8m3,
解方程,得 x=14.
四、典型例题
2.根据函数图象的性质和图象上的数据分析得出函数的类型,结合实际得出正确结论.
总结:
分段函数
1.读分段函数的图象时首先要理解横纵坐标表示的含义,自变量不同的取值范围所对应的函数表达式不同.
【当堂检测】
4.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药,
(1)服药后____小时,血液中含药量最高,达到每毫升_____毫克;
(2)服药5小时,血液中含药量为每毫升 毫克;
2
x/时
y/毫克
6
3
2
5
O
6
3
解析:(1)(2)观察函数图象可得出答案.
【当堂检测】
解:(3)由函数图象可得,当0≤x≤2时,可设y与x之间的函数关系式为y=kx,2k=6,解得k=3,
即当0≤x≤2时,y与x之间的函数关系式是y=3x
(3)当0≤x≤2时, y与x之间的函数关系式是__ ___;
x/时
y/毫克
6
3
2
5
O
【当堂检测】
(4)当x≥2时, y与x之间的函数关系式是_________;
x/时
y/毫克
6
3
2
5
O
即当≥2时,y与x之间的函数关系式是y=-x+8
解:(4)由函数图象可得,当x≥2时,设y与x之间的函数关系式为y=kx+b,则有 ,解得
【当堂检测】
解:(5)将y=3代入y=3x中,得x=1,
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,
那么这个有效时间是 小时.
由图象可知,当x=5时,y=3,
因此,当1≤x≤5时,y≥3,即每毫升血液中含药量在3毫克或3毫克以上.故答案为1≤x≤5.
x/时
y/毫克
6
3
2
5
O
【当堂检测】
5.“五一”黄金周的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
(1)小明全家在旅游景点游玩了多少小时?
解:(1)由图象可知,小明全家在旅游景点游玩了4小时.
5
10
15
120
180
s(千米)
t(时)
O
A
B
C
D
8
14
【当堂检测】
(2)求返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家是什么时间?
5
10
15
120
180
s(千米)
t(时)
O
A
B
C
D
8
14
解:(2)设s=kt+b,由图象过(14,180)、(15,120)可得,
∴S=-60t+1020 .
令S=0,得t=17.
∴返程途中s与时间t的函数关系是s=-60t+1020(14≤x≤17),故小明全家当天17:00到家.
五、课堂总结
1.分段函数是一个函数,而不是几个函数.
分段函数
2.自变量在不同的取值范围内,函数表达式不同,函数图象也不同.
3.分段函数的实际应用
第十二章 一次函数
12.2 一次函数
第5课时 分段函数
1.知道在实际问题的应用中,可用表达式刻画两个变量间的关系.
2.了解分段函数的概念、特点及意义.
3.理解分段函数在自变量不同取值范围内的实际意义,并能解决相关实际问题.
一、学习目标
二、新课导入
小明从家里出发去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.
该图表示的函数是正比例函数吗?是一次函数吗?你是怎样认为的?
三、概念剖析
(一)分段函数
分段函数在生活中也有很多应用.
在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数.
例1.“黄金1号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.
四、典型例题
(1)填写下表:
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
2.5
5
7.5
10
12
14
16
18
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
四、典型例题
解:(2)设购买量为x千克,付款金额为y元.
当0≤x≤2时,y=5x;
当x>2时,y=10+(x-2)×5×0.8==4x+2.
函数图象如右图.
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
总结:
从题目可知,种子的价格与购买种子量有关.种子量在不同的取值范围,所对应的函数关系式不同,这样的函数叫做分段函数.
四、典型例题
注意:1.分段函数是一个函数;2.每一段分段函数后面必须写明自变量的取值范围.
【当堂检测】
解析:复印超过100面的部分,每面收费(70-50)÷(150-100)=0.4元
1.下图是某复印店复印收费y(元)与复印面数(8开纸)x面的函数图象,从图象可以看出,复印超过100面的部分,每面收费( )
A. 0.4元 B. 0.45元
C. 约0.47元 D. 0.5元
A
【当堂检测】
2.某通讯公司的上网套餐每月上网费用y(单位:元)与上网流量x(单位:兆)的函数关系的图象如图所示.若该公司用户月上网流量超过500兆以后,每兆流量的费用为0.29元,则图中a的值为 .
解:该公司用户月上网流量超过500兆以后,每兆流量的费用为0.29元,由图象可得:
a=30+0.29×(600-500)=59元.
59
【当堂检测】
3.某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
解:(1)观察图象可知,当参加旅游的人数不超过10人时,人均收费240元.
240
【当堂检测】
答:参加这次旅游的人数是20人.
(2)如果该公司支付给旅行社的费用为人均180元,那么参加这次旅游的人数是多少?
解:(2)由题意得,参加这次旅游的人数在BC段.
设BC段的解析式是y=kx+b,根据图象可得
当y=180元时,则有180=-6x+300,解得x=20
解得 ,∴线段BC的解析式是y=-6x+300
例2.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过8立方米时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数关系式;
四、典型例题
分析:用水以8立方米为界,分成两段,收费标准不一样:当x≤8时,每立方米收费(1+0.3)元;当x>8时,超出部分每立方米收费(1.5+1.2)元.另外,收费时x一般取整数,不足1立方米的可并入下月计费.
解:(1)y关于x的函数关系式为
(2)画出上述函数图象;
四、典型例题
分析:依据函数表达式描出三个特殊点(0,0),(8,10.4)和(16,32)即可.
解:(2)函数图像如右图.
30
20
10
8
16
O
.
.
(8,10.4)
(16,32)
y/元
x/m3
(3)该市某户某月若用水x=5立方米或x=10立方米时,求应缴水费;
四、典型例题
即当用水量为5立方米时,该户应缴水费6.5元;当用水量为10立方米时,该户应缴水费15.8元.
解:(3)当x=5立方米时,y=1.3×5=6.5(元);当x=10立方米时,y=2.7×10-11.2=15.8(元).
分析:把x代入相应的关系式即可.
(4)该市某户某月缴水费26.6元,求该户这月用水量.
四、典型例题
即该户本月用水量为14 m3.
因此,2.7x-11.2=26.6,
分析:已知y的值求自变量x.
解:(4)y=26.6>1.3×8,可知该户这月用水超过8m3,
解方程,得 x=14.
四、典型例题
2.根据函数图象的性质和图象上的数据分析得出函数的类型,结合实际得出正确结论.
总结:
分段函数
1.读分段函数的图象时首先要理解横纵坐标表示的含义,自变量不同的取值范围所对应的函数表达式不同.
【当堂检测】
4.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药,
(1)服药后____小时,血液中含药量最高,达到每毫升_____毫克;
(2)服药5小时,血液中含药量为每毫升 毫克;
2
x/时
y/毫克
6
3
2
5
O
6
3
解析:(1)(2)观察函数图象可得出答案.
【当堂检测】
解:(3)由函数图象可得,当0≤x≤2时,可设y与x之间的函数关系式为y=kx,2k=6,解得k=3,
即当0≤x≤2时,y与x之间的函数关系式是y=3x
(3)当0≤x≤2时, y与x之间的函数关系式是__ ___;
x/时
y/毫克
6
3
2
5
O
【当堂检测】
(4)当x≥2时, y与x之间的函数关系式是_________;
x/时
y/毫克
6
3
2
5
O
即当≥2时,y与x之间的函数关系式是y=-x+8
解:(4)由函数图象可得,当x≥2时,设y与x之间的函数关系式为y=kx+b,则有 ,解得
【当堂检测】
解:(5)将y=3代入y=3x中,得x=1,
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,
那么这个有效时间是 小时.
由图象可知,当x=5时,y=3,
因此,当1≤x≤5时,y≥3,即每毫升血液中含药量在3毫克或3毫克以上.故答案为1≤x≤5.
x/时
y/毫克
6
3
2
5
O
【当堂检测】
5.“五一”黄金周的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
(1)小明全家在旅游景点游玩了多少小时?
解:(1)由图象可知,小明全家在旅游景点游玩了4小时.
5
10
15
120
180
s(千米)
t(时)
O
A
B
C
D
8
14
【当堂检测】
(2)求返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家是什么时间?
5
10
15
120
180
s(千米)
t(时)
O
A
B
C
D
8
14
解:(2)设s=kt+b,由图象过(14,180)、(15,120)可得,
∴S=-60t+1020 .
令S=0,得t=17.
∴返程途中s与时间t的函数关系是s=-60t+1020(14≤x≤17),故小明全家当天17:00到家.
五、课堂总结
1.分段函数是一个函数,而不是几个函数.
分段函数
2.自变量在不同的取值范围内,函数表达式不同,函数图象也不同.
3.分段函数的实际应用
