12.1 函数 第4课时 课件(共18张PPT)2023-2024学年沪科版八年级上册数学
文档属性
| 名称 | 12.1 函数 第4课时 课件(共18张PPT)2023-2024学年沪科版八年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 284.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 07:10:02 | ||
图片预览






文档简介
(共18张PPT)
第十二章 一次函数
12.1 函数
第4课时 从函数图像中获取信息
1.能从函数图象中获取与函数有关的信息,解决函数中的问题
2.能通过函数间变量的关系,理解图象中的点或线段代表的实际意义
3.体会数形结合思想,提高解决问题的能力
一、学习目标
复习旧知
二、新课导入
由函数表达式画图象的一般步骤:
1.列表
2.描点
3.连线
二、新课导入
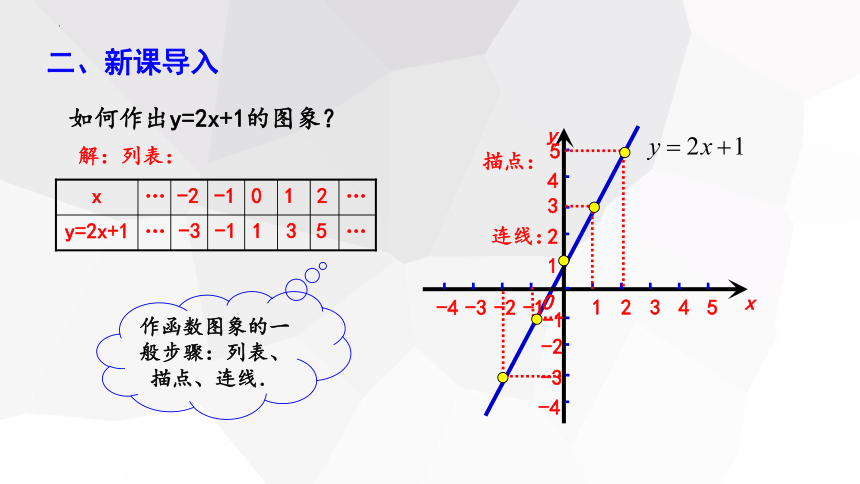
如何作出y=2x+1的图象?
解:列表:
…
…
y=2x+1
…
2
1
0
-1
-2
…
x
-3
-1
1
5
3
连线:
描点:
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
作函数图象的一般步骤:列表、描点、连线.
(一)从函数图形中获取信息
三、概念剖析
函数关系用图像表示,直观、形象,容易从中了解函数的一些变化情况.
横轴表示自变量,纵轴是因变量.
最高点表示因变量的最大值,最低点表示因变量的最小值.
(一)从函数图形中获取信息
三、概念剖析
水平线部分表示函数在相应区间内函数值不变.
函数关系用图像表示,直观、形象,容易从中了解函数的一些变化情况.
例1.张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店买笔,然后走回家,如图是张阳离家的距离与时间的关系图像.根据图像回答下列问题:
四、典型例题
(1)在这个变化过程中,自变量、因变量分别是 、 .
时间
距离
解析:(1)在这个变化中,自变量、因变量分别是时间、距离.
四、典型例题
2.5
1
(2)体育场离张阳家 千米,体育场离文具店 千米.
解析:(2)体育场离张阳家2.5千米,体育场离文具店2.5-1.5=1千米.
例1.张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店买笔,然后走回家,如图是张阳离家的距离与时间的关系图像.根据图像回答下列问题:
四、典型例题
(3)张阳在文具店逗留了 时间,他从文具店到家的速度是 .
20分钟
米/分钟
解析:(3)张阳在文具店逗留了65-45=20分钟,张阳从文具店到家的速度是 米/分钟.
例1.张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店买笔,然后走回家,如图是张阳离家的距离与时间的关系图像.根据图像回答下列问题:
总结:
四、典型例题
(1)根据函数的概念解答即可.
(2)观察函数图像的纵坐标,可得因变量y;观察函数图像的横坐标,可得自变量x.
1.甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
A.前2分钟,乙的平均速度比甲快
B.5分钟两人都跑了500米
C.甲跑完800米的平均速度为100米/分
D.甲乙两人8分钟各跑了800米
D
【当堂检测】
解:由图可得,甲8分钟跑了800米,乙8分钟跑了700米.
2.小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图像是( )
A. B. C. D.
B
【当堂检测】
解:由题可得,相同的路程,跑步比慢步的速度快.在一定时间内没有移动距离,则速度为0.
例2.甲乙两人从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离s(单位:km)和行驶时间t(单位:h)之间的关系的图像如图所示,已知甲停止一段时间后再次行走的速度是原来的一半,回答下列问题:
(1)求乙的速度.
四、典型例题
解:(1)根据图像,可得乙的速度为
(km/h)
例2.甲乙两人从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离s(单位:km)和行驶时间t(单位:h)之间的关系的图像如图所示,已知甲停止一段时间后再次行走的速度是原来的一半,回答下列问题:
(2)甲中途停止了多长时间?
四、典型例题
解:(2)甲原来的速度为 (km/h)
甲后来的速度为 (km/h),
由题意得 ,解得a=1,
则a-0.5=1-0.5=0.5,故甲中途停止了0.5小时.
(3)两人相遇时,离B地的路程是多少千米?
四、典型例题
解:(3)
乙离A地的路程为
他们离B地的路程是20-10=10(km)
总结:
四、典型例题
(3)读图分析函数图像最高点、最低点分别表示的意义
(4)观察函数图像,体会数形结合思想
3.如图所示的函数图像反映如下过程:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离家的距离,读图可知菜地离小徐家的距离为( )
A. 1.1千米 B. 2千米
C. 15千米 D. 37千米
A
【当堂检测】
解:由图像可以看出菜地离小徐家1.1千米.
五、课堂总结
从函数图像中获取信息
(1)横轴表示自变量,纵轴是因变量.
(2)最高点表示因变量的最大值,最低点表示因变量的最小值.
(3)不同区间表示的函数意义不同.
第十二章 一次函数
12.1 函数
第4课时 从函数图像中获取信息
1.能从函数图象中获取与函数有关的信息,解决函数中的问题
2.能通过函数间变量的关系,理解图象中的点或线段代表的实际意义
3.体会数形结合思想,提高解决问题的能力
一、学习目标
复习旧知
二、新课导入
由函数表达式画图象的一般步骤:
1.列表
2.描点
3.连线
二、新课导入
如何作出y=2x+1的图象?
解:列表:
…
…
y=2x+1
…
2
1
0
-1
-2
…
x
-3
-1
1
5
3
连线:
描点:
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
作函数图象的一般步骤:列表、描点、连线.
(一)从函数图形中获取信息
三、概念剖析
函数关系用图像表示,直观、形象,容易从中了解函数的一些变化情况.
横轴表示自变量,纵轴是因变量.
最高点表示因变量的最大值,最低点表示因变量的最小值.
(一)从函数图形中获取信息
三、概念剖析
水平线部分表示函数在相应区间内函数值不变.
函数关系用图像表示,直观、形象,容易从中了解函数的一些变化情况.
例1.张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店买笔,然后走回家,如图是张阳离家的距离与时间的关系图像.根据图像回答下列问题:
四、典型例题
(1)在这个变化过程中,自变量、因变量分别是 、 .
时间
距离
解析:(1)在这个变化中,自变量、因变量分别是时间、距离.
四、典型例题
2.5
1
(2)体育场离张阳家 千米,体育场离文具店 千米.
解析:(2)体育场离张阳家2.5千米,体育场离文具店2.5-1.5=1千米.
例1.张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店买笔,然后走回家,如图是张阳离家的距离与时间的关系图像.根据图像回答下列问题:
四、典型例题
(3)张阳在文具店逗留了 时间,他从文具店到家的速度是 .
20分钟
米/分钟
解析:(3)张阳在文具店逗留了65-45=20分钟,张阳从文具店到家的速度是 米/分钟.
例1.张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店买笔,然后走回家,如图是张阳离家的距离与时间的关系图像.根据图像回答下列问题:
总结:
四、典型例题
(1)根据函数的概念解答即可.
(2)观察函数图像的纵坐标,可得因变量y;观察函数图像的横坐标,可得自变量x.
1.甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
A.前2分钟,乙的平均速度比甲快
B.5分钟两人都跑了500米
C.甲跑完800米的平均速度为100米/分
D.甲乙两人8分钟各跑了800米
D
【当堂检测】
解:由图可得,甲8分钟跑了800米,乙8分钟跑了700米.
2.小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图像是( )
A. B. C. D.
B
【当堂检测】
解:由题可得,相同的路程,跑步比慢步的速度快.在一定时间内没有移动距离,则速度为0.
例2.甲乙两人从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离s(单位:km)和行驶时间t(单位:h)之间的关系的图像如图所示,已知甲停止一段时间后再次行走的速度是原来的一半,回答下列问题:
(1)求乙的速度.
四、典型例题
解:(1)根据图像,可得乙的速度为
(km/h)
例2.甲乙两人从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离s(单位:km)和行驶时间t(单位:h)之间的关系的图像如图所示,已知甲停止一段时间后再次行走的速度是原来的一半,回答下列问题:
(2)甲中途停止了多长时间?
四、典型例题
解:(2)甲原来的速度为 (km/h)
甲后来的速度为 (km/h),
由题意得 ,解得a=1,
则a-0.5=1-0.5=0.5,故甲中途停止了0.5小时.
(3)两人相遇时,离B地的路程是多少千米?
四、典型例题
解:(3)
乙离A地的路程为
他们离B地的路程是20-10=10(km)
总结:
四、典型例题
(3)读图分析函数图像最高点、最低点分别表示的意义
(4)观察函数图像,体会数形结合思想
3.如图所示的函数图像反映如下过程:小徐从家去菜地浇水,又去玉米地除草,然后回家.其中x表示时间,y表示小徐离家的距离,读图可知菜地离小徐家的距离为( )
A. 1.1千米 B. 2千米
C. 15千米 D. 37千米
A
【当堂检测】
解:由图像可以看出菜地离小徐家1.1千米.
五、课堂总结
从函数图像中获取信息
(1)横轴表示自变量,纵轴是因变量.
(2)最高点表示因变量的最大值,最低点表示因变量的最小值.
(3)不同区间表示的函数意义不同.
