2023-2024学年沪科版八年级上册数学12.1 函数 第1课时 课件(共17张PPT)
文档属性
| 名称 | 2023-2024学年沪科版八年级上册数学12.1 函数 第1课时 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 07:12:07 | ||
图片预览






文档简介
(共17张PPT)
第十二章 一次函数
12.1 函数
12.1.1 函数的相关概念
1.通过实例,理解常量、变量的意义.
2.能判别实际问题中出现的常量、变量与自变量.
3.了解函数的意义,能说出生活中的一些函数实例.
一、学习目标
二、新课导入
如图是一个圆形,若用S表示它的面积,用r表示半径,如何表示它的面积公式?
r
r
三、概念剖析
1.思考:在“新课导入”中:可将圆的面积可以表示为S=πr2 ,当r=1,
r=2时,它的面积是多少?
当r=1,r=2时,它的面积分别是S=π,S=4π.
圆的面积公式S=πr2
中不变的量是?
(一)变量与常量
π
三、概念剖析
2.变量与常量的概念
在某一变化过程中,称数值发生变化的量为变量,始终不变的量称为常量.
(一)变量与常量
三、概念剖析
(二)函数与自变量
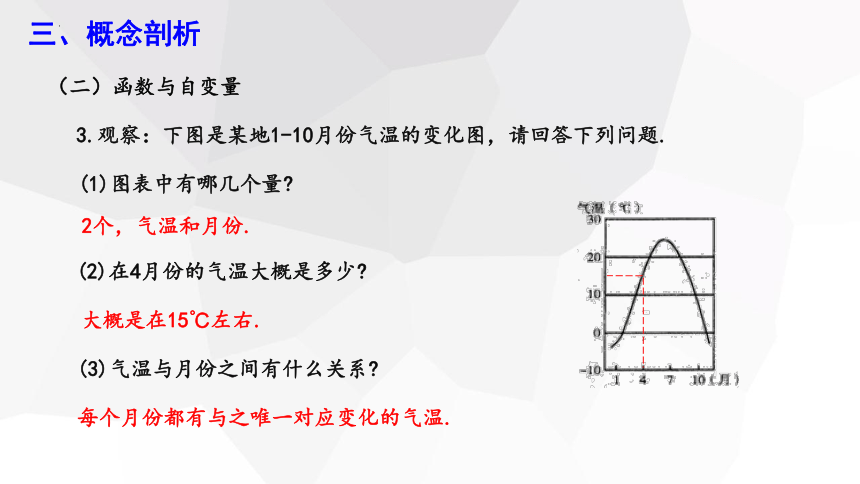
3.观察:下图是某地1-10月份气温的变化图,请回答下列问题.
(1)图表中有哪几个量
(2)在4月份的气温大概是多少
2个,气温和月份.
大概是在15℃左右.
(3)气温与月份之间有什么关系
每个月份都有与之唯一对应变化的气温.
三、概念剖析
4.函数与自变量的相关概念
(二)函数与自变量
一般地,设在一个变化过程中有两个变量x与y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值与它对应,那么就说x是自变量,y是x的函数.
三、概念剖析
5.讨论:在上面的几个问题中,每个变化过程都涉及两个变量,说一说哪些变量是引发变化过程的“原因”.
(二)函数与自变量
引发变化过程的“原因”分别是圆的半径r和月份.
三、概念剖析
(二)函数与自变量
结论:上面的几个问题中,每个变化过程中都有两个变量,他们之间存在某种对应关系,当其中一个变量变化(我们叫它自变量),相应地就有确定的另一个量跟着唯一变化(我们叫它因变量).
四、典型例题
例1.根据题意回答问题,指出下列关系式中的变量与常量:
解:变量是:S;R
常量是:4π.
(2)小明购买单价是2.5元的圆珠笔,请写出总金额y元与圆珠笔数n支的关系.
解:关系式是y=2.5n
其中常量是2.5,自变量n,因变量是y.
(1)球的表面积Scm2与球的半径Rcm的关系式是:S=4πR2.
四、典型例题
解:判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量是否有唯一确定的值与它对应.因此可判断出①,②,③正确.
①,②,③
四、典型例题
注意:在做题中不能忽略在分式中,分母不能为0的情况.
(2)求当x取什么值时,函数的值为0.
【当堂检测】
1.在△ABC中,它的底边是a,底边上的高是h,则三角形的面积S=0.5ah,当a为定长时,在此式中( )
A.S、h是变量,0.5、a是常量 B.S、h、a是变量,0.5是常量
C.a、h是变量,0.5、S是常量 D.S是变量,0.5、a、h是常量
A
解:根据常量和变量的定义可判断:a为定长时,a是常量,S、h是变量,故选A.
【当堂检测】
2.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是 .
解:因为汽车是匀速行驶的,因此①速度是常量,不会发生变化,而行驶时间,行驶路程,剩余油量会发生变化,所以②行驶时间;③行驶路程;④汽车油箱中的剩余油量是变量.故变量的个数是3个.
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
3个
【当堂检测】
3.有下列说法:
上述说法中正确的是?请写出他们的函数关系式.
①若y<2x,则y是x的函数;②正方形面积是周长的函数;
③变量x,y满足y2=2x,y是x的函数; ④温度是变量.
【当堂检测】
4.写出下列各问题的函数关系式,并指出其中的常量与变量,自变量与函数.
(2)正n边形的内角和C与边数n(n≥3,n取正整数)之间的关系式.
(1)运动员在200米一圈的跑道上训练,他跑一圈所用的时间t(秒)与跑步的速度v(米/秒)的关系式;
解:依题意得,C=180°(n-2) ,其中180°是常量,C、n是变量,n是自变量,
C是n的函数.
五、课堂总结
第十二章 一次函数
12.1 函数
12.1.1 函数的相关概念
1.通过实例,理解常量、变量的意义.
2.能判别实际问题中出现的常量、变量与自变量.
3.了解函数的意义,能说出生活中的一些函数实例.
一、学习目标
二、新课导入
如图是一个圆形,若用S表示它的面积,用r表示半径,如何表示它的面积公式?
r
r
三、概念剖析
1.思考:在“新课导入”中:可将圆的面积可以表示为S=πr2 ,当r=1,
r=2时,它的面积是多少?
当r=1,r=2时,它的面积分别是S=π,S=4π.
圆的面积公式S=πr2
中不变的量是?
(一)变量与常量
π
三、概念剖析
2.变量与常量的概念
在某一变化过程中,称数值发生变化的量为变量,始终不变的量称为常量.
(一)变量与常量
三、概念剖析
(二)函数与自变量
3.观察:下图是某地1-10月份气温的变化图,请回答下列问题.
(1)图表中有哪几个量
(2)在4月份的气温大概是多少
2个,气温和月份.
大概是在15℃左右.
(3)气温与月份之间有什么关系
每个月份都有与之唯一对应变化的气温.
三、概念剖析
4.函数与自变量的相关概念
(二)函数与自变量
一般地,设在一个变化过程中有两个变量x与y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值与它对应,那么就说x是自变量,y是x的函数.
三、概念剖析
5.讨论:在上面的几个问题中,每个变化过程都涉及两个变量,说一说哪些变量是引发变化过程的“原因”.
(二)函数与自变量
引发变化过程的“原因”分别是圆的半径r和月份.
三、概念剖析
(二)函数与自变量
结论:上面的几个问题中,每个变化过程中都有两个变量,他们之间存在某种对应关系,当其中一个变量变化(我们叫它自变量),相应地就有确定的另一个量跟着唯一变化(我们叫它因变量).
四、典型例题
例1.根据题意回答问题,指出下列关系式中的变量与常量:
解:变量是:S;R
常量是:4π.
(2)小明购买单价是2.5元的圆珠笔,请写出总金额y元与圆珠笔数n支的关系.
解:关系式是y=2.5n
其中常量是2.5,自变量n,因变量是y.
(1)球的表面积Scm2与球的半径Rcm的关系式是:S=4πR2.
四、典型例题
解:判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量是否有唯一确定的值与它对应.因此可判断出①,②,③正确.
①,②,③
四、典型例题
注意:在做题中不能忽略在分式中,分母不能为0的情况.
(2)求当x取什么值时,函数的值为0.
【当堂检测】
1.在△ABC中,它的底边是a,底边上的高是h,则三角形的面积S=0.5ah,当a为定长时,在此式中( )
A.S、h是变量,0.5、a是常量 B.S、h、a是变量,0.5是常量
C.a、h是变量,0.5、S是常量 D.S是变量,0.5、a、h是常量
A
解:根据常量和变量的定义可判断:a为定长时,a是常量,S、h是变量,故选A.
【当堂检测】
2.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是 .
解:因为汽车是匀速行驶的,因此①速度是常量,不会发生变化,而行驶时间,行驶路程,剩余油量会发生变化,所以②行驶时间;③行驶路程;④汽车油箱中的剩余油量是变量.故变量的个数是3个.
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
3个
【当堂检测】
3.有下列说法:
上述说法中正确的是?请写出他们的函数关系式.
①若y<2x,则y是x的函数;②正方形面积是周长的函数;
③变量x,y满足y2=2x,y是x的函数; ④温度是变量.
【当堂检测】
4.写出下列各问题的函数关系式,并指出其中的常量与变量,自变量与函数.
(2)正n边形的内角和C与边数n(n≥3,n取正整数)之间的关系式.
(1)运动员在200米一圈的跑道上训练,他跑一圈所用的时间t(秒)与跑步的速度v(米/秒)的关系式;
解:依题意得,C=180°(n-2) ,其中180°是常量,C、n是变量,n是自变量,
C是n的函数.
五、课堂总结
