2023-2024学年沪科版八年级上册数学12.1 函数 第2课时 课件(共20张PPT)
文档属性
| 名称 | 2023-2024学年沪科版八年级上册数学12.1 函数 第2课时 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 205.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 07:13:54 | ||
图片预览








文档简介
(共20张PPT)
第十二章 一次函数
12.1 函数
第2课时 函数的三种表示法
1.知道表示函数有三种方法,会用列表法、解析法表示函数关系
2.能根据实际问题的已知条件,列出简单的函数关系的表达式
3.会确定自变量的取值范围,会根据自变量求函数的值.
一、学习目标
二、新课导入
复习旧知
小兰一家自驾游,路程S是自变量时间t的函数;
一般地,设在一个变化过程中有两个变量x与y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值与它对应,那么我们就说x是自变量,y是x的函数.
嘉年华门票,门票总收入额y是自变量日人流量x的函数;
下列问题中的变量y是不是x的函数?
是
(1) y = 2x
(2) y+2x=3
是
(3) y=
不是
(6)
是
(7)
不是
(4) y=x2
(5) y2=x
(8) y=±x+5
(9) y=x2+3z
是
是
不是
不是
(x≥0)
二、新课导入
三、概念剖析
(一)函数的三种表示法
描述函数的方法有:① ;② ;③ .
列表法
关系式法
图像法
1. 列表法
定义:通过列出自变量的值与对应函数值的表格来表示函数关系的方法叫做列表法。
优点:不必计算就知道自变量取某些值时函数的对应值。
三、概念剖析
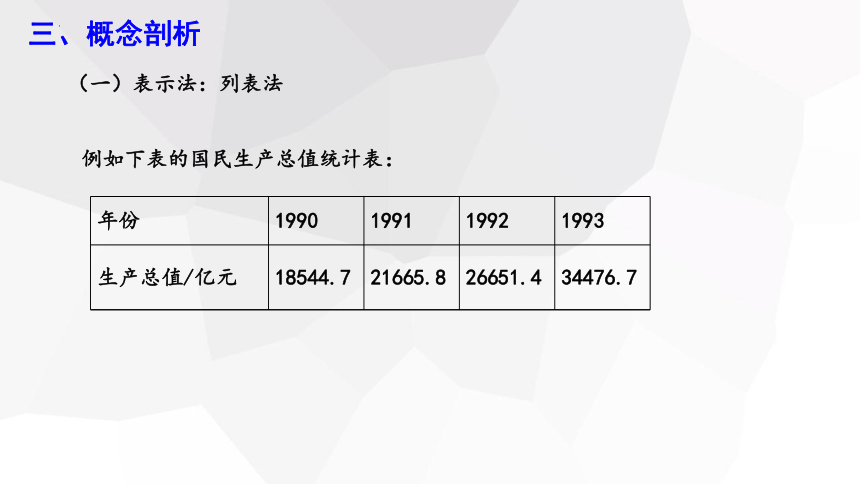
例如下表的国民生产总值统计表:
年份 1990 1991 1992 1993
生产总值/亿元 18544.7 21665.8 26651.4 34476.7
(一)表示法:列表法
(一)表示法:解析法
定义:用数学式子表示函数关系的方法叫做解析法 . 其中的等式叫做函数的解析式(或函数关系式).
例如:汽车在平整路面上的刹车距离s与车速v之间的函数关系是用数学式子 来表示的
优点:一是简明、全面的概括了变量间的关系,二是可以通过解析式求出任意一个自变量所对应的函数值.
三、概念剖析
列表法 解析法 图象法
定义 通过列出自变量的值,与对应函数值的表格来表示函数关系的方法 用数学式子表示函数关系的方法 用图象来表示两个变量间的函数关系的方法
优点 具体反映了函数随自变量的数值对应关系 准确地反映了函数随自变量的数量关系 直观地反映了函数随自变量的变化而变化的规律
三、概念剖析
(一)三种表示法优缺点
三、概念剖析
在用解析式表示函数时,要考虑自变量的取值范围必须使解析式有意义.
(二)自变量的取值范围
当函数解析式为分式时,其自变量的取值范围是分母不等于零的未知数的值.
当函数解析式为开方式时,自变量的取值应使被开方式大于等于零.
当函数解析式为综合算式时,函数的取值范围应使函数的各个部分都有意义.
与实际问题相关的函数自变量取值范围不仅要使解析式有意义,而且应使实际问题有意义.
三、概念剖析
在函数解析式中,以自变量的值代入求得的值叫做函数值.
(一)函数值
例1.当x=3时,求下列函数的函数值:
(1)y=2x+4
四、典型例题
四、典型例题
例2.求下列函数中自变量 x 的取值范围:
(1)x为全体实数.
(3)x-2≠0,即x≠2.
(2)x为全体实数.
(4)x-3≥0,即x≥3.
四、典型例题
例3.一个游泳池内有水300m ,现打开排水管以每小时25 m 的排水量排水。
(1)写出游泳池内剩余水量Q m 与排水时间t h的函数关系式;
(2)写出自变量t的取值范围;
(2)由于池中共有300m 水,每小时排25 m ,全部排完只需300÷25=12(h),故自变量的取值范围是0≤t≤12.
(1)排水后的剩水量Q是排水时间t的函数,有Q=300-25t=-25t+300.
四、典型例题
(3)当t=5,代入上式,得Q=-5×25+300=175m ,即第5h末,游泳池内还有水175 m .
(4)当Q=150时,由150=-25t+300,得t=6(h),即第6h末池中有水150 m .
(3)开始排水后的第5h末,游泳池内还有多少水?
(4)当游泳池中还剩150 m 时,已经排水多少小时?
【当堂检测】
1.求下列中函数x=2的函数值,并指出自变量的范围:
(1)y=-3x+2; (2)y =2x2;
(3)
解:(1)当x=2时,y=-3x+2=-3×2+2=-4,自变量取值范围为R;
(2)当x=2时,y =2x2=2×22=8,自变量取值范围为R;
(3)当x=2时, ,自变量取值范围为x≠2.5
【当堂检测】
2.已知x与y的关系式为y=x+1,当y为2时,x值为( )
A. 1 B. 2 C. 3 D. -1
解:将y=2代入关系式y=x+1得2=x+1,解得x=1,故选A.
A
【当堂检测】
3.函数的三种表示方法分别是( )
A. 坐标法;画图法;解析式法
B. 画图法;列表法,解析式法
C. 图像法;列表法;解析式法
D. 图像法;列表法; 关系式法
函数有三种表示方法——图像法、列表法、解析式法,故选C.
C
【当堂检测】
4.从甲地到乙地的路程为300千米,一辆汽车从甲地到乙地,每小时行驶50千米,行驶的时间为t(小时),离乙地的路程为s(千米),则下表剩余两空应填( )
解:行驶的时间为t与离乙地的路程为s的关系式为s=300-50t,将t=5和t=6分别代入关系式可求得对应s的值为50和0,故选B.
t(小时) 1 2 3 4 5 6
s(千米) 250 200 150 100
B
A. 100;50 B. 50;0 C. 50;25 D. 250;300
【当堂检测】
5.某学校举办活动需购买一些气球,这些气球单价均为0.5元一个,假设购买数量为x,购买气球所要花费的总金额为y,则y与x的关系式为( )
解:总金额=单价×购买数量,故y与x的关系式为y=0.5x,故选A.
A. y=0.5x B. y=2x C. y=x+0.5 D. y=x-0.5
A
函数的表示方法
列表法、解析法和图象法
自变量的取值范围
使含自变量的等式有意义
使实际问题有意义
用列表法、解析法表示函数关系
五、课堂总结
第十二章 一次函数
12.1 函数
第2课时 函数的三种表示法
1.知道表示函数有三种方法,会用列表法、解析法表示函数关系
2.能根据实际问题的已知条件,列出简单的函数关系的表达式
3.会确定自变量的取值范围,会根据自变量求函数的值.
一、学习目标
二、新课导入
复习旧知
小兰一家自驾游,路程S是自变量时间t的函数;
一般地,设在一个变化过程中有两个变量x与y,如果对于x在它允许取值范围内的每一个值,y都有唯一确定的值与它对应,那么我们就说x是自变量,y是x的函数.
嘉年华门票,门票总收入额y是自变量日人流量x的函数;
下列问题中的变量y是不是x的函数?
是
(1) y = 2x
(2) y+2x=3
是
(3) y=
不是
(6)
是
(7)
不是
(4) y=x2
(5) y2=x
(8) y=±x+5
(9) y=x2+3z
是
是
不是
不是
(x≥0)
二、新课导入
三、概念剖析
(一)函数的三种表示法
描述函数的方法有:① ;② ;③ .
列表法
关系式法
图像法
1. 列表法
定义:通过列出自变量的值与对应函数值的表格来表示函数关系的方法叫做列表法。
优点:不必计算就知道自变量取某些值时函数的对应值。
三、概念剖析
例如下表的国民生产总值统计表:
年份 1990 1991 1992 1993
生产总值/亿元 18544.7 21665.8 26651.4 34476.7
(一)表示法:列表法
(一)表示法:解析法
定义:用数学式子表示函数关系的方法叫做解析法 . 其中的等式叫做函数的解析式(或函数关系式).
例如:汽车在平整路面上的刹车距离s与车速v之间的函数关系是用数学式子 来表示的
优点:一是简明、全面的概括了变量间的关系,二是可以通过解析式求出任意一个自变量所对应的函数值.
三、概念剖析
列表法 解析法 图象法
定义 通过列出自变量的值,与对应函数值的表格来表示函数关系的方法 用数学式子表示函数关系的方法 用图象来表示两个变量间的函数关系的方法
优点 具体反映了函数随自变量的数值对应关系 准确地反映了函数随自变量的数量关系 直观地反映了函数随自变量的变化而变化的规律
三、概念剖析
(一)三种表示法优缺点
三、概念剖析
在用解析式表示函数时,要考虑自变量的取值范围必须使解析式有意义.
(二)自变量的取值范围
当函数解析式为分式时,其自变量的取值范围是分母不等于零的未知数的值.
当函数解析式为开方式时,自变量的取值应使被开方式大于等于零.
当函数解析式为综合算式时,函数的取值范围应使函数的各个部分都有意义.
与实际问题相关的函数自变量取值范围不仅要使解析式有意义,而且应使实际问题有意义.
三、概念剖析
在函数解析式中,以自变量的值代入求得的值叫做函数值.
(一)函数值
例1.当x=3时,求下列函数的函数值:
(1)y=2x+4
四、典型例题
四、典型例题
例2.求下列函数中自变量 x 的取值范围:
(1)x为全体实数.
(3)x-2≠0,即x≠2.
(2)x为全体实数.
(4)x-3≥0,即x≥3.
四、典型例题
例3.一个游泳池内有水300m ,现打开排水管以每小时25 m 的排水量排水。
(1)写出游泳池内剩余水量Q m 与排水时间t h的函数关系式;
(2)写出自变量t的取值范围;
(2)由于池中共有300m 水,每小时排25 m ,全部排完只需300÷25=12(h),故自变量的取值范围是0≤t≤12.
(1)排水后的剩水量Q是排水时间t的函数,有Q=300-25t=-25t+300.
四、典型例题
(3)当t=5,代入上式,得Q=-5×25+300=175m ,即第5h末,游泳池内还有水175 m .
(4)当Q=150时,由150=-25t+300,得t=6(h),即第6h末池中有水150 m .
(3)开始排水后的第5h末,游泳池内还有多少水?
(4)当游泳池中还剩150 m 时,已经排水多少小时?
【当堂检测】
1.求下列中函数x=2的函数值,并指出自变量的范围:
(1)y=-3x+2; (2)y =2x2;
(3)
解:(1)当x=2时,y=-3x+2=-3×2+2=-4,自变量取值范围为R;
(2)当x=2时,y =2x2=2×22=8,自变量取值范围为R;
(3)当x=2时, ,自变量取值范围为x≠2.5
【当堂检测】
2.已知x与y的关系式为y=x+1,当y为2时,x值为( )
A. 1 B. 2 C. 3 D. -1
解:将y=2代入关系式y=x+1得2=x+1,解得x=1,故选A.
A
【当堂检测】
3.函数的三种表示方法分别是( )
A. 坐标法;画图法;解析式法
B. 画图法;列表法,解析式法
C. 图像法;列表法;解析式法
D. 图像法;列表法; 关系式法
函数有三种表示方法——图像法、列表法、解析式法,故选C.
C
【当堂检测】
4.从甲地到乙地的路程为300千米,一辆汽车从甲地到乙地,每小时行驶50千米,行驶的时间为t(小时),离乙地的路程为s(千米),则下表剩余两空应填( )
解:行驶的时间为t与离乙地的路程为s的关系式为s=300-50t,将t=5和t=6分别代入关系式可求得对应s的值为50和0,故选B.
t(小时) 1 2 3 4 5 6
s(千米) 250 200 150 100
B
A. 100;50 B. 50;0 C. 50;25 D. 250;300
【当堂检测】
5.某学校举办活动需购买一些气球,这些气球单价均为0.5元一个,假设购买数量为x,购买气球所要花费的总金额为y,则y与x的关系式为( )
解:总金额=单价×购买数量,故y与x的关系式为y=0.5x,故选A.
A. y=0.5x B. y=2x C. y=x+0.5 D. y=x-0.5
A
函数的表示方法
列表法、解析法和图象法
自变量的取值范围
使含自变量的等式有意义
使实际问题有意义
用列表法、解析法表示函数关系
五、课堂总结
