全等三角形的识别SSS
图片预览


文档简介
课件27张PPT。11.2全等三角形
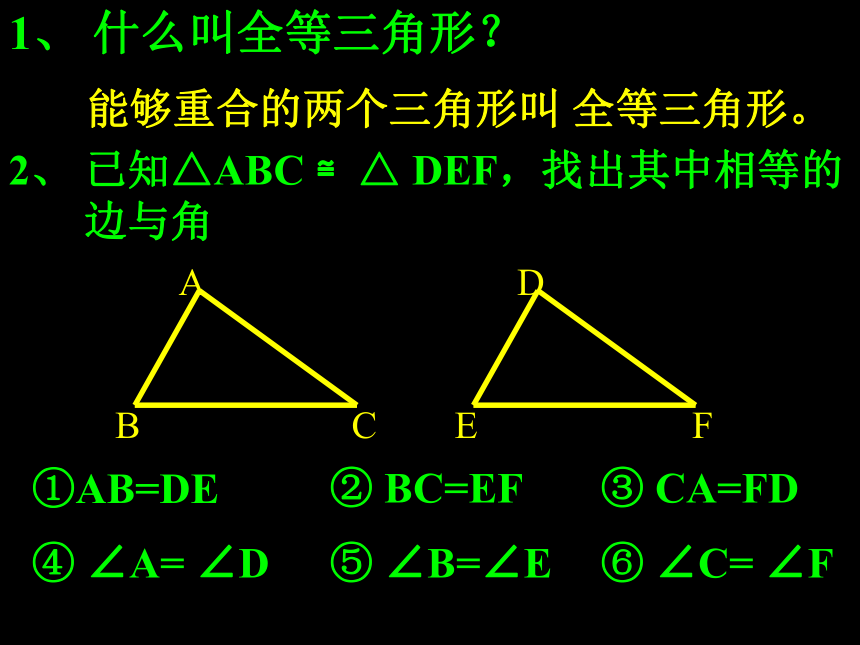
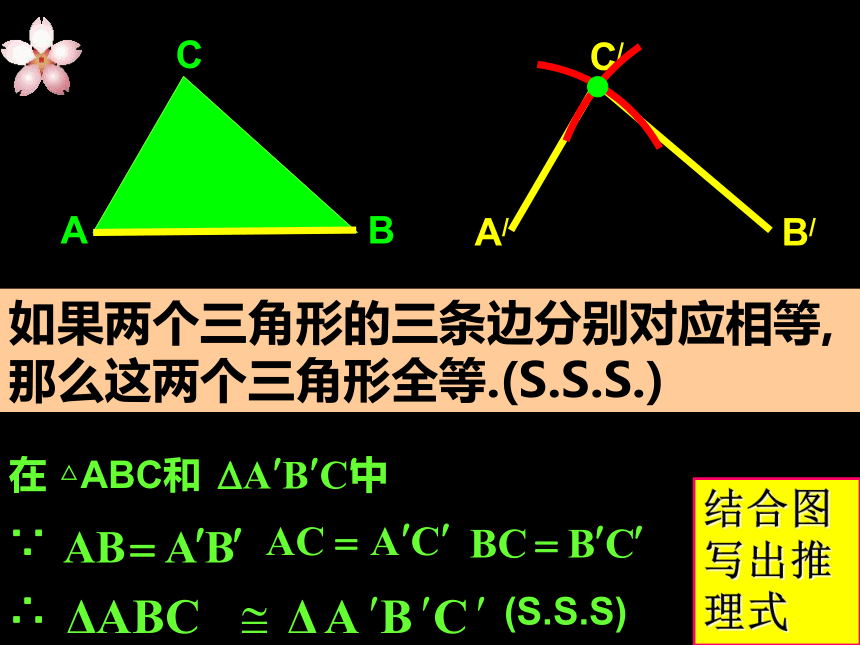
的判定1、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。2、 已知△ABC ≌△ DEF,找出其中相等的边与角①AB=DE③ CA=FD② BC=EF④ ∠A= ∠D⑤ ∠B=∠E⑥ ∠C= ∠F下面的两个三角形是全等三角形吗?如果两个三角形的三条边分别对应相等,那么这两个三角形全等吗?A/B/C/ABC在 △ABC和 中
∵
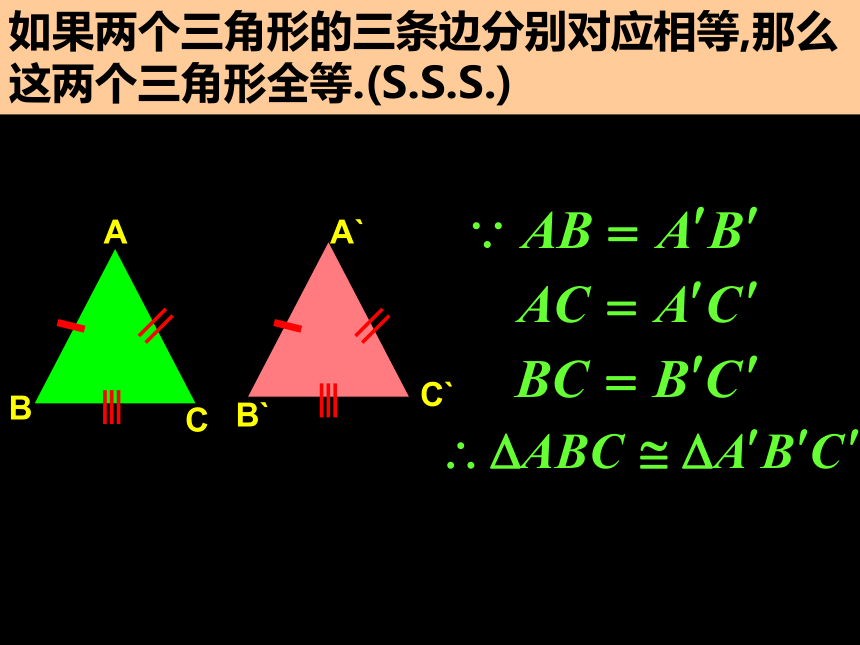
∴ (S.S.S) 结合图写出推理式如果两个三角形的三条边分别对应相等,
那么这两个三角形全等.(S.S.S.)11.2 全等三角形
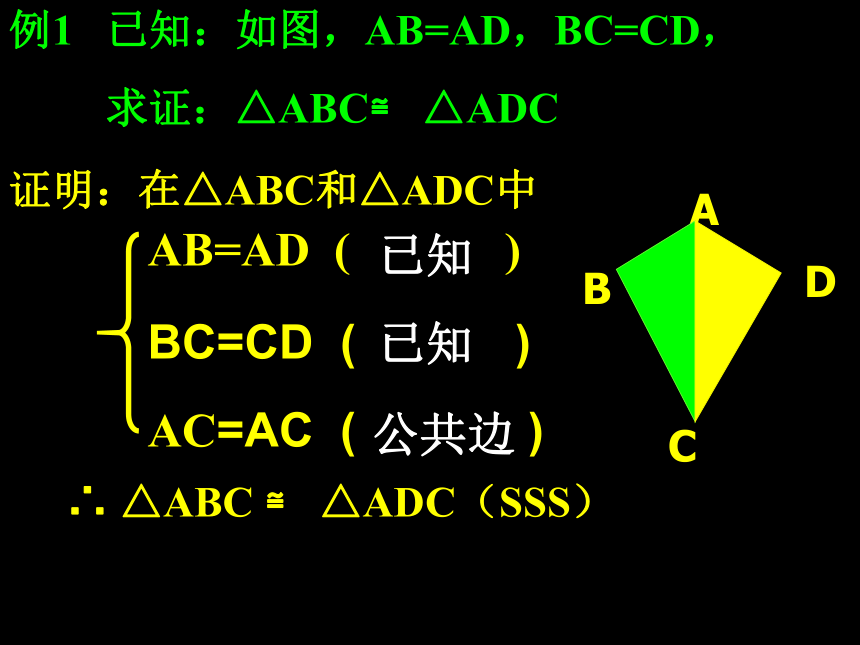
的判(SSS)(一)如果两个三角形的三条边分别对应相等,那么这两个三角形全等.(S.S.S.)BC=CD ( )例1 已知:如图,AB=AD,BC=CD,
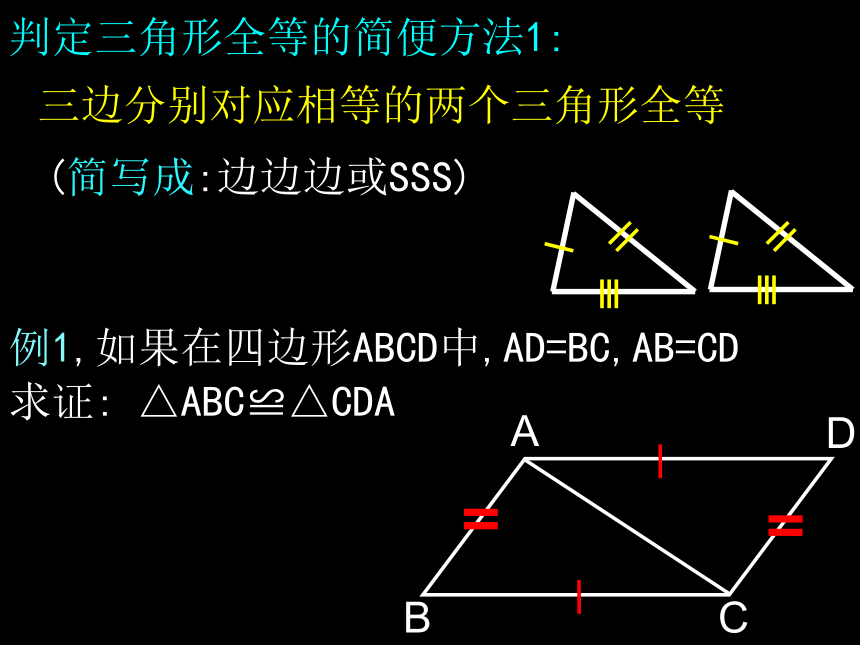
求证:△ABC≌ △ADCABCDAC=AC ( ) AB=AD ( )∴ △ABC ≌ △ADC(SSS)证明:在△ABC和△ADC中已知已知 公共边判定三角形全等的简便方法1:三边分别对应相等的两个三角形全等(简写成:边边边或SSS)例1,如果在四边形ABCD中,AD=BC,AB=CD
求证: △ABC≌△CDAABCD判定三角形全等的简便方法1:三边分别对应相等的两个三角形全等(简写成:边边边或SSS)练习1,如图,AC=AD,BC=BD
求证: △ABC≌△ABDABCD判定三角形全等的简便方法1:三边分别对应相等的两个三角形全等(简写成:边边边或SSS)练习2,如图,等腰△ABC中,AB=AC, AD是BC边上的中线.
求证: △ABD≌△ACDDABC作11.2 全等三角形
的判(SSS)(二)1、如图,AB=DC,AC=DB
求证: △ABC≌△DCBABCD(2)如图,D、F是线段BC上的两点,AB=CE,AF=DE, BD=FC, △ABF≌△ECDAEBFCD已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB ,AC=FE,BC=DE 证明△ABC ≌△ FDE,ACBDEF∠B=∠D如图,线段AC与BD相交于点, OA=OC,OB=OD,AB=CD,求证:△ABO≌ △CDOABCDOAB∥CD练习3:如图AD=BC,AB=CD
求证: ∠B=∠DDABC练习4,如图,AB=DC,AC=DB
求证: ∠A=∠DABCD A C B D证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例2 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证:△ABD≌△ACD根据条件识别下面的三角形是否全等?1、如图,AB=DC,AC=BD,则△ABC≌____理由_____, ∠DBC=400,则∠ACB=_____02、如图,AC=AD,BC=BD,则△ABC≌____理由______, ∠ACB=1200, ∠CAB=200则∠ABD=______020012003、如图,AB=CD,则添加条件______,就可以由SSS推得△ABC ≌ △CDA
4、点D、E、F、B在同一直线上,AB=CD, AE=EF,BF=DE则△ABE≌_______5、如图,AB=AC,点E是BC的中点,那么△ABE和△ACE全等吗?说明理由拓展思维,才能架起知识的桥梁……1.已知:如图,AB=AC,BD=CD.你能说明∠B=∠C吗?夯实基础, 才能有所突破 ……4.已知:如图,AB=DF,AC=DE,BE=CF.
试说明:四边形ABDF是平行四边形.2.如图,AD=BE,OD=OE,∠1=130o,∠2=25o.
根据上面的结论,你能得到哪些结论呢?
说出你的理由.拓展思维,才能架起知识的桥梁……3实践 , 探索中不断前进……康师傅有一块三角形的厚铁板(如图),
根据工作的需要,他想把∠MAN平分!
不过,他现在手头上只有一把没有刻度
的尺子和一根细绳,宋师傅感到很无奈…
你能只利用他手头的工具,给他想个法子吗?
并说明你的理由.回顾中,有所总结,有所收获……如果两个三角形的三条边分别对应相等,
那么这两个三角形全等.(S.S.S.)
的判定1、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。2、 已知△ABC ≌△ DEF,找出其中相等的边与角①AB=DE③ CA=FD② BC=EF④ ∠A= ∠D⑤ ∠B=∠E⑥ ∠C= ∠F下面的两个三角形是全等三角形吗?如果两个三角形的三条边分别对应相等,那么这两个三角形全等吗?A/B/C/ABC在 △ABC和 中
∵
∴ (S.S.S) 结合图写出推理式如果两个三角形的三条边分别对应相等,
那么这两个三角形全等.(S.S.S.)11.2 全等三角形
的判(SSS)(一)如果两个三角形的三条边分别对应相等,那么这两个三角形全等.(S.S.S.)BC=CD ( )例1 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADCABCDAC=AC ( ) AB=AD ( )∴ △ABC ≌ △ADC(SSS)证明:在△ABC和△ADC中已知已知 公共边判定三角形全等的简便方法1:三边分别对应相等的两个三角形全等(简写成:边边边或SSS)例1,如果在四边形ABCD中,AD=BC,AB=CD
求证: △ABC≌△CDAABCD判定三角形全等的简便方法1:三边分别对应相等的两个三角形全等(简写成:边边边或SSS)练习1,如图,AC=AD,BC=BD
求证: △ABC≌△ABDABCD判定三角形全等的简便方法1:三边分别对应相等的两个三角形全等(简写成:边边边或SSS)练习2,如图,等腰△ABC中,AB=AC, AD是BC边上的中线.
求证: △ABD≌△ACDDABC作11.2 全等三角形
的判(SSS)(二)1、如图,AB=DC,AC=DB
求证: △ABC≌△DCBABCD(2)如图,D、F是线段BC上的两点,AB=CE,AF=DE, BD=FC, △ABF≌△ECDAEBFCD已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB ,AC=FE,BC=DE 证明△ABC ≌△ FDE,ACBDEF∠B=∠D如图,线段AC与BD相交于点, OA=OC,OB=OD,AB=CD,求证:△ABO≌ △CDOABCDOAB∥CD练习3:如图AD=BC,AB=CD
求证: ∠B=∠DDABC练习4,如图,AB=DC,AC=DB
求证: ∠A=∠DABCD A C B D证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例2 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证:△ABD≌△ACD根据条件识别下面的三角形是否全等?1、如图,AB=DC,AC=BD,则△ABC≌____理由_____, ∠DBC=400,则∠ACB=_____02、如图,AC=AD,BC=BD,则△ABC≌____理由______, ∠ACB=1200, ∠CAB=200则∠ABD=______020012003、如图,AB=CD,则添加条件______,就可以由SSS推得△ABC ≌ △CDA
4、点D、E、F、B在同一直线上,AB=CD, AE=EF,BF=DE则△ABE≌_______5、如图,AB=AC,点E是BC的中点,那么△ABE和△ACE全等吗?说明理由拓展思维,才能架起知识的桥梁……1.已知:如图,AB=AC,BD=CD.你能说明∠B=∠C吗?夯实基础, 才能有所突破 ……4.已知:如图,AB=DF,AC=DE,BE=CF.
试说明:四边形ABDF是平行四边形.2.如图,AD=BE,OD=OE,∠1=130o,∠2=25o.
根据上面的结论,你能得到哪些结论呢?
说出你的理由.拓展思维,才能架起知识的桥梁……3实践 , 探索中不断前进……康师傅有一块三角形的厚铁板(如图),
根据工作的需要,他想把∠MAN平分!
不过,他现在手头上只有一把没有刻度
的尺子和一根细绳,宋师傅感到很无奈…
你能只利用他手头的工具,给他想个法子吗?
并说明你的理由.回顾中,有所总结,有所收获……如果两个三角形的三条边分别对应相等,
那么这两个三角形全等.(S.S.S.)
