全等三角形的识别ASA、AAS
文档属性
| 名称 | 全等三角形的识别ASA、AAS |  | |
| 格式 | rar | ||
| 文件大小 | 42.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-22 20:12:00 | ||
图片预览

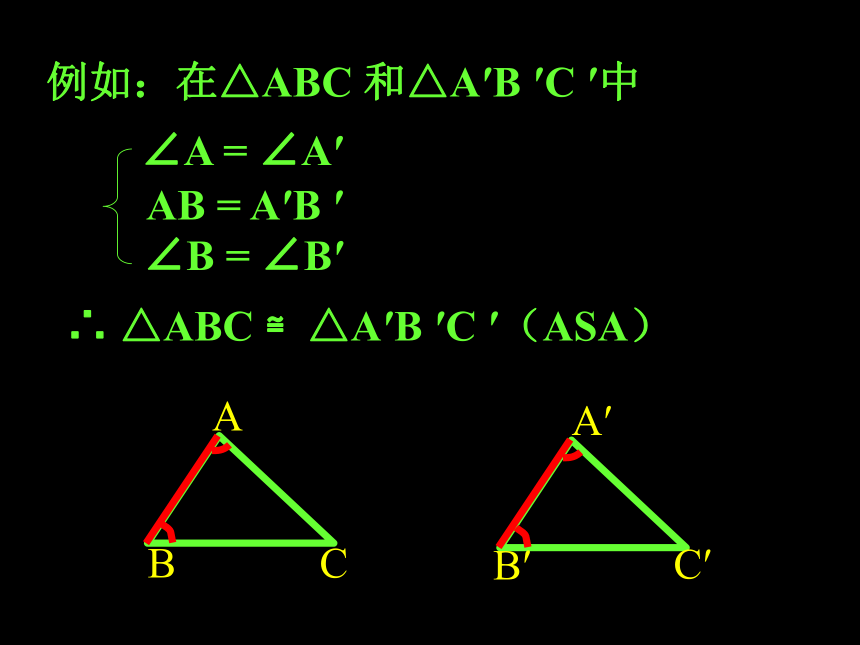
文档简介
课件15张PPT。全等三角形识别
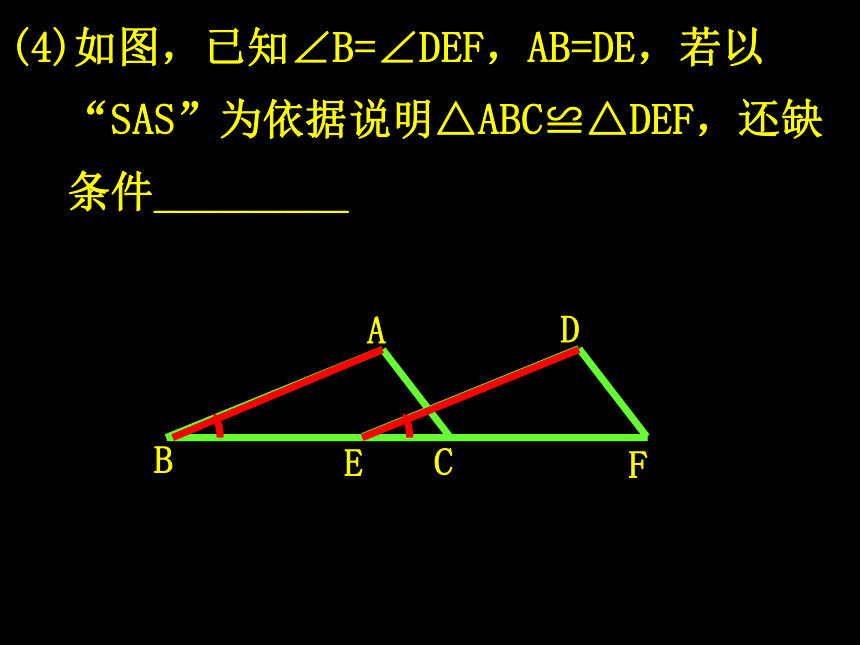
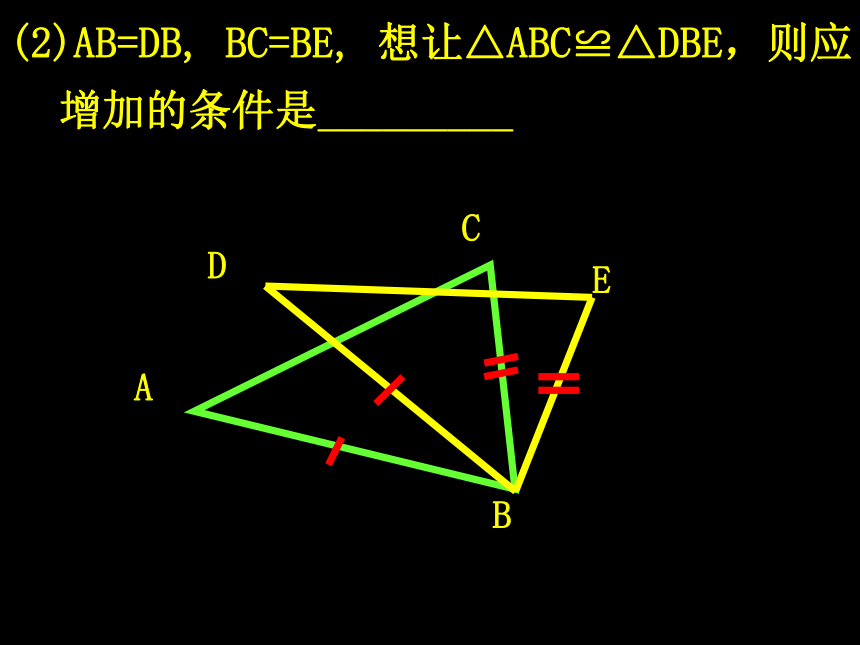
ASA、AAS(4)如图,已知∠B=∠DEF,AB=DE,若以“SAS”为依据说明△ABC≌△DEF,还缺条件_________(2)AB=DB, BC=BE, 想让△ABC≌△DBE,则应增加的条件是_________1.任意画一个△ABC2.画线段B′C′= BC3.在B′C′的同旁分别以B′C′为顶点画 ∠MB′C′=∠B,∠NC′B′=∠C, MB′与NC′交于A′.B′C′MNA′角边角公理
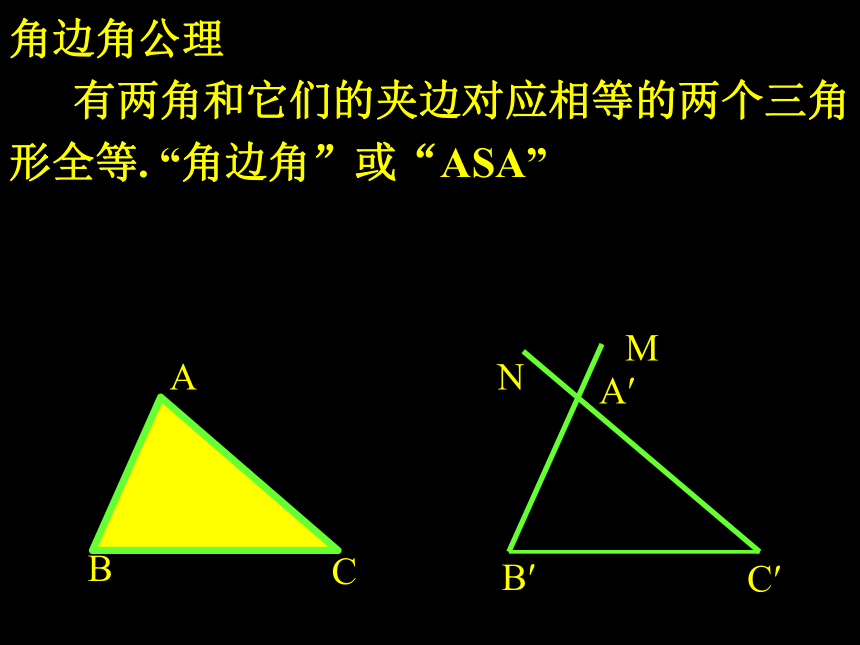
有两角和它们的夹边对应相等的两个三角形全等. “角边角”或“ASA”
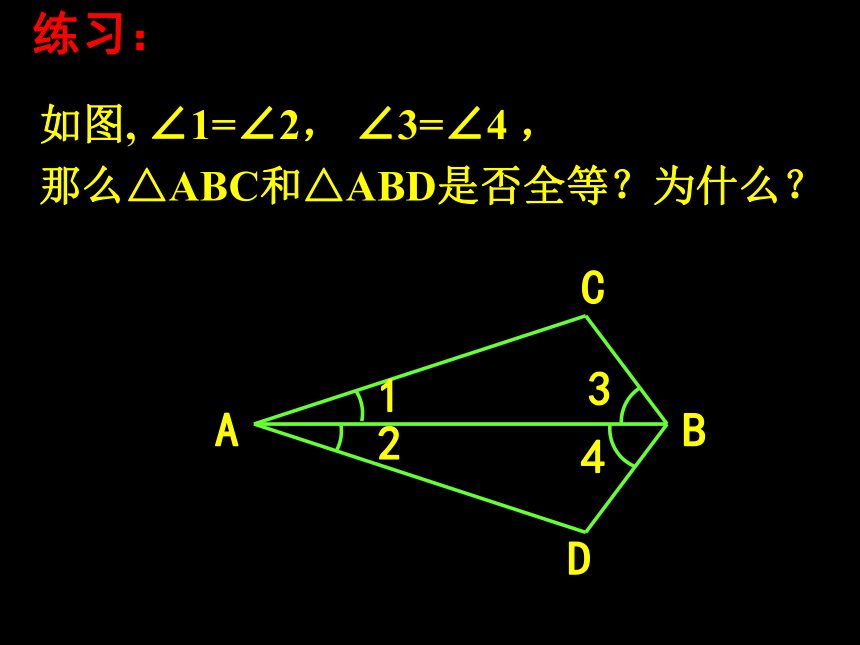
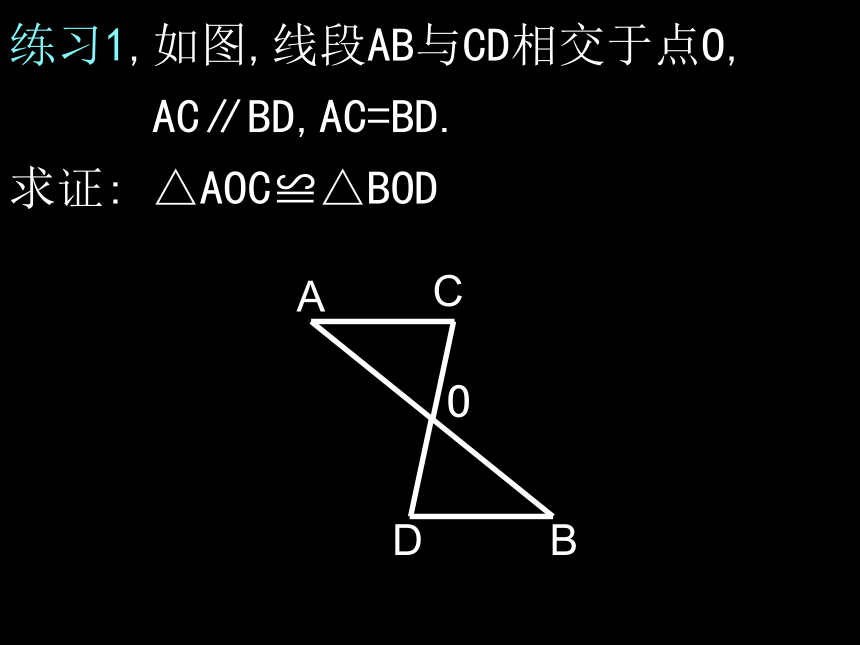
例如:在△ABC 和△A′B ′C ′中AB = A′B ′∠B = ∠B′∴ △ABC ≌△A′B ′C ′(ASA)∠A = ∠A′练习:如图, ∠1=∠2, ∠3=∠4 , 那么△ABC和△ABD是否全等?为什么?ACDB3412练习1,如图,线段AB与CD相交于点O, AC∥BD,AC=BD.
求证: △AOC≌△BODDBCAO例:如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB = AC,∠B = ∠C △ABE≌△ACD成立吗?练习:如图,∠CAB=∠DBA,∠1=∠2, 试说明△ABC≌△ABD.ACDB12练习2
如图,AD=BC,∠1=∠2.
求证: △AOD≌△BOCABCD12O(简写成:角边角或ASA)判定三角形全等的简便方法3:两角和它们的夹边分别对应相等的两个三角形全等练习3
如图,AB=AC,∠B=∠C.
求证: BE=CDDCABE练习4,如图,∠1=∠2, ∠B=∠D,AB=AD.
求证: △ABC≌△ADEABCD1E2角边角公理 有两角和它们的夹边对应相等的两个三角形全等. 简记为“角边角”或“ASA”在△ABC 和△A′B ′C ′中AB = A′B ′∠C = ∠C′△ABC ≌△A′B ′C ′∠A = ∠A′角角边公理 有两角和一边对应相等的两个三角形全等. 简记为“角角边”或“AAS”已知:如图,∠1 = ∠2,∠C = ∠D
求证:AC = ADBACD8、如图,∠C=∠D,∠1=∠2 ,AD=EC.
试说明BD=BC12E3
ASA、AAS(4)如图,已知∠B=∠DEF,AB=DE,若以“SAS”为依据说明△ABC≌△DEF,还缺条件_________(2)AB=DB, BC=BE, 想让△ABC≌△DBE,则应增加的条件是_________1.任意画一个△ABC2.画线段B′C′= BC3.在B′C′的同旁分别以B′C′为顶点画 ∠MB′C′=∠B,∠NC′B′=∠C, MB′与NC′交于A′.B′C′MNA′角边角公理
有两角和它们的夹边对应相等的两个三角形全等. “角边角”或“ASA”
例如:在△ABC 和△A′B ′C ′中AB = A′B ′∠B = ∠B′∴ △ABC ≌△A′B ′C ′(ASA)∠A = ∠A′练习:如图, ∠1=∠2, ∠3=∠4 , 那么△ABC和△ABD是否全等?为什么?ACDB3412练习1,如图,线段AB与CD相交于点O, AC∥BD,AC=BD.
求证: △AOC≌△BODDBCAO例:如图,点D在AB上,点E在AC上,BE和CD相交于点O,AB = AC,∠B = ∠C △ABE≌△ACD成立吗?练习:如图,∠CAB=∠DBA,∠1=∠2, 试说明△ABC≌△ABD.ACDB12练习2
如图,AD=BC,∠1=∠2.
求证: △AOD≌△BOCABCD12O(简写成:角边角或ASA)判定三角形全等的简便方法3:两角和它们的夹边分别对应相等的两个三角形全等练习3
如图,AB=AC,∠B=∠C.
求证: BE=CDDCABE练习4,如图,∠1=∠2, ∠B=∠D,AB=AD.
求证: △ABC≌△ADEABCD1E2角边角公理 有两角和它们的夹边对应相等的两个三角形全等. 简记为“角边角”或“ASA”在△ABC 和△A′B ′C ′中AB = A′B ′∠C = ∠C′△ABC ≌△A′B ′C ′∠A = ∠A′角角边公理 有两角和一边对应相等的两个三角形全等. 简记为“角角边”或“AAS”已知:如图,∠1 = ∠2,∠C = ∠D
求证:AC = ADBACD8、如图,∠C=∠D,∠1=∠2 ,AD=EC.
试说明BD=BC12E3
