人教版七年级数学上册 第二章整式的加减 解答题培优提升专题训练(含答案)
文档属性
| 名称 | 人教版七年级数学上册 第二章整式的加减 解答题培优提升专题训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 191.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 00:00:00 | ||
图片预览




文档简介
人教版七年级数学上册《整式的加减》解答题培优提升专题训练(附答案)
1.圆圆同学在做一道改编自课本上的习题时,解答过程如下:
(1)已知圆圆的解答是错误的,则他开始出现错误是在第 步;
(2)请给出正确的计算过程.
2.先化简,再求值:
(1)4xy2+6xy﹣2(4xy﹣2)﹣[﹣2(xy2+xy)],其中x3=﹣,|y+1|=2;
(2)已知x2+3x+4=1,求﹣4x2﹣y2﹣2(﹣x2+3x﹣y2)的值.
3.若关于a,b的多项式2(a3﹣3ab+3)+(a3+kab)化简后不含有ab的项,求字母k的值.
4.已知多项式A=x2+xy+3y,B=x2﹣xy.
(1)已知(x﹣3)2022+|y+5|=0,求3A﹣2B的值;
(2)若3A﹣2B的值与y的取值无关,求x的值.
5.小红做一道数学题“两个整式A,B,已知B为4x2﹣5x﹣6,试求A+2B的值“.小红误将A+2B看成A﹣2B,结果答案(计算正确)为﹣7x2+10x+12.
(1)求整式A;
(2)求出当x=﹣3时,A+2B的值.
6.已知多项式M、N,其中N=2m2﹣3m﹣2,在计算M+N时,某同学误将其看成了M﹣N,求得结果为3m2﹣2m﹣5.
(1)求多项式M;
(2)请帮助该同学计算出正确的结果.
7.已知多项式A=2b2﹣ab,B=b2+4ab﹣5,C=﹣2b2﹣mab+3.
(1)若ab=﹣1,求A﹣2B的值.
(2)若2B﹣3C中不含ab的项,求有理数m的值.
8.已知有下列两个代数式:①a2﹣b2;②(a+b)(a﹣b).
(1)当a=7,b=3时,代数式①的值是 ;代数式②的值是 .
(2)当a=﹣2,b=﹣5时,代数式①的值是 ;代数式②的值是 .
(3)观察(1)和(2)中代数式的值,你发现代数式a2﹣b2和(a+b)(a﹣b)的关系为 .
(4)利用你发现的规律,求20222﹣20212的值.
9.一种钢笔在A、B两家文具店的零售价均为10元/支.A店的优惠办法是一次性购买4支以上,超过4支的部分按零售价的6折出售.
(1)小明在A店一次性购买这种钢笔3支需付款 元,一次性购买5支需付款 元;
(2)设小明在A店一次性购买这种钢笔x支(x>4),需要付款多少元?(用含x的代数式表示)
(3)B店的优惠办法是不论购买多少支钢笔,一律按零售价的8折出售.请通过计算说明,若小明一次性购买10支这种钢笔,他在哪个店购买更划算?
10.某商店从批发市场以每个a元的成本价购进50个A品牌的排球,然后每个加价b元后出售.
(1)全部售出50个排球的总利润为 元.
(2)若商店在成功售出30个排球后,决定将剩余20个排球按售价8折出售,全部售完后实际盈利比按原价售卖的盈利少多少元?请列式计算.
(3)若商店同时出售A、B两种品牌的排球,B每个售价比A多10元,小红准备买三个排球,恰好商店举行优惠活动“买三免一”,即任意买三个排球(不限品牌)则价格最低的一个排球免费,小红有哪几种购买方式?付款金额分别是多少?
11.小韩和同学们在一家快餐店吃饭,如表为快餐店的菜单:
种类 配餐 价格(元) 优惠活动
A餐 1份盖饭 20 消费满150元,减24元 消费满300元,减48元 ……
B餐 1份盖饭+1杯饮料 28
C餐 1份盖饭+1杯饮料+1份小菜 32
小韩记录大家的点餐种类,并根据菜单一次点好,已知他们所点的餐共有11份盖饭,x杯饮料和5份小菜.
(1)他们共点了 份B餐;
(2)若他们至少需要7杯饮料,要使所花费的钱数最少,则应该点几份B餐.
12.某服装厂生产一种夹克和T恤,夹克每件定价100元,T恤每件定价50元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款.现某客户要到该服装厂购买夹克30件,T恤x件(x>30).
(1)若该客户按方案①购买,需付款 元(用含x的式子表示);若该客户按方案②购买,需付款 元(用含x的式子表示);
(2)若x=40,通过计算说明按方案①、方案②哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当x=40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
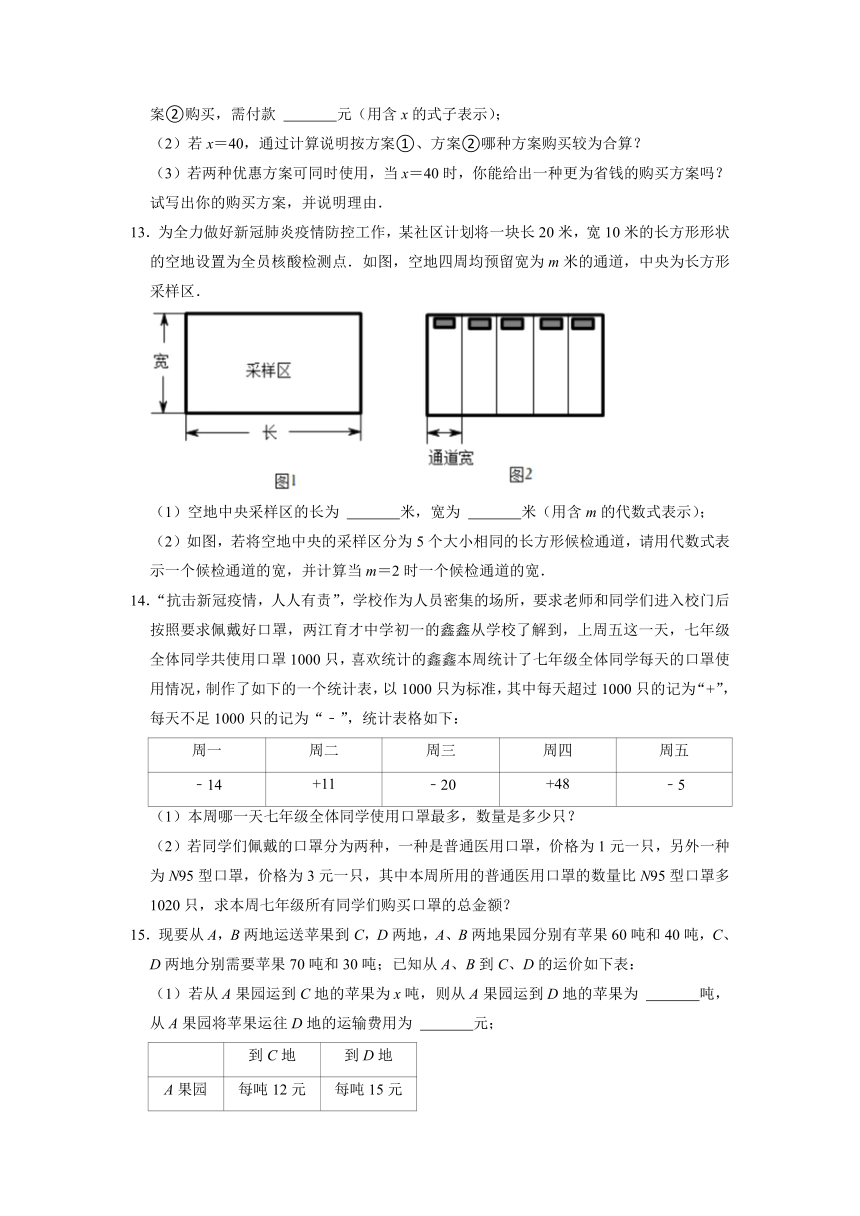
13.为全力做好新冠肺炎疫情防控工作,某社区计划将一块长20米,宽10米的长方形形状的空地设置为全员核酸检测点.如图,空地四周均预留宽为m米的通道,中央为长方形采样区.
(1)空地中央采样区的长为 米,宽为 米(用含m的代数式表示);
(2)如图,若将空地中央的采样区分为5个大小相同的长方形候检通道,请用代数式表示一个候检通道的宽,并计算当m=2时一个候检通道的宽.
14.“抗击新冠疫情,人人有责”,学校作为人员密集的场所,要求老师和同学们进入校门后按照要求佩戴好口罩,两江育才中学初一的鑫鑫从学校了解到,上周五这一天,七年级全体同学共使用口罩1000只,喜欢统计的鑫鑫本周统计了七年级全体同学每天的口罩使用情况,制作了如下的一个统计表,以1000只为标准,其中每天超过1000只的记为“+”,每天不足1000只的记为“﹣”,统计表格如下:
周一 周二 周三 周四 周五
﹣14 +11 ﹣20 +48 ﹣5
(1)本周哪一天七年级全体同学使用口罩最多,数量是多少只?
(2)若同学们佩戴的口罩分为两种,一种是普通医用口罩,价格为1元一只,另外一种为N95型口罩,价格为3元一只,其中本周所用的普通医用口罩的数量比N95型口罩多1020只,求本周七年级所有同学们购买口罩的总金额?
15.现要从A,B两地运送苹果到C,D两地,A、B两地果园分别有苹果60吨和40吨,C、D两地分别需要苹果70吨和30吨;已知从A、B到C、D的运价如下表:
(1)若从A果园运到C地的苹果为x吨,则从A果园运到D地的苹果为 吨,从A果园将苹果运往D地的运输费用为 元;
到C地 到D地
A果园 每吨12元 每吨15元
B果园 每吨8元 每吨10元
(2)用含x的式子表示出总运输费.
16.小明为一个长方形的生活娱乐场所提供了如下的设计方案,其中扇形的水池区和三角形的儿童娱乐区外的地方都是绿地,并且AB=a,AD=b,AF=AB.
(1)用含a,b的式子表示绿地的面积;
(2)若长宽之间满足a=2b,这个生活娱乐场所需要绿地面积占总面积的以上,那么小明的设计方案符合要求吗?试说明理由.
17.某市居民使用自来水按如下标准收费:若每户月用水不超过12m3,按a元/m3收费;若超过12m3,但不超过20m3,则超过部分按1.5a元m3收费;若超过20m3,超过部分按2a元/m3收费.
户月用水量/m3 10 16 n(n>20)
收费金额/元 10a
(1)若某月用水量为16m3,收费金额为 元(用含a的式子表示);
(2)列式表示月用水量为n(n>20)m3时的收费金额.
18.为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如表(注:水费按一个月结算一次):请根据价目表的内容解答下列问题:
每月用水量(m3) 单价(元/m3)
不超出26m3的部分 3
超出26m3不超出34m3的部分 4
超出34m3的部分 7
(1)填空:若该户居民1月份用水20立方米,则应收水费 元;若该户2月份用水30立方米,则应收水费 元;
(2)若该户居民3月份用水x立方米(其中26<x≤34),则应收水费多少元?(结果用含x的代数式表示)
(3)若该户居民3月份用水a立方米(其中a>34),则应收水费多少元?(结果用含a的代数式表示)
19.为丰富第二课堂活动,学校增设了羽毛球社团.计划为羽毛球社团每位成员购买某品牌羽毛球拍1支、羽毛球3筒,并购羽毛球40筒作为社团备用球.经了解,该品牌羽毛球拍定价为100元/支,羽毛球20元/筒.现有甲、乙两家体育用品商店经销该品牌产品,均有优惠促销.甲商店促销方法是买一支羽毛球拍送一筒羽毛球;乙商店则是所有商品都按90%付款.设参加羽毛球社团的同学为x名,根据题意完成下列问题.
(1)购买方案一:全部到甲商店购买,需要支付 元,
购买方案二:全部到乙商店购买,需要支付 元;
(2)当x=15,请通过计算说明采用(1)中的哪个方案较为优惠;
(3)当x=30,聪明的你能否根据甲、乙两商店的促销信息,找到一种比(1)中两个方案更优惠的购买方法,请写出方案并列式求出所需费用,同时直接写出分别比采用(1)中两种方案各省多少钱.
20.为报名参加泉州台商投资区运动会首届羽毛球比赛项目,某校羽毛球队需要购买6支羽毛球拍和x盒羽毛球(x>6),羽毛球拍市场价为150元/支,羽毛球为30元/盒,以下是泉州台商投资区本地的两家商场提供竞标方案:
甲商场竞标方案为:所有商品九折.
乙商场竞标方案为:买1支羽毛球拍送1盒羽毛球,其余原价销售.请你根据两家商场提供的竞标方案完成下列问题:
(1)分别用含x的代数式表示在甲商场和乙商场购买所有物品的费用.
(2)当x=20时,请通过计算说明选择哪个商场购买比较省钱.
(3)当x=20时,请根据两家商场所提供的竞标方案,拟出一种折中的新方案,通过计算说明你设计的新方案所需的费用最少,并求出新方案的费用.
21.如图1.在数轴上点M表示的数为m,点N表示的数为n,点M到点N的距离记为MN.
如图2:在数轴上点A表示数a,点B表示数b,点C表示数c,a是3的相反数,b是最大的负整数,c是多项式2x3y2﹣3x+1的次数.
(1)a= ,b= ,c= ;
(2)若将数轴折叠,使得A点与C点重合,求与点B重合的点表示的数;
(3)点A、B、C开始在数轴上运动,若点B以每秒1个单位长度的速度向左运动,同时,点A和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,运动时间为t秒;
探究:3BC﹣4AB的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求其值.
参考答案
1.解:(1)他开始出现错误是在第①步,
故答案为:①;
(2)原式=5a2﹣2a﹣1﹣12+8a﹣4a2
=a2+6a﹣13.
2.解:(1)原式=4xy2+6xy﹣8xy+4﹣(﹣2xy2﹣2xy)
=4xy2﹣2xy+4+2xy2+2xy
=6xy2+4,
由题意可知:x=﹣,y+1=±2,
∴x=﹣,y=1或﹣3,
当x=﹣,y=1时,
原式=6×(﹣)×1+4
=﹣3+4
=1,
当x=﹣,y=﹣3时,
原式=6×(﹣)×9+4
=﹣27+4
=﹣23.
(2)原式=﹣4x2﹣y2+2x2﹣6x+y2
=﹣2x2﹣6x,
∵x2+3x+4=1,
∴x2+3x=﹣3,
∴原式=﹣2(x2+3x)
=﹣2×(﹣3)
=6.
3.解:原式=2a3﹣6ab+6+a3+kab
=3a3+(k﹣6)ab+6,
由题意可知:k﹣6=0,
∴k=6.
4.解:(1)3A﹣2B
=3(x2+xy+3y)﹣2(x2﹣xy)
=3x2+3xy+9y﹣2x2+2xy
=x2+5xy+9y,
由题意可知:x﹣3=0,y+5=0,
∴x=3,y=﹣5,
∴原式=9+5×3×(﹣5)+9×(﹣5)
=9﹣75﹣45
=﹣111.
(2)3A﹣2B=x2+5xy+9y
=x2+(5x+9)y,
令5x+9=0,
∴x=﹣.
5.解:(1)∵A﹣2B=﹣7x2+10x+12,B=4x2﹣5x﹣6,
∴A=(﹣7x2+10x+12)+2B
=﹣7x2+10x+12+2(4x2﹣5x﹣6)
=﹣7x2+10x+12+8x2﹣10x﹣12
=x2;
(2)A+2B
=x2+2(4x2﹣5x﹣6)
=x2+8x2﹣10x﹣12
=9x2﹣10x﹣12;
当x=﹣3时,
A+2B
=9×(﹣3)2﹣10×(﹣3)﹣12
=9×9+30﹣12
=81+30﹣12
=99.
6.解:(1)由题意可得:M﹣N=3m2﹣2m﹣5,
则M﹣(2m2﹣3m﹣2)=3m2﹣2m﹣5,
故M=3m2﹣2m﹣5+2m2﹣3m﹣2
=5m2﹣5m﹣7;
(2)由(1)得:M+N=5m2﹣5m﹣7+2m2﹣3m﹣2
=7m2﹣8m﹣9.
7.解:(1)原式=(2b2﹣ab)﹣2(b2+4ab﹣5)
=2b2﹣ab﹣2b2﹣8ab+10
=﹣9ab+10,
当ab=﹣1时,
原式=﹣9×(﹣1)+10=9+10=19;
(2)2B﹣3C
=2(b2+4ab﹣5)﹣3(﹣2b2﹣mab+3)
=2b2+8ab﹣10+6b2+3mab﹣9
=8b2+(8+3m)ab﹣19,
∵2B﹣3C的值不含ab的项,
∴8+3m=0,
解得m=,
即m的值为:.
8.解:(1)当a=7,b=3时,a2﹣b2=49﹣9=40,
(a+b)(a﹣b)=10×4=40,
故答案为:40,40;
(2)当a=﹣2,b=﹣5时,a2﹣b2=4﹣25=﹣21,
(a+b)(a﹣b)=(﹣7)×3=﹣21,
故答案为:﹣21,﹣21;
(3)通过(1)(2)中代数式的值,可知a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(4)根据(3)中的规律,可得20222﹣20212=(2022+2021)×(2022﹣2021)=4043.
9.解:(1)在A店一次性购买这种钢笔3支需付款3×10=30(元),一次性购买5支需付款4×10+(5﹣4)×10×0.6=46(元),
故答案为:30,46;
(2)∵4×10+(x﹣4)×10×0.6=6x+16,
∴在A店一次性购买这种钢笔x支(x>4),需要付款(6x+16)元;
(3)一次性购买10支这种钢笔,在A店需要付款6x+16=6×10+16=76(元),
在B店需要付款10×10×0.8=80(元),
∵76<80,
∴他在A店购买更划算.
10.解:(1)根据题意得:全部售出50个排球的总利润为50b元.
故答案为:50b;
(2)根据题意得:50b﹣30b﹣20[0.8(a+b)﹣a]
=50b﹣30b﹣20[0.8a+0.8b﹣a]
=50b﹣30b﹣20[0.8b﹣0.2a]
=50b﹣30b﹣16b+4a
=(4a+4b)元.
答:全部售完后实际盈利比按原价售卖的盈利少(4a+4b)元;
(3)设小红购买x个A品牌的排球,则购买(3﹣x)个B品牌的排球,
∵x,(3﹣x)均为自然数,
∴x可以为0,1,2,3,
∴小红共有4种购买方案,
方案1:购买3个A品牌的排球,付款金额为2(a+b)元;
方案2:购买2个A品牌的排球,1个B品牌的排球,付款金额为(a+b)+(a+b+10)=(2a+2b+10)元;
方案3:购买1个A品牌的排球,2个B品牌的排球,付款金额为2(a+b+10)元;
方案4:购买3个B品牌的排球,付款金额为2(a+b+10)元.
11.解:(1)由题意得:B餐的份数为:x﹣5,
故答案为:(x﹣5);
(2)A餐的份数为:11﹣x,
B餐的份数为:x﹣5,
则所花费的钱数为:20(11﹣x)+28(x﹣5)+32×5
=220﹣20x+28x﹣140+160
=6x+240,
∵至少需要7杯饮料,
∴当x=7时,所花费的钱数是:6×7+240=282(元),
则所点的B餐的份数为:7﹣5=2(份).
答:应该点2份B餐.
12.解:(1)按方案①购买,需付款100×30+50(x﹣30)=(50x+1500)元,
按方案②购买,需付款100×0.8×30+50×0.8x=(40x+2400)元,
故答案为:(50x+1500),(40x+2400);
(2)若x=40时,选择方案①购买较为合算,理由如下:
方案①共需付款:1500+50x=1500+50×40=3500(元),
方案②共需付款:2400+40x=2400+40×40=4000(元).
故选择方案①购买较为合算;
(3)按方案①购买夹克30件,再按方案②购买T恤10件更为省钱,理由如下:
方案①共需付款:1500+50x=1500+50×40=3500(元),
方案②共需付款:2400+40x=2400+40×40=4000(元).
按方案①购买夹克30件,再按方案②购买T恤10件共需付款:1500+50×30+10×50×80%=3400(元),
∵3400<3500<4000,
∴按方案①购买夹克30件,再按方案②购买T恤10件更为省钱.
13.解:(1)原长方形的长为20米,宽为10米,在四周均预留宽为m米的通道后,
中央核酸检测区的长为(20﹣2m)米,宽为(10﹣2m)米,
故答案为:(20﹣2m),(10﹣2m);
(2)将中央核酸检测区的“长”平均分成5份为,;
当m=2时,==3.2(米),
答:一个候检通道的宽为米,当m=2时一个候检通道的宽为3.2米.
14.解:(1)由题意得﹣20<﹣14<﹣5<+11<+48,
48+1000=1048(只),
答:本周周四这天七年级同学使用口罩最多,数量是1048只;
(2)本周共使用口罩数量为:1000×5+(﹣14+11﹣20+48﹣5)
=5000+20
=5020(只),
设本周使用N95型口罩x只,
得x+x+1020=5020,
解得x=2000,
∴x+1020=2000+1020=3020(只),
∴1×3020+3×2000
=3020+6000
=9020(元),
答:本周七年级所有同学们购买口罩的总金额为9020元.
15.解:(1)∵从A果园运到C地的苹果为x吨,
∴从A果园运到D地的苹果为(60﹣x)吨,从B果园运到C地的苹果为(70﹣x)吨,运到D地的苹果为15(60﹣x)=(900﹣15x)吨,
故答案为:(60﹣x),(900﹣15x);
(2)总运输费为12x+15(60﹣x)+8(70﹣x)+10(x﹣30)
=12x+900﹣15x+560﹣8x+10x﹣300
=﹣x+1160(元).
16.解:(1)绿地的面积为:ab﹣a ﹣πb2=ab﹣πb2;
(2)当a=2b时,
绿地面积为:ab﹣πb2=(﹣π)b2,
(﹣π)b2÷2b2=<,
所以小明的设计方案不符合要求.
17.解:(1)当用水量为16m3时.
12a+1.5a(16﹣12)=12a+6a=18a.
答:月用水量为16m3时,收费金额为18a元.
(2)当用水量为nm3时.
12a+1.5a(20﹣12)+2a(n﹣20)
=12a+12a+2na﹣40a
=(2na﹣16a)m3
答:月用水量为n(n>20)m3时的收费(2na﹣16a)m3.
18.解:(1)3×20=60(元),
3×26+4×(30﹣26)
=3×26+4×4
=78+16
=94(元).
故答案为:60;94.
(2)依题意得:应收水费为3×26+4×(x﹣26)=(4x﹣26)元.
故应收水费(4x﹣26)元;
(3)依题意得:应收水费为3×26+4×(34﹣26)+7(a﹣34)=(7a﹣128)元.
故应收水费(7a﹣128)元.
19.解:(1)甲商店购买需付款:100x+(3x﹣x+40)×20=140x+800(元),
乙商店购买需付款90%×100x+20×90%(3x+40)=144x+720(元),
故答案为:(140x+800),(144x+720);
(2)当x=15时,
甲商店需:140×15+800=2900(元),
乙商店需:144×15+720=2880(元),
因为2900>2880,
所以乙商店购买合算;
(3)先在甲商店购买30支球拍,送30筒球需3000元,剩下100筒球在乙商店购买需1800元,共需4800元,
甲商店购买需:140×30+800=5000(元),
乙商店购买需:144×30+720=5040(元),
5000﹣4800=200(元),5040﹣4800=240(元),
比甲商店省200元,比乙商店省240元.
20.解:(1)在甲商场购买所有物品的费用为:0.9(6×150+30x)=(27x+810)(元),
在乙商场购买所有物品的费用为:6×150+30(x﹣6)=(30x+720)(元);
(2)当x=20时,27x+810=1350(元);
30x+720=1320(元);
1350>1320,
答:选择乙商场购买比较省钱.
(3)当x=20时,
在乙商场购买6支羽毛球拍和6盒羽毛球的费用为:
6×150=900(元);
在甲商场购买14盒羽毛球的费用为:
30×14×0.9=378(元);
合计的费用为:900+378=1278(元).
所以在甲商场购买14盒羽毛球、在乙商场购买6支羽毛球拍和6盒羽毛球费用最少,只要1278元.
21.解:(1)∵a是3的相反数,b是最大的负整数,c是多项式2x3y2﹣3x+1的次数,
∴a=﹣3,b=﹣1,c=5,
故答案为:﹣3,﹣1,5;
(2)当﹣3与5重合时,折叠点是1,
∴1﹣(﹣1)=2,1+2=3,
故与点B重合的点表示的数是3;
(3)A:﹣3+2t,B:﹣1﹣t,C:5+3t,
∴BC=(5+3t)﹣(﹣1﹣t)=6+4t,
AB=(﹣1﹣t)﹣(﹣3+2t)=2﹣3t,
∴3BC﹣4AB=3(6+4t)﹣4(2﹣3t)=10;
答:3BC﹣4AB=10是定值,不随着时间的变化而改变.
1.圆圆同学在做一道改编自课本上的习题时,解答过程如下:
(1)已知圆圆的解答是错误的,则他开始出现错误是在第 步;
(2)请给出正确的计算过程.
2.先化简,再求值:
(1)4xy2+6xy﹣2(4xy﹣2)﹣[﹣2(xy2+xy)],其中x3=﹣,|y+1|=2;
(2)已知x2+3x+4=1,求﹣4x2﹣y2﹣2(﹣x2+3x﹣y2)的值.
3.若关于a,b的多项式2(a3﹣3ab+3)+(a3+kab)化简后不含有ab的项,求字母k的值.
4.已知多项式A=x2+xy+3y,B=x2﹣xy.
(1)已知(x﹣3)2022+|y+5|=0,求3A﹣2B的值;
(2)若3A﹣2B的值与y的取值无关,求x的值.
5.小红做一道数学题“两个整式A,B,已知B为4x2﹣5x﹣6,试求A+2B的值“.小红误将A+2B看成A﹣2B,结果答案(计算正确)为﹣7x2+10x+12.
(1)求整式A;
(2)求出当x=﹣3时,A+2B的值.
6.已知多项式M、N,其中N=2m2﹣3m﹣2,在计算M+N时,某同学误将其看成了M﹣N,求得结果为3m2﹣2m﹣5.
(1)求多项式M;
(2)请帮助该同学计算出正确的结果.
7.已知多项式A=2b2﹣ab,B=b2+4ab﹣5,C=﹣2b2﹣mab+3.
(1)若ab=﹣1,求A﹣2B的值.
(2)若2B﹣3C中不含ab的项,求有理数m的值.
8.已知有下列两个代数式:①a2﹣b2;②(a+b)(a﹣b).
(1)当a=7,b=3时,代数式①的值是 ;代数式②的值是 .
(2)当a=﹣2,b=﹣5时,代数式①的值是 ;代数式②的值是 .
(3)观察(1)和(2)中代数式的值,你发现代数式a2﹣b2和(a+b)(a﹣b)的关系为 .
(4)利用你发现的规律,求20222﹣20212的值.
9.一种钢笔在A、B两家文具店的零售价均为10元/支.A店的优惠办法是一次性购买4支以上,超过4支的部分按零售价的6折出售.
(1)小明在A店一次性购买这种钢笔3支需付款 元,一次性购买5支需付款 元;
(2)设小明在A店一次性购买这种钢笔x支(x>4),需要付款多少元?(用含x的代数式表示)
(3)B店的优惠办法是不论购买多少支钢笔,一律按零售价的8折出售.请通过计算说明,若小明一次性购买10支这种钢笔,他在哪个店购买更划算?
10.某商店从批发市场以每个a元的成本价购进50个A品牌的排球,然后每个加价b元后出售.
(1)全部售出50个排球的总利润为 元.
(2)若商店在成功售出30个排球后,决定将剩余20个排球按售价8折出售,全部售完后实际盈利比按原价售卖的盈利少多少元?请列式计算.
(3)若商店同时出售A、B两种品牌的排球,B每个售价比A多10元,小红准备买三个排球,恰好商店举行优惠活动“买三免一”,即任意买三个排球(不限品牌)则价格最低的一个排球免费,小红有哪几种购买方式?付款金额分别是多少?
11.小韩和同学们在一家快餐店吃饭,如表为快餐店的菜单:
种类 配餐 价格(元) 优惠活动
A餐 1份盖饭 20 消费满150元,减24元 消费满300元,减48元 ……
B餐 1份盖饭+1杯饮料 28
C餐 1份盖饭+1杯饮料+1份小菜 32
小韩记录大家的点餐种类,并根据菜单一次点好,已知他们所点的餐共有11份盖饭,x杯饮料和5份小菜.
(1)他们共点了 份B餐;
(2)若他们至少需要7杯饮料,要使所花费的钱数最少,则应该点几份B餐.
12.某服装厂生产一种夹克和T恤,夹克每件定价100元,T恤每件定价50元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款.现某客户要到该服装厂购买夹克30件,T恤x件(x>30).
(1)若该客户按方案①购买,需付款 元(用含x的式子表示);若该客户按方案②购买,需付款 元(用含x的式子表示);
(2)若x=40,通过计算说明按方案①、方案②哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当x=40时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并说明理由.
13.为全力做好新冠肺炎疫情防控工作,某社区计划将一块长20米,宽10米的长方形形状的空地设置为全员核酸检测点.如图,空地四周均预留宽为m米的通道,中央为长方形采样区.
(1)空地中央采样区的长为 米,宽为 米(用含m的代数式表示);
(2)如图,若将空地中央的采样区分为5个大小相同的长方形候检通道,请用代数式表示一个候检通道的宽,并计算当m=2时一个候检通道的宽.
14.“抗击新冠疫情,人人有责”,学校作为人员密集的场所,要求老师和同学们进入校门后按照要求佩戴好口罩,两江育才中学初一的鑫鑫从学校了解到,上周五这一天,七年级全体同学共使用口罩1000只,喜欢统计的鑫鑫本周统计了七年级全体同学每天的口罩使用情况,制作了如下的一个统计表,以1000只为标准,其中每天超过1000只的记为“+”,每天不足1000只的记为“﹣”,统计表格如下:
周一 周二 周三 周四 周五
﹣14 +11 ﹣20 +48 ﹣5
(1)本周哪一天七年级全体同学使用口罩最多,数量是多少只?
(2)若同学们佩戴的口罩分为两种,一种是普通医用口罩,价格为1元一只,另外一种为N95型口罩,价格为3元一只,其中本周所用的普通医用口罩的数量比N95型口罩多1020只,求本周七年级所有同学们购买口罩的总金额?
15.现要从A,B两地运送苹果到C,D两地,A、B两地果园分别有苹果60吨和40吨,C、D两地分别需要苹果70吨和30吨;已知从A、B到C、D的运价如下表:
(1)若从A果园运到C地的苹果为x吨,则从A果园运到D地的苹果为 吨,从A果园将苹果运往D地的运输费用为 元;
到C地 到D地
A果园 每吨12元 每吨15元
B果园 每吨8元 每吨10元
(2)用含x的式子表示出总运输费.
16.小明为一个长方形的生活娱乐场所提供了如下的设计方案,其中扇形的水池区和三角形的儿童娱乐区外的地方都是绿地,并且AB=a,AD=b,AF=AB.
(1)用含a,b的式子表示绿地的面积;
(2)若长宽之间满足a=2b,这个生活娱乐场所需要绿地面积占总面积的以上,那么小明的设计方案符合要求吗?试说明理由.
17.某市居民使用自来水按如下标准收费:若每户月用水不超过12m3,按a元/m3收费;若超过12m3,但不超过20m3,则超过部分按1.5a元m3收费;若超过20m3,超过部分按2a元/m3收费.
户月用水量/m3 10 16 n(n>20)
收费金额/元 10a
(1)若某月用水量为16m3,收费金额为 元(用含a的式子表示);
(2)列式表示月用水量为n(n>20)m3时的收费金额.
18.为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如表(注:水费按一个月结算一次):请根据价目表的内容解答下列问题:
每月用水量(m3) 单价(元/m3)
不超出26m3的部分 3
超出26m3不超出34m3的部分 4
超出34m3的部分 7
(1)填空:若该户居民1月份用水20立方米,则应收水费 元;若该户2月份用水30立方米,则应收水费 元;
(2)若该户居民3月份用水x立方米(其中26<x≤34),则应收水费多少元?(结果用含x的代数式表示)
(3)若该户居民3月份用水a立方米(其中a>34),则应收水费多少元?(结果用含a的代数式表示)
19.为丰富第二课堂活动,学校增设了羽毛球社团.计划为羽毛球社团每位成员购买某品牌羽毛球拍1支、羽毛球3筒,并购羽毛球40筒作为社团备用球.经了解,该品牌羽毛球拍定价为100元/支,羽毛球20元/筒.现有甲、乙两家体育用品商店经销该品牌产品,均有优惠促销.甲商店促销方法是买一支羽毛球拍送一筒羽毛球;乙商店则是所有商品都按90%付款.设参加羽毛球社团的同学为x名,根据题意完成下列问题.
(1)购买方案一:全部到甲商店购买,需要支付 元,
购买方案二:全部到乙商店购买,需要支付 元;
(2)当x=15,请通过计算说明采用(1)中的哪个方案较为优惠;
(3)当x=30,聪明的你能否根据甲、乙两商店的促销信息,找到一种比(1)中两个方案更优惠的购买方法,请写出方案并列式求出所需费用,同时直接写出分别比采用(1)中两种方案各省多少钱.
20.为报名参加泉州台商投资区运动会首届羽毛球比赛项目,某校羽毛球队需要购买6支羽毛球拍和x盒羽毛球(x>6),羽毛球拍市场价为150元/支,羽毛球为30元/盒,以下是泉州台商投资区本地的两家商场提供竞标方案:
甲商场竞标方案为:所有商品九折.
乙商场竞标方案为:买1支羽毛球拍送1盒羽毛球,其余原价销售.请你根据两家商场提供的竞标方案完成下列问题:
(1)分别用含x的代数式表示在甲商场和乙商场购买所有物品的费用.
(2)当x=20时,请通过计算说明选择哪个商场购买比较省钱.
(3)当x=20时,请根据两家商场所提供的竞标方案,拟出一种折中的新方案,通过计算说明你设计的新方案所需的费用最少,并求出新方案的费用.
21.如图1.在数轴上点M表示的数为m,点N表示的数为n,点M到点N的距离记为MN.
如图2:在数轴上点A表示数a,点B表示数b,点C表示数c,a是3的相反数,b是最大的负整数,c是多项式2x3y2﹣3x+1的次数.
(1)a= ,b= ,c= ;
(2)若将数轴折叠,使得A点与C点重合,求与点B重合的点表示的数;
(3)点A、B、C开始在数轴上运动,若点B以每秒1个单位长度的速度向左运动,同时,点A和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,运动时间为t秒;
探究:3BC﹣4AB的值是否随着时间的变化而改变?若变化,请说明理由;若不变,请求其值.
参考答案
1.解:(1)他开始出现错误是在第①步,
故答案为:①;
(2)原式=5a2﹣2a﹣1﹣12+8a﹣4a2
=a2+6a﹣13.
2.解:(1)原式=4xy2+6xy﹣8xy+4﹣(﹣2xy2﹣2xy)
=4xy2﹣2xy+4+2xy2+2xy
=6xy2+4,
由题意可知:x=﹣,y+1=±2,
∴x=﹣,y=1或﹣3,
当x=﹣,y=1时,
原式=6×(﹣)×1+4
=﹣3+4
=1,
当x=﹣,y=﹣3时,
原式=6×(﹣)×9+4
=﹣27+4
=﹣23.
(2)原式=﹣4x2﹣y2+2x2﹣6x+y2
=﹣2x2﹣6x,
∵x2+3x+4=1,
∴x2+3x=﹣3,
∴原式=﹣2(x2+3x)
=﹣2×(﹣3)
=6.
3.解:原式=2a3﹣6ab+6+a3+kab
=3a3+(k﹣6)ab+6,
由题意可知:k﹣6=0,
∴k=6.
4.解:(1)3A﹣2B
=3(x2+xy+3y)﹣2(x2﹣xy)
=3x2+3xy+9y﹣2x2+2xy
=x2+5xy+9y,
由题意可知:x﹣3=0,y+5=0,
∴x=3,y=﹣5,
∴原式=9+5×3×(﹣5)+9×(﹣5)
=9﹣75﹣45
=﹣111.
(2)3A﹣2B=x2+5xy+9y
=x2+(5x+9)y,
令5x+9=0,
∴x=﹣.
5.解:(1)∵A﹣2B=﹣7x2+10x+12,B=4x2﹣5x﹣6,
∴A=(﹣7x2+10x+12)+2B
=﹣7x2+10x+12+2(4x2﹣5x﹣6)
=﹣7x2+10x+12+8x2﹣10x﹣12
=x2;
(2)A+2B
=x2+2(4x2﹣5x﹣6)
=x2+8x2﹣10x﹣12
=9x2﹣10x﹣12;
当x=﹣3时,
A+2B
=9×(﹣3)2﹣10×(﹣3)﹣12
=9×9+30﹣12
=81+30﹣12
=99.
6.解:(1)由题意可得:M﹣N=3m2﹣2m﹣5,
则M﹣(2m2﹣3m﹣2)=3m2﹣2m﹣5,
故M=3m2﹣2m﹣5+2m2﹣3m﹣2
=5m2﹣5m﹣7;
(2)由(1)得:M+N=5m2﹣5m﹣7+2m2﹣3m﹣2
=7m2﹣8m﹣9.
7.解:(1)原式=(2b2﹣ab)﹣2(b2+4ab﹣5)
=2b2﹣ab﹣2b2﹣8ab+10
=﹣9ab+10,
当ab=﹣1时,
原式=﹣9×(﹣1)+10=9+10=19;
(2)2B﹣3C
=2(b2+4ab﹣5)﹣3(﹣2b2﹣mab+3)
=2b2+8ab﹣10+6b2+3mab﹣9
=8b2+(8+3m)ab﹣19,
∵2B﹣3C的值不含ab的项,
∴8+3m=0,
解得m=,
即m的值为:.
8.解:(1)当a=7,b=3时,a2﹣b2=49﹣9=40,
(a+b)(a﹣b)=10×4=40,
故答案为:40,40;
(2)当a=﹣2,b=﹣5时,a2﹣b2=4﹣25=﹣21,
(a+b)(a﹣b)=(﹣7)×3=﹣21,
故答案为:﹣21,﹣21;
(3)通过(1)(2)中代数式的值,可知a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(4)根据(3)中的规律,可得20222﹣20212=(2022+2021)×(2022﹣2021)=4043.
9.解:(1)在A店一次性购买这种钢笔3支需付款3×10=30(元),一次性购买5支需付款4×10+(5﹣4)×10×0.6=46(元),
故答案为:30,46;
(2)∵4×10+(x﹣4)×10×0.6=6x+16,
∴在A店一次性购买这种钢笔x支(x>4),需要付款(6x+16)元;
(3)一次性购买10支这种钢笔,在A店需要付款6x+16=6×10+16=76(元),
在B店需要付款10×10×0.8=80(元),
∵76<80,
∴他在A店购买更划算.
10.解:(1)根据题意得:全部售出50个排球的总利润为50b元.
故答案为:50b;
(2)根据题意得:50b﹣30b﹣20[0.8(a+b)﹣a]
=50b﹣30b﹣20[0.8a+0.8b﹣a]
=50b﹣30b﹣20[0.8b﹣0.2a]
=50b﹣30b﹣16b+4a
=(4a+4b)元.
答:全部售完后实际盈利比按原价售卖的盈利少(4a+4b)元;
(3)设小红购买x个A品牌的排球,则购买(3﹣x)个B品牌的排球,
∵x,(3﹣x)均为自然数,
∴x可以为0,1,2,3,
∴小红共有4种购买方案,
方案1:购买3个A品牌的排球,付款金额为2(a+b)元;
方案2:购买2个A品牌的排球,1个B品牌的排球,付款金额为(a+b)+(a+b+10)=(2a+2b+10)元;
方案3:购买1个A品牌的排球,2个B品牌的排球,付款金额为2(a+b+10)元;
方案4:购买3个B品牌的排球,付款金额为2(a+b+10)元.
11.解:(1)由题意得:B餐的份数为:x﹣5,
故答案为:(x﹣5);
(2)A餐的份数为:11﹣x,
B餐的份数为:x﹣5,
则所花费的钱数为:20(11﹣x)+28(x﹣5)+32×5
=220﹣20x+28x﹣140+160
=6x+240,
∵至少需要7杯饮料,
∴当x=7时,所花费的钱数是:6×7+240=282(元),
则所点的B餐的份数为:7﹣5=2(份).
答:应该点2份B餐.
12.解:(1)按方案①购买,需付款100×30+50(x﹣30)=(50x+1500)元,
按方案②购买,需付款100×0.8×30+50×0.8x=(40x+2400)元,
故答案为:(50x+1500),(40x+2400);
(2)若x=40时,选择方案①购买较为合算,理由如下:
方案①共需付款:1500+50x=1500+50×40=3500(元),
方案②共需付款:2400+40x=2400+40×40=4000(元).
故选择方案①购买较为合算;
(3)按方案①购买夹克30件,再按方案②购买T恤10件更为省钱,理由如下:
方案①共需付款:1500+50x=1500+50×40=3500(元),
方案②共需付款:2400+40x=2400+40×40=4000(元).
按方案①购买夹克30件,再按方案②购买T恤10件共需付款:1500+50×30+10×50×80%=3400(元),
∵3400<3500<4000,
∴按方案①购买夹克30件,再按方案②购买T恤10件更为省钱.
13.解:(1)原长方形的长为20米,宽为10米,在四周均预留宽为m米的通道后,
中央核酸检测区的长为(20﹣2m)米,宽为(10﹣2m)米,
故答案为:(20﹣2m),(10﹣2m);
(2)将中央核酸检测区的“长”平均分成5份为,;
当m=2时,==3.2(米),
答:一个候检通道的宽为米,当m=2时一个候检通道的宽为3.2米.
14.解:(1)由题意得﹣20<﹣14<﹣5<+11<+48,
48+1000=1048(只),
答:本周周四这天七年级同学使用口罩最多,数量是1048只;
(2)本周共使用口罩数量为:1000×5+(﹣14+11﹣20+48﹣5)
=5000+20
=5020(只),
设本周使用N95型口罩x只,
得x+x+1020=5020,
解得x=2000,
∴x+1020=2000+1020=3020(只),
∴1×3020+3×2000
=3020+6000
=9020(元),
答:本周七年级所有同学们购买口罩的总金额为9020元.
15.解:(1)∵从A果园运到C地的苹果为x吨,
∴从A果园运到D地的苹果为(60﹣x)吨,从B果园运到C地的苹果为(70﹣x)吨,运到D地的苹果为15(60﹣x)=(900﹣15x)吨,
故答案为:(60﹣x),(900﹣15x);
(2)总运输费为12x+15(60﹣x)+8(70﹣x)+10(x﹣30)
=12x+900﹣15x+560﹣8x+10x﹣300
=﹣x+1160(元).
16.解:(1)绿地的面积为:ab﹣a ﹣πb2=ab﹣πb2;
(2)当a=2b时,
绿地面积为:ab﹣πb2=(﹣π)b2,
(﹣π)b2÷2b2=<,
所以小明的设计方案不符合要求.
17.解:(1)当用水量为16m3时.
12a+1.5a(16﹣12)=12a+6a=18a.
答:月用水量为16m3时,收费金额为18a元.
(2)当用水量为nm3时.
12a+1.5a(20﹣12)+2a(n﹣20)
=12a+12a+2na﹣40a
=(2na﹣16a)m3
答:月用水量为n(n>20)m3时的收费(2na﹣16a)m3.
18.解:(1)3×20=60(元),
3×26+4×(30﹣26)
=3×26+4×4
=78+16
=94(元).
故答案为:60;94.
(2)依题意得:应收水费为3×26+4×(x﹣26)=(4x﹣26)元.
故应收水费(4x﹣26)元;
(3)依题意得:应收水费为3×26+4×(34﹣26)+7(a﹣34)=(7a﹣128)元.
故应收水费(7a﹣128)元.
19.解:(1)甲商店购买需付款:100x+(3x﹣x+40)×20=140x+800(元),
乙商店购买需付款90%×100x+20×90%(3x+40)=144x+720(元),
故答案为:(140x+800),(144x+720);
(2)当x=15时,
甲商店需:140×15+800=2900(元),
乙商店需:144×15+720=2880(元),
因为2900>2880,
所以乙商店购买合算;
(3)先在甲商店购买30支球拍,送30筒球需3000元,剩下100筒球在乙商店购买需1800元,共需4800元,
甲商店购买需:140×30+800=5000(元),
乙商店购买需:144×30+720=5040(元),
5000﹣4800=200(元),5040﹣4800=240(元),
比甲商店省200元,比乙商店省240元.
20.解:(1)在甲商场购买所有物品的费用为:0.9(6×150+30x)=(27x+810)(元),
在乙商场购买所有物品的费用为:6×150+30(x﹣6)=(30x+720)(元);
(2)当x=20时,27x+810=1350(元);
30x+720=1320(元);
1350>1320,
答:选择乙商场购买比较省钱.
(3)当x=20时,
在乙商场购买6支羽毛球拍和6盒羽毛球的费用为:
6×150=900(元);
在甲商场购买14盒羽毛球的费用为:
30×14×0.9=378(元);
合计的费用为:900+378=1278(元).
所以在甲商场购买14盒羽毛球、在乙商场购买6支羽毛球拍和6盒羽毛球费用最少,只要1278元.
21.解:(1)∵a是3的相反数,b是最大的负整数,c是多项式2x3y2﹣3x+1的次数,
∴a=﹣3,b=﹣1,c=5,
故答案为:﹣3,﹣1,5;
(2)当﹣3与5重合时,折叠点是1,
∴1﹣(﹣1)=2,1+2=3,
故与点B重合的点表示的数是3;
(3)A:﹣3+2t,B:﹣1﹣t,C:5+3t,
∴BC=(5+3t)﹣(﹣1﹣t)=6+4t,
AB=(﹣1﹣t)﹣(﹣3+2t)=2﹣3t,
∴3BC﹣4AB=3(6+4t)﹣4(2﹣3t)=10;
答:3BC﹣4AB=10是定值,不随着时间的变化而改变.
