【高考专辑】【专题33】2015年高三数学(理)【押题精练】活用审题,破解高考
文档属性
| 名称 | 【高考专辑】【专题33】2015年高三数学(理)【押题精练】活用审题,破解高考 |  | |
| 格式 | zip | ||
| 文件大小 | 541.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-14 16:25:39 | ||
图片预览






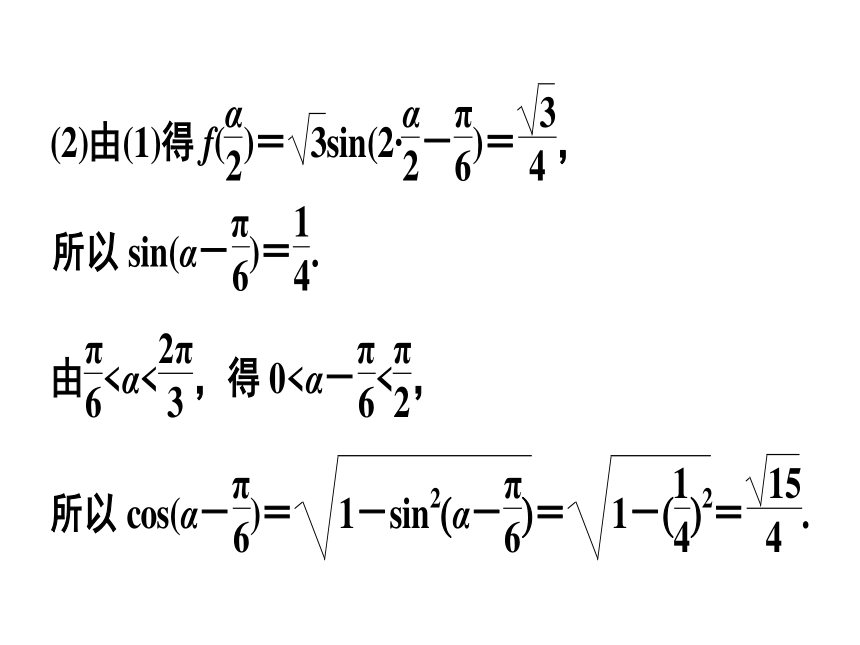
文档简介
课件81张PPT。专题33
活用审题,破解高考天津南开市2015届高三活用审题,破解高考思 想 方 法 概 述热 点 分 类 突 破真 题 与 押 题 审题是解题的开端,深入细致的审题是成功解题的必要前提.著名数学教育家波利亚说,“最糟糕的情况就是学生没有弄清问题就进行演算和作图.”为此波利亚总结出一张“怎样解题表”,将解题的过程分为四个阶段.其中第一步弄清问题就是我们常说的审题.审题就是多角度地观察,由表及里,由条件到结论,由数式到图形,洞察问题实质,选择正确的解题方向.事实上,很多考生往往对审题掉以轻心,或不知从何处入手进行审题,致使解题失误而丢分,真是令人痛心不已.本讲结合实例,教你正确的审题方法,给你制订一条“审题路线图”,破解高考不再难. 四审结构定方案一审条件挖隐含二审结论会转换三审图形抓特点六审细节更完善五审图表、数据找规律目录页5任何一个数学问题都是由条件和结论两部分构成的.条件是解题的主要素材,充分利用条件间的内在联系是解题的必经之路.条件有明示的,有隐含的,审视条件更重要的是要充分挖掘每一个条件的内涵和隐含的信息,发挥隐含条件的解题功能.一审条件挖隐含例1 (2014·重庆)已知函数f(x)= sin(ωx+φ)(ω>0,- ≤φ< )的图象关于直线x= 对称,且图象上相邻两个最高点的距离为π.
(1)求ω和φ的值;
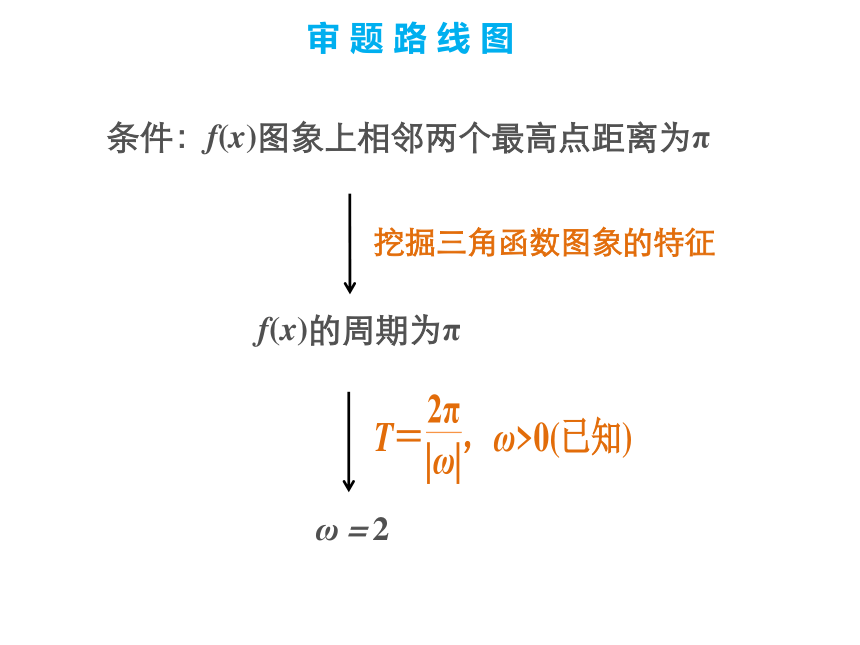
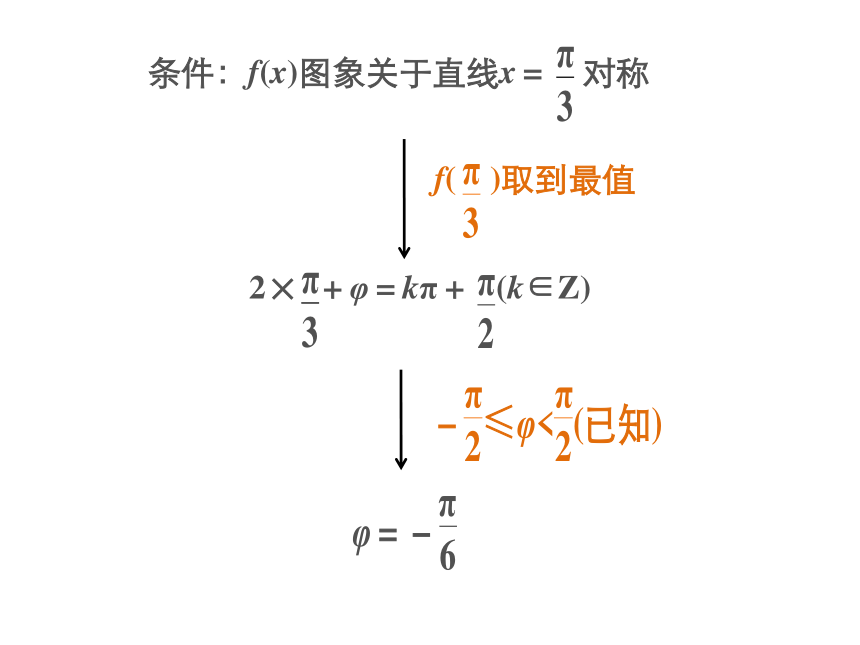
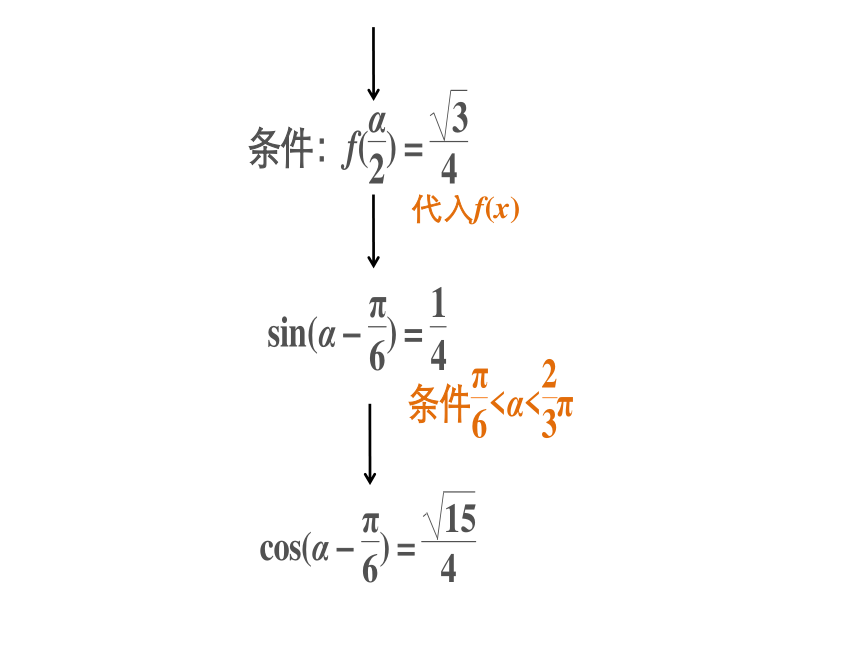
(2)若f( )= ( <α< ),求cos(α+ )的值.条件:f(x)图象上相邻两个最高点距离为π审 题 路 线 图挖掘三角函数图象的特征f(x)的周期为πω=2条件:f(x)图象关于直线x= 对称f( )取到最值2× +φ=kπ+ (k∈Z)代入f(x)解 (1)因为f(x)的图象上相邻两个最高点的距离为π,所以f(x)的最小正周期为T=π,从而ω= =2.变式训练 1 (2014·四川)已知函数f(x)=sin(3x+ ).
(1)求f(x)的单调递增区间;
(2)若α是第二象限角,f( )= cos(α+ )cos 2α,求cos α-sin α的值.解 (1)因为函数y=sin x的单调递增区间为[- +2kπ,
+2kπ],k∈Z,由- +2kπ≤3x+ ≤ +2kπ,k∈Z,当sin α+cos α=0时,由α是第二象限角,知α=
+2kπ,k∈Z.此时,cos α-sin α=- .由α是第二象限角,知cos α-sin α<0,当sin α+cos α≠0时,有(cos α-sin α)2= .此时cos α-sin α=- .综上所述,cos α-sin α=- 或- .问题解决的最终目标就是求出结论或说明已给结论正确或错误.因而解决问题时的思维过程大多都是围绕着结论这个目标进行定向思考的.审视结论,就是在结论的启发下,探索已知条件和结论之间的内在联系和转化规律.善于从结论中捕捉解题信息,善于对结论进行转化,使之逐步靠近条件,从而发现和确定解题方向.二审结论会转换例2 已知函数f(x)= x2+aln x.
(1)若a=-1,求函数f(x)的极值,并指出是极大值还是极小值;
(2)若a=1,求函数f(x)在[1,e]上的最大值和最小值;
(3)若a=1,求证:在区间[1,+∞)上,函数f(x)的图象在函数g(x)= x3的图象的下方.审 题 路 线 图(从结论出发向条件转化,注意隐含条件——定义域)求f(x)的极值求f′(x)=0的解,即f(x)的极值点(转化为求函数值)将极值点代入f(x)求对应的极大、极小值(转化为研究单调性)求f(x)在[1,e]上的单调性(转化为求函数值)比较端点值、极值,确定最大、最小值(构造函数进行转化)F(x)=f(x)-g(x)(将图象的上、下关系转化为数量关系)求证F(x)<0在[1,+∞)上恒成立.研究函数F(x)在[1,+∞)上的单调性.(1)解 由于函数f(x)的定义域为(0,+∞),令f′(x)=0得x=1或x=-1(舍去),
当x∈(0,1)时,函数f(x)单调递减,
当x∈(1,+∞)时,函数f(x)单调递增,所以f(x)在x=1处取得极小值为 .(2)解 当a=1时,易知函数f(x)在[1,e]上为增函数,当x>1时,F′(x)<0,
故f(x)在区间[1,+∞)上是减函数,又F(1)=- <0,所以在区间[1,+∞)上,F(x)<0恒成立.
即f(x)因此,当a=1时,在区间[1,+∞)上,函数f(x)的图象在函数g(x)的图象的下方.变式训练 2 (2014·课标全国Ⅰ)设函数f(x)=aln x+ x2-bx(a≠1),曲线y=f(x)在点(1,f(1))处的切线斜率为0.
(1)求b;
(2)若存在x0≥1,使得f(x0)< ,求a的取值范围.解 (1)f′(x)= +(1-a)x-b.
由题设知f′(1)=0,解得b=1.
(2)f(x)的定义域为(0,+∞),由(1)知,f(x)=aln x+ x2-x,故当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)单调递增.所以不合题意.在不少数学高考试题中,问题的条件往往是以图形的形式给出,或将条件隐含在图形之中,因此在审题时,要善于观察图形,洞悉图形所隐含的特殊关系、数值的特点、变化的趋势.抓住图形的特征,运用数形结合的数学思想方法,是破解考题的关键.三审图形抓特点例3 已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|< ),y=f(x)的部分图象如图所示,则f( )=________.审 题 路 线 图f(x)图象的周期性ω=2f(x)图象过点( π,0)Atan(2× π+φ)=0 π+φ=kπ,k∈Z|φ|<φ=f(x)图象过点(0,1)A=1又|φ|< ,所以φ= .又图象过定点(0,1),所以A=1.综上可知,f(x)=tan(2x+ ),变式训练3 如图,在△ABC中,AB=3,AC=5,若O为△ABC的外心,则 的值为________.解析 方法一 取边BC的中点D,由于O为△ABC的外心,所以 ⊥ ,方法二 取AB的中点E,AC的中点F,
连接OE,OF,则OE⊥AB,OF⊥AC.答案 8数学问题中的条件和结论,很多都是以数式的结构形式进行搭配和呈现的.在这些问题的数式结构中,往往都隐含着某种特殊关系,认真审视数式的结构特征,对数式结构进行深入分析,加工转化,可以寻找到突破问题的方案.四审结构定方案例4 在锐角△ABC中,角A、B、C的对边分别为a、b、c.若
=6cos C,则 的值是________.审 题 路 线 图(数式中既有边又有角,应统一)〈观察方向一〉
观察条件: =6cos C(将条件转化为简洁形式)观察结论所求:(考虑到在△ABC中的正、余弦定理,切化
弦是必由之路)(角化边、用条件)(关注数式的特征)〈观察方向二〉
观察条件: =6cos C角A、B具有轮换性边a、b具有轮换性
观察所求结论:(从数式的特征考虑)(特殊化思想,可靠吗?)(完全转化成三角函数运算)当A=B即a=b时,应满足题意根据正、余弦定理得答案 4变式训练 4 (1)(2014·课标全国Ⅰ)已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)·(sin A-sin B)=(c-b)·sin C,则△ABC面积的最大值为________.
(2)(2014·课标全国Ⅱ)函数f(x)=sin(x+2φ)-2sin φ·
cos(x+φ)的最大值为________.又(2+b)·(sin A-sin B)=(c-b)sin C可化为(a+b)(a-b)=(c-b)·c,∴a2-b2=c2-bc,∴b2+c2-a2=bc.∴△ABC中,4=a2=b2+c2-2bc·cos 60°=b2+c2-bc≥2bc-bc=bc(“=”当且仅当b=c时取得),(2)∵f(x)=sin(x+2φ)-2sin φcos(x+φ)
=sin[(x+φ)+φ]-2sin φcos(x+φ)
=sin(x+φ)cos φ+cos(x+φ)sin φ-2sin φcos(x+φ)
=sin(x+φ)cos φ-cos(x+φ)sin φ
=sin[(x+φ)-φ]=sin x,
∴f(x)的最大值为1.(2)1答案 (1) 题目中的图表、数据包含着问题的基本信息,往往也暗示着解决问题的目标和方向.在审题时,要认真观察分析图表、数据的特征和规律,常常可以找到解决问题的思路和方法.五审图表、数据找规律例5 下表中的数阵为“森德拉姆素数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为ai,j(i,j∈N*),则
(1)a9,9=________;
(2)表中的数82共出现________次.审 题 路 线 图每行成等差数列审视图表数据(ai,j)a1,j=j+1(a1,1=2,d=1)a1,9=10每列成等差数列a9,9=a1,9+8×9=10+72=82一般规律观察ai,j=(i+1)+(j-1)·i=ij+1数82在表中位置ai,j=82=ij+1ij+1=82的解82出现的次数解析 (1)a9,9表示第9行第9列,第1行的公差为1,
第2行的公差为2,……,第9行的公差为9,
第9行的首项b1=10,则b9=10+8×9=82;
(2)第1行数组成的数列a1,j(j=1,2,…)是以2为首项,公差为1的等差数列,
所以a1,j=2+(j-1)·1=j+1;第i行数组成的数列ai,j(j=1,2,…)是以i+1为首项,公差为i的等差数列,
所以ai,j=(i+1)+(j-1)i=ij+1,
由题意得ai,j=ij+1=82,即ij=81,且i,j∈N*,
所以81=81×1=27×3=9×9=1×81=3×27,
故表格中82共出现5次.答案 (1)82(2)5变式训练 5 (1)将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,数列第6项a6=________;第n项an=________.解析 由已知的图形我们可以得出图形的编号与图中石子的个数之间的关系为n=1时,a1=2+3= ×(2+3)×2;n=2时,a2=2+3+4= ×(2+4)×3;由此我们可以推断:an=2+3+…+(n+2)= ×
[2+(n+2)]×(n+1)= ,∴a6=35.(2)如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为( )
A.11 B.11.5 C.12 D.12.5解析 中位数是把频率分布直方图分成两个面积相等部分的平行于纵轴的直线横坐标.
设中位数为a,则x=a将频率分布直方图分成两个面积相等的部分,
则有0.30+(a-10)×0.1=0.5,所以a=12.答案 C审题不仅要从宏观上、整体上去分析、去把握,还要更加注意审视一些细节上的问题.例如括号内的标注、数据的范围、图象的特点等.因为标注、范围大多是对数学概念、公式、定理中所涉及的一些量或解析式的限制条件.审视细节能适时地利用相关量的约束条件,调整解决问题的方向.所以说重视审视细节,更能体现审题的深刻性.六审细节更完善审 题 路 线 图(注意n∈N*,an>0)a1=2(下面的变形是有条件的,条件是n≥2)(不变形怎么办?肯定要进行代数式变形)(an+an-1)(an-an-1-2)=0(注意到an>0了吗?an+an-1>0)an-an-1=2(关于等差数列的定义不用重复了吧!)an=2+(n-1)×2=2n(注意到bn与an的关系了吗?n是分奇偶的)b1=a1=2;b2=b1=2;b3=a3=6;b4=b2=2(cn与bn的关系很特殊!)c1=b6=b3=6c2=b8=b4=2(下面变化的条件是n≥3,这可是细节啊!)Tn=c1+c2+c3+…+cn
=6+2+(22+2)+(23+2)+…+(2n-1+2)
=2n+2n(不要忘了当n=1,n=2时,对Tn的表达式的验证)因为a1>0,故a1=2;
当n≥2时,an=Sn-Sn-1即(an+an-1)(an-an-1-2)=0.
因为an>0,所以an-an-1=2,即{an}为等差数列,
所以an=2n (n∈N*).(2)c1=b6=b3=a3=6,c2=b8=b4=b2=b1=a1=2,n≥3时,此时,Tn=8+(22+2)+(23+2)+…+(2n-1+2)=2n+2n;当n=2时,T2=22+2×2=8=c1+c2.点评 从审题路线图可以看出,细节对思维的方向不断地修正着.变式训练6 (2014·浙江)已知数列{an}和{bn}满足a1a2a3…an=( ) (n∈N*).若{an}为等比数列,且a1=2,b3=6+b2.
(1)求an与bn;
(2)设cn= (n∈N*).记数列{cn}的前n项和为Sn.
①求Sn;
②求正整数k,使得对任意n∈N*,均有Sk≥Sn.解 (1)由题意知a1a2a3…an=( ) ,b3-b2=6,
知a3=( ) =8.又由a1=2,得公比q=2(q=-2舍去),
所以数列{an}的通项为an=2n(n∈N*),故数列{bn}的通项为bn=n(n+1)(n∈N*).所以,a1a2a3…an= = .②因为c1=0,c2>0,c3>0,c4>0,所以,当n≥5时,cn<0.
综上,对任意n∈N*恒有S4≥Sn,故k=4.1.解题先审题,养成认真审题,缜密思考的良好习惯.规律总结2.审题要慢要细,要谨慎思考:(1)全部的条件和结论;(2)必要的图形和图表;(3)数学式子和数学符号.要善于捕捉题目中的有效信息,要有较强的洞察力和显化隐含条件的能力.要制订和用好审题路线图.3.审题路线图:
→ →
→ →
→ .一审条件挖隐含二审结论会转换三审图形抓特点四审结构定方案五审图表、数据找规律六审细节更完善
活用审题,破解高考天津南开市2015届高三活用审题,破解高考思 想 方 法 概 述热 点 分 类 突 破真 题 与 押 题 审题是解题的开端,深入细致的审题是成功解题的必要前提.著名数学教育家波利亚说,“最糟糕的情况就是学生没有弄清问题就进行演算和作图.”为此波利亚总结出一张“怎样解题表”,将解题的过程分为四个阶段.其中第一步弄清问题就是我们常说的审题.审题就是多角度地观察,由表及里,由条件到结论,由数式到图形,洞察问题实质,选择正确的解题方向.事实上,很多考生往往对审题掉以轻心,或不知从何处入手进行审题,致使解题失误而丢分,真是令人痛心不已.本讲结合实例,教你正确的审题方法,给你制订一条“审题路线图”,破解高考不再难. 四审结构定方案一审条件挖隐含二审结论会转换三审图形抓特点六审细节更完善五审图表、数据找规律目录页5任何一个数学问题都是由条件和结论两部分构成的.条件是解题的主要素材,充分利用条件间的内在联系是解题的必经之路.条件有明示的,有隐含的,审视条件更重要的是要充分挖掘每一个条件的内涵和隐含的信息,发挥隐含条件的解题功能.一审条件挖隐含例1 (2014·重庆)已知函数f(x)= sin(ωx+φ)(ω>0,- ≤φ< )的图象关于直线x= 对称,且图象上相邻两个最高点的距离为π.
(1)求ω和φ的值;
(2)若f( )= ( <α< ),求cos(α+ )的值.条件:f(x)图象上相邻两个最高点距离为π审 题 路 线 图挖掘三角函数图象的特征f(x)的周期为πω=2条件:f(x)图象关于直线x= 对称f( )取到最值2× +φ=kπ+ (k∈Z)代入f(x)解 (1)因为f(x)的图象上相邻两个最高点的距离为π,所以f(x)的最小正周期为T=π,从而ω= =2.变式训练 1 (2014·四川)已知函数f(x)=sin(3x+ ).
(1)求f(x)的单调递增区间;
(2)若α是第二象限角,f( )= cos(α+ )cos 2α,求cos α-sin α的值.解 (1)因为函数y=sin x的单调递增区间为[- +2kπ,
+2kπ],k∈Z,由- +2kπ≤3x+ ≤ +2kπ,k∈Z,当sin α+cos α=0时,由α是第二象限角,知α=
+2kπ,k∈Z.此时,cos α-sin α=- .由α是第二象限角,知cos α-sin α<0,当sin α+cos α≠0时,有(cos α-sin α)2= .此时cos α-sin α=- .综上所述,cos α-sin α=- 或- .问题解决的最终目标就是求出结论或说明已给结论正确或错误.因而解决问题时的思维过程大多都是围绕着结论这个目标进行定向思考的.审视结论,就是在结论的启发下,探索已知条件和结论之间的内在联系和转化规律.善于从结论中捕捉解题信息,善于对结论进行转化,使之逐步靠近条件,从而发现和确定解题方向.二审结论会转换例2 已知函数f(x)= x2+aln x.
(1)若a=-1,求函数f(x)的极值,并指出是极大值还是极小值;
(2)若a=1,求函数f(x)在[1,e]上的最大值和最小值;
(3)若a=1,求证:在区间[1,+∞)上,函数f(x)的图象在函数g(x)= x3的图象的下方.审 题 路 线 图(从结论出发向条件转化,注意隐含条件——定义域)求f(x)的极值求f′(x)=0的解,即f(x)的极值点(转化为求函数值)将极值点代入f(x)求对应的极大、极小值(转化为研究单调性)求f(x)在[1,e]上的单调性(转化为求函数值)比较端点值、极值,确定最大、最小值(构造函数进行转化)F(x)=f(x)-g(x)(将图象的上、下关系转化为数量关系)求证F(x)<0在[1,+∞)上恒成立.研究函数F(x)在[1,+∞)上的单调性.(1)解 由于函数f(x)的定义域为(0,+∞),令f′(x)=0得x=1或x=-1(舍去),
当x∈(0,1)时,函数f(x)单调递减,
当x∈(1,+∞)时,函数f(x)单调递增,所以f(x)在x=1处取得极小值为 .(2)解 当a=1时,易知函数f(x)在[1,e]上为增函数,当x>1时,F′(x)<0,
故f(x)在区间[1,+∞)上是减函数,又F(1)=- <0,所以在区间[1,+∞)上,F(x)<0恒成立.
即f(x)
(1)求b;
(2)若存在x0≥1,使得f(x0)< ,求a的取值范围.解 (1)f′(x)= +(1-a)x-b.
由题设知f′(1)=0,解得b=1.
(2)f(x)的定义域为(0,+∞),由(1)知,f(x)=aln x+ x2-x,故当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)单调递增.所以不合题意.在不少数学高考试题中,问题的条件往往是以图形的形式给出,或将条件隐含在图形之中,因此在审题时,要善于观察图形,洞悉图形所隐含的特殊关系、数值的特点、变化的趋势.抓住图形的特征,运用数形结合的数学思想方法,是破解考题的关键.三审图形抓特点例3 已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|< ),y=f(x)的部分图象如图所示,则f( )=________.审 题 路 线 图f(x)图象的周期性ω=2f(x)图象过点( π,0)Atan(2× π+φ)=0 π+φ=kπ,k∈Z|φ|<φ=f(x)图象过点(0,1)A=1又|φ|< ,所以φ= .又图象过定点(0,1),所以A=1.综上可知,f(x)=tan(2x+ ),变式训练3 如图,在△ABC中,AB=3,AC=5,若O为△ABC的外心,则 的值为________.解析 方法一 取边BC的中点D,由于O为△ABC的外心,所以 ⊥ ,方法二 取AB的中点E,AC的中点F,
连接OE,OF,则OE⊥AB,OF⊥AC.答案 8数学问题中的条件和结论,很多都是以数式的结构形式进行搭配和呈现的.在这些问题的数式结构中,往往都隐含着某种特殊关系,认真审视数式的结构特征,对数式结构进行深入分析,加工转化,可以寻找到突破问题的方案.四审结构定方案例4 在锐角△ABC中,角A、B、C的对边分别为a、b、c.若
=6cos C,则 的值是________.审 题 路 线 图(数式中既有边又有角,应统一)〈观察方向一〉
观察条件: =6cos C(将条件转化为简洁形式)观察结论所求:(考虑到在△ABC中的正、余弦定理,切化
弦是必由之路)(角化边、用条件)(关注数式的特征)〈观察方向二〉
观察条件: =6cos C角A、B具有轮换性边a、b具有轮换性
观察所求结论:(从数式的特征考虑)(特殊化思想,可靠吗?)(完全转化成三角函数运算)当A=B即a=b时,应满足题意根据正、余弦定理得答案 4变式训练 4 (1)(2014·课标全国Ⅰ)已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且(2+b)·(sin A-sin B)=(c-b)·sin C,则△ABC面积的最大值为________.
(2)(2014·课标全国Ⅱ)函数f(x)=sin(x+2φ)-2sin φ·
cos(x+φ)的最大值为________.又(2+b)·(sin A-sin B)=(c-b)sin C可化为(a+b)(a-b)=(c-b)·c,∴a2-b2=c2-bc,∴b2+c2-a2=bc.∴△ABC中,4=a2=b2+c2-2bc·cos 60°=b2+c2-bc≥2bc-bc=bc(“=”当且仅当b=c时取得),(2)∵f(x)=sin(x+2φ)-2sin φcos(x+φ)
=sin[(x+φ)+φ]-2sin φcos(x+φ)
=sin(x+φ)cos φ+cos(x+φ)sin φ-2sin φcos(x+φ)
=sin(x+φ)cos φ-cos(x+φ)sin φ
=sin[(x+φ)-φ]=sin x,
∴f(x)的最大值为1.(2)1答案 (1) 题目中的图表、数据包含着问题的基本信息,往往也暗示着解决问题的目标和方向.在审题时,要认真观察分析图表、数据的特征和规律,常常可以找到解决问题的思路和方法.五审图表、数据找规律例5 下表中的数阵为“森德拉姆素数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为ai,j(i,j∈N*),则
(1)a9,9=________;
(2)表中的数82共出现________次.审 题 路 线 图每行成等差数列审视图表数据(ai,j)a1,j=j+1(a1,1=2,d=1)a1,9=10每列成等差数列a9,9=a1,9+8×9=10+72=82一般规律观察ai,j=(i+1)+(j-1)·i=ij+1数82在表中位置ai,j=82=ij+1ij+1=82的解82出现的次数解析 (1)a9,9表示第9行第9列,第1行的公差为1,
第2行的公差为2,……,第9行的公差为9,
第9行的首项b1=10,则b9=10+8×9=82;
(2)第1行数组成的数列a1,j(j=1,2,…)是以2为首项,公差为1的等差数列,
所以a1,j=2+(j-1)·1=j+1;第i行数组成的数列ai,j(j=1,2,…)是以i+1为首项,公差为i的等差数列,
所以ai,j=(i+1)+(j-1)i=ij+1,
由题意得ai,j=ij+1=82,即ij=81,且i,j∈N*,
所以81=81×1=27×3=9×9=1×81=3×27,
故表格中82共出现5次.答案 (1)82(2)5变式训练 5 (1)将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,数列第6项a6=________;第n项an=________.解析 由已知的图形我们可以得出图形的编号与图中石子的个数之间的关系为n=1时,a1=2+3= ×(2+3)×2;n=2时,a2=2+3+4= ×(2+4)×3;由此我们可以推断:an=2+3+…+(n+2)= ×
[2+(n+2)]×(n+1)= ,∴a6=35.(2)如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为( )
A.11 B.11.5 C.12 D.12.5解析 中位数是把频率分布直方图分成两个面积相等部分的平行于纵轴的直线横坐标.
设中位数为a,则x=a将频率分布直方图分成两个面积相等的部分,
则有0.30+(a-10)×0.1=0.5,所以a=12.答案 C审题不仅要从宏观上、整体上去分析、去把握,还要更加注意审视一些细节上的问题.例如括号内的标注、数据的范围、图象的特点等.因为标注、范围大多是对数学概念、公式、定理中所涉及的一些量或解析式的限制条件.审视细节能适时地利用相关量的约束条件,调整解决问题的方向.所以说重视审视细节,更能体现审题的深刻性.六审细节更完善审 题 路 线 图(注意n∈N*,an>0)a1=2(下面的变形是有条件的,条件是n≥2)(不变形怎么办?肯定要进行代数式变形)(an+an-1)(an-an-1-2)=0(注意到an>0了吗?an+an-1>0)an-an-1=2(关于等差数列的定义不用重复了吧!)an=2+(n-1)×2=2n(注意到bn与an的关系了吗?n是分奇偶的)b1=a1=2;b2=b1=2;b3=a3=6;b4=b2=2(cn与bn的关系很特殊!)c1=b6=b3=6c2=b8=b4=2(下面变化的条件是n≥3,这可是细节啊!)Tn=c1+c2+c3+…+cn
=6+2+(22+2)+(23+2)+…+(2n-1+2)
=2n+2n(不要忘了当n=1,n=2时,对Tn的表达式的验证)因为a1>0,故a1=2;
当n≥2时,an=Sn-Sn-1即(an+an-1)(an-an-1-2)=0.
因为an>0,所以an-an-1=2,即{an}为等差数列,
所以an=2n (n∈N*).(2)c1=b6=b3=a3=6,c2=b8=b4=b2=b1=a1=2,n≥3时,此时,Tn=8+(22+2)+(23+2)+…+(2n-1+2)=2n+2n;当n=2时,T2=22+2×2=8=c1+c2.点评 从审题路线图可以看出,细节对思维的方向不断地修正着.变式训练6 (2014·浙江)已知数列{an}和{bn}满足a1a2a3…an=( ) (n∈N*).若{an}为等比数列,且a1=2,b3=6+b2.
(1)求an与bn;
(2)设cn= (n∈N*).记数列{cn}的前n项和为Sn.
①求Sn;
②求正整数k,使得对任意n∈N*,均有Sk≥Sn.解 (1)由题意知a1a2a3…an=( ) ,b3-b2=6,
知a3=( ) =8.又由a1=2,得公比q=2(q=-2舍去),
所以数列{an}的通项为an=2n(n∈N*),故数列{bn}的通项为bn=n(n+1)(n∈N*).所以,a1a2a3…an= = .②因为c1=0,c2>0,c3>0,c4>0,所以,当n≥5时,cn<0.
综上,对任意n∈N*恒有S4≥Sn,故k=4.1.解题先审题,养成认真审题,缜密思考的良好习惯.规律总结2.审题要慢要细,要谨慎思考:(1)全部的条件和结论;(2)必要的图形和图表;(3)数学式子和数学符号.要善于捕捉题目中的有效信息,要有较强的洞察力和显化隐含条件的能力.要制订和用好审题路线图.3.审题路线图:
→ →
→ →
→ .一审条件挖隐含二审结论会转换三审图形抓特点四审结构定方案五审图表、数据找规律六审细节更完善
同课章节目录
