1.3.1勾股定理的应用 课件(21张PPT) 2023—2024学年北师大版数学八年级上册
文档属性
| 名称 | 1.3.1勾股定理的应用 课件(21张PPT) 2023—2024学年北师大版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 361.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 10:10:20 | ||
图片预览








文档简介
(共21张PPT)
1.3.1 勾股定理的应用
第一章 勾股定理
课前提问:(2分钟)
1、什么是勾股定理?用字母怎么表示?
直角三角形两直角边的平方和等于斜边的平方。如果用a、b、c
分别表示直角三角形的两直角边和斜边,那么a2+b2=c2
2、勾股定理的逆定理是什么?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
3、什么是勾股数?有哪些常见的勾股数?
满足a2 +b2=c2的三个正整数,称为勾股数.常见的勾股数:3、4、5;6、8、10;5、12、13;8,15,17;
7,24,25;9,40,41…
学习目标(1分钟)
1、掌握立体图形中圆柱体和长方体的最短线路问题的解题思路;
2、熟练运用勾股定理及其逆定理解决实际问题。
自学指导1(1分钟)
仔细阅读课本P13 “做一做”之前的内容,思考并回答下列问题:
如图,有一个圆柱体,它的高等于12cm,底面上圆的周长等于18cm。在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱体侧面爬行到B点。
3、哪条路径最短?最短路程是多少?
1、从A点沿圆柱侧面到B点有多少条路径?
答:有无数多条。
●
A
A
B
C
●
●
B
C
●
2、如将其侧面展开,A点在矩形左下角,则B点在哪?
答:B在上边的中点处。
答:线段AB最短。最短路程是15cm.
自学(3分钟)
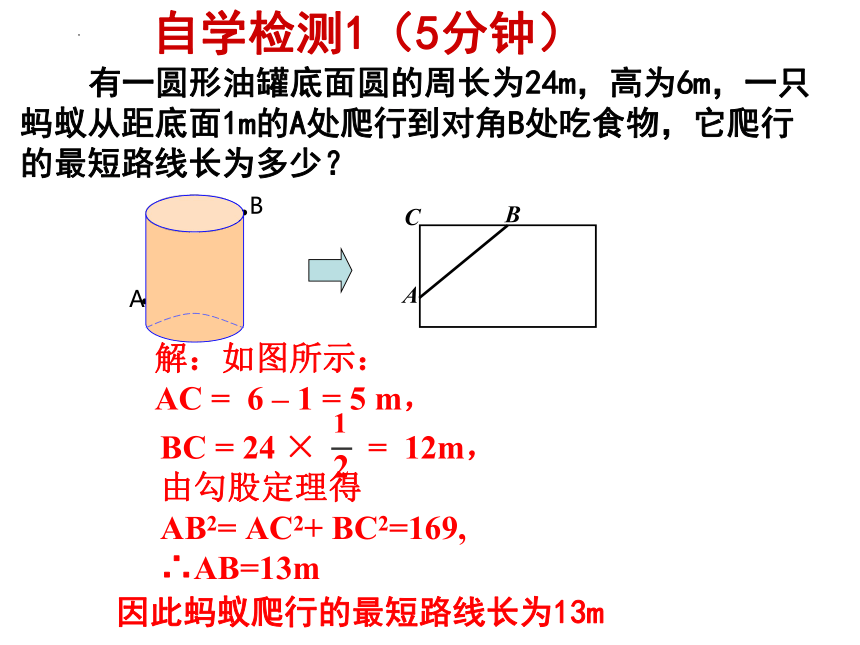
有一圆形油罐底面圆的周长为24m,高为6m,一只蚂蚁从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
A
B
解:如图所示:
AC = 6 – 1 = 5 m,
BC = 24 × = 12m,
由勾股定理得
AB2= AC2+ BC2=169,
∴AB=13m
B
A
C
2
1
自学检测1(5分钟)
因此蚂蚁爬行的最短路线长为13m
讨论、更正、点拨(2分钟)
蚂蚁怎样沿圆柱体侧面从A点爬行到B点最近?
A
B
A
B
A
B
A
B
(1)
(2)
(3)
(4)
方法点拨:圆柱体(或几何体)表面求最短路径
①展(将路径经过的侧面展开在同一平面上)
②找(在展开平面上找对应点)
③连(用线段将两对应点连接,最短路径为该线段)
④解(利用勾股定理求③ 中线段长即得解)
如图正方体棱长为a,如图一只蚂蚁从A点经正方体表面爬行到G点。
1、蚂蚁经过哪些正方体表面能从A点爬行到G点?
A
B
C
D
E
F
G
H
2、有最短路径吗?请通过计算说明?
自学指导2(1分钟)
学生自学、教师巡视(3分钟)
1、解:蚂蚁可从侧面
共6种情况从A点爬行到G点。
前
上
右
下
后
右
左
上
后
如图正方体棱长为a,如图一只蚂蚁从A点经正方体表面爬行到G点。
1、蚂蚁经过哪些正方体表面能从A点爬行到G点?
2、有最短路径吗?请通过计算说明?
自学指导2(1分钟)
学生自学、教师巡视(3分钟)
a
a
a
前
右
A
B
C
D
E
F
G
H
2、解: ①前侧面+右侧面(或左侧面+后侧面)
点拨(2分钟)正方体爬行路径(分三种情况)
正方体爬行路径三种情况都相等
d2=a2+4a2=5a2
A
B
F
E
H
G
前(后)
上(下)
(3)
d
a
a
a
a
所以,有最短路径,长的平方为5a2
前(后)
右(左)
B
C
A
E
F
G
(1)
d
a
a
a
D
A
E
H
G
F
左(右)
(2)
d
a
a
a
上(下)
A
B
C
D
E
F
G
H
●
●
解:
如把正方体变成如下图的长方体,长方体底面长为2,宽为1,高为4,蚂蚁从A点沿长方体表面爬到E点有多少种爬行可能?哪种爬行路径的距离最短?是多少?
自学检测2(4分钟)
解:长方体侧面展开图一共有三种情况,如上图,其距离分别是:
第一种:
第二种:
第三种:
D
A
G
H
F
E1
2
4
1
左(右)
上(下)
(1)
B
A
G
F
H
E2
2
4
1
前(后)
上(下)
(2)
A
B
C
F
G
E3
4
1
2
前
(后)
右(左)
(3)
AE12=22+52=29
AE22=12+62=37
AE32=32+42=25
∵AE22 > AE12>AE32
∴最短路径是AE3,距离是5
点拨:(4分钟)
长方体的最短路径d的计算方法为 d =a +(b+c) ,其中a为最大棱长。
小结:(2分钟)
一、立体图形求最短路径问题的思路:
二、正方体最短路径d计算方法
d2=a2+4a2=5a2
三、长方体最短路径d计算方法
d2=a2+(b+c)2
最大棱长
方法点拨:几何体表面求最短路径
①展(将路径经过的侧面展开在同一平面上)
②找(在展开平面上找对应点)
③连(用线段将两对应点连接,最短路径为该线段)
④解(利用勾股定理求③ 中线段长即得解)
当堂训练(14分钟)
2、如右下图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A
1.如图,一只蚂蚁从A点沿圆柱侧面爬到顶面相对的B点处,如果圆柱的高为8 cm,圆柱的半径为 cm,那么最短路径AB长( ).
D
A.8 B.6 C.平方后为208的数 D.10
12≤a≤13 B.12≤a≤15
C. 5≤a≤12 D. 5≤a≤13
A
B
O
3.如图,台阶A处的蚂蚁要爬到B处搬运食物,最近距离是 。
分析:
25
4、一个无盖的长方体形盒子的长、宽、高分别是8cm,8cm,12cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短行程是多少?(课本P15 T4)
B2
B1
解:由勾股定理得:
AB12=82+202=464
AB22=162+122=400
∵AB12>AB22
∴AB2=20cm
∴蚂蚁要爬行的最短行程是20cm
1.如图,圆柱形玻璃杯,高为12cm,底面周长
为18cm,在杯内离杯底4cm的点C处有一滴蜂
蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm
与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的
最短距离为 cm.
15
选做题
2.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC= BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是_________
3、有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是_________
正本作业:P19 T12.
5cm
3米
1.如图,圆柱形玻璃杯,高为12cm,底面周长18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
·
A
·
C
A1
15
9
4
4
4
选做题答案
2.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC= BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是多少?
∵圆柱的底面周长为6cm,
∴AC1=3cm,
∵PC1= BC1,
∴PC1= ×6=4cm,
在Rt△ACP中,
AP2=AC12+CP2=32+42=52, ∴AP=5
因此最短距离是5cm
C1
解:侧面展开图如图所示,
3、有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
解:图形可简化为左下图,设伸入油桶中的长度为x米,即AB=x米,而AC=2米,BC=1.5米,有
故,铁棒最长是2.5+0.5=3(米)
因此:这根铁棒的最长3米,最短2米.
故,最短是1.5+0.5=2(米)
当铁棒最短时:
A
C
B
最短是多少米?
解:长方体侧面展开图一共有三种情况,如上图,其距离分别是:
正本作业:P19 T12.
AB12=AD2+B1D2=202+(10+5)2=625=252
AB22=AE2+B2E2=102+(20+5)2=725
AB32=AC2+B3C2=(10+20)2+52=925
∵AB32 > AB22 > AB12
所以蚂蚁需要爬行的最短路程是AB1,距离是25cm.
(1)
(2)
(3)
板 书 设 计:
1.3勾股定理的应用(1)
一、立体图形求最短路径问题的思路:
1. 立体图形展开成平面图形。
2.根据 “两点之间,线段最短”,构建直角三角形利用勾股定理求解。
二、正方体最短路径d计算方法
d2=a2+4a2=5a2
三、长方体最短路径d计算方法
d2=a2+(b+c)2
最大棱长
1.3.1 勾股定理的应用
第一章 勾股定理
课前提问:(2分钟)
1、什么是勾股定理?用字母怎么表示?
直角三角形两直角边的平方和等于斜边的平方。如果用a、b、c
分别表示直角三角形的两直角边和斜边,那么a2+b2=c2
2、勾股定理的逆定理是什么?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
3、什么是勾股数?有哪些常见的勾股数?
满足a2 +b2=c2的三个正整数,称为勾股数.常见的勾股数:3、4、5;6、8、10;5、12、13;8,15,17;
7,24,25;9,40,41…
学习目标(1分钟)
1、掌握立体图形中圆柱体和长方体的最短线路问题的解题思路;
2、熟练运用勾股定理及其逆定理解决实际问题。
自学指导1(1分钟)
仔细阅读课本P13 “做一做”之前的内容,思考并回答下列问题:
如图,有一个圆柱体,它的高等于12cm,底面上圆的周长等于18cm。在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱体侧面爬行到B点。
3、哪条路径最短?最短路程是多少?
1、从A点沿圆柱侧面到B点有多少条路径?
答:有无数多条。
●
A
A
B
C
●
●
B
C
●
2、如将其侧面展开,A点在矩形左下角,则B点在哪?
答:B在上边的中点处。
答:线段AB最短。最短路程是15cm.
自学(3分钟)
有一圆形油罐底面圆的周长为24m,高为6m,一只蚂蚁从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
A
B
解:如图所示:
AC = 6 – 1 = 5 m,
BC = 24 × = 12m,
由勾股定理得
AB2= AC2+ BC2=169,
∴AB=13m
B
A
C
2
1
自学检测1(5分钟)
因此蚂蚁爬行的最短路线长为13m
讨论、更正、点拨(2分钟)
蚂蚁怎样沿圆柱体侧面从A点爬行到B点最近?
A
B
A
B
A
B
A
B
(1)
(2)
(3)
(4)
方法点拨:圆柱体(或几何体)表面求最短路径
①展(将路径经过的侧面展开在同一平面上)
②找(在展开平面上找对应点)
③连(用线段将两对应点连接,最短路径为该线段)
④解(利用勾股定理求③ 中线段长即得解)
如图正方体棱长为a,如图一只蚂蚁从A点经正方体表面爬行到G点。
1、蚂蚁经过哪些正方体表面能从A点爬行到G点?
A
B
C
D
E
F
G
H
2、有最短路径吗?请通过计算说明?
自学指导2(1分钟)
学生自学、教师巡视(3分钟)
1、解:蚂蚁可从侧面
共6种情况从A点爬行到G点。
前
上
右
下
后
右
左
上
后
如图正方体棱长为a,如图一只蚂蚁从A点经正方体表面爬行到G点。
1、蚂蚁经过哪些正方体表面能从A点爬行到G点?
2、有最短路径吗?请通过计算说明?
自学指导2(1分钟)
学生自学、教师巡视(3分钟)
a
a
a
前
右
A
B
C
D
E
F
G
H
2、解: ①前侧面+右侧面(或左侧面+后侧面)
点拨(2分钟)正方体爬行路径(分三种情况)
正方体爬行路径三种情况都相等
d2=a2+4a2=5a2
A
B
F
E
H
G
前(后)
上(下)
(3)
d
a
a
a
a
所以,有最短路径,长的平方为5a2
前(后)
右(左)
B
C
A
E
F
G
(1)
d
a
a
a
D
A
E
H
G
F
左(右)
(2)
d
a
a
a
上(下)
A
B
C
D
E
F
G
H
●
●
解:
如把正方体变成如下图的长方体,长方体底面长为2,宽为1,高为4,蚂蚁从A点沿长方体表面爬到E点有多少种爬行可能?哪种爬行路径的距离最短?是多少?
自学检测2(4分钟)
解:长方体侧面展开图一共有三种情况,如上图,其距离分别是:
第一种:
第二种:
第三种:
D
A
G
H
F
E1
2
4
1
左(右)
上(下)
(1)
B
A
G
F
H
E2
2
4
1
前(后)
上(下)
(2)
A
B
C
F
G
E3
4
1
2
前
(后)
右(左)
(3)
AE12=22+52=29
AE22=12+62=37
AE32=32+42=25
∵AE22 > AE12>AE32
∴最短路径是AE3,距离是5
点拨:(4分钟)
长方体的最短路径d的计算方法为 d =a +(b+c) ,其中a为最大棱长。
小结:(2分钟)
一、立体图形求最短路径问题的思路:
二、正方体最短路径d计算方法
d2=a2+4a2=5a2
三、长方体最短路径d计算方法
d2=a2+(b+c)2
最大棱长
方法点拨:几何体表面求最短路径
①展(将路径经过的侧面展开在同一平面上)
②找(在展开平面上找对应点)
③连(用线段将两对应点连接,最短路径为该线段)
④解(利用勾股定理求③ 中线段长即得解)
当堂训练(14分钟)
2、如右下图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A
1.如图,一只蚂蚁从A点沿圆柱侧面爬到顶面相对的B点处,如果圆柱的高为8 cm,圆柱的半径为 cm,那么最短路径AB长( ).
D
A.8 B.6 C.平方后为208的数 D.10
12≤a≤13 B.12≤a≤15
C. 5≤a≤12 D. 5≤a≤13
A
B
O
3.如图,台阶A处的蚂蚁要爬到B处搬运食物,最近距离是 。
分析:
25
4、一个无盖的长方体形盒子的长、宽、高分别是8cm,8cm,12cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,你能帮蚂蚁设计一条最短的线路吗?蚂蚁要爬行的最短行程是多少?(课本P15 T4)
B2
B1
解:由勾股定理得:
AB12=82+202=464
AB22=162+122=400
∵AB12>AB22
∴AB2=20cm
∴蚂蚁要爬行的最短行程是20cm
1.如图,圆柱形玻璃杯,高为12cm,底面周长
为18cm,在杯内离杯底4cm的点C处有一滴蜂
蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm
与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的
最短距离为 cm.
15
选做题
2.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC= BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是_________
3、有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是_________
正本作业:P19 T12.
5cm
3米
1.如图,圆柱形玻璃杯,高为12cm,底面周长18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
·
A
·
C
A1
15
9
4
4
4
选做题答案
2.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC= BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是多少?
∵圆柱的底面周长为6cm,
∴AC1=3cm,
∵PC1= BC1,
∴PC1= ×6=4cm,
在Rt△ACP中,
AP2=AC12+CP2=32+42=52, ∴AP=5
因此最短距离是5cm
C1
解:侧面展开图如图所示,
3、有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
解:图形可简化为左下图,设伸入油桶中的长度为x米,即AB=x米,而AC=2米,BC=1.5米,有
故,铁棒最长是2.5+0.5=3(米)
因此:这根铁棒的最长3米,最短2米.
故,最短是1.5+0.5=2(米)
当铁棒最短时:
A
C
B
最短是多少米?
解:长方体侧面展开图一共有三种情况,如上图,其距离分别是:
正本作业:P19 T12.
AB12=AD2+B1D2=202+(10+5)2=625=252
AB22=AE2+B2E2=102+(20+5)2=725
AB32=AC2+B3C2=(10+20)2+52=925
∵AB32 > AB22 > AB12
所以蚂蚁需要爬行的最短路程是AB1,距离是25cm.
(1)
(2)
(3)
板 书 设 计:
1.3勾股定理的应用(1)
一、立体图形求最短路径问题的思路:
1. 立体图形展开成平面图形。
2.根据 “两点之间,线段最短”,构建直角三角形利用勾股定理求解。
二、正方体最短路径d计算方法
d2=a2+4a2=5a2
三、长方体最短路径d计算方法
d2=a2+(b+c)2
最大棱长
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
