5.1.1相交线课件
图片预览






文档简介
课件25张PPT。温故知新1.直线、射线、线段的表示方法
2.直线的性质、线段的性质
3.线段中点的定义及几何语言
4.角的表示方法
5.角平分线的定义及几何语言
6.余角和补角的定义、性质
---5.1.1 相交线5.1 相交线两直线相交 我们已经知道,两条直线相交,只有一个交点。
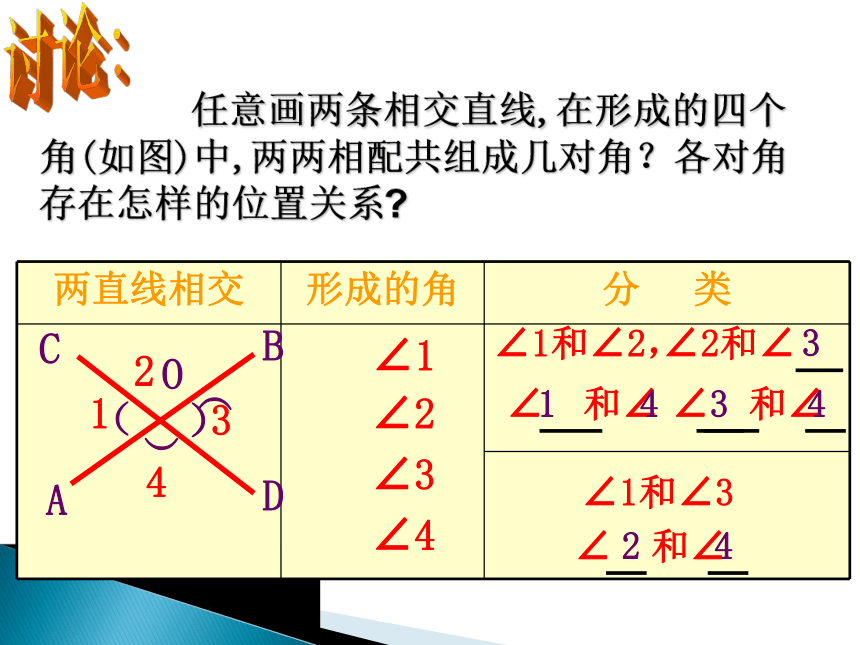
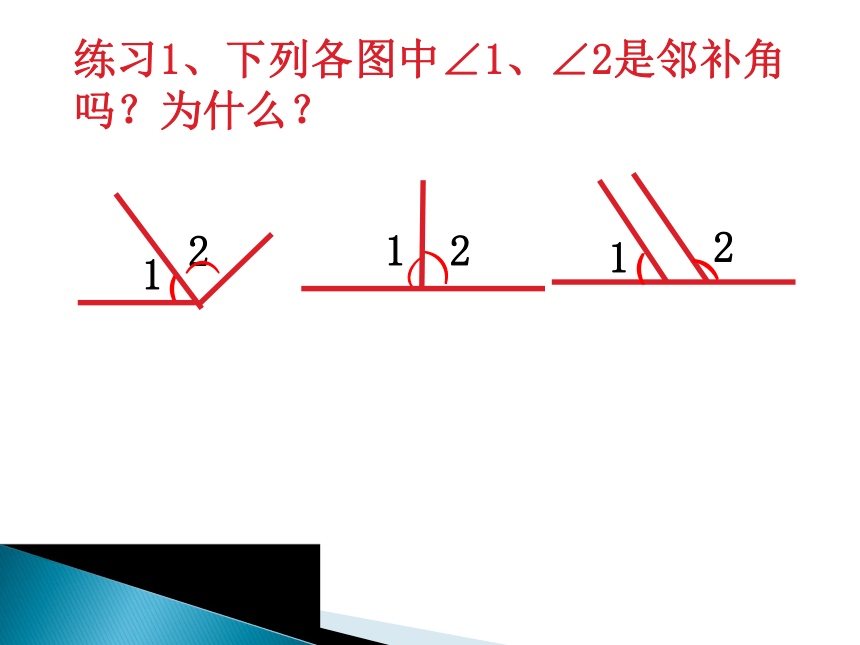
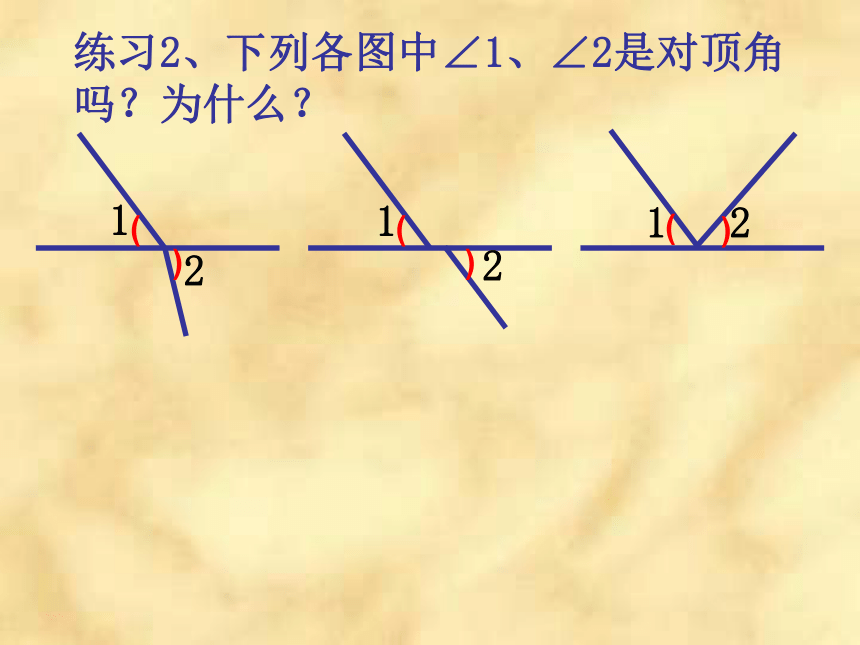
如上图,直线AB与直线CD相交,交点为O,可以说成“直线AB、CD相交于点O”。CD ABO(2)看看这几个角有什么位置关系?请用自己的话分别说一说。(1)这两条相交直线形成的小于平角的角有几个?探究请任意画两条相交直线,并回答下列问题: 任意画两条相交直线,在形成的四个角(如图)中,两两相配共组成几对角?各对角存在怎样的位置关系?讨论:O)(2∠3∠1∠2∠4∠1和∠2,414343∠1和∠32OABCD)(1342)( 有关概念: 如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。邻补角:练习1、下列各图中∠1、∠2是邻补角吗?为什么?21(((OABCD)(1342)(对顶角: 如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。有关概念: 1练习2、下列各图中∠1、∠2是对顶角吗?为什么?21212)((())判断下列图形中, ∠1, ∠2 是否是对顶角?判断下列各图中的∠1和∠2是不是对顶角。
请判断:下列的∠1与∠2是否是对顶角?(1)(2)(3)(4)(5)(6)(7)(若∠1= ∠2)(若∠1= ∠2)(若∠1= ∠2)练一练火眼金睛写出下列各图中的邻补角、对顶角.
ABCDEFGMIJKLOPN探究2猜想,并用量角器验证:
邻补角的关系
对顶角的关系 对顶角相等. 对顶角的性质:OABCD)(1342 ) ( 为什么?已知:如图,直线AB与CD相交于点O.
求证:∠1=∠3、 ∠2=∠4证明:∵直线AB与CD相交于点O,∴∠1+∠2=180°,∠2+∠3=180°∴∠1=∠3同理可得:∠2=∠4(同角的补角相等)ab)(1342)(例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。【例2】如图,AB、BC、AC都是直线,且∠1=∠2,那么∠3=∠1吗?为什么?例3:如图,已知直线AD与BE相交于点O,解:由对顶角相等,得
∠BOD=∠AOC=80°
∴∠2=∠ BOD -∠1 = 80°-1、一个角的对顶角有 个,邻补角最多有
个,而补角则可以有 个。3、如图,直线AB、CD相交于O,∠AOC=80°∠1=30°;求∠2的度数.ACBDE1一两无数练一练:2、右图中∠AOC的对顶角是 ,
邻补角是 .∠BOD∠AOD和∠BOC2))O30°= 50 °4.已知:如图, ∠ 1=70度,OE平分 ∠ AOC,
求 ∠ EOC和 ∠ BOC的度数。5.如图1,直线AB、CD交EF于点G、H∠2=∠3,∠1=70°。
求∠4的度数。
(1)两条直线相交,有 ___ 个交点,有____ 对对顶角,有____对邻补角 。
(2)三条直线相交,最少有___个交点,最多有____个交点,有____对对顶角,有____对邻补角。
(3)四条直线相交,最少有___个交点,最多有____个交点,有____对对顶角,有____对邻补角。
······
(4)n条直线相交,最少有____个交点,最多有______个交点,______对对顶角,______ _邻补角。活动与探究124136121612241n(n-1)2n(n-1)?n(n-1)归纳对顶
角相
等
邻补
角互
补 ②有公共顶点;③没有公共边①两条直线相交形成的角; ①两条直线相交而成;②有公共顶点;③有一条公共边①都是两条直线相交而成的角;③都是成对出现的 ②都有一个公共顶点;②两直线相交时,
对顶角只有两对
邻补角有四对 ①有无公共边课堂小结1.直线相交及交点概念.
2.对顶角定义及判断方法.
对顶角判断条件: (1) 两条直线相交. (2)有公共顶点. (3)无公共边.
3.对顶角的性质:对顶角相等.
4.利用学习过的有关事实解决实际问题,体会数学在生活中的应用.课本P8 第2、8题作业
2.直线的性质、线段的性质
3.线段中点的定义及几何语言
4.角的表示方法
5.角平分线的定义及几何语言
6.余角和补角的定义、性质
---5.1.1 相交线5.1 相交线两直线相交 我们已经知道,两条直线相交,只有一个交点。
如上图,直线AB与直线CD相交,交点为O,可以说成“直线AB、CD相交于点O”。CD ABO(2)看看这几个角有什么位置关系?请用自己的话分别说一说。(1)这两条相交直线形成的小于平角的角有几个?探究请任意画两条相交直线,并回答下列问题: 任意画两条相交直线,在形成的四个角(如图)中,两两相配共组成几对角?各对角存在怎样的位置关系?讨论:O)(2∠3∠1∠2∠4∠1和∠2,414343∠1和∠32OABCD)(1342)( 有关概念: 如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。邻补角:练习1、下列各图中∠1、∠2是邻补角吗?为什么?21(((OABCD)(1342)(对顶角: 如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。有关概念: 1练习2、下列各图中∠1、∠2是对顶角吗?为什么?21212)((())判断下列图形中, ∠1, ∠2 是否是对顶角?判断下列各图中的∠1和∠2是不是对顶角。
请判断:下列的∠1与∠2是否是对顶角?(1)(2)(3)(4)(5)(6)(7)(若∠1= ∠2)(若∠1= ∠2)(若∠1= ∠2)练一练火眼金睛写出下列各图中的邻补角、对顶角.
ABCDEFGMIJKLOPN探究2猜想,并用量角器验证:
邻补角的关系
对顶角的关系 对顶角相等. 对顶角的性质:OABCD)(1342 ) ( 为什么?已知:如图,直线AB与CD相交于点O.
求证:∠1=∠3、 ∠2=∠4证明:∵直线AB与CD相交于点O,∴∠1+∠2=180°,∠2+∠3=180°∴∠1=∠3同理可得:∠2=∠4(同角的补角相等)ab)(1342)(例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。【例2】如图,AB、BC、AC都是直线,且∠1=∠2,那么∠3=∠1吗?为什么?例3:如图,已知直线AD与BE相交于点O,解:由对顶角相等,得
∠BOD=∠AOC=80°
∴∠2=∠ BOD -∠1 = 80°-1、一个角的对顶角有 个,邻补角最多有
个,而补角则可以有 个。3、如图,直线AB、CD相交于O,∠AOC=80°∠1=30°;求∠2的度数.ACBDE1一两无数练一练:2、右图中∠AOC的对顶角是 ,
邻补角是 .∠BOD∠AOD和∠BOC2))O30°= 50 °4.已知:如图, ∠ 1=70度,OE平分 ∠ AOC,
求 ∠ EOC和 ∠ BOC的度数。5.如图1,直线AB、CD交EF于点G、H∠2=∠3,∠1=70°。
求∠4的度数。
(1)两条直线相交,有 ___ 个交点,有____ 对对顶角,有____对邻补角 。
(2)三条直线相交,最少有___个交点,最多有____个交点,有____对对顶角,有____对邻补角。
(3)四条直线相交,最少有___个交点,最多有____个交点,有____对对顶角,有____对邻补角。
······
(4)n条直线相交,最少有____个交点,最多有______个交点,______对对顶角,______ _邻补角。活动与探究124136121612241n(n-1)2n(n-1)?n(n-1)归纳对顶
角相
等
邻补
角互
补 ②有公共顶点;③没有公共边①两条直线相交形成的角; ①两条直线相交而成;②有公共顶点;③有一条公共边①都是两条直线相交而成的角;③都是成对出现的 ②都有一个公共顶点;②两直线相交时,
对顶角只有两对
邻补角有四对 ①有无公共边课堂小结1.直线相交及交点概念.
2.对顶角定义及判断方法.
对顶角判断条件: (1) 两条直线相交. (2)有公共顶点. (3)无公共边.
3.对顶角的性质:对顶角相等.
4.利用学习过的有关事实解决实际问题,体会数学在生活中的应用.课本P8 第2、8题作业
