函数的应用
图片预览





文档简介
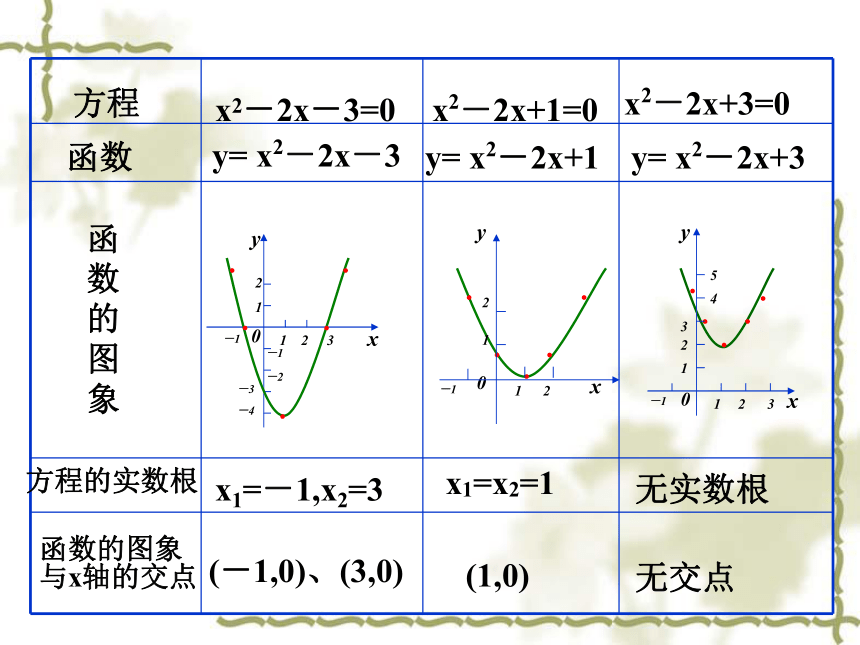
课件17张PPT。3.1.1 方程的根与函数的零点方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根
函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3方程ax2 +bx+c=0
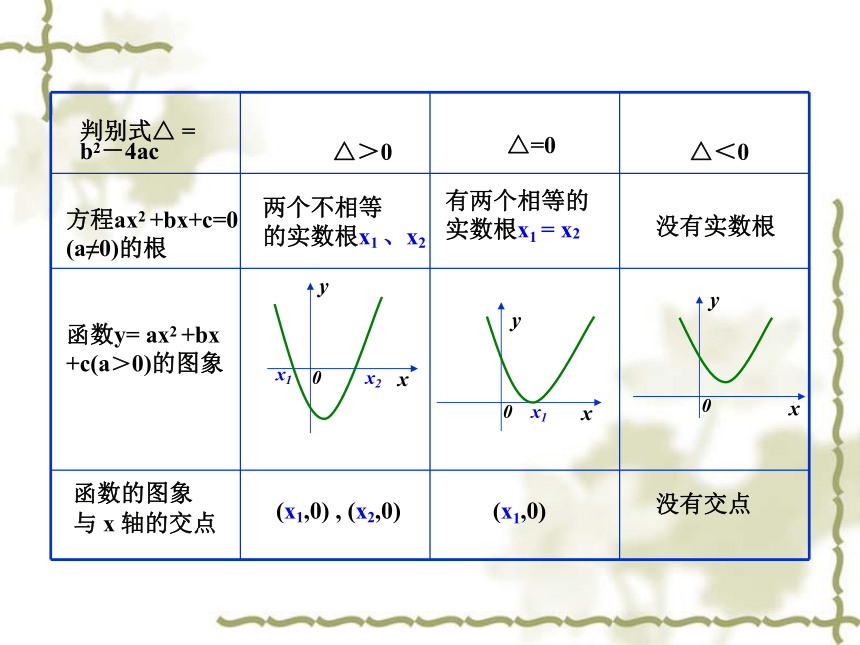
(a≠0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2 对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点。函数零点的定义:方程f(x)=0有实数根c零点是点吗?2、求下列函数的零点:
练习求函数零点方法:①方程法②图象法
数学思想:转化思想和数形结合思想1、如果二次函数y=x2+2x+(m+3)有两个不同的零点,则m的取值范围是( )
A、m> – 2 B、m< – 2 C、m>2 D、m<2B函数的图象不易画出,又不能求相应方程的根,怎样判断函数是否有零点?想一想?012345-1-212345-1-2-3-4xy探究零点存在性的探索 结论思考1:零点唯一吗?思考2:是否所有函数都有零点?思考3:若只给f(a)f(b)<0,能否保证在区间(a,b)内有零点?若函数在区间(a,b)内有零点,是否一定有f(a)f(b)<0?
函数在区间(a,b)上为单调函数,若f(a) ·f(b)<0,则函数在(a,b)上有且只有一个零点.1、已知函数f(x)的图象是连续不断的,有如下的 x , f(x) 对应值表:练一练那么函数在区间[1,6]上的零点至少有( )个
A 5 B 4 C 3 D 2C2、求证:方程 在(1,2)内必有一个实数根。
等价f(x)=0有实根y=f(x)与x轴有交点y=f(x)有零点等价 如果函数y=f(x)在[a, b]上的图象是连续不断的一
条曲线,并且f(a)·f(b)<0,那么,函数y=f(x)在区间
(a, b)内有零点,即存在c∈(a, b),使得f( c )=0,这个c 就
是方程f(x)=0的根。
小结课后思考1、函数零点判断方法有哪几种?2、如何求函数f(x)=lnx+2x-6的零点个数及零点所在的大致区间?【作业】
88页练习T1
92页习题3.1 T2
导学谢谢指导! 情景导入根据新华社报道:昨晚足球比赛跌宕起伏,球迷经历了大喜到大悲,再到大喜的过程(领先则喜,落后则悲).
请问:整场比赛出现几次“比分相同”的时段?
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根
函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3方程ax2 +bx+c=0
(a≠0)的根函数y= ax2 +bx
+c(a>0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2 对于函数y=f(x),我们把使f(x)=0的实数x
叫做函数y=f(x)的零点。函数零点的定义:方程f(x)=0有实数根c零点是点吗?2、求下列函数的零点:
练习求函数零点方法:①方程法②图象法
数学思想:转化思想和数形结合思想1、如果二次函数y=x2+2x+(m+3)有两个不同的零点,则m的取值范围是( )
A、m> – 2 B、m< – 2 C、m>2 D、m<2B函数的图象不易画出,又不能求相应方程的根,怎样判断函数是否有零点?想一想?012345-1-212345-1-2-3-4xy探究零点存在性的探索 结论思考1:零点唯一吗?思考2:是否所有函数都有零点?思考3:若只给f(a)f(b)<0,能否保证在区间(a,b)内有零点?若函数在区间(a,b)内有零点,是否一定有f(a)f(b)<0?
函数在区间(a,b)上为单调函数,若f(a) ·f(b)<0,则函数在(a,b)上有且只有一个零点.1、已知函数f(x)的图象是连续不断的,有如下的 x , f(x) 对应值表:练一练那么函数在区间[1,6]上的零点至少有( )个
A 5 B 4 C 3 D 2C2、求证:方程 在(1,2)内必有一个实数根。
等价f(x)=0有实根y=f(x)与x轴有交点y=f(x)有零点等价 如果函数y=f(x)在[a, b]上的图象是连续不断的一
条曲线,并且f(a)·f(b)<0,那么,函数y=f(x)在区间
(a, b)内有零点,即存在c∈(a, b),使得f( c )=0,这个c 就
是方程f(x)=0的根。
小结课后思考1、函数零点判断方法有哪几种?2、如何求函数f(x)=lnx+2x-6的零点个数及零点所在的大致区间?【作业】
88页练习T1
92页习题3.1 T2
导学谢谢指导! 情景导入根据新华社报道:昨晚足球比赛跌宕起伏,球迷经历了大喜到大悲,再到大喜的过程(领先则喜,落后则悲).
请问:整场比赛出现几次“比分相同”的时段?
