百分数(一)解决问题精选题提升篇(含答案)数学六年级上册人教版
文档属性
| 名称 | 百分数(一)解决问题精选题提升篇(含答案)数学六年级上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 20:57:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
百分数(一)解决问题精选题(提升篇)数学六年级上册人教版
1.为了备战运动会,国家射击队进行一次赛前选拔赛.小丽和李明各自的命中率是多少?
2.学校想把一块长方形空地(如下图)修整出一块最大的正方形地来种植草坪,你给算一算,正方形草坪的面积比原长方形空地的面积大约小百分之几?(百分号前面的数保留一位小数)
3.11月初鸡蛋价格比10月初上涨了15%,12月初又比11月初回落了10%。12月初鸡蛋价格与10月初比是涨了还是跌了?涨跌幅度是多少?
4.某工程队修一段公路,第一周修了这段公路的25%,第二周修了这段公路的。两周正好修了135千米,这段公路一共有多少千米?
5.中国人民银行决定于2021年8月30日发行中国首次火星探测任务成功的纪念币一套,其中面额为2000元的圆形金质纪念币质量为150克,面额为100元的圆形金质纪念币质量为8克,面额为100元的圆形金质纪念币质量是面额为2000元的圆形金质纪念币质量的百分之几?(百分号前保留一位小数)
6.大华服装厂去年生产童装3284套,今年前4个月的产量等于去年全年产量的75%,照这样计算,今年可生产童装多少套?
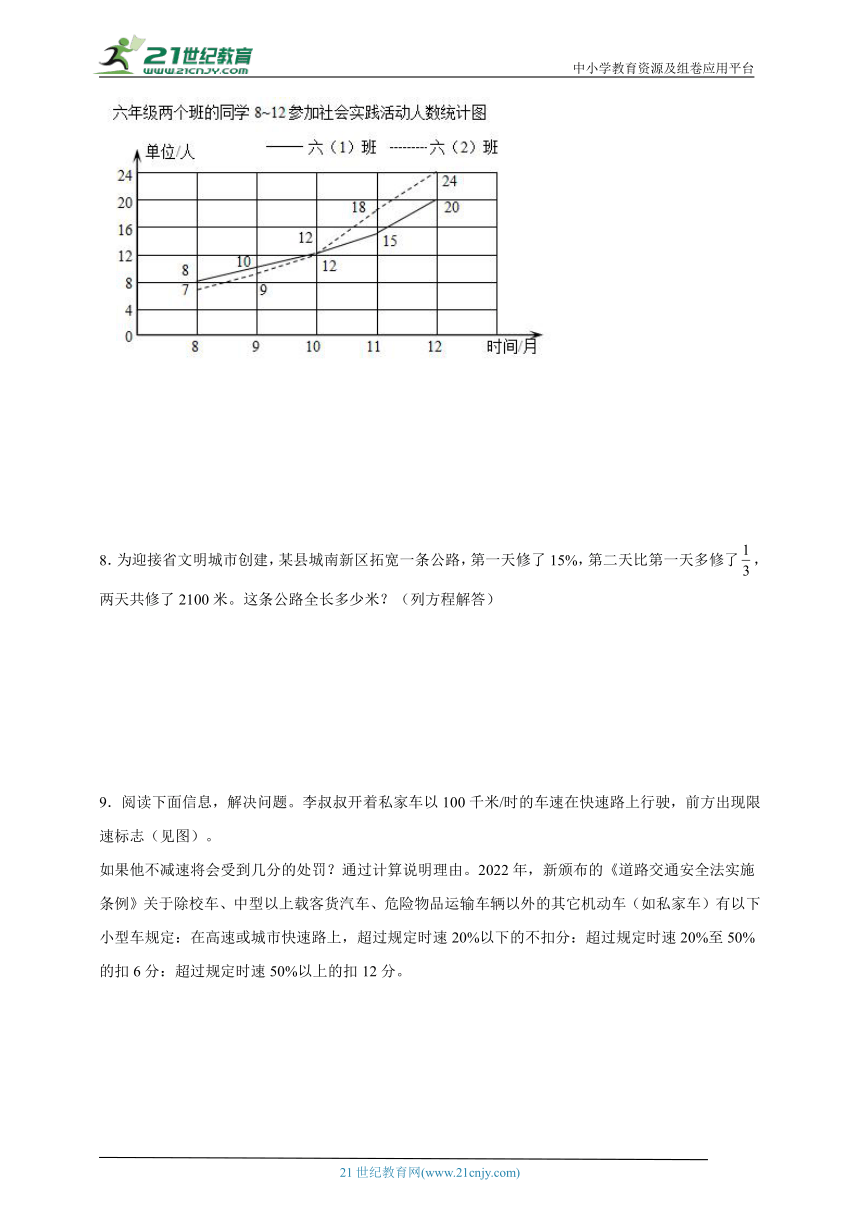
7.光明小学六年级两个班同学2011年8~12月份参加社会实践活动人数统计如下,请你看图回答下面的问题。
(1)六(1)班8~12月平均每个月参加社会实践活动的有多少人?
(2)六(2)班12月参加社会实践活动的人数比六(1)班多百分之几?
(3)根据统计图,简单分析六年级学生参加社会实践活动人数变化的发展趋势。
8.为迎接省文明城市创建,某县城南新区拓宽一条公路,第一天修了15%,第二天比第一天多修了,两天共修了2100米。这条公路全长多少米?(列方程解答)
9.阅读下面信息,解决问题。李叔叔开着私家车以100千米/时的车速在快速路上行驶,前方出现限速标志(见图)。
如果他不减速将会受到几分的处罚?通过计算说明理由。2022年,新颁布的《道路交通安全法实施条例》关于除校车、中型以上载客货汽车、危险物品运输车辆以外的其它机动车(如私家车)有以下小型车规定:在高速或城市快速路上,超过规定时速20%以下的不扣分:超过规定时速20%至50%的扣6分:超过规定时速50%以上的扣12分。
10.为实现村村通公路计划,某政府决定从甲村到乙村修一条乡村公路。第一个月修了全长的20%,第二个月修了全长的,还剩下810米没修,这条乡村公路有多长?
11.某网店老板将500元进价的一件羽绒服先提价20%销售,临近春节,店铺做活动又降价10%出售,现在一件羽绒服赚多少元?
12.王爷爷参加了农村合作医疗保险,条款规定:参保者住院医疗费报销设起付线,县二级医院的起付线为400元。住院费不超过6000元,在起付线以上的部分按65%报销;超过6000元的在起付线以上的部分按80%报销。今年5月份王爷爷意外受伤,在县二级医院住院30天,医疗费用共计7500元,按条款规定,王爷爷只需自己付多少元?
13.昊明第一天看了一本书的20%,第二天看了15页,这时已看的页数与未看的页数之比为2∶3,这本书一共有多少页?
14.华为已经彻底解决了5G难题,国内芯片厂商华为已经突破了5G射频芯片技术的难题,根据6月6日网上消息显示,2023年华为的手机出货量为4000万台,原计划出货量是3700万台,原计划手机出货量比实际手机出货量少百分之几?
15.如图是一块黑白格子布.白色大正方形的边长是14厘米,白色小正方形的边长是6 厘米.问:这块布中白色的面积占总面积的百分之几?
16.一筐苹果,第一天吃了10个,第二天吃的苹果是第一天的,这筐苹果还剩70%,这筐苹果原来有多少个?
17.2019年年底某市机动车保有量630万辆。每辆机动车平均每千米的二氧化碳排放量约为,按每辆机动车每年行驶计算,回答下列问题。
(1)该市2019年年底保有的机动车在2020年排放二氧化碳约多少万吨?
(2)在有效措施的限制下,预计该市2021年机动车的二氧化碳排放量比2020年降低一成到一成五,该市2021年机动车的二氧化碳排放量预计不超过多少万吨?
18.甲、乙两辆汽车同时从A地开往B地,先到B地的立即返回,两车在离B地24千米处相遇。已知甲车速度是每小时80千米,乙车速度比甲车慢20%。A、B两地间的路程是多少千米?(温馨提醒:画画线段图,能帮助你更直观地理解题意哦!)
19.实验小学对1500名学生进行了阅读调查,调查的结果如下:
网络阅读占8%;
电子器阅读比网络阅读少25%;
图书阅读比网络阅读多45%.
(1)通过网络阅读的学生有多少人?
(2)通过电子器阅读的学生有多少人?
(3)通过图书阅读的学生有多少人?
20.一辆汽车从A城开往B城,上午行了全程的40%,下午行了210千米,这时已行路程和剩下路程的比是3∶1,求A、B两城之间相距多少千米?
21.如图,两个长方形重叠部分的面积相当于小长方形面积的,相当于大长方形面积的20%。
(1)如果小长方形的面积是40平方厘米,那么大长方形的面积是多少平方厘米?
(2)如果重叠部分的面积是25平方厘米,那么大长方形和小长方形的面积各是多少平方厘米?
参考答案:
1.小丽93.75%;李明93.3%
【详解】75÷80×100%=93.75%
56÷60×100%≈93.3%
2.33.3%
【分析】长方形内最大的正方形的边长等于这个长方形的宽12米,据此利用长方形和正方形的面积公式分别计算出它们的面积即可解答问题.
【详解】12×12=144(平方米),
12×18=216(平方米),
(216﹣144)÷216,
=72÷216,
≈33.3%.
答:正方形草坪的面积比原长方形空地的面积大约小33.3%.
3.涨了;3.5%
【分析】假设10月初鸡蛋价格10元,11月初鸡蛋价格比10月初上涨了15%,11月初鸡蛋价格是10月初的(1+15%),10月初鸡蛋价格×11月初对应百分率=11月初鸡蛋价格;再将11月初鸡蛋价格看作单位“1”,12月初比11月初回落了10%,12月初鸡蛋价格是11月初的(1-10%),11月初鸡蛋价格×12月初对应百分率=12月初鸡蛋价格,比较即可确定涨了还是跌了,12月初与10月初鸡蛋价格的差÷10月初鸡蛋价格=涨百分之几。
【详解】假设10月初鸡蛋价格10元。
10×(1+15%)×(1-10%)
=10×1.15×0.9
=10.35(元)
10.35>10
(10.35-10)÷10
=0.35÷10
=3.5%
答:12月初鸡蛋价格与10月初比是涨了,涨了3.5%。
【点睛】关键是确定单位“1”,整体数量×部分对应百分率=部分数量,差÷较小数=增加百分之几。
4.300千米
【分析】将公路总长看成单位“1”,两周共修25%+,用两周修的实际长度÷对应分率或百分率即可。
【详解】135÷(25%+)
=135÷0.45
=300(千米)
答:这段公路一共有300千米。
【点睛】关键是确定单位“1”,部分数量÷对应分率或百分率=整体数量。
5.5.3%
【分析】用100元的圆形纪念币除以2000元的圆形纪念币的质量再乘100%计算即可。
【详解】8÷150×100%
≈0.053×100%
=5.3%
答:面额为100元的圆形金质纪念币质量是面额为2000元的圆形金质纪念币质量的5.3%。
【点睛】本题关键在于对一个数是另一个数的百分之几的求法,这里用除法计算。
6.7389套
【分析】将去年生产数量看作单位“1”,去年生产数量×今年前4个月的产量对应百分率=今年前4个月的产量;一年有12个月,4个月占全年的,再将今年生产数量看作单位“1”,今年前4个月的产量÷对应分率=今年生产数量,据此列式解答。
【详解】3284×75%÷
=3284×0.75÷
=2463×
=7389(套)
答:今年可生产童装7389套。
【点睛】关键是确定单位“1”,整体数量×部分对应百分率=部分数量,部分数量÷对应分率=整体数量。
7.(1)13人;
(2)20%;
(3)六年级学生参加社会实践活动人数变化呈上升趋势
【分析】(1)把六(1)班8~12月参加社会实践活动的总人数除以5即可;
(2)六(2)班12月参加社会实践活动的人数比六(1)班多百分之几,用多的人数除以六(1)班12月参加社会实践活动的人数即可;
(3)根据折线统计图可知,六年级学生参加社会实践活动人数每个月的数量都在增加,即人数变化呈上升趋势。
【详解】(1)(8+10+12+15+20)÷5
=65÷5
=13(人)
答:六(1)班8~12月平均每个月参加社会实践活动的有13人。
(2)(24﹣20)÷20
=4÷20
=20%
答:六(2)班12月参加社会实践活动的人数比六(1)班多百分之二十。
(3)根据折线统计图可知,六年级学生参加社会实践活动人数变化呈上升趋势。
【点睛】此题主要考查的是如何从折线统计图中获取信息,然后再根据信息进行计算、分析、解答即可。
8.6000米
【分析】把这条公路长看作单位“1”,设这条公路全长x米,则第一天修了15%x米,第二天修了15%x×+15%x米,根据两天共修了2100米列方程解答。
【详解】解:设这条公路全长x米,根据题意得:
15%x+15%x×+15%x=2100
x+x+x=2100
x=2100
x=2100÷
x=6000
答:这条公路全长6000米。
【点睛】此题考查的是列方程解决问题,解答此题关键是求出第二天修的长度。
9.6分;理由见详解
【分析】先根据求一个数比另一个数多百分之几,用相差数除以另一个数再乘100%,则用李叔叔实际的速度减去规定的时速,然后用它们的差除以规定的时速再乘100%,最后观察结果在哪个扣分范围即可。
【详解】理由如下:
(100-80)÷80×100%
=20÷80×100%
=25%
20%<25%<50%
答:李叔叔将被扣6分。
【点睛】本题考查了百分数的应用,明确求一个数比另一个数多百分之几,用除法计算。
10.1200米
【分析】把公路总长看作单位“1” ,用剩下的810米除以对应的分率是1-20%-即可求出公路长。
【详解】810÷(1-20%-)
=810÷
=1200(米)
答:这条乡村公路有1200米。
【点睛】此题考查的是分数除法的应用,找准单位“1”,明确求单位“1”的量用除法是解题关键。
11.40元
【分析】把这件羽绒服的原价看作单位“1”,先提价20%,提价后的价格是原价的(1+20%),单位“1”已知,用乘法求出提价后的价格;
又降价10%出售,再把提价后的价格看作单位“1”,降价后的价格是提价后价格的(1-10%),单位“1”已知,用乘法求出现价;
最后用现价减去原价,就是现在一件羽绒服赚的钱数。
【详解】现价:
500×(1+20%)×(1-10%)
=500×1.2×0.9
=600×0.9
=540(元)
赚了:540-500=40(元)
答:现在一件羽绒服赚40元。
【点睛】本题考查百分数的应用,区分两个单位“1”的不同,明确求比一个数多或少百分之几的数是多少,用乘法计算。
12.1820元
【分析】医疗费用共计7500元,已经超过6000元,在起付线以上的部分是(7500-400)元,按80%报销,则自己要付20%,即要交付(7500-400)×(1-80%)元,再加上起付线的钱数,最终求出王爷爷所需付的钱数。
【详解】(7500-400)×(1-80%)+400
=7100×0.2+400
=1420+400
=1820(元)
答:王爷爷只需自己付1820元。
【点睛】此题主要是找到关键节点6000元,按不同的标准报销,掌握求一个数的百分之几是多少的计算方法。
13.75页
【详解】解:设这本书一共有x页.
20%x+15=x
x =75
答:这本书一共有75页.
14.7.5%
【分析】根据求一个数比另一个数多(少)百分之几,用相差数除以另一个数再乘100%,则用(4000-3700)÷4000×100%即可求出原计划手机出货量比实际手机出货量少百分之几。
【详解】(4000-3700)÷4000×100%
=300÷4000×100%
=7.5%
答:原计划手机出货量比实际手机出货量少7.5%。
【点睛】本题主要考查了百分数的应用,明确求一个数比另一个数多(少)百分之几,用除法计算。
15.格子布中白色部分的面积是总面积的58%
【详解】试题分析:如图一共有3×3=9个格子,所以可得每个格子布的面积是图面积的9倍,格子布白色部分的面积也是图上白色面积的9倍,下图中白色部分所占面积的百分比=0.58=58%,据此即可解答.
解:=0.58=58%,
答:格子布中白色部分的面积是总面积的58%.
点评:解答此题的关键是明确每个格子中白色部分占格子的面积的百分比,就是这块布中白色的面积占总面积的百分之几.
16.60个
【分析】求一个数的几分之几是多少,用乘法,先用10乘,求出第二天吃的个数;把这筐苹果的总个数看作单位“1”,用1减去还剩下的70%,即两天吃了(1-70%),对应着两天吃了的个数,根据百分数除法的意义,用两天吃的总个数除以(1-70%),即可求出这筐苹果原来有多少个。
【详解】(10+10×)÷(1-70%)
=(10+8)÷30%
=18÷0.3
=60(个)
答:这筐苹果原来有60个。
【点睛】求一个数的几分之几是多少,用乘法计算;已知一个数的百分之几是多少,求这个数,用除法计算。
17.(1)1008万吨
(2)907.2万吨
【分析】(1)要求630万辆机动车全年的二氧化碳排放总量,需先求1辆机动车全年二氧化碳的排放量,列式为,为计算方便,将换算为,再进一步求出630万辆机动车全年的二氧化碳排放总量。
(2)降低一成到一成五,表示的含义就是降低10%到15%,也就是最少降低10%,由此可知该市2021年机动车的二氧化碳排放量预计不超过(万吨)。
【详解】(1)
(万吨)
答:该市2019年年底保有的机动车在2020年排放二氧化碳约1008万吨。
(2)
(万吨)
答:该市2021年机动车的二氧化碳排放量预计不超过907.2万吨。
【点睛】百分数运算的实际应用,需要我们熟悉百分数的意义及其计算方法;此外,从“克”到“吨”的转化,再到万吨,其中的计算稍显复杂,要细心一些;第二问求的是不超过多少万吨,因此不必将降低一成五的效果也计算出来,只要计算出降低一成的就可以。
18.216千米
【分析】将甲车速度看作单位“1”,那么乙车速度是甲车的(1-20%),据此利用乘法求出乙车的速度,从而利用减法求出速度差。根据题意,两车相遇时,甲车的路程比乙车多了(24×2)千米,将路程差除以速度差,求出甲车的行驶时间。根据“速度×时间=路程”求出甲车路程,再减去甲多行的24千米,求出A、B两地的距离即可。
【详解】乙车速度:
80×(1-20%)
=80×80%
=64(千米/时)
甲车每小时比乙车多行:80-64=16(千米)
甲车行驶时间:24×2÷16=3(小时)
两地路程:
80×3-24
=240-24
=216(千米)
答:A、B两地间的路程是216千米。
【点睛】本题考查了含百分数的运算、行程问题中的相遇问题。求比一个数少百分之几的数是多少,用乘法;路程差÷速度差=时间。
19.(1)120人 (2)90人 (3)174人
【详解】(1)1500×8%=120(人)
(2)120×(1-25%)=90(人)
(3)120×(1+45%)=174(人)
20.600千米
【分析】由题意可知,下午行了210千米,这时已行路程和剩下路程的比是3∶1,即此时已行的路程占总路程的,即210千米占总路程的(-40%),再根据除法的意义,用除法计算即可。
【详解】210÷(-40%)
=210÷
=210×
=600(千米)
答:A、B两城之间相距600千米。
【点睛】本题考查分数除法,明确部分的量除以所对应的分率等于单位“1”的量是解题的关键。
21.(1)50平方厘米
(2)大:125平方厘米;小:100平方厘米
【分析】已知两个长方形重叠部分的面积相当于小长方形面积的,相当于大长方形面积的20%。
(1)又知小长方形的面积是40平方厘米,则可先求得重叠部分面积,把小长方形的面积看作单位“1”,根据求一个数的几分之几是多少,用乘法计算,列式为:40×=10(平方厘米);
因为重叠部分面积相当于大长方形的20%,把大长方形的面积看作单位“1”,根据已知一个数的百分之几是多少,求这个数用除法计算,列式为10÷20%,综合算式为:40×÷20%;
(2)如果重叠部分的面积是25平方厘米,把小长方形的面积看作单位“1”,根据已知一个数的几分之几是多少,求这个数用除法计算,可知:要求得小长方形的面积,列式为:25÷;
把大长方形的面积看作单位“1”,根据已知一个数的百分之几是多少,求这个数用除法计算,要求得大正方形的面积,列式为:25÷20%。
【详解】(1)40×÷20%
=10÷0.2
=50(平方厘米)
答:大长方形的面积是50平方厘米。
(2)25÷=25×4=100(平方厘米)
25÷20%=125(平方厘米)
答:大长方形的面积是125平方厘米;小长方形的面积是100平方厘米。
【点睛】主要考查了单位“1”未知在分数除法中、百分数除法中的应用,需要理解:量÷对应分率=单位“1”的量。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
百分数(一)解决问题精选题(提升篇)数学六年级上册人教版
1.为了备战运动会,国家射击队进行一次赛前选拔赛.小丽和李明各自的命中率是多少?
2.学校想把一块长方形空地(如下图)修整出一块最大的正方形地来种植草坪,你给算一算,正方形草坪的面积比原长方形空地的面积大约小百分之几?(百分号前面的数保留一位小数)
3.11月初鸡蛋价格比10月初上涨了15%,12月初又比11月初回落了10%。12月初鸡蛋价格与10月初比是涨了还是跌了?涨跌幅度是多少?
4.某工程队修一段公路,第一周修了这段公路的25%,第二周修了这段公路的。两周正好修了135千米,这段公路一共有多少千米?
5.中国人民银行决定于2021年8月30日发行中国首次火星探测任务成功的纪念币一套,其中面额为2000元的圆形金质纪念币质量为150克,面额为100元的圆形金质纪念币质量为8克,面额为100元的圆形金质纪念币质量是面额为2000元的圆形金质纪念币质量的百分之几?(百分号前保留一位小数)
6.大华服装厂去年生产童装3284套,今年前4个月的产量等于去年全年产量的75%,照这样计算,今年可生产童装多少套?
7.光明小学六年级两个班同学2011年8~12月份参加社会实践活动人数统计如下,请你看图回答下面的问题。
(1)六(1)班8~12月平均每个月参加社会实践活动的有多少人?
(2)六(2)班12月参加社会实践活动的人数比六(1)班多百分之几?
(3)根据统计图,简单分析六年级学生参加社会实践活动人数变化的发展趋势。
8.为迎接省文明城市创建,某县城南新区拓宽一条公路,第一天修了15%,第二天比第一天多修了,两天共修了2100米。这条公路全长多少米?(列方程解答)
9.阅读下面信息,解决问题。李叔叔开着私家车以100千米/时的车速在快速路上行驶,前方出现限速标志(见图)。
如果他不减速将会受到几分的处罚?通过计算说明理由。2022年,新颁布的《道路交通安全法实施条例》关于除校车、中型以上载客货汽车、危险物品运输车辆以外的其它机动车(如私家车)有以下小型车规定:在高速或城市快速路上,超过规定时速20%以下的不扣分:超过规定时速20%至50%的扣6分:超过规定时速50%以上的扣12分。
10.为实现村村通公路计划,某政府决定从甲村到乙村修一条乡村公路。第一个月修了全长的20%,第二个月修了全长的,还剩下810米没修,这条乡村公路有多长?
11.某网店老板将500元进价的一件羽绒服先提价20%销售,临近春节,店铺做活动又降价10%出售,现在一件羽绒服赚多少元?
12.王爷爷参加了农村合作医疗保险,条款规定:参保者住院医疗费报销设起付线,县二级医院的起付线为400元。住院费不超过6000元,在起付线以上的部分按65%报销;超过6000元的在起付线以上的部分按80%报销。今年5月份王爷爷意外受伤,在县二级医院住院30天,医疗费用共计7500元,按条款规定,王爷爷只需自己付多少元?
13.昊明第一天看了一本书的20%,第二天看了15页,这时已看的页数与未看的页数之比为2∶3,这本书一共有多少页?
14.华为已经彻底解决了5G难题,国内芯片厂商华为已经突破了5G射频芯片技术的难题,根据6月6日网上消息显示,2023年华为的手机出货量为4000万台,原计划出货量是3700万台,原计划手机出货量比实际手机出货量少百分之几?
15.如图是一块黑白格子布.白色大正方形的边长是14厘米,白色小正方形的边长是6 厘米.问:这块布中白色的面积占总面积的百分之几?
16.一筐苹果,第一天吃了10个,第二天吃的苹果是第一天的,这筐苹果还剩70%,这筐苹果原来有多少个?
17.2019年年底某市机动车保有量630万辆。每辆机动车平均每千米的二氧化碳排放量约为,按每辆机动车每年行驶计算,回答下列问题。
(1)该市2019年年底保有的机动车在2020年排放二氧化碳约多少万吨?
(2)在有效措施的限制下,预计该市2021年机动车的二氧化碳排放量比2020年降低一成到一成五,该市2021年机动车的二氧化碳排放量预计不超过多少万吨?
18.甲、乙两辆汽车同时从A地开往B地,先到B地的立即返回,两车在离B地24千米处相遇。已知甲车速度是每小时80千米,乙车速度比甲车慢20%。A、B两地间的路程是多少千米?(温馨提醒:画画线段图,能帮助你更直观地理解题意哦!)
19.实验小学对1500名学生进行了阅读调查,调查的结果如下:
网络阅读占8%;
电子器阅读比网络阅读少25%;
图书阅读比网络阅读多45%.
(1)通过网络阅读的学生有多少人?
(2)通过电子器阅读的学生有多少人?
(3)通过图书阅读的学生有多少人?
20.一辆汽车从A城开往B城,上午行了全程的40%,下午行了210千米,这时已行路程和剩下路程的比是3∶1,求A、B两城之间相距多少千米?
21.如图,两个长方形重叠部分的面积相当于小长方形面积的,相当于大长方形面积的20%。
(1)如果小长方形的面积是40平方厘米,那么大长方形的面积是多少平方厘米?
(2)如果重叠部分的面积是25平方厘米,那么大长方形和小长方形的面积各是多少平方厘米?
参考答案:
1.小丽93.75%;李明93.3%
【详解】75÷80×100%=93.75%
56÷60×100%≈93.3%
2.33.3%
【分析】长方形内最大的正方形的边长等于这个长方形的宽12米,据此利用长方形和正方形的面积公式分别计算出它们的面积即可解答问题.
【详解】12×12=144(平方米),
12×18=216(平方米),
(216﹣144)÷216,
=72÷216,
≈33.3%.
答:正方形草坪的面积比原长方形空地的面积大约小33.3%.
3.涨了;3.5%
【分析】假设10月初鸡蛋价格10元,11月初鸡蛋价格比10月初上涨了15%,11月初鸡蛋价格是10月初的(1+15%),10月初鸡蛋价格×11月初对应百分率=11月初鸡蛋价格;再将11月初鸡蛋价格看作单位“1”,12月初比11月初回落了10%,12月初鸡蛋价格是11月初的(1-10%),11月初鸡蛋价格×12月初对应百分率=12月初鸡蛋价格,比较即可确定涨了还是跌了,12月初与10月初鸡蛋价格的差÷10月初鸡蛋价格=涨百分之几。
【详解】假设10月初鸡蛋价格10元。
10×(1+15%)×(1-10%)
=10×1.15×0.9
=10.35(元)
10.35>10
(10.35-10)÷10
=0.35÷10
=3.5%
答:12月初鸡蛋价格与10月初比是涨了,涨了3.5%。
【点睛】关键是确定单位“1”,整体数量×部分对应百分率=部分数量,差÷较小数=增加百分之几。
4.300千米
【分析】将公路总长看成单位“1”,两周共修25%+,用两周修的实际长度÷对应分率或百分率即可。
【详解】135÷(25%+)
=135÷0.45
=300(千米)
答:这段公路一共有300千米。
【点睛】关键是确定单位“1”,部分数量÷对应分率或百分率=整体数量。
5.5.3%
【分析】用100元的圆形纪念币除以2000元的圆形纪念币的质量再乘100%计算即可。
【详解】8÷150×100%
≈0.053×100%
=5.3%
答:面额为100元的圆形金质纪念币质量是面额为2000元的圆形金质纪念币质量的5.3%。
【点睛】本题关键在于对一个数是另一个数的百分之几的求法,这里用除法计算。
6.7389套
【分析】将去年生产数量看作单位“1”,去年生产数量×今年前4个月的产量对应百分率=今年前4个月的产量;一年有12个月,4个月占全年的,再将今年生产数量看作单位“1”,今年前4个月的产量÷对应分率=今年生产数量,据此列式解答。
【详解】3284×75%÷
=3284×0.75÷
=2463×
=7389(套)
答:今年可生产童装7389套。
【点睛】关键是确定单位“1”,整体数量×部分对应百分率=部分数量,部分数量÷对应分率=整体数量。
7.(1)13人;
(2)20%;
(3)六年级学生参加社会实践活动人数变化呈上升趋势
【分析】(1)把六(1)班8~12月参加社会实践活动的总人数除以5即可;
(2)六(2)班12月参加社会实践活动的人数比六(1)班多百分之几,用多的人数除以六(1)班12月参加社会实践活动的人数即可;
(3)根据折线统计图可知,六年级学生参加社会实践活动人数每个月的数量都在增加,即人数变化呈上升趋势。
【详解】(1)(8+10+12+15+20)÷5
=65÷5
=13(人)
答:六(1)班8~12月平均每个月参加社会实践活动的有13人。
(2)(24﹣20)÷20
=4÷20
=20%
答:六(2)班12月参加社会实践活动的人数比六(1)班多百分之二十。
(3)根据折线统计图可知,六年级学生参加社会实践活动人数变化呈上升趋势。
【点睛】此题主要考查的是如何从折线统计图中获取信息,然后再根据信息进行计算、分析、解答即可。
8.6000米
【分析】把这条公路长看作单位“1”,设这条公路全长x米,则第一天修了15%x米,第二天修了15%x×+15%x米,根据两天共修了2100米列方程解答。
【详解】解:设这条公路全长x米,根据题意得:
15%x+15%x×+15%x=2100
x+x+x=2100
x=2100
x=2100÷
x=6000
答:这条公路全长6000米。
【点睛】此题考查的是列方程解决问题,解答此题关键是求出第二天修的长度。
9.6分;理由见详解
【分析】先根据求一个数比另一个数多百分之几,用相差数除以另一个数再乘100%,则用李叔叔实际的速度减去规定的时速,然后用它们的差除以规定的时速再乘100%,最后观察结果在哪个扣分范围即可。
【详解】理由如下:
(100-80)÷80×100%
=20÷80×100%
=25%
20%<25%<50%
答:李叔叔将被扣6分。
【点睛】本题考查了百分数的应用,明确求一个数比另一个数多百分之几,用除法计算。
10.1200米
【分析】把公路总长看作单位“1” ,用剩下的810米除以对应的分率是1-20%-即可求出公路长。
【详解】810÷(1-20%-)
=810÷
=1200(米)
答:这条乡村公路有1200米。
【点睛】此题考查的是分数除法的应用,找准单位“1”,明确求单位“1”的量用除法是解题关键。
11.40元
【分析】把这件羽绒服的原价看作单位“1”,先提价20%,提价后的价格是原价的(1+20%),单位“1”已知,用乘法求出提价后的价格;
又降价10%出售,再把提价后的价格看作单位“1”,降价后的价格是提价后价格的(1-10%),单位“1”已知,用乘法求出现价;
最后用现价减去原价,就是现在一件羽绒服赚的钱数。
【详解】现价:
500×(1+20%)×(1-10%)
=500×1.2×0.9
=600×0.9
=540(元)
赚了:540-500=40(元)
答:现在一件羽绒服赚40元。
【点睛】本题考查百分数的应用,区分两个单位“1”的不同,明确求比一个数多或少百分之几的数是多少,用乘法计算。
12.1820元
【分析】医疗费用共计7500元,已经超过6000元,在起付线以上的部分是(7500-400)元,按80%报销,则自己要付20%,即要交付(7500-400)×(1-80%)元,再加上起付线的钱数,最终求出王爷爷所需付的钱数。
【详解】(7500-400)×(1-80%)+400
=7100×0.2+400
=1420+400
=1820(元)
答:王爷爷只需自己付1820元。
【点睛】此题主要是找到关键节点6000元,按不同的标准报销,掌握求一个数的百分之几是多少的计算方法。
13.75页
【详解】解:设这本书一共有x页.
20%x+15=x
x =75
答:这本书一共有75页.
14.7.5%
【分析】根据求一个数比另一个数多(少)百分之几,用相差数除以另一个数再乘100%,则用(4000-3700)÷4000×100%即可求出原计划手机出货量比实际手机出货量少百分之几。
【详解】(4000-3700)÷4000×100%
=300÷4000×100%
=7.5%
答:原计划手机出货量比实际手机出货量少7.5%。
【点睛】本题主要考查了百分数的应用,明确求一个数比另一个数多(少)百分之几,用除法计算。
15.格子布中白色部分的面积是总面积的58%
【详解】试题分析:如图一共有3×3=9个格子,所以可得每个格子布的面积是图面积的9倍,格子布白色部分的面积也是图上白色面积的9倍,下图中白色部分所占面积的百分比=0.58=58%,据此即可解答.
解:=0.58=58%,
答:格子布中白色部分的面积是总面积的58%.
点评:解答此题的关键是明确每个格子中白色部分占格子的面积的百分比,就是这块布中白色的面积占总面积的百分之几.
16.60个
【分析】求一个数的几分之几是多少,用乘法,先用10乘,求出第二天吃的个数;把这筐苹果的总个数看作单位“1”,用1减去还剩下的70%,即两天吃了(1-70%),对应着两天吃了的个数,根据百分数除法的意义,用两天吃的总个数除以(1-70%),即可求出这筐苹果原来有多少个。
【详解】(10+10×)÷(1-70%)
=(10+8)÷30%
=18÷0.3
=60(个)
答:这筐苹果原来有60个。
【点睛】求一个数的几分之几是多少,用乘法计算;已知一个数的百分之几是多少,求这个数,用除法计算。
17.(1)1008万吨
(2)907.2万吨
【分析】(1)要求630万辆机动车全年的二氧化碳排放总量,需先求1辆机动车全年二氧化碳的排放量,列式为,为计算方便,将换算为,再进一步求出630万辆机动车全年的二氧化碳排放总量。
(2)降低一成到一成五,表示的含义就是降低10%到15%,也就是最少降低10%,由此可知该市2021年机动车的二氧化碳排放量预计不超过(万吨)。
【详解】(1)
(万吨)
答:该市2019年年底保有的机动车在2020年排放二氧化碳约1008万吨。
(2)
(万吨)
答:该市2021年机动车的二氧化碳排放量预计不超过907.2万吨。
【点睛】百分数运算的实际应用,需要我们熟悉百分数的意义及其计算方法;此外,从“克”到“吨”的转化,再到万吨,其中的计算稍显复杂,要细心一些;第二问求的是不超过多少万吨,因此不必将降低一成五的效果也计算出来,只要计算出降低一成的就可以。
18.216千米
【分析】将甲车速度看作单位“1”,那么乙车速度是甲车的(1-20%),据此利用乘法求出乙车的速度,从而利用减法求出速度差。根据题意,两车相遇时,甲车的路程比乙车多了(24×2)千米,将路程差除以速度差,求出甲车的行驶时间。根据“速度×时间=路程”求出甲车路程,再减去甲多行的24千米,求出A、B两地的距离即可。
【详解】乙车速度:
80×(1-20%)
=80×80%
=64(千米/时)
甲车每小时比乙车多行:80-64=16(千米)
甲车行驶时间:24×2÷16=3(小时)
两地路程:
80×3-24
=240-24
=216(千米)
答:A、B两地间的路程是216千米。
【点睛】本题考查了含百分数的运算、行程问题中的相遇问题。求比一个数少百分之几的数是多少,用乘法;路程差÷速度差=时间。
19.(1)120人 (2)90人 (3)174人
【详解】(1)1500×8%=120(人)
(2)120×(1-25%)=90(人)
(3)120×(1+45%)=174(人)
20.600千米
【分析】由题意可知,下午行了210千米,这时已行路程和剩下路程的比是3∶1,即此时已行的路程占总路程的,即210千米占总路程的(-40%),再根据除法的意义,用除法计算即可。
【详解】210÷(-40%)
=210÷
=210×
=600(千米)
答:A、B两城之间相距600千米。
【点睛】本题考查分数除法,明确部分的量除以所对应的分率等于单位“1”的量是解题的关键。
21.(1)50平方厘米
(2)大:125平方厘米;小:100平方厘米
【分析】已知两个长方形重叠部分的面积相当于小长方形面积的,相当于大长方形面积的20%。
(1)又知小长方形的面积是40平方厘米,则可先求得重叠部分面积,把小长方形的面积看作单位“1”,根据求一个数的几分之几是多少,用乘法计算,列式为:40×=10(平方厘米);
因为重叠部分面积相当于大长方形的20%,把大长方形的面积看作单位“1”,根据已知一个数的百分之几是多少,求这个数用除法计算,列式为10÷20%,综合算式为:40×÷20%;
(2)如果重叠部分的面积是25平方厘米,把小长方形的面积看作单位“1”,根据已知一个数的几分之几是多少,求这个数用除法计算,可知:要求得小长方形的面积,列式为:25÷;
把大长方形的面积看作单位“1”,根据已知一个数的百分之几是多少,求这个数用除法计算,要求得大正方形的面积,列式为:25÷20%。
【详解】(1)40×÷20%
=10÷0.2
=50(平方厘米)
答:大长方形的面积是50平方厘米。
(2)25÷=25×4=100(平方厘米)
25÷20%=125(平方厘米)
答:大长方形的面积是125平方厘米;小长方形的面积是100平方厘米。
【点睛】主要考查了单位“1”未知在分数除法中、百分数除法中的应用,需要理解:量÷对应分率=单位“1”的量。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
