第5单元圆达标练习(含答案)数学六年级上册人教版
文档属性
| 名称 | 第5单元圆达标练习(含答案)数学六年级上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 21:00:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第5单元圆达标练习-数学六年级上册人教版
一、选择题
1.下面的图形中,涂色部分不是扇形的是( )。
A. B. C. D.
2.一只挂钟的时针长1dm,从上午9时到下午3时,时针尖端所走的路程是( )dm。
A.1.57 B.3.14 C.6.28 D.5.14
3.如图所示,将半径为4cm和5cm的两个半圆形叠放在一起,,为圆心。阴影部分的总周长为( )cm。
A.19.42 B.34.26 C.37.26 D.38.26
4.把一个直径为6dm的圆形纸片剪成两个半圆,每个半圆的面积是( )dm2。
A.28.26 B.14.13 C.15.42 D.9.42
5.大圆直径是小圆直径的3倍,那么小圆面积是大圆面积的( )。
A. B. C.3倍 D.9倍
6.如图圆的半径是1cm,计算阴影部分面积下列算法正确的是( )。
A.3.14×2-2×1 B.
C. D.
二、填空题
7.在长10cm,宽7cm的长方形内画一个最大的圆,它的半径是( )厘米,周长是( )厘米。
8.在一个长1.25m、宽0.8m的长方形里,最多能画( )个半径20cm的圆。
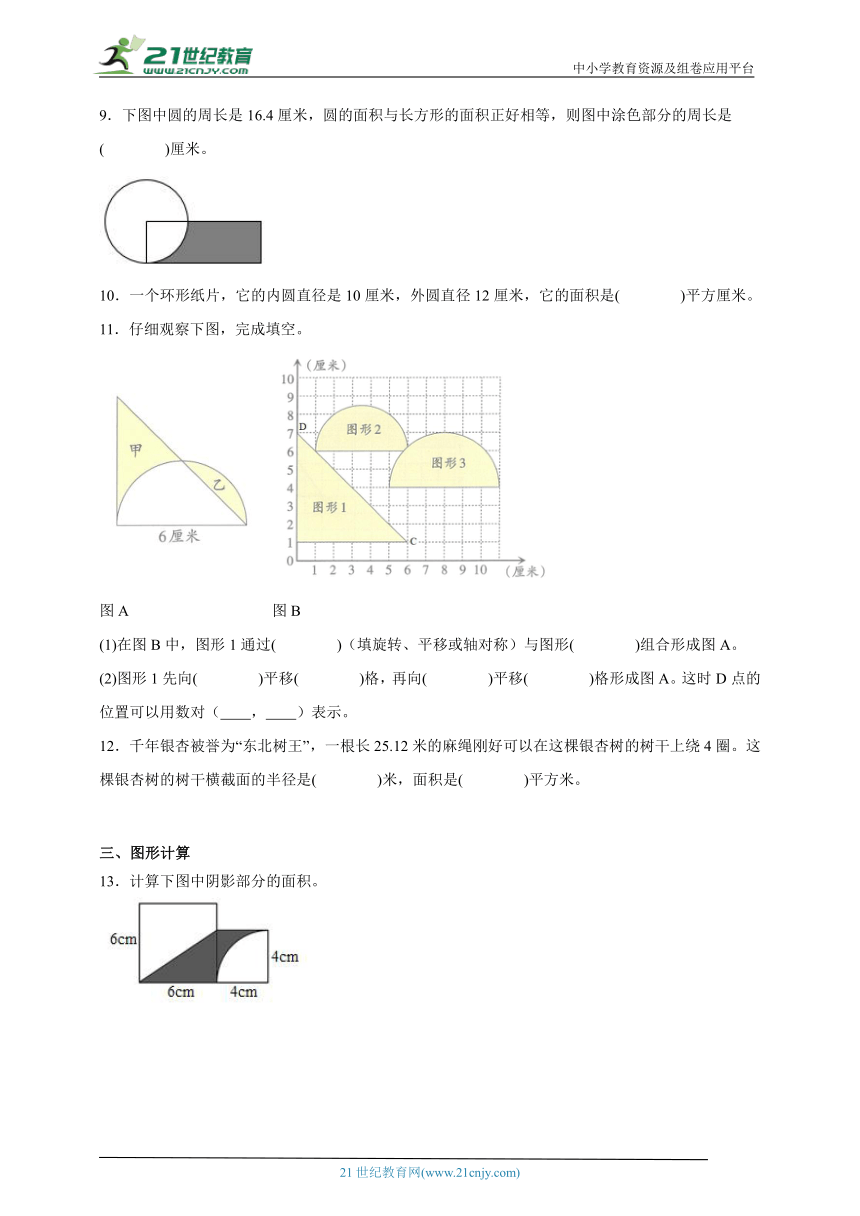
9.下图中圆的周长是16.4厘米,圆的面积与长方形的面积正好相等,则图中涂色部分的周长是( )厘米。
10.一个环形纸片,它的内圆直径是10厘米,外圆直径12厘米,它的面积是( )平方厘米。
11.仔细观察下图,完成填空。
图A 图B
(1)在图B中,图形1通过( )(填旋转、平移或轴对称)与图形( )组合形成图A。
(2)图形1先向( )平移( )格,再向( )平移( )格形成图A。这时D点的位置可以用数对( , )表示。
12.千年银杏被誉为“东北树王”,一根长25.12米的麻绳刚好可以在这棵银杏树的树干上绕4圈。这棵银杏树的树干横截面的半径是( )米,面积是( )平方米。
三、图形计算
13.计算下图中阴影部分的面积。
14.计算下面图形阴影部分的面积。
四、解答题
15.小亮家到少年宫的距离是3768米,他骑一辆车轮外直径大约是60厘米的自行车去少年宫.按车轮每分钟转100圈计算,他骑这辆车去少年宫大约需要多少分钟?
16.周日,乐乐从家出发去圆圆家。
(1)乐乐家在圆圆家( )偏( )( )方向,距离( )千米。
(2)两人从圆圆家出发去距离圆圆家8千米的图书馆。请你画出以圆圆家为圆心8千米为半径的圆。
(3)以圆圆家为圆心,乐乐家与图书馆构成的扇形的面积是50.24平方千米,请在图中标出图书馆B的具体位置,∠AOB=( )。
17.一天,小军和小芳到一个近似于圆的公园游玩,两人突然想到一个数学问题:“这个公园的面积大约是多少平方米?”经过探究,两人想出了一个好办法:两人沿着公园的A点处同时出发,背向而跑,如图。小军的速度是164米/分钟,小芳的速度是150米/分钟,经过2分钟两人相遇。你能按他们的办法算出这个公园的面积吗?试一试。
18.数学的对称美在图形中多有体现,如下面左图所示。
(1)用圆规将左图画在方格纸上。
(2)左图阴影部分的面积是多少平方厘米?
19.一个圆形牛栏的直径是16米,现在把这个牛栏的四周加宽2米,现在的牛栏比原来的牛栏多多少平方米?至少需要多少米长的粗铁丝才能把现在的牛栏围上5圈?
20.一个圆形花坛的直径是20米,在里面种植红、黄两种颜色的花,红花与黄花的种植面积之比为3∶2。
(1)这个花坛的面积有多大?
(2)种植红花与黄花的面积分别是多少?
参考答案:
1.B
【分析】一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,据此判断即可。
【详解】由分析可知:
涂色部分不是扇形的是B项。
故答案为:B
【点睛】此题考查了扇形的定义,要熟练掌握。
2.B
【分析】下午3时转换成24小时计时法是3+12=15时,从9时到15时经过了15-9=6小时,时针每小时走一个格子是30°,6小时走过6×30=180°,时针走过的路程就是一个半径为1dm,圆心角为180°的圆弧的长度,也是圆的周长的一半。
【详解】3.14×2×1×
=6.28×
=3.14(分米)
时针尖端所走的路程是3.14分米。
故答案为:B
【点睛】此题主要考查弧长的求法,掌握24小时计时法与普通计时法的互化也是解题的关键。
3.D
【分析】由图可知,阴影部分的周长=小圆周长的一半+小圆的半径+大圆周长的一半+大圆半径+大圆半径与小圆半径的差,已知两圆各自的半径,用公式:圆周长的一半=πr,分别计算出数量关系中的长度再相加即可,据此解答。
【详解】根据分析:
4×3.14+4+5×3.14+5+(5-4)
=12.56+4+15.7+5+1
=16.56+15.7+6
=32.26+6
=38.26(cm)
所以,这个阴影部分的总周长为38.26cm。
故答案为:D
【点睛】此题考查了求阴影部分的周长,关键计算时不能数漏边数。
4.B
【分析】圆的面积=,据此解答即可。
【详解】6÷2=3(分米)
3.14×3×3÷2
=28.26÷2
=14.13(平方分米)
故答案为:B
【点睛】本题考查圆的面积,解答本题的关键是掌握圆的面积计算公式。
5.A
【分析】假设出小圆的直径,表示出大圆的直径,利用“”表示出小圆和大圆的面积,最后用除法求出小圆面积占大圆面积的分率,据此解答。
【详解】假设小圆直径为,则大圆直径为。
=
=
÷
=÷
=×
=
所以,小圆面积是大圆面积的。
故答案为:A
【点睛】熟练掌握圆的面积计算公式并表示出大圆和小圆的面积是解答题目的关键。
6.B
【分析】由图可知,正方形的面积=等腰直角三角形的面积×2,阴影部分的面积=圆的面积-正方形的面积,据此解答。
【详解】
3.14×12-(1×2)×1÷2×2
=3.14×12-2×1÷2×2
=3.14-2
=1.14(平方厘米)
故答案为:B
【点睛】掌握阴影部分面积的计算方法是解答题目的关键。
7. 3.5 21.98
【分析】在一个长方形中画一个最大的圆,圆的直径等于长方形短边的长,因为长方形的短边为7厘米,所以圆的直径为7厘米,先求出半径,再根据圆的周长公式求出周长即可。
【详解】7÷2=3.5(厘米)
3.14×7=21.98(厘米)
【点睛】解答此题应明确:在长方形中画一个最大的圆,圆的直径等于长方形短边的长。
8.6
【分析】先看长方形的长能画几个圆,宽可以画几个圆,再相乘求出最多能画几个圆即可。
【详解】圆的直径20×2=40厘米=0.4米
0.8÷0.4=2(个)
1.25÷0.4≈3(个)
2×3=6(个)
【点睛】本题考查圆、长方形的特征,解答本题的关键是掌握圆的特征。
9.20.5
【分析】观察图形可知,圆的半径=长方形的宽,圆的面积=长方形的面积=长×宽;圆的面积=π×半径×半径,长方形的长=π×半径×半径÷半径=π×半径;弧长等于圆周长的,图中涂色部分的周长=圆的周长+2×长方形的长+长方形的宽-长方形的宽=圆的周长+2×长方形的长=圆的周长+2π×半径=圆的周长+圆的周长,即可解答。
【详解】设圆的半径为r,则圆的面积=长方形面积=πr2,长方形的长=πr2÷r=πr
涂色部分周长=×2πr+πr+r+πr-r
=×2πr+2πr
=×16.4+16.4
=20.5(厘米)
【点睛】本题考查圆的周长公式、长方形周长公式、圆的面积和长方形面积公式的运用。
10.34.54
【分析】由题意可知,就是求圆环的面积根据“S环形=π(R2-r2)”进行解答即可
【详解】10÷2=5(厘米);
12÷2=6(厘米);
3.14×(62-52)
=3.14×11
=34.54(平方厘米)
【点睛】熟练掌握求圆环面积的公式是解答本题的关键。
11.(1) 平移 3
(2) 右 5 上 3 5 10
【分析】(1)物体或图形在同一平面内沿直线运动,而本身没有发生大小、形状和方向上的改变,像这样的物体或图形所做的运动叫做平移;物体或图形绕着一个点或一个轴运动,像这样的物体或图形所做的运动叫做旋转。把一个图形沿着某一条直线折叠,如果它能与另一个图形完全重合,那么就说这两个图形关于这条直线对称,叫轴对称。
图形1是两条直角边长都是6厘米的直角三角形,图形2是直径为5厘米的半圆,图形3是直径为6厘米的半圆,图形1的直角边长等于图形3的直径,根据平移的特点可知:在图B中,图形1通过平移与图形3组合形成图A。
(2)通过观察发现:图形1的直角顶点,向右平移5格,再向上平移3格,能够与图形3的直径的左端点重合。所以,在图B中,可以把图形1先向右平移5格,再向上平移3格,与图形3组合形成图A。也可以把图形1先向上平移3格,再向右平移5格,与图形3组合形成图A。
用数对表示物体的位置时,先说列,后说行,表示形式为(列数,行数)。据此可知:原来D点的位置是(0,7),平移后0+5=5,7+3=10,所以平移后,D点就移到了第5列、第10行的交点处,用数对表示是(5,10)。
【详解】(1)在图B中,图形1通过平移与图形3组合形成图A。
(2)图形1先向右平移5格,再向上平移3格形成图A。(或者图形1先向上平移3格,再向右平移5格形成图A。)这时D点的位置可以用数对(5,10)表示。
12. 1 3.14
【分析】根据题意,用25.12÷4,求出麻绳绕这棵银杏树的树干1圈的长度,也就是这个树干的周长,再根据圆的周长公式:周长=π×半径×2,半径=周长÷2÷π,代入数据,求出树干横截面的半径;再根据圆的面积公式:面积=π×半径2。代入数据,即可解答。
【详解】25.12÷4=6.28(米)
6.28÷2÷3.14
=3.14÷3.14
=1(米)
3.14×12
=3.14×1
=3.14(平方米)
千年银杏被誉为“东北树王”,一根长25.12米的麻绳刚好可以在这棵银杏树的树干上绕4圈。这棵银杏树的树干横截面的半径是1米,面积是3.14平方米。
13.15.44平方厘米
【分析】观察图意可知,阴影部分的面积等于三角形的面积加上小正方形的面积减去四分之一圆的面积。根据三角形、正方形和圆的面积计算公式解题即可。
【详解】6×4÷2+4×4-×3.14×42
=12+16-×3.14×16
=12+16-12.56
=15.44(cm2)
14.0.86平方分米
【分析】阴影部分的面积可用边长为2分米的正方形面积减去半径为1分米的圆的面积,据此解答即可。
【详解】
(平方分米)
【点睛】本题考查组合图形,解答本题的关键是掌握圆、正方形的面积公式。
15.他骑这辆车去少年宫大约需要20分钟.
【详解】自行车轮胎的外直径已知,从而可以求出其周长,进而可以求出每分钟所行的距离;用家到学校的距离除以自行车每分钟行的距离,就是所需的时间.
60厘米=0.6米
3768÷(3.14×0.6×100)
=3768÷188.4
=20(分钟)
答:他骑这辆车去少年宫大约需要20分钟.
16.(1)南;西;30°;8
(2)图形见详解
(3)图形见详解;90°
【分析】(1)观察图形可知,图上1格表示2千米,则乐乐家到圆圆家的距离为2×4=8千米,再根据“上北下南,左西右东”及角度信息填空即可;
(2)以圆圆家为圆心,8千米为半径据此作圆即可;
(3)根据圆的面积公式:S=πr2,据此求出半径为8千米的圆的面积,再用50.24除以圆的面积,最后乘360°进而找到图书馆的位置和∠AOB的度数。
【详解】(1)2×4=8(千米)
则乐乐家在圆圆家南偏西30°方向,距离8千米。
(2)如图所示:
(3)3.14×82
=3.14×64
=200.96(平方千米)
50.24÷200.96×360°
=0.25×360°
=90°
则∠AOB=90°
如图所示:
【点睛】本题考查圆的认识和圆的面积,明确圆的特征和熟记圆的面积公式是解题的关键。
17.31400平方米
【分析】两人相遇时,路程和就是圆的周长。路程和=速度和×相遇时间,据此求出路程和,即圆的周长。将圆周长除以2再除以3.14,求出圆的半径。圆面积=3.14×半径2,据此列式求出圆的直径,即这个公园的面积。
【详解】(164+150)×2
=314×2
=628(米)
628÷2÷3.14=100(米)
3.14×1002=31400(平方米)
答:这个公园的面积是31400平方米。
【点睛】本题考查了圆的周长和面积,熟记并灵活运用圆的周长和面积公式是解题关键。
18.(1)画图:见详解
(2)25.12平方厘米
【分析】(1)先画一个半径为8÷2=4(厘米)的大圆,再画两个半径为4÷2=2(厘米)的圆周长的一半即可。
(2)画一条辅助线,将左边的小阴影部分移到右边的小空白部分,则整个阴影部分变为半径为4厘米的圆的面积一半,由此解答即可。
【详解】(1)如图:
(2)3.14×(8÷2) ÷2
=3.14×16÷2
=25.12(平方厘米);
【点睛】解答本题的关键是要仔细观察图形,看看它是由什么基本图形组成的,进而画出来。再求阴影部分的面积时,画辅助线是关键。
19.113.04平方米;314米
【分析】增加的形状是个圆环,确定大圆和小圆半径,根据圆环面积=π(R2-r2),求出比原来多的面积;第二问,根据圆的周长=2πr,求出大圆一周的长度,乘5即可。
【详解】16÷2=8(米)
8+2=10(米)
3.14×(102-82)
=3.14×(100-64)
=3.14×36
=113.04(平方米)
2×3.14×10=62.8(米)
62.8×5=314(米)
答:现在的牛栏比原来的牛栏多113.04平方米,至少需要314米长的粗铁丝才能把现在的牛栏围上5圈。
【点睛】关键是掌握并灵活运用圆环面积公式和圆的周长公式。
20.(1)314平方米
(2)红花188.4平方米;黄花125.6平方米
【分析】(1)根据圆的直径计算出圆的半径,利用圆的面积公式计算;
(2)红花占花坛总面积的,黄花占花坛总面积的,根据按比例分配解答即可。
【详解】(1)半径:20÷2=10(米)
3.14×10×10=314(平方米)
答:这个花坛的面积是314平方米。
(2)红花种植面积:314×=188.4(平方米)
黄花种植面积:314×=125.6(平方米)
答:种植红花188.4平方米,种植黄花125.6平方米。
【点睛】本题主要综合考查了圆的面积和比的应用相关知识点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第5单元圆达标练习-数学六年级上册人教版
一、选择题
1.下面的图形中,涂色部分不是扇形的是( )。
A. B. C. D.
2.一只挂钟的时针长1dm,从上午9时到下午3时,时针尖端所走的路程是( )dm。
A.1.57 B.3.14 C.6.28 D.5.14
3.如图所示,将半径为4cm和5cm的两个半圆形叠放在一起,,为圆心。阴影部分的总周长为( )cm。
A.19.42 B.34.26 C.37.26 D.38.26
4.把一个直径为6dm的圆形纸片剪成两个半圆,每个半圆的面积是( )dm2。
A.28.26 B.14.13 C.15.42 D.9.42
5.大圆直径是小圆直径的3倍,那么小圆面积是大圆面积的( )。
A. B. C.3倍 D.9倍
6.如图圆的半径是1cm,计算阴影部分面积下列算法正确的是( )。
A.3.14×2-2×1 B.
C. D.
二、填空题
7.在长10cm,宽7cm的长方形内画一个最大的圆,它的半径是( )厘米,周长是( )厘米。
8.在一个长1.25m、宽0.8m的长方形里,最多能画( )个半径20cm的圆。
9.下图中圆的周长是16.4厘米,圆的面积与长方形的面积正好相等,则图中涂色部分的周长是( )厘米。
10.一个环形纸片,它的内圆直径是10厘米,外圆直径12厘米,它的面积是( )平方厘米。
11.仔细观察下图,完成填空。
图A 图B
(1)在图B中,图形1通过( )(填旋转、平移或轴对称)与图形( )组合形成图A。
(2)图形1先向( )平移( )格,再向( )平移( )格形成图A。这时D点的位置可以用数对( , )表示。
12.千年银杏被誉为“东北树王”,一根长25.12米的麻绳刚好可以在这棵银杏树的树干上绕4圈。这棵银杏树的树干横截面的半径是( )米,面积是( )平方米。
三、图形计算
13.计算下图中阴影部分的面积。
14.计算下面图形阴影部分的面积。
四、解答题
15.小亮家到少年宫的距离是3768米,他骑一辆车轮外直径大约是60厘米的自行车去少年宫.按车轮每分钟转100圈计算,他骑这辆车去少年宫大约需要多少分钟?
16.周日,乐乐从家出发去圆圆家。
(1)乐乐家在圆圆家( )偏( )( )方向,距离( )千米。
(2)两人从圆圆家出发去距离圆圆家8千米的图书馆。请你画出以圆圆家为圆心8千米为半径的圆。
(3)以圆圆家为圆心,乐乐家与图书馆构成的扇形的面积是50.24平方千米,请在图中标出图书馆B的具体位置,∠AOB=( )。
17.一天,小军和小芳到一个近似于圆的公园游玩,两人突然想到一个数学问题:“这个公园的面积大约是多少平方米?”经过探究,两人想出了一个好办法:两人沿着公园的A点处同时出发,背向而跑,如图。小军的速度是164米/分钟,小芳的速度是150米/分钟,经过2分钟两人相遇。你能按他们的办法算出这个公园的面积吗?试一试。
18.数学的对称美在图形中多有体现,如下面左图所示。
(1)用圆规将左图画在方格纸上。
(2)左图阴影部分的面积是多少平方厘米?
19.一个圆形牛栏的直径是16米,现在把这个牛栏的四周加宽2米,现在的牛栏比原来的牛栏多多少平方米?至少需要多少米长的粗铁丝才能把现在的牛栏围上5圈?
20.一个圆形花坛的直径是20米,在里面种植红、黄两种颜色的花,红花与黄花的种植面积之比为3∶2。
(1)这个花坛的面积有多大?
(2)种植红花与黄花的面积分别是多少?
参考答案:
1.B
【分析】一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,据此判断即可。
【详解】由分析可知:
涂色部分不是扇形的是B项。
故答案为:B
【点睛】此题考查了扇形的定义,要熟练掌握。
2.B
【分析】下午3时转换成24小时计时法是3+12=15时,从9时到15时经过了15-9=6小时,时针每小时走一个格子是30°,6小时走过6×30=180°,时针走过的路程就是一个半径为1dm,圆心角为180°的圆弧的长度,也是圆的周长的一半。
【详解】3.14×2×1×
=6.28×
=3.14(分米)
时针尖端所走的路程是3.14分米。
故答案为:B
【点睛】此题主要考查弧长的求法,掌握24小时计时法与普通计时法的互化也是解题的关键。
3.D
【分析】由图可知,阴影部分的周长=小圆周长的一半+小圆的半径+大圆周长的一半+大圆半径+大圆半径与小圆半径的差,已知两圆各自的半径,用公式:圆周长的一半=πr,分别计算出数量关系中的长度再相加即可,据此解答。
【详解】根据分析:
4×3.14+4+5×3.14+5+(5-4)
=12.56+4+15.7+5+1
=16.56+15.7+6
=32.26+6
=38.26(cm)
所以,这个阴影部分的总周长为38.26cm。
故答案为:D
【点睛】此题考查了求阴影部分的周长,关键计算时不能数漏边数。
4.B
【分析】圆的面积=,据此解答即可。
【详解】6÷2=3(分米)
3.14×3×3÷2
=28.26÷2
=14.13(平方分米)
故答案为:B
【点睛】本题考查圆的面积,解答本题的关键是掌握圆的面积计算公式。
5.A
【分析】假设出小圆的直径,表示出大圆的直径,利用“”表示出小圆和大圆的面积,最后用除法求出小圆面积占大圆面积的分率,据此解答。
【详解】假设小圆直径为,则大圆直径为。
=
=
÷
=÷
=×
=
所以,小圆面积是大圆面积的。
故答案为:A
【点睛】熟练掌握圆的面积计算公式并表示出大圆和小圆的面积是解答题目的关键。
6.B
【分析】由图可知,正方形的面积=等腰直角三角形的面积×2,阴影部分的面积=圆的面积-正方形的面积,据此解答。
【详解】
3.14×12-(1×2)×1÷2×2
=3.14×12-2×1÷2×2
=3.14-2
=1.14(平方厘米)
故答案为:B
【点睛】掌握阴影部分面积的计算方法是解答题目的关键。
7. 3.5 21.98
【分析】在一个长方形中画一个最大的圆,圆的直径等于长方形短边的长,因为长方形的短边为7厘米,所以圆的直径为7厘米,先求出半径,再根据圆的周长公式求出周长即可。
【详解】7÷2=3.5(厘米)
3.14×7=21.98(厘米)
【点睛】解答此题应明确:在长方形中画一个最大的圆,圆的直径等于长方形短边的长。
8.6
【分析】先看长方形的长能画几个圆,宽可以画几个圆,再相乘求出最多能画几个圆即可。
【详解】圆的直径20×2=40厘米=0.4米
0.8÷0.4=2(个)
1.25÷0.4≈3(个)
2×3=6(个)
【点睛】本题考查圆、长方形的特征,解答本题的关键是掌握圆的特征。
9.20.5
【分析】观察图形可知,圆的半径=长方形的宽,圆的面积=长方形的面积=长×宽;圆的面积=π×半径×半径,长方形的长=π×半径×半径÷半径=π×半径;弧长等于圆周长的,图中涂色部分的周长=圆的周长+2×长方形的长+长方形的宽-长方形的宽=圆的周长+2×长方形的长=圆的周长+2π×半径=圆的周长+圆的周长,即可解答。
【详解】设圆的半径为r,则圆的面积=长方形面积=πr2,长方形的长=πr2÷r=πr
涂色部分周长=×2πr+πr+r+πr-r
=×2πr+2πr
=×16.4+16.4
=20.5(厘米)
【点睛】本题考查圆的周长公式、长方形周长公式、圆的面积和长方形面积公式的运用。
10.34.54
【分析】由题意可知,就是求圆环的面积根据“S环形=π(R2-r2)”进行解答即可
【详解】10÷2=5(厘米);
12÷2=6(厘米);
3.14×(62-52)
=3.14×11
=34.54(平方厘米)
【点睛】熟练掌握求圆环面积的公式是解答本题的关键。
11.(1) 平移 3
(2) 右 5 上 3 5 10
【分析】(1)物体或图形在同一平面内沿直线运动,而本身没有发生大小、形状和方向上的改变,像这样的物体或图形所做的运动叫做平移;物体或图形绕着一个点或一个轴运动,像这样的物体或图形所做的运动叫做旋转。把一个图形沿着某一条直线折叠,如果它能与另一个图形完全重合,那么就说这两个图形关于这条直线对称,叫轴对称。
图形1是两条直角边长都是6厘米的直角三角形,图形2是直径为5厘米的半圆,图形3是直径为6厘米的半圆,图形1的直角边长等于图形3的直径,根据平移的特点可知:在图B中,图形1通过平移与图形3组合形成图A。
(2)通过观察发现:图形1的直角顶点,向右平移5格,再向上平移3格,能够与图形3的直径的左端点重合。所以,在图B中,可以把图形1先向右平移5格,再向上平移3格,与图形3组合形成图A。也可以把图形1先向上平移3格,再向右平移5格,与图形3组合形成图A。
用数对表示物体的位置时,先说列,后说行,表示形式为(列数,行数)。据此可知:原来D点的位置是(0,7),平移后0+5=5,7+3=10,所以平移后,D点就移到了第5列、第10行的交点处,用数对表示是(5,10)。
【详解】(1)在图B中,图形1通过平移与图形3组合形成图A。
(2)图形1先向右平移5格,再向上平移3格形成图A。(或者图形1先向上平移3格,再向右平移5格形成图A。)这时D点的位置可以用数对(5,10)表示。
12. 1 3.14
【分析】根据题意,用25.12÷4,求出麻绳绕这棵银杏树的树干1圈的长度,也就是这个树干的周长,再根据圆的周长公式:周长=π×半径×2,半径=周长÷2÷π,代入数据,求出树干横截面的半径;再根据圆的面积公式:面积=π×半径2。代入数据,即可解答。
【详解】25.12÷4=6.28(米)
6.28÷2÷3.14
=3.14÷3.14
=1(米)
3.14×12
=3.14×1
=3.14(平方米)
千年银杏被誉为“东北树王”,一根长25.12米的麻绳刚好可以在这棵银杏树的树干上绕4圈。这棵银杏树的树干横截面的半径是1米,面积是3.14平方米。
13.15.44平方厘米
【分析】观察图意可知,阴影部分的面积等于三角形的面积加上小正方形的面积减去四分之一圆的面积。根据三角形、正方形和圆的面积计算公式解题即可。
【详解】6×4÷2+4×4-×3.14×42
=12+16-×3.14×16
=12+16-12.56
=15.44(cm2)
14.0.86平方分米
【分析】阴影部分的面积可用边长为2分米的正方形面积减去半径为1分米的圆的面积,据此解答即可。
【详解】
(平方分米)
【点睛】本题考查组合图形,解答本题的关键是掌握圆、正方形的面积公式。
15.他骑这辆车去少年宫大约需要20分钟.
【详解】自行车轮胎的外直径已知,从而可以求出其周长,进而可以求出每分钟所行的距离;用家到学校的距离除以自行车每分钟行的距离,就是所需的时间.
60厘米=0.6米
3768÷(3.14×0.6×100)
=3768÷188.4
=20(分钟)
答:他骑这辆车去少年宫大约需要20分钟.
16.(1)南;西;30°;8
(2)图形见详解
(3)图形见详解;90°
【分析】(1)观察图形可知,图上1格表示2千米,则乐乐家到圆圆家的距离为2×4=8千米,再根据“上北下南,左西右东”及角度信息填空即可;
(2)以圆圆家为圆心,8千米为半径据此作圆即可;
(3)根据圆的面积公式:S=πr2,据此求出半径为8千米的圆的面积,再用50.24除以圆的面积,最后乘360°进而找到图书馆的位置和∠AOB的度数。
【详解】(1)2×4=8(千米)
则乐乐家在圆圆家南偏西30°方向,距离8千米。
(2)如图所示:
(3)3.14×82
=3.14×64
=200.96(平方千米)
50.24÷200.96×360°
=0.25×360°
=90°
则∠AOB=90°
如图所示:
【点睛】本题考查圆的认识和圆的面积,明确圆的特征和熟记圆的面积公式是解题的关键。
17.31400平方米
【分析】两人相遇时,路程和就是圆的周长。路程和=速度和×相遇时间,据此求出路程和,即圆的周长。将圆周长除以2再除以3.14,求出圆的半径。圆面积=3.14×半径2,据此列式求出圆的直径,即这个公园的面积。
【详解】(164+150)×2
=314×2
=628(米)
628÷2÷3.14=100(米)
3.14×1002=31400(平方米)
答:这个公园的面积是31400平方米。
【点睛】本题考查了圆的周长和面积,熟记并灵活运用圆的周长和面积公式是解题关键。
18.(1)画图:见详解
(2)25.12平方厘米
【分析】(1)先画一个半径为8÷2=4(厘米)的大圆,再画两个半径为4÷2=2(厘米)的圆周长的一半即可。
(2)画一条辅助线,将左边的小阴影部分移到右边的小空白部分,则整个阴影部分变为半径为4厘米的圆的面积一半,由此解答即可。
【详解】(1)如图:
(2)3.14×(8÷2) ÷2
=3.14×16÷2
=25.12(平方厘米);
【点睛】解答本题的关键是要仔细观察图形,看看它是由什么基本图形组成的,进而画出来。再求阴影部分的面积时,画辅助线是关键。
19.113.04平方米;314米
【分析】增加的形状是个圆环,确定大圆和小圆半径,根据圆环面积=π(R2-r2),求出比原来多的面积;第二问,根据圆的周长=2πr,求出大圆一周的长度,乘5即可。
【详解】16÷2=8(米)
8+2=10(米)
3.14×(102-82)
=3.14×(100-64)
=3.14×36
=113.04(平方米)
2×3.14×10=62.8(米)
62.8×5=314(米)
答:现在的牛栏比原来的牛栏多113.04平方米,至少需要314米长的粗铁丝才能把现在的牛栏围上5圈。
【点睛】关键是掌握并灵活运用圆环面积公式和圆的周长公式。
20.(1)314平方米
(2)红花188.4平方米;黄花125.6平方米
【分析】(1)根据圆的直径计算出圆的半径,利用圆的面积公式计算;
(2)红花占花坛总面积的,黄花占花坛总面积的,根据按比例分配解答即可。
【详解】(1)半径:20÷2=10(米)
3.14×10×10=314(平方米)
答:这个花坛的面积是314平方米。
(2)红花种植面积:314×=188.4(平方米)
黄花种植面积:314×=125.6(平方米)
答:种植红花188.4平方米,种植黄花125.6平方米。
【点睛】本题主要综合考查了圆的面积和比的应用相关知识点。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
