第6单元比的认识达标练习(含答案)数学六年级上册北师大版
文档属性
| 名称 | 第6单元比的认识达标练习(含答案)数学六年级上册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 21:07:21 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第6单元比的认识达标练习-数学六年级上册北师大版
一、选择题
1.轿车和面包车从甲、乙两地同时出发,相向而行,轿车到达乙地用了20小时,面包车到达甲地用了25小时,轿车和面包车速度的最简比是( )。
A.20∶25 B.25∶20 C.4∶5 D.5∶4
2.一个直角三角形,它的一个锐角与直角度数比是2∶5 ,则另一个锐角与直角度数的比是( )。
A.2∶3 B.3∶5 C.3∶2 D.5∶3
3.如图,阴影部分的面积相当于甲圆面积的,相当于乙圆面积的,那么乙的空白部分与甲的空白部分的面积比是( )。
A.6∶1 B.5∶4 C.4∶5 D.5∶6
4.一个周长是12米的长方形,长与宽的比是2∶1,这个长方形的面积是( )。
A.24平方米 B.16平方米 C.12平方米 D.8平方米
5.一种盐水有120克,盐和水的比是1∶5,如果再放入5克盐,那么盐和水的比是( )。
A.4∶1 B.1∶3 C.1∶4 D.1∶5
6.作为防疫使用的84消毒水,消毒液和水的体积比为,按照这个配比。配505毫升的消毒水需要( )毫升的消毒液。
A.5 B.5.5 C.100 D.500
二、填空题
7.柳树与杨树的比是4∶5,那么柳树比杨树少,杨树比柳树多。
8.一个长方形的周长是36cm,长和宽的比是5∶4,这个长方形面积是( )cm 。
9.植树节,六年级女生和男生共同去植树,女生和男生植树棵数的比是3∶5,男生植树150棵,则女生植树( )棵。
10.六年级把一批图书按5:4:3分配给一班、二班和三班.已知一班比三班多分得12本,这批图书共有( )本.
11.某工厂今年第一季度生产洗衣机4000台,其中一月份生产的台数占总数的,二月份与三月份生产的台数比是,该工厂三月份生产了( )台洗衣机。
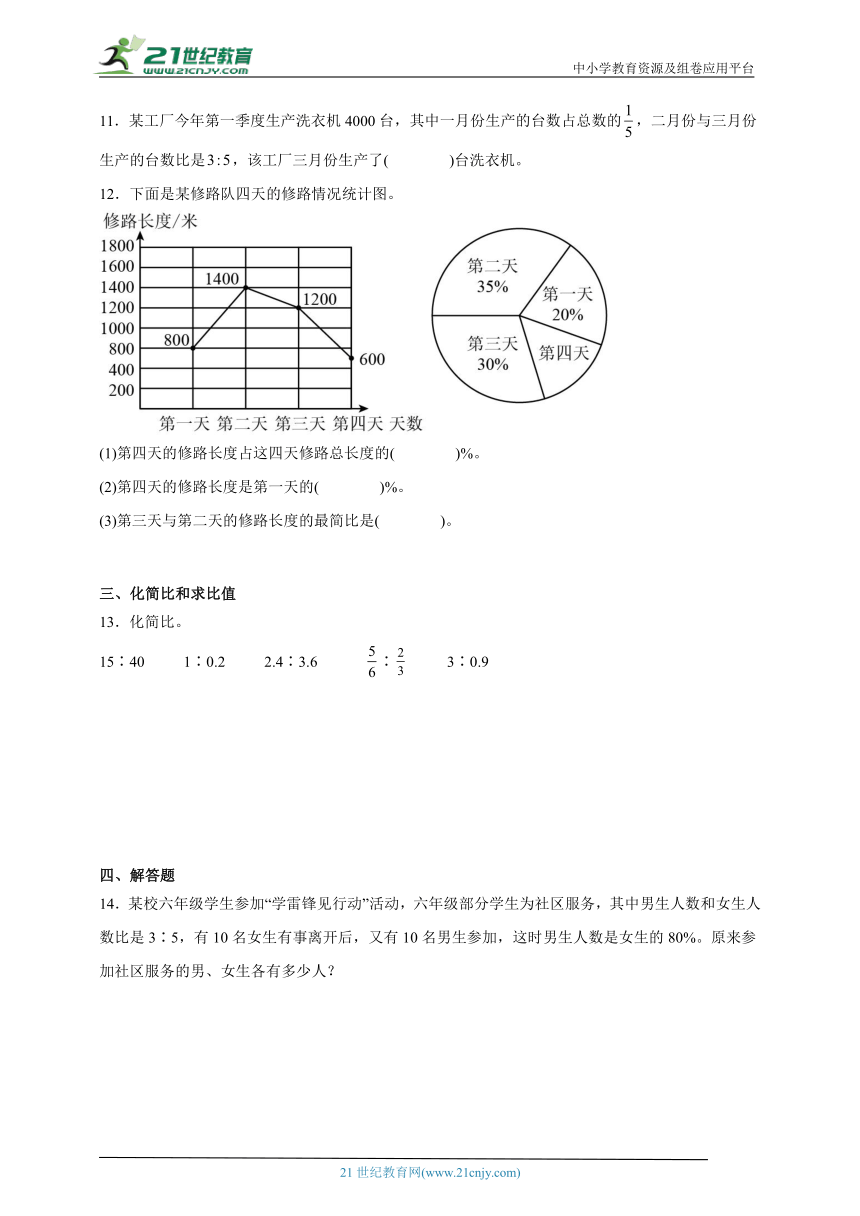
12.下面是某修路队四天的修路情况统计图。
(1)第四天的修路长度占这四天修路总长度的( )%。
(2)第四天的修路长度是第一天的( )%。
(3)第三天与第二天的修路长度的最简比是( )。
三、化简比和求比值
13.化简比。
15∶40 1∶0.2 2.4∶3.6 ∶ 3∶0.9
四、解答题
14.某校六年级学生参加“学雷锋见行动”活动,六年级部分学生为社区服务,其中男生人数和女生人数比是3∶5,有10名女生有事离开后,又有10名男生参加,这时男生人数是女生的80%。原来参加社区服务的男、女生各有多少人?
15.学校新购买了一批桌椅.一套桌椅的价钱是90元,其中椅子的价钱和桌子的价钱的比是7:11,桌子和椅子的价钱分别是多少元?
16.二维码支付因其简便、安全、快捷的性能,在生活中很受大家欢迎。卖早餐的王阿姨根据需求,在摊位边上贴了收款二维码,某天早上,通过二维码收款和现金收款的比是3∶2,其中通过二维码收款219元,这天早上通过现金收款多少元?
17.甲、乙两仓库都存有粮食,后来甲仓库增加存粮88吨,乙仓库运出20%存粮,这时甲仓库与乙仓库存粮的质量比是7∶6,已知乙仓库原来存粮300吨,甲仓库原来存粮多少吨?
18.学校买来文艺书、科技书和故事书三种图书,其中是文艺书,科技书与故事书的本数的比是5∶3,已知科技书买了60本。学校这三种书共买了多少本?
19.一艘轮船以每时40千米的速度从甲港驶往乙港,行了全程的20%后,又行时。这时,未行的路程与已行的路程的比是,甲、乙两港相距多少千米?
20.2022年第22届世界杯足球赛在卡塔尔举行,比赛用球是中国生产的。足球的表面一般是由正五边形和正六边形皮拼接围成的,正五边形皮和正六边形皮块数的比是3∶5,且正五边形皮比正六边形皮少8块。两种形状的球皮各有多少块?
参考答案:
1.D
【分析】把甲、乙两地的距离看作单位“1”,根据路程÷时间=速度,据此可知轿车的速度为,面包车的速度为,据此求出轿车和面包车的速度比即可。
【详解】∶
=(×100)∶(×100)
=5∶4
则轿车和面包车的速度比是5∶4。
故答案为:D
【点睛】本题考查比的意义,明确路程、时间和速度之间的关系是解题的关键。
2.B
【分析】直角三角形中两个锐角的和是一个直角;根据“一个锐角与直角的度数比是2∶5”,把一个锐角看做2份,那另一个锐角是(5-2)份,直角是5份;由此列式解答即可。
【详解】根据一个锐角与直角的度数比是2∶5,把一个锐角看做2份,直角是5份,那另一个锐角是:5-2=3(份),则另一个锐角与直角度数的比是:3∶5;
故答案为:B。
【点睛】解答此题的关键是理解直角三角形中两个锐角的和为90°。
3.C
【分析】根据题意“阴影部分的面积相当于甲圆面积的”可得:甲圆面积是阴影部分面积的6倍,由“阴影部分的面积相当于乙圆面积的”可得:乙圆面积是阴影部分面积的5倍,然后根据题意,进行比即可。
【详解】由分析知:甲圆面积是阴影部分面积的6倍,则甲圆空白部分是阴影部分的(6-1)倍,乙圆面积是阴影部分面积的5倍,则乙圆的空白部分是阴影部分的(5-1)倍,则乙的空白部分与甲的空白部分的面积比是(5-1)∶(6-1)=4∶5。
故答案为:C
【点睛】解答此题应进行转化,转化为都是一个数的几倍,然后在统一标准下进行比即可。
4.D
【分析】先求出长方形长与宽的和(长方形的周长÷2=长+宽);再把长与宽的和按2∶1分配,分别求出长方形的长、宽;最后求出长方形的面积(长方形的面积=长×宽)。
【详解】12÷2=6(米)
2+1=3(份)
6÷3=2(米)
宽:2×1=2(米)
长:2×2=4(米)
面积:4×2=8(平方米)
所以这个长方形的面积是8平方米。
故答案为:D
【点睛】注意求长方形的长和宽时不能把长方形的周长按比分配,因为长方形的周长包含两个长和两个宽。
5.C
【分析】用原来的盐水质量÷总份数,求出一份数,一份数分别乘盐和水的对应份数,求出原来的盐和水,(原来的盐+放入的盐)∶水,化简即可。
【详解】120÷(1+5)
=120÷6
=20(克)
20×1=20(克)
20×5=100(克)
(20+5)∶100
=25∶100
=1∶4
故答案为:C
【点睛】关键是理解比的意义,先求出原来的盐和水,再根据比的意义写出比,化简。
6.A
【分析】由“消毒液与水按的比例配制成消毒水”可知消毒液占消毒水总质量的,然后根据分数乘法的意义求出配制505毫升消毒水需要多少消毒液。
【详解】
(毫升)
配505毫升的消毒水需要5毫升的消毒液。
故答案为:A
【点睛】解答此题的关键是找准对应量,根据数量关系,列式解答即可。
7.;
【分析】把柳树的棵数看作“4”,则杨树的棵数是“5”,求柳树比杨树少几分之几,用柳树比杨树少的棵数除以杨树棵数;求杨树比柳树多几分之几,用杨树比柳树多的棵数除以柳树棵数。
【详解】(5-4)÷5
=1÷5
=
(5-4)÷4
=1÷4
=
柳树比杨树少,杨树比柳树多。
【点睛】求一个数比另一个数多或少几分之几,用这两数之差除以另一个数。关键是柳树与杨树棵数的比,求出柳树、杨树的“棵数”。
8.80
【分析】用长方形的周长除以2,求出一条长和宽长度的和,再根据按比例分配的方法求出长方形的长和宽,再根据长方形的面积公式进行计算。
【详解】长方形的长:
(36÷2)×
=18×
=10(cm)
长方形的宽:
(36÷2)×
=18×
=8(cm)
这个长方形面积:10×8=80(cm2)
【点睛】本题的关键是求出一条长和宽的长度和是多少,再根据按比例分配的方法求出长方形的长和宽。
9.90
【分析】女生和男生植树棵数的比是3∶5,即女生有3份,男生有5份,已知男生植树150棵,用150除以男生的份数5,即可求出1份的数量,再用1份数量乘女生的份数即可解答。
【详解】150÷5×3
=30×3
=90(棵)
植树节,六年级女生和男生共同去植树,女生和男生植树棵数的比是3∶5,男生植树150棵,则女生植树90棵。
【点睛】本题考查了比的应用,关键是求出一份的棵树。
10.72
【解析】略
11.2000
【分析】一月份生产的台数占总数的,则二月份与三月份共生产的台数占总数的1-,也就是4000×(1-)台;又二月份与三月份生产的台数比是,则三月份生产的台数占二月份与三月份生产的台数的,根据乘法的意义,用4000×(1-)×即可求出三月份生产的台数;据此解答。
【详解】4000×(1-)×
=4000××
=2000(台)
该工厂三月份生产了2000台洗衣机。
【点睛】本题主要考查比的应用,求出二月份与三月份共生产的台数是解题的关键。
12.(1)15
(2)75
(3)6∶7
【分析】(1)把这条路的总长看作单位“1”,用1减去第一天修路长度占这条路的百分比,减去第二天修路长度占这条路的百分比,减去第三天修路长度占这条路的百分比,即可求出第四天修路长度占这四天修路总长度的百分比;
(2)用第四天修路长度除以第一天修路的长度即可解答;
(3)根据比的意义,用第三天修路的长度∶第二天修路的长度,化简,即可解答。
【详解】(1)1-35%-20%-30%
=65%-20%-30%
=45%-30%
=15%
第四天的修路长度占这四天修路总长度的15%。
(2)600÷800=75%
第四天的修路长度是第一天的75%。
(3)1200∶1400
=(1200÷200)∶(1400÷200)
=6∶7
第三天与第二天的修路长度的最简比是6∶7。
【点睛】本题考查折线统计图和扇形统计图的应用,并且考查根据统计图提供的信息解答问题的能力,
13.3∶8;5∶1;2∶3;5∶4;10∶3
【分析】化简比根据比的基本性质作答,即比的前项和后项同时乘或除以一个相同的数(0除外),比值不变。注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数。
【详解】15∶40
=(15÷5)∶(40÷5)
=3∶8
1∶0.2
=(1×5)∶(0.2×5)
=5∶1
2.4∶3.6
=(2.4÷1.2)∶(3.6÷1.2)
=2∶3
∶
=(×6)∶(×6)
=5∶4
3∶0.9
=(3÷0.3)∶(0.9÷0.3)
=10∶3
14.男生:54人;女生:90人
【分析】原来男生人数和女生人数比是3∶5,那么男生人数就是总人数的,后来又有10名男生参加,有10名女生有事离开总人数不变,男生人数是女生的80%,那么男生人数就是总人数的80%÷(1+80%),男生人数增加了总人数的80%÷(1+80%)-,它对应的数量是10人,根据分数除法的意义即可求出总人数,进而求出原来男女生的人数。
【详解】
=144(人)
(人)
(人)
答:原来参加区服务的男、女生各有54人、90人。
【点睛】此题考查的目的是理解掌握比的意义及应用,关键是抓住总人数不变,把单位“1”统一到不变的总人数,再根据分数除法的意义求出总人数,进而求出原来的男生、女生人数。
15.7+11=18(份),
90×,
,
答:桌子的价钱是55元,椅子的价钱是35元.
【详解】首先求出总份数,用它作公分母,用比的各项分别作分子求出椅子、桌子的价钱各总钱数的几分之几,然后根据一个数乘分数的意义,用乘法解答.
16.146元
【分析】二维码收款和现金收款的比是3∶2,把二维码收款的钱数看作3份,现金收款的钱数看作2份,已知通过二维码收款219元,用二维码收款的219元除以二维码收款的钱数对应的份数,求出1份量是多少元,再乘现金收款对应的份数,即可求出这天早上通过现金收款多少元。
【详解】219÷3×2
=73×2
=146(元)
答:这天早上通过现金收款146元。
【点睛】此题主要考查比的应用,解题关键是求出1份量是多少元。
17.192吨
【分析】先把乙仓库原来的存粮看作单位“1”,乙仓库运出20%存粮,则还剩下(1-20%),用乙仓库原来的粮食量乘(1-20%)就是后来的乙仓库的质量,后来甲仓库与乙仓库的质量比是7∶6,把乙仓库的质量看成6份,甲仓库的质量就是7份,用后来乙仓库的质量除以6,求出1份是多少吨,再乘7就是甲仓库后来的质量,然后减去88吨,就是甲仓库原来的质量。
【详解】
=192(吨)
答:甲仓库原来存粮192吨。
【点睛】先根据两者后来的比,根据按照按比分配的方法,求出甲仓库后来的质量,然后再进一步解答即可。
18.120本
【分析】科技书与故事书的本数的比是5∶3,把科技书的本数看作5份,故事书的本数看作3份,已知科技书买了60本,用除法计算得出1份的本数,再得出科技书与故事书的总本数,三种图书中是文艺书,则科技书与故事书的总本数占(1-),用除法计算即可得解。
【详解】
=120(本)
答:学校这三种书共买了120本。
【点睛】本题主要考查了比的应用,关键是得出科技书与故事书的总本数。
19.1200千米
【分析】将甲、乙两港的总路程看成单位“1”,根据未行的路程与已行的路程的比是可得:已行的路程占总路程的,再根据已行的路程等于全程的20%与时行程的和,求出时的行程占总路程的-20%;根据速度×时间=路程求出时的行程,再除以其占总路程的分率即可求出总路程;据此解答。
【详解】×40÷(-20%)
=×40÷5%
=60÷5%
=1200(千米)
答:甲、乙两港相距1200千米。
【点睛】根据未行路程与已行路程的比求出已行路程占全程的分率是完成本题的关键。
20.正五边形:12块;正六边形:20块。
【分析】正五边形皮比正六边形皮少8块,由“正五边形皮和正六边形皮块数的比是3∶5”可知,正五边形皮的块数比正六边形皮的块数少(5-3)份,已知正五边形皮比正六边形皮少8块,先用除法求出1份的块数,即8÷(5-3);再用乘法分别求出3份(正五边形)、5份正六边形的皮块的数量。
【详解】8÷(5-3)
=8÷2
=4(块)
4×3=12(块)
4×5=20(块)
答:正五边形皮有12块,正六边形皮有20块。
【点睛】本题考查比的应用,两种形状球皮的相差的块数、相差的份数已知,关键是根据除法求出1份的块数,进而求出3份、5份的块数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元比的认识达标练习-数学六年级上册北师大版
一、选择题
1.轿车和面包车从甲、乙两地同时出发,相向而行,轿车到达乙地用了20小时,面包车到达甲地用了25小时,轿车和面包车速度的最简比是( )。
A.20∶25 B.25∶20 C.4∶5 D.5∶4
2.一个直角三角形,它的一个锐角与直角度数比是2∶5 ,则另一个锐角与直角度数的比是( )。
A.2∶3 B.3∶5 C.3∶2 D.5∶3
3.如图,阴影部分的面积相当于甲圆面积的,相当于乙圆面积的,那么乙的空白部分与甲的空白部分的面积比是( )。
A.6∶1 B.5∶4 C.4∶5 D.5∶6
4.一个周长是12米的长方形,长与宽的比是2∶1,这个长方形的面积是( )。
A.24平方米 B.16平方米 C.12平方米 D.8平方米
5.一种盐水有120克,盐和水的比是1∶5,如果再放入5克盐,那么盐和水的比是( )。
A.4∶1 B.1∶3 C.1∶4 D.1∶5
6.作为防疫使用的84消毒水,消毒液和水的体积比为,按照这个配比。配505毫升的消毒水需要( )毫升的消毒液。
A.5 B.5.5 C.100 D.500
二、填空题
7.柳树与杨树的比是4∶5,那么柳树比杨树少,杨树比柳树多。
8.一个长方形的周长是36cm,长和宽的比是5∶4,这个长方形面积是( )cm 。
9.植树节,六年级女生和男生共同去植树,女生和男生植树棵数的比是3∶5,男生植树150棵,则女生植树( )棵。
10.六年级把一批图书按5:4:3分配给一班、二班和三班.已知一班比三班多分得12本,这批图书共有( )本.
11.某工厂今年第一季度生产洗衣机4000台,其中一月份生产的台数占总数的,二月份与三月份生产的台数比是,该工厂三月份生产了( )台洗衣机。
12.下面是某修路队四天的修路情况统计图。
(1)第四天的修路长度占这四天修路总长度的( )%。
(2)第四天的修路长度是第一天的( )%。
(3)第三天与第二天的修路长度的最简比是( )。
三、化简比和求比值
13.化简比。
15∶40 1∶0.2 2.4∶3.6 ∶ 3∶0.9
四、解答题
14.某校六年级学生参加“学雷锋见行动”活动,六年级部分学生为社区服务,其中男生人数和女生人数比是3∶5,有10名女生有事离开后,又有10名男生参加,这时男生人数是女生的80%。原来参加社区服务的男、女生各有多少人?
15.学校新购买了一批桌椅.一套桌椅的价钱是90元,其中椅子的价钱和桌子的价钱的比是7:11,桌子和椅子的价钱分别是多少元?
16.二维码支付因其简便、安全、快捷的性能,在生活中很受大家欢迎。卖早餐的王阿姨根据需求,在摊位边上贴了收款二维码,某天早上,通过二维码收款和现金收款的比是3∶2,其中通过二维码收款219元,这天早上通过现金收款多少元?
17.甲、乙两仓库都存有粮食,后来甲仓库增加存粮88吨,乙仓库运出20%存粮,这时甲仓库与乙仓库存粮的质量比是7∶6,已知乙仓库原来存粮300吨,甲仓库原来存粮多少吨?
18.学校买来文艺书、科技书和故事书三种图书,其中是文艺书,科技书与故事书的本数的比是5∶3,已知科技书买了60本。学校这三种书共买了多少本?
19.一艘轮船以每时40千米的速度从甲港驶往乙港,行了全程的20%后,又行时。这时,未行的路程与已行的路程的比是,甲、乙两港相距多少千米?
20.2022年第22届世界杯足球赛在卡塔尔举行,比赛用球是中国生产的。足球的表面一般是由正五边形和正六边形皮拼接围成的,正五边形皮和正六边形皮块数的比是3∶5,且正五边形皮比正六边形皮少8块。两种形状的球皮各有多少块?
参考答案:
1.D
【分析】把甲、乙两地的距离看作单位“1”,根据路程÷时间=速度,据此可知轿车的速度为,面包车的速度为,据此求出轿车和面包车的速度比即可。
【详解】∶
=(×100)∶(×100)
=5∶4
则轿车和面包车的速度比是5∶4。
故答案为:D
【点睛】本题考查比的意义,明确路程、时间和速度之间的关系是解题的关键。
2.B
【分析】直角三角形中两个锐角的和是一个直角;根据“一个锐角与直角的度数比是2∶5”,把一个锐角看做2份,那另一个锐角是(5-2)份,直角是5份;由此列式解答即可。
【详解】根据一个锐角与直角的度数比是2∶5,把一个锐角看做2份,直角是5份,那另一个锐角是:5-2=3(份),则另一个锐角与直角度数的比是:3∶5;
故答案为:B。
【点睛】解答此题的关键是理解直角三角形中两个锐角的和为90°。
3.C
【分析】根据题意“阴影部分的面积相当于甲圆面积的”可得:甲圆面积是阴影部分面积的6倍,由“阴影部分的面积相当于乙圆面积的”可得:乙圆面积是阴影部分面积的5倍,然后根据题意,进行比即可。
【详解】由分析知:甲圆面积是阴影部分面积的6倍,则甲圆空白部分是阴影部分的(6-1)倍,乙圆面积是阴影部分面积的5倍,则乙圆的空白部分是阴影部分的(5-1)倍,则乙的空白部分与甲的空白部分的面积比是(5-1)∶(6-1)=4∶5。
故答案为:C
【点睛】解答此题应进行转化,转化为都是一个数的几倍,然后在统一标准下进行比即可。
4.D
【分析】先求出长方形长与宽的和(长方形的周长÷2=长+宽);再把长与宽的和按2∶1分配,分别求出长方形的长、宽;最后求出长方形的面积(长方形的面积=长×宽)。
【详解】12÷2=6(米)
2+1=3(份)
6÷3=2(米)
宽:2×1=2(米)
长:2×2=4(米)
面积:4×2=8(平方米)
所以这个长方形的面积是8平方米。
故答案为:D
【点睛】注意求长方形的长和宽时不能把长方形的周长按比分配,因为长方形的周长包含两个长和两个宽。
5.C
【分析】用原来的盐水质量÷总份数,求出一份数,一份数分别乘盐和水的对应份数,求出原来的盐和水,(原来的盐+放入的盐)∶水,化简即可。
【详解】120÷(1+5)
=120÷6
=20(克)
20×1=20(克)
20×5=100(克)
(20+5)∶100
=25∶100
=1∶4
故答案为:C
【点睛】关键是理解比的意义,先求出原来的盐和水,再根据比的意义写出比,化简。
6.A
【分析】由“消毒液与水按的比例配制成消毒水”可知消毒液占消毒水总质量的,然后根据分数乘法的意义求出配制505毫升消毒水需要多少消毒液。
【详解】
(毫升)
配505毫升的消毒水需要5毫升的消毒液。
故答案为:A
【点睛】解答此题的关键是找准对应量,根据数量关系,列式解答即可。
7.;
【分析】把柳树的棵数看作“4”,则杨树的棵数是“5”,求柳树比杨树少几分之几,用柳树比杨树少的棵数除以杨树棵数;求杨树比柳树多几分之几,用杨树比柳树多的棵数除以柳树棵数。
【详解】(5-4)÷5
=1÷5
=
(5-4)÷4
=1÷4
=
柳树比杨树少,杨树比柳树多。
【点睛】求一个数比另一个数多或少几分之几,用这两数之差除以另一个数。关键是柳树与杨树棵数的比,求出柳树、杨树的“棵数”。
8.80
【分析】用长方形的周长除以2,求出一条长和宽长度的和,再根据按比例分配的方法求出长方形的长和宽,再根据长方形的面积公式进行计算。
【详解】长方形的长:
(36÷2)×
=18×
=10(cm)
长方形的宽:
(36÷2)×
=18×
=8(cm)
这个长方形面积:10×8=80(cm2)
【点睛】本题的关键是求出一条长和宽的长度和是多少,再根据按比例分配的方法求出长方形的长和宽。
9.90
【分析】女生和男生植树棵数的比是3∶5,即女生有3份,男生有5份,已知男生植树150棵,用150除以男生的份数5,即可求出1份的数量,再用1份数量乘女生的份数即可解答。
【详解】150÷5×3
=30×3
=90(棵)
植树节,六年级女生和男生共同去植树,女生和男生植树棵数的比是3∶5,男生植树150棵,则女生植树90棵。
【点睛】本题考查了比的应用,关键是求出一份的棵树。
10.72
【解析】略
11.2000
【分析】一月份生产的台数占总数的,则二月份与三月份共生产的台数占总数的1-,也就是4000×(1-)台;又二月份与三月份生产的台数比是,则三月份生产的台数占二月份与三月份生产的台数的,根据乘法的意义,用4000×(1-)×即可求出三月份生产的台数;据此解答。
【详解】4000×(1-)×
=4000××
=2000(台)
该工厂三月份生产了2000台洗衣机。
【点睛】本题主要考查比的应用,求出二月份与三月份共生产的台数是解题的关键。
12.(1)15
(2)75
(3)6∶7
【分析】(1)把这条路的总长看作单位“1”,用1减去第一天修路长度占这条路的百分比,减去第二天修路长度占这条路的百分比,减去第三天修路长度占这条路的百分比,即可求出第四天修路长度占这四天修路总长度的百分比;
(2)用第四天修路长度除以第一天修路的长度即可解答;
(3)根据比的意义,用第三天修路的长度∶第二天修路的长度,化简,即可解答。
【详解】(1)1-35%-20%-30%
=65%-20%-30%
=45%-30%
=15%
第四天的修路长度占这四天修路总长度的15%。
(2)600÷800=75%
第四天的修路长度是第一天的75%。
(3)1200∶1400
=(1200÷200)∶(1400÷200)
=6∶7
第三天与第二天的修路长度的最简比是6∶7。
【点睛】本题考查折线统计图和扇形统计图的应用,并且考查根据统计图提供的信息解答问题的能力,
13.3∶8;5∶1;2∶3;5∶4;10∶3
【分析】化简比根据比的基本性质作答,即比的前项和后项同时乘或除以一个相同的数(0除外),比值不变。注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数。
【详解】15∶40
=(15÷5)∶(40÷5)
=3∶8
1∶0.2
=(1×5)∶(0.2×5)
=5∶1
2.4∶3.6
=(2.4÷1.2)∶(3.6÷1.2)
=2∶3
∶
=(×6)∶(×6)
=5∶4
3∶0.9
=(3÷0.3)∶(0.9÷0.3)
=10∶3
14.男生:54人;女生:90人
【分析】原来男生人数和女生人数比是3∶5,那么男生人数就是总人数的,后来又有10名男生参加,有10名女生有事离开总人数不变,男生人数是女生的80%,那么男生人数就是总人数的80%÷(1+80%),男生人数增加了总人数的80%÷(1+80%)-,它对应的数量是10人,根据分数除法的意义即可求出总人数,进而求出原来男女生的人数。
【详解】
=144(人)
(人)
(人)
答:原来参加区服务的男、女生各有54人、90人。
【点睛】此题考查的目的是理解掌握比的意义及应用,关键是抓住总人数不变,把单位“1”统一到不变的总人数,再根据分数除法的意义求出总人数,进而求出原来的男生、女生人数。
15.7+11=18(份),
90×,
,
答:桌子的价钱是55元,椅子的价钱是35元.
【详解】首先求出总份数,用它作公分母,用比的各项分别作分子求出椅子、桌子的价钱各总钱数的几分之几,然后根据一个数乘分数的意义,用乘法解答.
16.146元
【分析】二维码收款和现金收款的比是3∶2,把二维码收款的钱数看作3份,现金收款的钱数看作2份,已知通过二维码收款219元,用二维码收款的219元除以二维码收款的钱数对应的份数,求出1份量是多少元,再乘现金收款对应的份数,即可求出这天早上通过现金收款多少元。
【详解】219÷3×2
=73×2
=146(元)
答:这天早上通过现金收款146元。
【点睛】此题主要考查比的应用,解题关键是求出1份量是多少元。
17.192吨
【分析】先把乙仓库原来的存粮看作单位“1”,乙仓库运出20%存粮,则还剩下(1-20%),用乙仓库原来的粮食量乘(1-20%)就是后来的乙仓库的质量,后来甲仓库与乙仓库的质量比是7∶6,把乙仓库的质量看成6份,甲仓库的质量就是7份,用后来乙仓库的质量除以6,求出1份是多少吨,再乘7就是甲仓库后来的质量,然后减去88吨,就是甲仓库原来的质量。
【详解】
=192(吨)
答:甲仓库原来存粮192吨。
【点睛】先根据两者后来的比,根据按照按比分配的方法,求出甲仓库后来的质量,然后再进一步解答即可。
18.120本
【分析】科技书与故事书的本数的比是5∶3,把科技书的本数看作5份,故事书的本数看作3份,已知科技书买了60本,用除法计算得出1份的本数,再得出科技书与故事书的总本数,三种图书中是文艺书,则科技书与故事书的总本数占(1-),用除法计算即可得解。
【详解】
=120(本)
答:学校这三种书共买了120本。
【点睛】本题主要考查了比的应用,关键是得出科技书与故事书的总本数。
19.1200千米
【分析】将甲、乙两港的总路程看成单位“1”,根据未行的路程与已行的路程的比是可得:已行的路程占总路程的,再根据已行的路程等于全程的20%与时行程的和,求出时的行程占总路程的-20%;根据速度×时间=路程求出时的行程,再除以其占总路程的分率即可求出总路程;据此解答。
【详解】×40÷(-20%)
=×40÷5%
=60÷5%
=1200(千米)
答:甲、乙两港相距1200千米。
【点睛】根据未行路程与已行路程的比求出已行路程占全程的分率是完成本题的关键。
20.正五边形:12块;正六边形:20块。
【分析】正五边形皮比正六边形皮少8块,由“正五边形皮和正六边形皮块数的比是3∶5”可知,正五边形皮的块数比正六边形皮的块数少(5-3)份,已知正五边形皮比正六边形皮少8块,先用除法求出1份的块数,即8÷(5-3);再用乘法分别求出3份(正五边形)、5份正六边形的皮块的数量。
【详解】8÷(5-3)
=8÷2
=4(块)
4×3=12(块)
4×5=20(块)
答:正五边形皮有12块,正六边形皮有20块。
【点睛】本题考查比的应用,两种形状球皮的相差的块数、相差的份数已知,关键是根据除法求出1份的块数,进而求出3份、5份的块数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
