组合图形的面积解决问题精选题提升篇(含答案)数学五年级上册北师大版
文档属性
| 名称 | 组合图形的面积解决问题精选题提升篇(含答案)数学五年级上册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 21:14:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
组合图形的面积解决问题精选题(提升篇)数学五年级上册北师大版
1.如下图,两个相同的直角三角形有一部分叠在一起.求阴影部分的面积.(单位:cm)
2.下图为小华家客厅平面图,想铺上地板,需要买多少平方米的地板?(想一想:怎样转化成以前学过的图形?你能想出用几种方法?)
3.求出组合图形的面积.
4.一条高速公路全长260千米,宽50米.这条公路占地多少公顷?合多少平方千米?
5.学校要做3面“文明中队”的锦旗(如下图所示).(单位:cm)
(1)一共需要布料多少平方分米?
(2)如果每平方米布料需要40元,做这些锦旗一共需要多少元?
6.下面三块地里种植了不同的蔬菜.黄瓜、西红柿和茄子各种植了多少平方米?这块地一共有多少公顷?
7.一张长方形的铁板,从长边的中点到两个宽边的中点分别连一条线,沿这两条线剪下来两个角.求剩下图形的面积是多少?
8.张叔叔购买一块钢板,形状规格如图。(单位:米)
(1)这块钢板的面积是多少平方米?
(2)如果每平方米钢板需要4.5元,购买这块钢板需要多少元?
9.有一块如图所示的铁板。
①求这块铁板的面积。
②如果给这块铁板涂油漆,需要油漆2.2千克,那么每千克油漆可以涂多少平方米?
10.下图是某山庄用木板制作的一个指示牌,现要给指示牌正反两面涂油漆。若每平方厘米用油漆6克,制作50个这样的指示牌共需油漆多少千克?
11.如下图,一张边长为4cm的正方形纸,从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩余部分面积是多少?
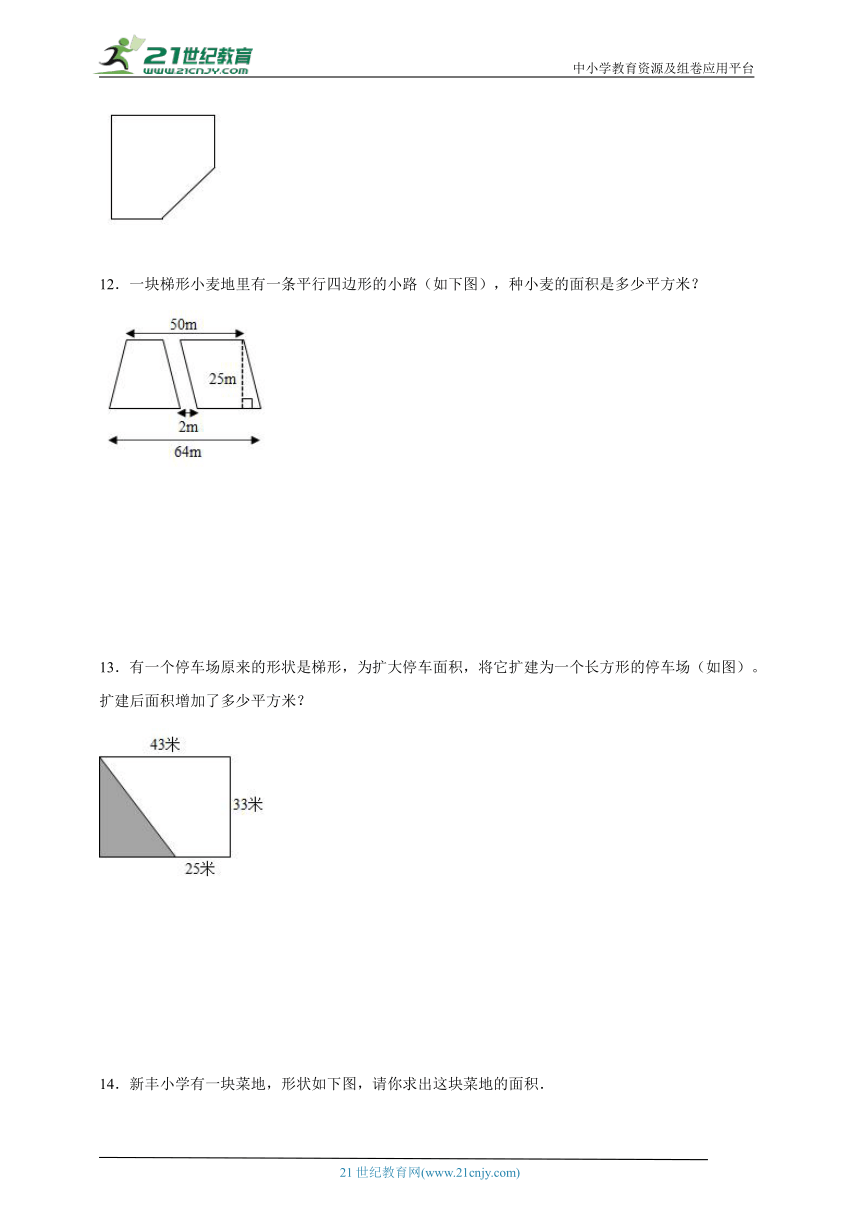
12.一块梯形小麦地里有一条平行四边形的小路(如下图),种小麦的面积是多少平方米?
13.有一个停车场原来的形状是梯形,为扩大停车面积,将它扩建为一个长方形的停车场(如图)。扩建后面积增加了多少平方米?
14.新丰小学有一块菜地,形状如下图,请你求出这块菜地的面积.
15.如图是由两个平行四边形组成的,这个图形的面积是多少?
16.阳光小学有一块空地(如下图)。
(1)算一算,这块空地的面积是多少平方米?
(2)学校计划在这块空地植上草皮,如果每平方米草皮的价格是12元,植满这块地需要多少元?
17.有一块面积为192平方米的菜地,正好可以分割成一块平行四边形菜地和一块直角三角形菜地(如下图).已知这块直角三角形菜地的两条直角边都是12米,则这块平行四边形菜地的高是多少米
18.一块梯形的苗圃种上百合和玫瑰(如图),阴影部分种的是百合,一共是1500平方米。这个梯形苗圃的面积是多少平方米?
19.下面是张大爷种的一块长方形菜地,涂色的部分种上了白菜,其余的地方种萝卜。请你算一下种白菜的面积。每平方米需施肥0.25千克,这块地共需施肥多少千克?
20.新丰学校有一块长方形草地,中间有两个小水池,其余的地方是草地,(如下图)草地的面积是多少平方米?
参考答案:
1.30cm2
【详解】[(9-6)+9]×5÷2=30(cm2)
2.33平方米;
【详解】略
3.5×5+5×2÷2=30(m2)
【详解】组合图形的面积=正方形的面积+三角形的面积=边长×边长+底×高÷2,代入对应的数字即可得出答案.
4.1300公顷;13平方千米
【详解】50米=0.05千米
260×0.05=13(km )
13×100=1300(公顷)
5.(1)40.5dm2 (2)16.2元
【详解】(1)30×50-30×10÷2=1350(cm2)=13.5(dm2) 13.5×3=40.5(dm2)
(2)40.5dm2=0.405(m2) 0.405×40=16.2(元)
6.茄子:240m2 黄瓜:800m2 西红柿:608m2 0.1648公顷
【详解】茄子:240m2 黄瓜:800m2 西红柿:608m2 240+800+608=1648(m2)=0.1648(公顷)
7.420cm2
【解析】略
8.(1)13平方米
(2)58.5元
【分析】(1)根据图示可知,求组合图形的面积可以转化为一个梯形的面积和一个长方形面积的和,利用梯形面积公式:S=(a+b)h÷2,以及长方形面积公式:S=ab,计算即可。
(2)用每平方米的单价乘面积,就是总钱数,据此解答即可。
【详解】(1)(3+5)×(3-1)÷2+5×1
=8+5
=13(平方米)
答:这块钢板的面积是13平方米。
(2)13×4.5=58.5(元)
答:购买这块钢板需要58.5元。
【点睛】本题主要考查组合图形的面积,关键是把不规则图形,转化为规则图形。
9.①6.6平方米;②3平方米
【分析】①根据长方形和梯形的面积公式,先分别计算铁板上下两个部分的面积,再相加求出铁板的面积;
②用铁板的面积6.6平方米除以2.2千克,求出每千克油漆可以涂多少平方米。
【详解】①(1.2+2.8)×1.2÷2+1.5×2.8
=4×1.2÷2+4.2
=2.4+4.2
=6.6(平方米)
答:这块铁板的面积是6.6平方米。
②6.6÷2.2=3(平方米)
答:每千克油漆可以涂3平方米。
【点睛】本题考查了组合图形的面积,掌握分割法求组合图形的面积是解题的关键。
10.240千克
【分析】如图:
将指示牌分成长方形与三角形两部分,求出面积和,乘2求出正反两面的面积;再乘每平方厘米用油漆的质量,即可求出一个指示牌需要油漆的质量,最后乘50即可得解。
【详解】(30×10+20×10÷2)×2×6×50
=400×2×6×50
=800×300
=240000(克)
240000克=240千克。
答:制作50个这样的指示牌共需油漆240千克。
【点睛】本题主要考查组合图形面积的求法,解题时注意单位的变化。
11.14平方厘米
【分析】正方形面积-剪下的三角形面积=剩余部分的面积。
【详解】
4×4-2×2÷2
=16-2
=14(平方厘米)
答:剩余部分面积是14平方厘米。
【点睛】本题主要考查组合图形的面积,此类问题一般通过割补法进行解答。
12.1375平方米
【分析】用梯形面积减去平行四边形的小路面积即可。
【详解】(50+64)×25÷2-2×25
=1425-50
=1375(平方米)
答:种小麦的面积是1375平方米。
【点睛】熟悉组合图形面积的一般计算方法为本题考查重点。
13.297平方米
【分析】观察图形可得:扩建后增加的面积等于底为(43-25)米、高为33米的三角形的面积,然后再根据三角形的面积公式S=ah÷2进行解答。
【详解】(43-25)×33÷2
=18×33÷2
=297(平方米)
答:扩建后面积增加了297平方米。
【点睛】解答求组合图形的面积,关键是观察分析图形是由哪几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答。
14.2250m2
【详解】60×34+35×12÷2=2250(m2)
15.22.5平方厘米
【详解】试题分析:由图意知:7.5厘米是2个平行四边形的高之和,这2个平行四边形的底相等,都是3厘米,所以这个图形的面积=2个平行四边形的面积之和=底×左边平行四边形的高+底×右边平行四边形的高=底×(左边平行四边形的高+右边平行四边形的高)=3×7.5.
解:3×7.5=22.5(平方厘米).
答:这个图形的面积是22.5平方厘米.
点评:解决本题的关键是由题意得出7.5厘米是2个平行四边形的高之和,这2个平行四边形的底相等,都是3厘米,再计算.
16.(1)56平方米;
(2)672元
【分析】(1)将图形分割如下:
原图形的面积=长方形的面积+梯形的面积,代入数据计算即可;
(2)用空地的面积×每平方米草皮的价格即可。
【详解】(1)8×4+(4+12-4)×(8-4)÷2
=32+12×4÷2
=32+24
=56(平方米)
答:这块空地的面积是56平方米。
(2)56×12=672(元)
答:植满这块地需要672元。
【点睛】本题主要考查求组合图形的面积,通常采用分割法。
17.10米
【分析】先求出三角形的面积,从这块地的面积里减去三角形的面积,再根据平行四边形的面积公式,求出平行四边形的高即可.
【详解】12×12÷2=72(平方米)(192-72)÷12=120÷12=10(米)
答:这块平行四边形菜地的高是10米.
18.2400平方米
【分析】由图可知,阴影部分三角形的高和梯形的高相等,根据百合花的种植面积求出梯形的高,最后利用“梯形的面积=(上底+下底)×高÷2”求出这个梯形苗圃的面积。
【详解】梯形的高:1500×2÷40
=3000÷40
=75(米)
面积:(24+40)×75÷2
=64×75÷2
=4800÷2
=2400(平方米)
答:这个梯形苗圃的面积是2400平方米。
【点睛】利用三角形的面积求出梯形的高是解答题目的关键。
19.4.4平方米;2.2千克
【详解】4×2.2=8.8(平方米)
8.8÷2=4.4(平方米)
8.8×0.25
=2.2×(4×0.25)
=2.2×1
=2.2(千克)
答:种白菜的面积是4.4平方米,共需施肥2.2千克。
【点睛】本题考查了三角形面积公式的应用和乘法的意义。
20.166平方米
【分析】观察图形可知,草地的面积=长方形的面积-正方形的面积-梯形的面积,根据长方形的面积=长×宽,正方形的面积=边长×边长,梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】长方形的面积:
20×10=200(平方米)
正方形的面积:
4×4=16(平方米)
梯形的面积:
(5+7)×3÷2
=12×3÷2
=18(平方米)
草地的面积:
200-16-18=166(平方米)
答:草地的面积是166平方米。
【点睛】本题考查组合图形面积的求法,先分析出组合图形是由哪些图形相加或相减得到,然后根据图形面积公式列式计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
组合图形的面积解决问题精选题(提升篇)数学五年级上册北师大版
1.如下图,两个相同的直角三角形有一部分叠在一起.求阴影部分的面积.(单位:cm)
2.下图为小华家客厅平面图,想铺上地板,需要买多少平方米的地板?(想一想:怎样转化成以前学过的图形?你能想出用几种方法?)
3.求出组合图形的面积.
4.一条高速公路全长260千米,宽50米.这条公路占地多少公顷?合多少平方千米?
5.学校要做3面“文明中队”的锦旗(如下图所示).(单位:cm)
(1)一共需要布料多少平方分米?
(2)如果每平方米布料需要40元,做这些锦旗一共需要多少元?
6.下面三块地里种植了不同的蔬菜.黄瓜、西红柿和茄子各种植了多少平方米?这块地一共有多少公顷?
7.一张长方形的铁板,从长边的中点到两个宽边的中点分别连一条线,沿这两条线剪下来两个角.求剩下图形的面积是多少?
8.张叔叔购买一块钢板,形状规格如图。(单位:米)
(1)这块钢板的面积是多少平方米?
(2)如果每平方米钢板需要4.5元,购买这块钢板需要多少元?
9.有一块如图所示的铁板。
①求这块铁板的面积。
②如果给这块铁板涂油漆,需要油漆2.2千克,那么每千克油漆可以涂多少平方米?
10.下图是某山庄用木板制作的一个指示牌,现要给指示牌正反两面涂油漆。若每平方厘米用油漆6克,制作50个这样的指示牌共需油漆多少千克?
11.如下图,一张边长为4cm的正方形纸,从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩余部分面积是多少?
12.一块梯形小麦地里有一条平行四边形的小路(如下图),种小麦的面积是多少平方米?
13.有一个停车场原来的形状是梯形,为扩大停车面积,将它扩建为一个长方形的停车场(如图)。扩建后面积增加了多少平方米?
14.新丰小学有一块菜地,形状如下图,请你求出这块菜地的面积.
15.如图是由两个平行四边形组成的,这个图形的面积是多少?
16.阳光小学有一块空地(如下图)。
(1)算一算,这块空地的面积是多少平方米?
(2)学校计划在这块空地植上草皮,如果每平方米草皮的价格是12元,植满这块地需要多少元?
17.有一块面积为192平方米的菜地,正好可以分割成一块平行四边形菜地和一块直角三角形菜地(如下图).已知这块直角三角形菜地的两条直角边都是12米,则这块平行四边形菜地的高是多少米
18.一块梯形的苗圃种上百合和玫瑰(如图),阴影部分种的是百合,一共是1500平方米。这个梯形苗圃的面积是多少平方米?
19.下面是张大爷种的一块长方形菜地,涂色的部分种上了白菜,其余的地方种萝卜。请你算一下种白菜的面积。每平方米需施肥0.25千克,这块地共需施肥多少千克?
20.新丰学校有一块长方形草地,中间有两个小水池,其余的地方是草地,(如下图)草地的面积是多少平方米?
参考答案:
1.30cm2
【详解】[(9-6)+9]×5÷2=30(cm2)
2.33平方米;
【详解】略
3.5×5+5×2÷2=30(m2)
【详解】组合图形的面积=正方形的面积+三角形的面积=边长×边长+底×高÷2,代入对应的数字即可得出答案.
4.1300公顷;13平方千米
【详解】50米=0.05千米
260×0.05=13(km )
13×100=1300(公顷)
5.(1)40.5dm2 (2)16.2元
【详解】(1)30×50-30×10÷2=1350(cm2)=13.5(dm2) 13.5×3=40.5(dm2)
(2)40.5dm2=0.405(m2) 0.405×40=16.2(元)
6.茄子:240m2 黄瓜:800m2 西红柿:608m2 0.1648公顷
【详解】茄子:240m2 黄瓜:800m2 西红柿:608m2 240+800+608=1648(m2)=0.1648(公顷)
7.420cm2
【解析】略
8.(1)13平方米
(2)58.5元
【分析】(1)根据图示可知,求组合图形的面积可以转化为一个梯形的面积和一个长方形面积的和,利用梯形面积公式:S=(a+b)h÷2,以及长方形面积公式:S=ab,计算即可。
(2)用每平方米的单价乘面积,就是总钱数,据此解答即可。
【详解】(1)(3+5)×(3-1)÷2+5×1
=8+5
=13(平方米)
答:这块钢板的面积是13平方米。
(2)13×4.5=58.5(元)
答:购买这块钢板需要58.5元。
【点睛】本题主要考查组合图形的面积,关键是把不规则图形,转化为规则图形。
9.①6.6平方米;②3平方米
【分析】①根据长方形和梯形的面积公式,先分别计算铁板上下两个部分的面积,再相加求出铁板的面积;
②用铁板的面积6.6平方米除以2.2千克,求出每千克油漆可以涂多少平方米。
【详解】①(1.2+2.8)×1.2÷2+1.5×2.8
=4×1.2÷2+4.2
=2.4+4.2
=6.6(平方米)
答:这块铁板的面积是6.6平方米。
②6.6÷2.2=3(平方米)
答:每千克油漆可以涂3平方米。
【点睛】本题考查了组合图形的面积,掌握分割法求组合图形的面积是解题的关键。
10.240千克
【分析】如图:
将指示牌分成长方形与三角形两部分,求出面积和,乘2求出正反两面的面积;再乘每平方厘米用油漆的质量,即可求出一个指示牌需要油漆的质量,最后乘50即可得解。
【详解】(30×10+20×10÷2)×2×6×50
=400×2×6×50
=800×300
=240000(克)
240000克=240千克。
答:制作50个这样的指示牌共需油漆240千克。
【点睛】本题主要考查组合图形面积的求法,解题时注意单位的变化。
11.14平方厘米
【分析】正方形面积-剪下的三角形面积=剩余部分的面积。
【详解】
4×4-2×2÷2
=16-2
=14(平方厘米)
答:剩余部分面积是14平方厘米。
【点睛】本题主要考查组合图形的面积,此类问题一般通过割补法进行解答。
12.1375平方米
【分析】用梯形面积减去平行四边形的小路面积即可。
【详解】(50+64)×25÷2-2×25
=1425-50
=1375(平方米)
答:种小麦的面积是1375平方米。
【点睛】熟悉组合图形面积的一般计算方法为本题考查重点。
13.297平方米
【分析】观察图形可得:扩建后增加的面积等于底为(43-25)米、高为33米的三角形的面积,然后再根据三角形的面积公式S=ah÷2进行解答。
【详解】(43-25)×33÷2
=18×33÷2
=297(平方米)
答:扩建后面积增加了297平方米。
【点睛】解答求组合图形的面积,关键是观察分析图形是由哪几部分组成的,是求各部分的面积和、还是求各部分的面积差,再根据相应的面积公式解答。
14.2250m2
【详解】60×34+35×12÷2=2250(m2)
15.22.5平方厘米
【详解】试题分析:由图意知:7.5厘米是2个平行四边形的高之和,这2个平行四边形的底相等,都是3厘米,所以这个图形的面积=2个平行四边形的面积之和=底×左边平行四边形的高+底×右边平行四边形的高=底×(左边平行四边形的高+右边平行四边形的高)=3×7.5.
解:3×7.5=22.5(平方厘米).
答:这个图形的面积是22.5平方厘米.
点评:解决本题的关键是由题意得出7.5厘米是2个平行四边形的高之和,这2个平行四边形的底相等,都是3厘米,再计算.
16.(1)56平方米;
(2)672元
【分析】(1)将图形分割如下:
原图形的面积=长方形的面积+梯形的面积,代入数据计算即可;
(2)用空地的面积×每平方米草皮的价格即可。
【详解】(1)8×4+(4+12-4)×(8-4)÷2
=32+12×4÷2
=32+24
=56(平方米)
答:这块空地的面积是56平方米。
(2)56×12=672(元)
答:植满这块地需要672元。
【点睛】本题主要考查求组合图形的面积,通常采用分割法。
17.10米
【分析】先求出三角形的面积,从这块地的面积里减去三角形的面积,再根据平行四边形的面积公式,求出平行四边形的高即可.
【详解】12×12÷2=72(平方米)(192-72)÷12=120÷12=10(米)
答:这块平行四边形菜地的高是10米.
18.2400平方米
【分析】由图可知,阴影部分三角形的高和梯形的高相等,根据百合花的种植面积求出梯形的高,最后利用“梯形的面积=(上底+下底)×高÷2”求出这个梯形苗圃的面积。
【详解】梯形的高:1500×2÷40
=3000÷40
=75(米)
面积:(24+40)×75÷2
=64×75÷2
=4800÷2
=2400(平方米)
答:这个梯形苗圃的面积是2400平方米。
【点睛】利用三角形的面积求出梯形的高是解答题目的关键。
19.4.4平方米;2.2千克
【详解】4×2.2=8.8(平方米)
8.8÷2=4.4(平方米)
8.8×0.25
=2.2×(4×0.25)
=2.2×1
=2.2(千克)
答:种白菜的面积是4.4平方米,共需施肥2.2千克。
【点睛】本题考查了三角形面积公式的应用和乘法的意义。
20.166平方米
【分析】观察图形可知,草地的面积=长方形的面积-正方形的面积-梯形的面积,根据长方形的面积=长×宽,正方形的面积=边长×边长,梯形的面积=(上底+下底)×高÷2,代入数据计算即可。
【详解】长方形的面积:
20×10=200(平方米)
正方形的面积:
4×4=16(平方米)
梯形的面积:
(5+7)×3÷2
=12×3÷2
=18(平方米)
草地的面积:
200-16-18=166(平方米)
答:草地的面积是166平方米。
【点睛】本题考查组合图形面积的求法,先分析出组合图形是由哪些图形相加或相减得到,然后根据图形面积公式列式计算。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
