必修1第3章3.1.1方程的根与函数的零点
文档属性
| 名称 | 必修1第3章3.1.1方程的根与函数的零点 |  | |
| 格式 | rar | ||
| 文件大小 | 145.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-23 16:12:00 | ||
图片预览





文档简介
课件17张PPT。3.1 函数与方程课题:3.1.1 方程的根与函数的零点教学目标:1.熟练掌握二次函数的图象,会判断一元二次方程根的存在性及根的个数。
2.了解函数的零点与方程根的联系。
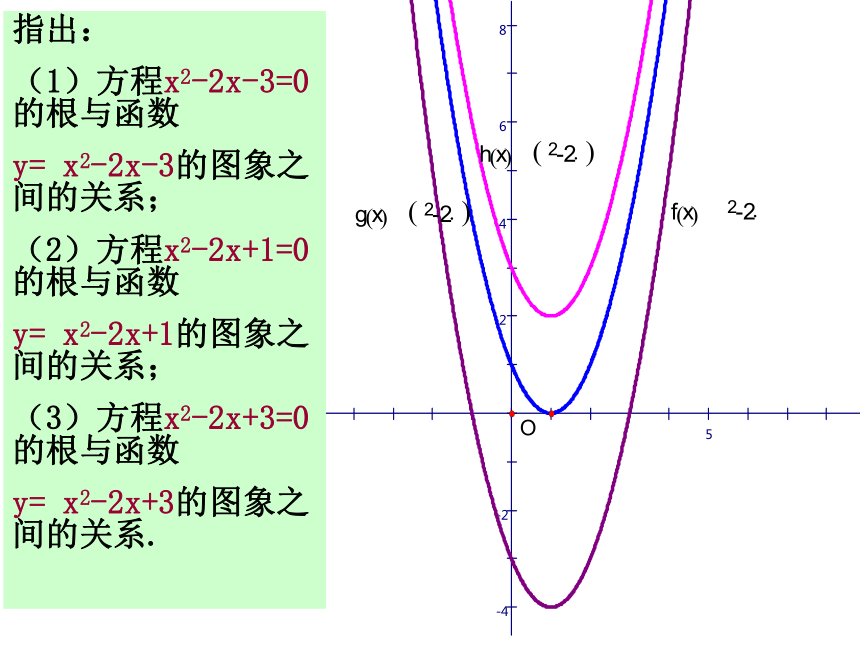
3.认识到函数的图象及单调性在确定零点的作用。提出问题:一元二次方程 的根与二次函数 的图象有什么关系?先来观察几个具体的一元二次方程及其相应的二次函数的图象:O指出:
(1)方程x2-2x-3=0的根与函数
y= x2-2x-3的图象之间的关系;
(2)方程x2-2x+1=0的根与函数
y= x2-2x+1的图象之间的关系;
(3)方程x2-2x+3=0的根与函数
y= x2-2x+3的图象之间的关系.
有两个不等的
实数根x1,x2
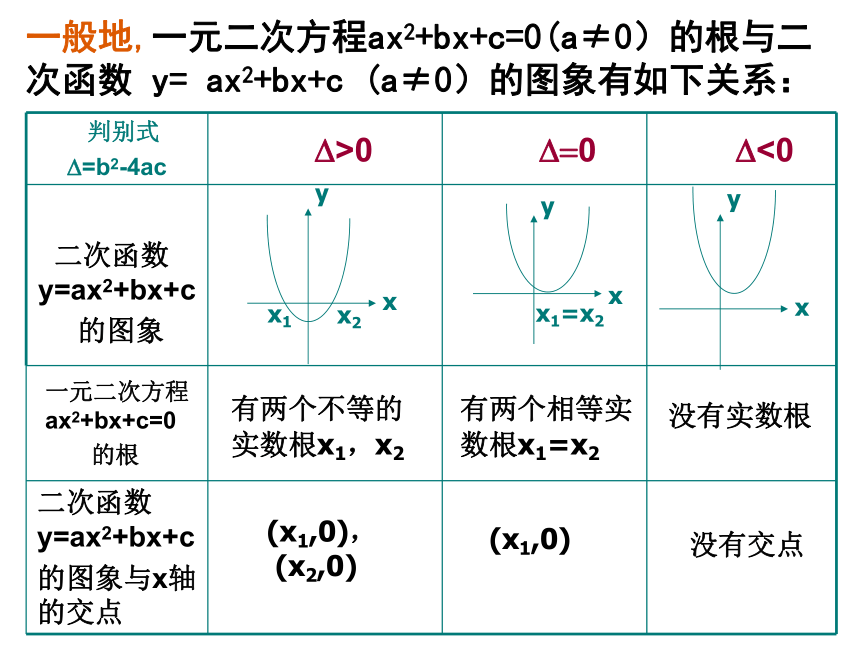
有两个相等实数根x1=x2没有实数根一般地,一元二次方程ax2+bx+c=0(a≠0)的根与二次函数 y= ax2+bx+c (a≠0)的图象有如下关系:(x1,0),
(x2,0) (x1,0)没有交点结论:一元二次方程的根与相应的二次函数图象的关系是推广到一般情形是:函数y=f(x)的图象与x轴的交点情况方程f(x)=0的实根情况若一元二次方程有实数根,它的根就是相应二次函数的图象与x轴交点的横坐标;
若一元二次方程没有实数根,则相应二次函数的图象与x轴没有交点.想一想:推广到一般情形又怎样呢? 定义:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点(zero point).方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点引出函数零点的概念剖析概念,你能得出什么结论吗?结论:函数y=f(x)的零点就是方程f(x)=0的实数根。想一想,怎样求函数的零点呢?求函数的零点有两种方法:
①代数法:求方程f(x)=0的实数根;
②几何法:将它与函数y=f(x)的图象联系起来,并利用函数的性质找出零点。下面我们来探究二次函数的零点情况1、用代数法探究结论:二次函数(1)△>0,二次函数有两个零点;(2)△=0,二次函数有一个二重零点或二阶零点;(3)△<0,二次函数没有零点。2、用数形结合法探究(以 为例)观察二次函数 的图象,填空:①在区间[-2,1]上有零点 ;
f(-2)= ;f(1)= ;
f(-2)·f(1) 0。②在区间[2,4]上有零点 ;
f(2)·f(4) 0。-15- 4<3<想一想:怎样判断一个函数在给定区间上是否存在零点呢?让我们来看一个例子观察下面函数y=f(x)的图象·
·
·
·
adcb①在区间[a,b]上 (有/无
零点;f(a)·f(b) 0.②在区间[b,c]上 (有/无零点);
f(b)·f(c) 0.③在区间[c,d]上 (有/无零点);f(b)·f(c) 0.有有有<<< ?你知道判断一个函数在给定区间上是否存在零点的方法了吗? 如果函数y=f(x)在区间[a,b]上的图象是连续不断一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点.即存在c∈(a,b),使得f(c )=0,这个c也就是方程f(x)=0的根.结论连续函数在某个区间上存在零点的判别方法:思考:若函数y=f(x)在区间[a,b]上有零点,是否一定有f(a)·f(b)<0?例1 求函数f(x)=lnx+2x-6的零点个数.解:用计算器或计算机作出x、f(x)的对应值表(表3--1)和图象(图3.1--3). x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972 表3--1分析:先说明它存在零点,再求零点的个数。巩固深化图3.1--3 由表3--1和图3.1--3可知,f(2)<0,f(3)>0,即f(2)· f(3) <0,说明这个函数在区间(2,3)内有零点。
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.0 1 2 3 4例2.函数 的零点所在的大致区间是( ) A . (1, 2) B . (2, 3)C . 和(3, 4) D . (e, +∞)分析:从已知的区间(a,b) ,求f(a),f(b),判断是否有f(a)·f(b)<0.解:因为f(1)=-2<0,f(2)=ln2-1<0,故在(1,2)内没有零点,非A.又f(3)=ln3-2/3>0,所以f(2)·f(3)<0,所以f(x)在(2,3)内有一个零点,选B.例3. 若方程 在(0, 1)内恰有一解,求实数a的取值范围.分析:令 ,由题意应有f(0)·f(1)<0,解出a. 解:令 ,因为方程在(0,1)内恰在一解,则f(0)·f(1)<0,即
-1·(2a-2)<0,解得 a>1. 例4.二次函数 中,
a·c<0,则函数的零点个数是( ). A. 1个 B. 2个 C. 0个 D. 无法确定分析:分析条件a·c<0,a是二次项系数,确定抛物线的开口方向, c=f(0), 所以a·c=a·f(0)<0,由此可解出a. 解:因为c=f(0),所以a与f(0)异号,即: a>0f(0)<0或a<0f(0)>0所以函数必有两个零点,故选B.小结1、一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y= ax2+bx+c (a≠0)的图象的关系;
2、函数零点的概念;3、连续函数在某个区间上存在零点的判别方法。作业P92 习题3.1 第2、3题再见
2.了解函数的零点与方程根的联系。
3.认识到函数的图象及单调性在确定零点的作用。提出问题:一元二次方程 的根与二次函数 的图象有什么关系?先来观察几个具体的一元二次方程及其相应的二次函数的图象:O指出:
(1)方程x2-2x-3=0的根与函数
y= x2-2x-3的图象之间的关系;
(2)方程x2-2x+1=0的根与函数
y= x2-2x+1的图象之间的关系;
(3)方程x2-2x+3=0的根与函数
y= x2-2x+3的图象之间的关系.
有两个不等的
实数根x1,x2
有两个相等实数根x1=x2没有实数根一般地,一元二次方程ax2+bx+c=0(a≠0)的根与二次函数 y= ax2+bx+c (a≠0)的图象有如下关系:(x1,0),
(x2,0) (x1,0)没有交点结论:一元二次方程的根与相应的二次函数图象的关系是推广到一般情形是:函数y=f(x)的图象与x轴的交点情况方程f(x)=0的实根情况若一元二次方程有实数根,它的根就是相应二次函数的图象与x轴交点的横坐标;
若一元二次方程没有实数根,则相应二次函数的图象与x轴没有交点.想一想:推广到一般情形又怎样呢? 定义:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点(zero point).方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点引出函数零点的概念剖析概念,你能得出什么结论吗?结论:函数y=f(x)的零点就是方程f(x)=0的实数根。想一想,怎样求函数的零点呢?求函数的零点有两种方法:
①代数法:求方程f(x)=0的实数根;
②几何法:将它与函数y=f(x)的图象联系起来,并利用函数的性质找出零点。下面我们来探究二次函数的零点情况1、用代数法探究结论:二次函数(1)△>0,二次函数有两个零点;(2)△=0,二次函数有一个二重零点或二阶零点;(3)△<0,二次函数没有零点。2、用数形结合法探究(以 为例)观察二次函数 的图象,填空:①在区间[-2,1]上有零点 ;
f(-2)= ;f(1)= ;
f(-2)·f(1) 0。②在区间[2,4]上有零点 ;
f(2)·f(4) 0。-15- 4<3<想一想:怎样判断一个函数在给定区间上是否存在零点呢?让我们来看一个例子观察下面函数y=f(x)的图象·
·
·
·
adcb①在区间[a,b]上 (有/无
零点;f(a)·f(b) 0.②在区间[b,c]上 (有/无零点);
f(b)·f(c) 0.③在区间[c,d]上 (有/无零点);f(b)·f(c) 0.有有有<<< ?你知道判断一个函数在给定区间上是否存在零点的方法了吗? 如果函数y=f(x)在区间[a,b]上的图象是连续不断一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点.即存在c∈(a,b),使得f(c )=0,这个c也就是方程f(x)=0的根.结论连续函数在某个区间上存在零点的判别方法:思考:若函数y=f(x)在区间[a,b]上有零点,是否一定有f(a)·f(b)<0?例1 求函数f(x)=lnx+2x-6的零点个数.解:用计算器或计算机作出x、f(x)的对应值表(表3--1)和图象(图3.1--3). x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972 表3--1分析:先说明它存在零点,再求零点的个数。巩固深化图3.1--3 由表3--1和图3.1--3可知,f(2)<0,f(3)>0,即f(2)· f(3) <0,说明这个函数在区间(2,3)内有零点。
由于函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点.0 1 2 3 4例2.函数 的零点所在的大致区间是( ) A . (1, 2) B . (2, 3)C . 和(3, 4) D . (e, +∞)分析:从已知的区间(a,b) ,求f(a),f(b),判断是否有f(a)·f(b)<0.解:因为f(1)=-2<0,f(2)=ln2-1<0,故在(1,2)内没有零点,非A.又f(3)=ln3-2/3>0,所以f(2)·f(3)<0,所以f(x)在(2,3)内有一个零点,选B.例3. 若方程 在(0, 1)内恰有一解,求实数a的取值范围.分析:令 ,由题意应有f(0)·f(1)<0,解出a. 解:令 ,因为方程在(0,1)内恰在一解,则f(0)·f(1)<0,即
-1·(2a-2)<0,解得 a>1. 例4.二次函数 中,
a·c<0,则函数的零点个数是( ). A. 1个 B. 2个 C. 0个 D. 无法确定分析:分析条件a·c<0,a是二次项系数,确定抛物线的开口方向, c=f(0), 所以a·c=a·f(0)<0,由此可解出a. 解:因为c=f(0),所以a与f(0)异号,即: a>0f(0)<0或a<0f(0)>0所以函数必有两个零点,故选B.小结1、一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y= ax2+bx+c (a≠0)的图象的关系;
2、函数零点的概念;3、连续函数在某个区间上存在零点的判别方法。作业P92 习题3.1 第2、3题再见
