第24章 圆 全章综合检测（含答案）

第24章 圆 全章综合检测
(限时:90分钟 满 分:120分)
一、选择题(每小题3分，共30分)
1 已知⊙O 的直径是 4 cm,OP=4 cm,则点 P ( )
A.在⊙O外 B.在⊙O上
C.在⊙O内 D.不能确定
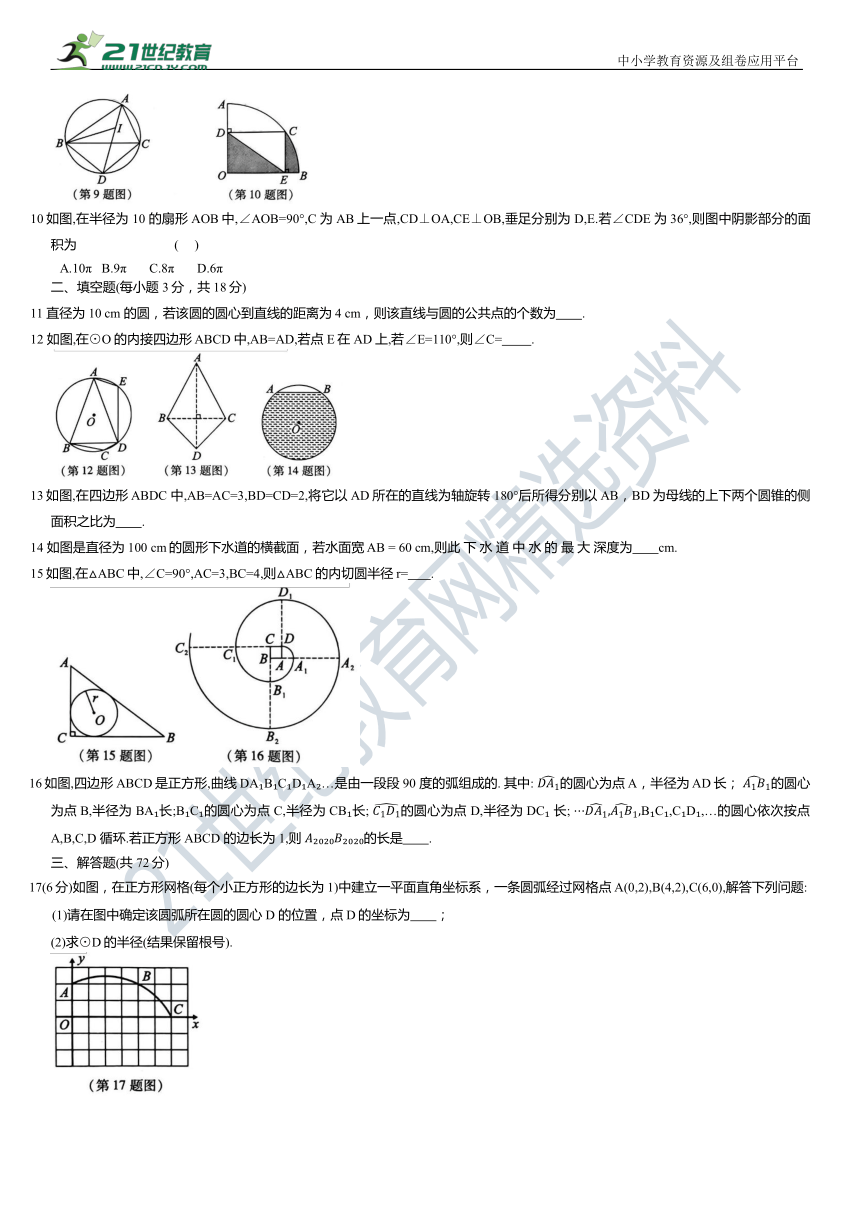
2 下列结论正确的是 ( )
A.三点确定一个圆
B.相等的圆心角所对的弧相等
C.等弧所对的弦相等
D.三角形的外心到三角形各边的距离相等
3如图,点 A,B,C 在⊙O 上,∠ACB=54°,则∠ABO的度数是 ( )
A.54° B.27°
C.36° D.108°
4 已知在 Rt△ABC中,∠C=90°,AC=8,BC=6,以点 C为圆心,5 为半径的圆与直线 AB 的位置关系是 ( )
A.相切 B.相交 C.相离 D.无法确定
5如图,PA,PB 为圆O 的切线,切点分别为A,B,PO 交AB 于点 C,PO的延长线交圆O于点 D.下列结论不一定成立的是 ( )
A.△BPA为等腰三角形
B. AB 与PD相互垂直平分
C.点A，B都在以 PO长为直径的圆上
D. PC为△BPA 的边 AB上的中线
6 如图,在⊙O中,AB,AC 是互相垂直的两条弦,OD⊥AB于点 D,OE⊥AC于点E,且AB=8cm ,AC=6cm,那么⊙O的半径OA长为 ( )
A.4 cm B.5cm C.6 cm D. 8cm
7 如图,△ABC是⊙O 的内接三角形,∠A=119°,过点 C的圆的切线交 BO 于点P，则∠P 的度数为 ( )
A.32° B.31° C.29° D.61°
8 如图，螺母的一个面ABCDEF可以看作是正六边形，这个正六边形 ABCDEF 的外接圆的半径是 2√ cm,则这个正六边形的周长是 ( )
A.12 cm
C.36 cm
9 如图,已知△ABC的外接圆,I是△ABC的内心,AI 的延长线与圆相交于点 D，连接 BI，BD，DC.则下列说法错误的是 ( )
A.线段 DB 绕点 D 顺时针旋转一定能与线段 DC 重合
B.线段 DB 绕点 D 顺时针旋转一定能与线段 DI重合
C.∠ABI绕点 B顺时针旋转一定能与∠IBC重合
D.线段 CD 绕点 C 顺时针旋转一定能与线段 CA 重合
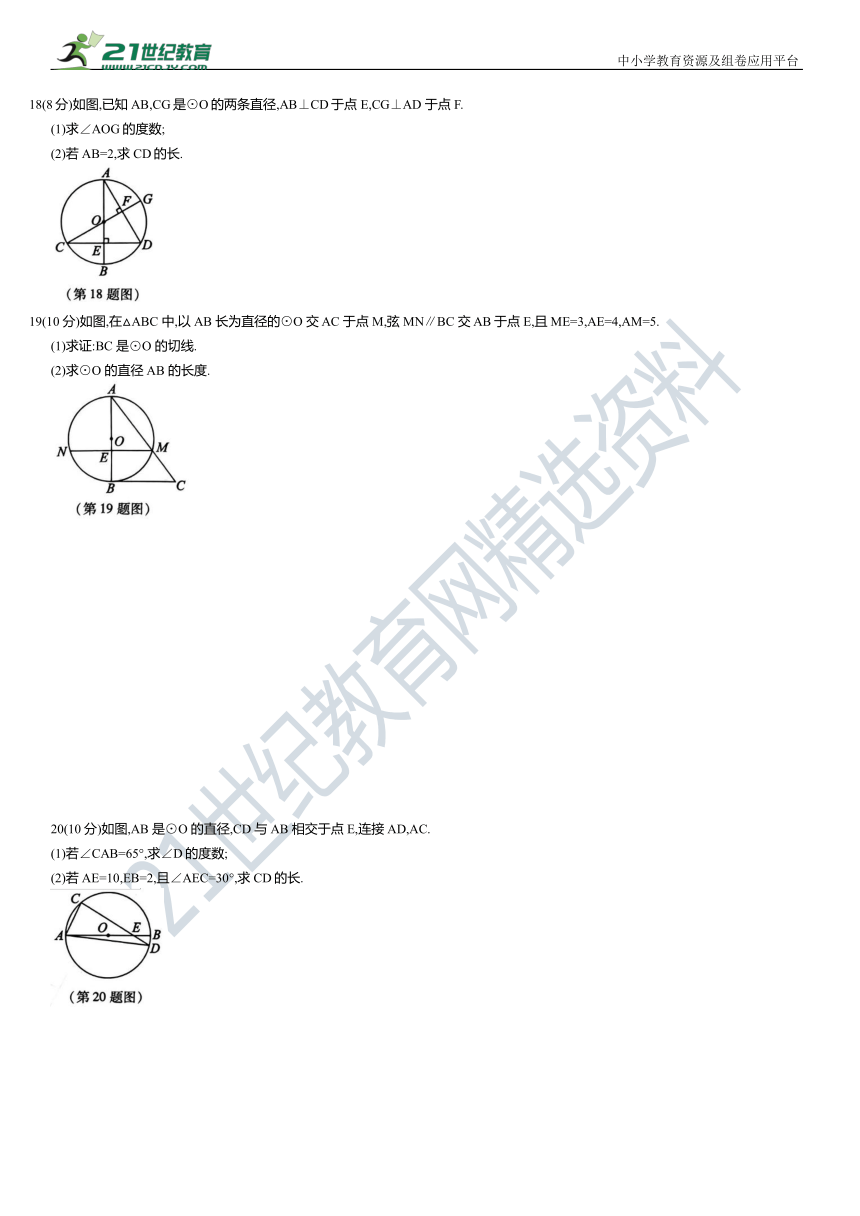
10如图,在半径为 10 的扇形AOB中,∠AOB=90°,C 为AB上一点,CD⊥OA,CE⊥OB,垂足分别为 D,E.若∠CDE 为36°,则图中阴影部分的面积为 ( )
A.10π B.9π C.8π D.6π
二、填空题(每小题3分，共18分)
11 直径为 10 cm 的圆，若该圆的圆心到直线的距离为4 cm，则该直线与圆的公共点的个数为 .
12 如图,在⊙O的内接四边形 ABCD 中,AB=AD,若点 E在AD上,若∠E=110°,则∠C= .
13如图,在四边形 ABDC 中,AB=AC=3,BD=CD=2,将它以AD所在的直线为轴旋转180°后所得分别以AB，BD为母线的上下两个圆锥的侧面积之比为 .
14 如图是直径为 100 cm的圆形下水道的横截面，若水面宽 AB = 60 cm,则此 下 水 道 中 水 的 最 大 深度为 cm.
15如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r= .
16如图,四边形ABCD是正方形,曲线DA B C D A …是由一段段90 度的弧组成的. 其中: 的圆心为点 A，半径为 AD长； 的圆心为点B,半径为 BA 长;B C 的圆心为点 C,半径为 CB 长; 的圆心为点 D,半径为 DC 长; B C ,C D ,…的圆心依次按点 A,B,C,D 循环.若正方形ABCD 的边长为1,则 的长是 .
三、解答题(共72分)
17(6分)如图，在正方形网格(每个小正方形的边长为1)中建立一平面直角坐标系，一条圆弧经过网格点A(0,2),B(4,2),C(6,0),解答下列问题:
(1)请在图中确定该圆弧所在圆的圆心 D 的位置，点D的坐标为 ；
(2)求⊙D的半径(结果保留根号).
18(8分)如图,已知AB,CG是⊙O的两条直径,AB⊥CD于点 E,CG⊥AD 于点 F.
(1)求∠AOG的度数;
(2)若AB=2,求 CD的长.
19(10 分)如图,在△ABC 中,以AB 长为直径的⊙O 交 AC 于点 M,弦 MN∥BC 交 AB于点 E,且ME=3,AE=4,AM=5.
(1)求证:BC 是⊙O 的切线.
(2)求⊙O 的直径AB 的长度.
20(10 分)如图,AB 是⊙O 的直径,CD 与AB 相交于点E,连接AD,AC.
(1)若∠CAB=65°,求∠D的度数;
(2)若AE=10,EB=2,且∠AEC=30°,求 CD的长.
中小学教育资源及组卷应用平台
21 (12 分)已知 PA,PB 分别与⊙O 相切于点 A,B,∠APB=80°,C为⊙O 上一点.
(1)如图(1),求∠ACB 的大小.
(2)如图(2),AE 为⊙O 的直径,AE 与 BC 相交于点
D.若AB=AD,求∠EAC 的大小.
22(12 分)如图,△ABC 是等腰三角形,且 AC=BC,∠ACB=120°,在AB上取一点 O,使 OB=OC,以O为圆心,OB为半径作⊙O,过点 C 作 CD∥AB 交⊙O 于点 D,连接 BD.
(1)猜想AC与⊙O 的位置关系，并证明你的猜想；
(2)试判断四边形 BOCD 的形状，并证明你的结论；
(3)已知AC=6，求扇形 OBC 围成的圆锥的底面圆的半径.
23 (14 分)如图,在△ABC 中,AD 是 BC 边上的中线, ,CE 交 BA 的延长线于点 E,
(1)求 CE 的长.
(2)求证:△ABC为等腰三角形.
(3)求△ABC 的外接圆的圆心 P 与内切圆的圆心 Q之间的距离.
全章综合检测
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C B B B A D D A
二、11.2
12.140° 解析由题图知,四边形 ABDE 是⊙O 的内接四边形,∴∠ABD=180°-∠E=70°. ∵ AB =AD,∴ ∠ADB =∠ABD=70°, ∵四边形ABCD是⊙O的内接四边形,∴
13.3：2 解析∵ 两个圆锥的底面圆相同，∴ 可设底面圆的周长为c，∴上面圆锥的侧面积为 ，下面圆锥的侧面积为 c.BD.∵AB=AC=3,BD=CD=2,∴S上:SF=3:2.
14.90 解析如答图,连接 OA,过点 O 作 MN⊥AB,垂足为 N ∵水管的直径是 100 cm,∴ OA = 50cm,∴ 在Rt△AON中,由勾股定理,得 40(cm),∴MN=OM+ON=90(cm).∴此下水道中水的最大深度为90 cm.
15.1 解析在 △ABC 中,∠C=90°,AC=3,BC=4,根据勾股定理,得 AB=5.如答图，设△ABC的内切圆与三条边的切点分别为 D,E,F,连接 OD,OE,OF,∴OD⊥AB,OE⊥BC,OF⊥AC.∵∠C=90°,∴ 四边形 EOFC 是矩形.根据切线长定理，得CE=CF,∴矩形EOFC 是正方形,∴CE=CF=r,∴AF=AD=AC-FC=3-r,BE=BD=BC-CE=4-r. ∵AD+BD=AB,∴3-r+4-r=5,解得r=1.故△ABC的内切圆半径r=1.
16.4039π 解析由题图可知,曲线DA B C D A …是由一段段90度的弧组成的，半径每次为前一段弧的半径+1，即 BB =2,…,AD =AA =4(n-1)+1,BA =BB =4(n-1)+2. 的半径为 的弧长为
三、17.解(1)如答图. (2分)
(2,-2). (3分)
(2)如答图,过点D作DE⊥y轴于点E,连接AD. (4分)
∵在 Rt△ADE 中,AE=4,DE=2,
即⊙D的半径为2 ………………(6分)
18.解(1)如答图,连接OD. (1分)
∵AB⊥CD,
∴BC=BD,∴∠BOC=∠BOD. (2分)
由圆周角定理，得 …… (3分)
∵∠AOG=∠BOC,∴∠AOG=∠BOD,∴∠A= ∠AOG.
∵∠OFA=90°,∴∠AOG=60°. (4分)
(2)∵∠AOG=60°,∴∠COE=60°.
∵∠OEC=90°,∴∠C=30°, (6分)
(7分)
∵AB⊥CD,∴CD=2CE= . (8分)
9.(1)证明∵在△AME 中,ME=3,AE=4,AM=5,
∴△AME是直角三角形,且∠AEM=90°. (2分)
又∵MN∥BC,
∴∠ABC=∠AEM=90°,
∴AB⊥BC. (3分)
∵AB为⊙O 的直径,
∴BC是⊙O的切线. …………… . . . . .(5分)
(2)解如答图,连接OM.设⊙O的半径是r.
在Rt△OEM中,∵OE=AE-OA=4-r,ME=3,OM=r, (7 分)
解得 (8分)
(10 分)
20.解(1)如答图,连接 BC.∵AB是⊙O 的直径,∴∠ACB=90°. ……(2分)
∴∠D=∠B=25°. (5分)
(2)如答图,连接OC,过点 O 作 OF⊥CD,垂足为 F.
∵AE=10,BE=2,∴OC=OA=6,OE=6-2=4. (8分)
∵∠AEC=30°,∴在 Rt△OFE中,OF=2,
∵在 Rt△OFC 中,由勾股定理,得
解得 CD=2CF=8 . (10分)(负值已舍去),∴(
21.解(1)如答图(1),连接OA,OB. (1分)
∵PA,PB是⊙O的切线,∴∠OAP=∠OBP=90°,…………(3分)
…………………………(4分)
由圆周角定理，得 ……………………(5分)
(2)如答图(2),连接CE. (6分)
∵AE为⊙O的直径,∴∠ACE=90°, (8分)
(10 分)
∴∠EAC=∠ADB-∠ACB=70°-50°=20°, (12 分)
22.解(1)AC与⊙O 相切.证明如下:
∵AC=BC,∠ACB=120°,∴∠A=∠ABC=30°. (2分)
∵OB=OC,∴∠OCB=∠OBC=30°,
∴∠ACO=∠ACB-∠OCB=90°,
∴OC⊥AC. (3分)
∵OC 是⊙O 的半径,
∴AC 是⊙O 的切线.
∴AC与⊙O相切. (4分)
(2)四边形 BOCD 为菱形.证明如下: ……………………………………(5分)
如答图，连接OD.
∵CD∥AB,∴∠AOC=∠OCD.
∵∠AOC=∠OBC+∠OCB=60°,∴∠OCD=60°. (6分)
∵OC=OD,∴△OCD为等边三角形,
∴CD=OB=OC, (7分)
∴四边形BOCD为菱形. (8分)
(3)在 Rt△AOC中,∵AC=6,∠A=30°,
的长为 ……(10 分)
设扇形OBC围成的圆锥的底面圆的半径为r，则 ………………………………………(12分)
23.(1)据∵AD 是边 BC上的中线,∴BD=CD.……………………………………………(2分)
∵CE∥AD,∴AD为△BCE 的中位线,
∴CE=2AD=6. (4分)
(2)证明∵CE∥AD,∴∠BAD=∠E,∠CAD=∠ACE.…………………………(6分)
∵∠BAD=∠CAD,∴∠ACE=∠E,∴AE=AC.由(1)得AD为△BCE的中位线,
∴AB=AE,∴AB=AC,
∴△ABC为等腰三角形. (8分)
(3)解如答图,连接BP,BQ,CQ,作△ABC的外接圆⊙P,△ABC的内切圆⊙Q.
在 Rt△ABD中,由勾股定理,得 …(10分)
设⊙P的半径为 R,⊙Q的半径为r,则PD=R-3.
在 Rt△PBD中, 即 解得
……………………………………(11分)
解得 即 …(13分)
故△ABC的外接圆的圆心 P 与内切圆的圆心Q之间的距离为 .
…………………………………………………………………(14分)