2024鲁教版数学七年级下册--第八章《平行线的有关证明》素养综合检测(含解析)
文档属性
| 名称 | 2024鲁教版数学七年级下册--第八章《平行线的有关证明》素养综合检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 484.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:44 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024鲁教版数学七年级下册
第八章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
1.下列语句中命题的个数是( )
①两点之间线段最短;
②连接P,Q两点;
③不相交的两条直线平行;
④对顶角的平分线在同一条直线上;
⑤两个有理数相加,和一定大于每一个加数吗
A.2 B.3 C.4 D.5
2.下列说法中,是定义的是( )
A.对顶角相等
B.三角形的三个内角和等于180°
C.三角形一边上的中线把三角形的面积二等分
D.只含有一个未知数,且未知数的最高次数是1的整式方程叫一元一次方程
3.(2023安徽六安金安期末)对于命题“如果∠1+∠2=90°,那么∠1≠
∠2”,能说明它是假命题的反例是( )
A.∠1=∠2=45°
B.∠1=50°,∠2=50°
C.∠1=50°,∠2=40°
D.∠1=40°,∠2=40°
4.给出下列命题:(1)三角形的一个外角一定大于它的一个内角;(2)若一个三角形的三个内角的度数之比为1∶3∶4,则它肯定是直角三角形;(3)三角形的最小内角不能大于60°;(4)三角形的一个外角等于和它不相邻的两个内角的和.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
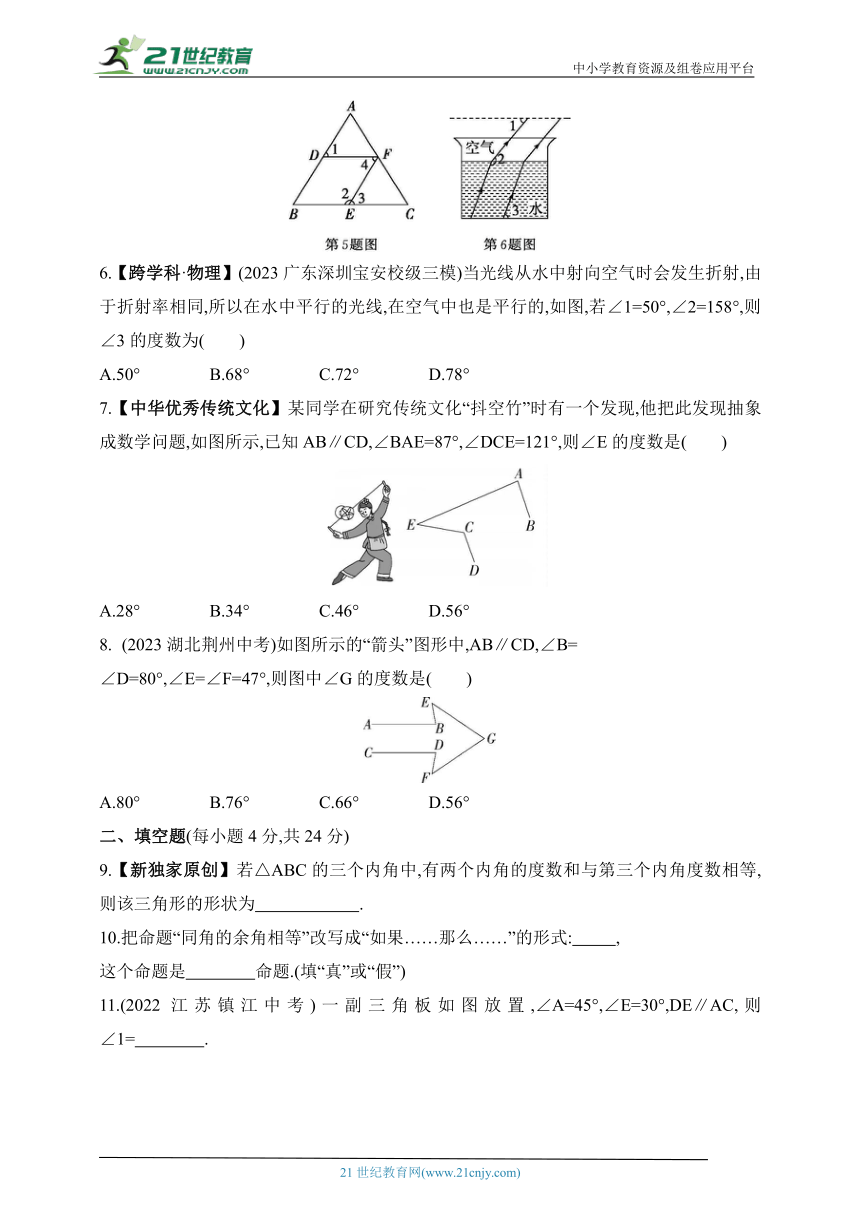
5.(2023浙江温州月考)如图,在下列给出的条件中,能判定EF∥AB的是( )
A.∠4=∠3 B.∠1=∠4
C.∠1=∠B D.∠4+∠2=180°
6.【跨学科·物理】(2023广东深圳宝安校级三模)当光线从水中射向空气时会发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的,如图,若∠1=50°,∠2=158°,则∠3的度数为( )
A.50° B.68° C.72° D.78°
7.【中华优秀传统文化】某同学在研究传统文化“抖空竹”时有一个发现,他把此发现抽象成数学问题,如图所示,已知AB∥CD,∠BAE=87°,∠DCE=121°,则∠E的度数是( )
A.28° B.34° C.46° D.56°
(2023湖北荆州中考)如图所示的“箭头”图形中,AB∥CD,∠B=
∠D=80°,∠E=∠F=47°,则图中∠G的度数是( )
A.80° B.76° C.66° D.56°
二、填空题(每小题4分,共24分)
9.【新独家原创】若△ABC的三个内角中,有两个内角的度数和与第三个内角度数相等,则该三角形的形状为 .
10.把命题“同角的余角相等”改写成“如果……那么……”的形式: ,
这个命题是 命题.(填“真”或“假”)
11.(2022江苏镇江中考)一副三角板如图放置,∠A=45°,∠E=30°,DE∥AC,则∠1= .
如图,一条公路修到湖边时,需拐弯绕湖而过,若∠A=130°,
∠B=150°,AF∥CD,则∠C的度数为 .
(2022吉林长春南关期末)如图,已知BC⊥AE,DE⊥AE,∠2+
∠3=180°.若∠1=66°,BC平分∠ABD,则∠ACF= °.
14.(2023广东中山期末改编)如图,∠A+∠B+∠C+∠D+∠E的度数为 .
三、解答题(共44分)
15.(8分)阅读材料并解决问题:
一些命题的正确性需要经过推理才能作出判断,这个推理过程叫做证明,证明中的每一步推理都要有依据,这些依据可以是已知条件,也可以是学过的定义、基本事实、定理等,而判断一个命题是假命题,只需要举出一个例子(反例),使它符合命题的条件,但不满足结论即可.
(1)把命题“在同一平面内,垂直于同一条直线的两条直线平行”写成“如果……那么……”的形式.
(2)判断(1)中的命题是不是真命题,如果是,请写出证明过程;如果不是,请举出反例.
(要求:画出相应的图形,并用文字语言或符号语言进行表述)
16.(2023山东济宁金乡月考)(8分)如图,现有以下3个论断:①AB∥CD;②∠B=∠C;③∠E=∠F.请以其中2个论断为条件,另一个论断为结论构造命题.
(1)你构造的是哪几个命题
(2)请选择其中一个真命题加以证明.
17.(2023山东济南莱芜期中)(8分)如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
18.(8分)如图,BD∥GE,∠AFG=∠1=50°.
(1)求证:AF∥DE;
(2)若AQ平分∠FAC,交BD的延长线于点Q,且∠Q=15°,求∠ACQ的度数.
19.(2022山东泰安新泰期中)(12分)在△ABC中,AE平分∠BAC,∠C>∠B.
(1)如图1,若AD⊥BC于点D,∠B=40°,∠C=60°,求∠EAD的度数;
(2)如图1,根据(1)的解答过程,猜想∠B、∠C、∠EAD之间的数量关系,并说明理由;
(3)如图2,在线段AE上任取一点P(不与点A、E重合),过点P作PD⊥BC于点D,请写出∠B、∠C、∠EPD之间的数量关系,并说明理由.
答案全解全析
1.B 命题有①两点之间线段最短;③不相交的两条直线平行;④对顶角的平分线在同一条直线上.②⑤不是判断,不是命题.故选B.
2.D A,B,C都是性质,D是一元一次方程的定义.故选D.
3.A A项,满足条件,不满足结论,故A选项符合题意;B项,不满足条件,也不满足结论,故B选项不符合题意;C项,满足条件∠1+∠2=90°,也满足结论∠1≠∠2,故C选项不符合题意;D项,不满足条件,也不满足结论,故D选项不符合题意.故选A.
4.C (1)三角形的一个外角不一定大于它的一个内角,故原命题是假命题;
(2)若一个三角形的三个内角的度数之比为1∶3∶4,则三个内角的度数分别为22.5°,67.5°,90°,故这个三角形肯定是直角三角形,故原命题是真命题;
(3)三角形的最小内角不能大于60°,是真命题;
(4)三角形的一个外角等于和它不相邻的两个内角的和,是真命题.
综上,(2)(3)(4)是真命题,共3个,故选C.
5.B A项,∵∠4=∠3,∴DF∥BC,故A不符合题意;
B项,∵∠1=∠4,∴EF∥AB,故B符合题意;
C项,∵∠1=∠B,∴DF∥BC,故C不符合题意;
D项,∵∠4+∠2=180°,∴DF∥BC,故D不符合题意.故选B.
6.C 如图所示,
根据题意可知,AC∥DE∥FG,BD∥CE,DF∥EG,
∵BC∥DE,∴∠1=∠BDE=50°,∴∠EDF=∠2-∠BDE=158°-50°=108°,∵DE∥FG,∴∠DFG=180°-∠EDF=180°-108°=72°,
∵DF∥EG,∴∠3=∠DFG=72°,故选C.
7.B 如图,延长DC交AE于F,
∵AB∥CD,∠BAE=87°,
∴∠CFE=87°,
又∵∠DCE=121°,∴∠E=∠DCE-∠CFE=121°-87°=34°,故选B.
8.C 如图,延长AB交EG于M,延长CD交FG于N,过G作GK∥AB,
∵AB∥CD,∴GK∥CD∥AB,∴∠KGM=∠EMB,∠KGN=∠DNF,
∴∠KGM+∠KGN=∠EMB+∠DNF,∴∠EGF=∠EMB+∠DNF,
∵∠ABE=80°,∠E=47°,∴∠EMB=∠ABE-∠E=33°,同理可得
∠DNF=33°,∴∠EGF=∠EMB+∠DNF=33°+33°=66°.故选C.
9.答案 直角三角形
解析 设三角形的第三个内角度数为x,则另两个内角的度数和为x,由三角形内角和为180°,可得2x=180°,所以x=90°,所以该三角形为直角三角形.
10.答案 如果两个角是同一个角的余角,那么这两个角相等;真
解析 根据命题的特点,可以改写为“如果两个角是同一个角的余角,那么这两个角相等”,这个命题为真命题.
11.答案 105°
解析 如图,设DE交AB于O点,
∵DE∥AC,∴∠DOA=∠A=45°,
∵∠D=90°-∠E=90°-30°=60°,
∴∠1=∠D+∠DOA=60°+45°=105°.
12.答案 160°
解析 如图,延长AB,交DC的延长线于点E,
由题意得,AF∥DE,∴∠A=∠E=130°,
∵∠ABC=150°,∴∠CBE=30°,
∴∠BCD=∠CBE+∠E=30°+130°=160°.
13.答案 57
解析 ∵BC⊥AE,DE⊥AE,∴BC∥DE,∴∠3+∠CBD=180°,
又∵∠2+∠3=180°,∴∠2=∠CBD,∴CF∥DB,∴∠ABD=∠1=66°,
又∵BC平分∠ABD,∴∠DBC=∠ABD=33°,∴∠2=∠DBC=33°,
又∵BC⊥AG,∴∠ACF=90°-∠2=90°-33°=57°,故答案为57.
14.答案 180°
解析 如图,
∵∠1=∠2+∠C,∠2=∠A+∠D,
∴∠1=∠A+∠C+∠D,
∵∠1+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
15.解析 (1)在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行.
(2)是真命题.
已知:如图,AB⊥EF,垂足为B,CD⊥EF,垂足为D,
求证:AB∥CD.
证明:∵AB⊥EF,CD⊥EF,
∴∠ABD=∠CDF=90°,∴AB∥CD.
16.解析 (1)由①②得③;由①③得②;由②③得①.
(2)答案不唯一.
可选择由①②得③,证明过程如下:
∵AB∥CD,∴∠EAB=∠C,
又∵∠B=∠C,∴∠EAB=∠B,∴CE∥BF,∴∠E=∠F.
17.解析 (1)证明:∵DE∥BC,∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,∴AB∥EF,
∴∠B=∠EFC,∴∠ADE=∠EFC.
(2)∵∠ACB=72°,∠A=60°,
∴∠B=180°-∠A-∠ACB=48°,
∵CD⊥AB,∴∠BDC=90°,
∴∠DCB=180°-90°-48°=42°.
18.解析 (1)证明:∵BD∥GE,∴∠E=∠1=50°,
∵∠AFG=∠1=50°,∴∠E=∠AFG,∴AF∥DE.
(2)∵∠1=50°,∠Q=15°,∴∠AHD=65°,
∵AF∥DE,∴∠FAQ=∠AHD=65°,
∵AQ平分∠FAC,∴∠CAQ=∠FAQ=65°,
∴∠ACQ=180°-∠CAQ-∠Q=180°-65°-15°=100°.
19.解析 (1)∵∠B=40°,∠C=60°,
∴∠BAC=180°-(∠B+∠C)=80°,
∵AE平分∠BAC,
∴∠EAC=∠BAC=×80°=40°,
∵AD⊥BC,∴∠ADC=90°,
∵∠C=60°,∴∠DAC=180°-90°-60°=30°,
∴∠EAD=∠EAC-∠DAC=40°-30°=10°.
(2)∠EAD=(∠C-∠B).
理由:∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-(∠B+∠C),
∵AE平分∠BAC,
∴∠CAE=∠BAC=[180°-(∠B+∠C)]=90°-(∠B+∠C),
∵AD⊥BC,∴∠ADC=90°,∴∠CAD=90°-∠C,
∴∠EAD=∠CAE-∠CAD=90°-(∠B+∠C)-(90°-∠C)=(∠C-∠B),即∠EAD=(∠C-∠B).
(3)∠EPD=∠C-∠B.
理由:如图,过A作AG⊥BC于G,
∵PD⊥BC,∴AG∥PD,∴∠GAE=∠EPD,
∵∠BAC=180°-(∠B+∠C),AE平分∠BAC,
∴∠EAC=∠BAC=[180°-(∠B+∠C)]=90°-∠B-∠C,
∵AG⊥BC,∴∠AGC=90°,
∴∠GAC=90°-∠C,
∴∠GAE=∠CAE-∠CAG=90°-∠B-∠C-(90°-∠C)=∠C-∠B,
∴∠EPD=∠C-∠B.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版数学七年级下册
第八章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
1.下列语句中命题的个数是( )
①两点之间线段最短;
②连接P,Q两点;
③不相交的两条直线平行;
④对顶角的平分线在同一条直线上;
⑤两个有理数相加,和一定大于每一个加数吗
A.2 B.3 C.4 D.5
2.下列说法中,是定义的是( )
A.对顶角相等
B.三角形的三个内角和等于180°
C.三角形一边上的中线把三角形的面积二等分
D.只含有一个未知数,且未知数的最高次数是1的整式方程叫一元一次方程
3.(2023安徽六安金安期末)对于命题“如果∠1+∠2=90°,那么∠1≠
∠2”,能说明它是假命题的反例是( )
A.∠1=∠2=45°
B.∠1=50°,∠2=50°
C.∠1=50°,∠2=40°
D.∠1=40°,∠2=40°
4.给出下列命题:(1)三角形的一个外角一定大于它的一个内角;(2)若一个三角形的三个内角的度数之比为1∶3∶4,则它肯定是直角三角形;(3)三角形的最小内角不能大于60°;(4)三角形的一个外角等于和它不相邻的两个内角的和.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
5.(2023浙江温州月考)如图,在下列给出的条件中,能判定EF∥AB的是( )
A.∠4=∠3 B.∠1=∠4
C.∠1=∠B D.∠4+∠2=180°
6.【跨学科·物理】(2023广东深圳宝安校级三模)当光线从水中射向空气时会发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的,如图,若∠1=50°,∠2=158°,则∠3的度数为( )
A.50° B.68° C.72° D.78°
7.【中华优秀传统文化】某同学在研究传统文化“抖空竹”时有一个发现,他把此发现抽象成数学问题,如图所示,已知AB∥CD,∠BAE=87°,∠DCE=121°,则∠E的度数是( )
A.28° B.34° C.46° D.56°
(2023湖北荆州中考)如图所示的“箭头”图形中,AB∥CD,∠B=
∠D=80°,∠E=∠F=47°,则图中∠G的度数是( )
A.80° B.76° C.66° D.56°
二、填空题(每小题4分,共24分)
9.【新独家原创】若△ABC的三个内角中,有两个内角的度数和与第三个内角度数相等,则该三角形的形状为 .
10.把命题“同角的余角相等”改写成“如果……那么……”的形式: ,
这个命题是 命题.(填“真”或“假”)
11.(2022江苏镇江中考)一副三角板如图放置,∠A=45°,∠E=30°,DE∥AC,则∠1= .
如图,一条公路修到湖边时,需拐弯绕湖而过,若∠A=130°,
∠B=150°,AF∥CD,则∠C的度数为 .
(2022吉林长春南关期末)如图,已知BC⊥AE,DE⊥AE,∠2+
∠3=180°.若∠1=66°,BC平分∠ABD,则∠ACF= °.
14.(2023广东中山期末改编)如图,∠A+∠B+∠C+∠D+∠E的度数为 .
三、解答题(共44分)
15.(8分)阅读材料并解决问题:
一些命题的正确性需要经过推理才能作出判断,这个推理过程叫做证明,证明中的每一步推理都要有依据,这些依据可以是已知条件,也可以是学过的定义、基本事实、定理等,而判断一个命题是假命题,只需要举出一个例子(反例),使它符合命题的条件,但不满足结论即可.
(1)把命题“在同一平面内,垂直于同一条直线的两条直线平行”写成“如果……那么……”的形式.
(2)判断(1)中的命题是不是真命题,如果是,请写出证明过程;如果不是,请举出反例.
(要求:画出相应的图形,并用文字语言或符号语言进行表述)
16.(2023山东济宁金乡月考)(8分)如图,现有以下3个论断:①AB∥CD;②∠B=∠C;③∠E=∠F.请以其中2个论断为条件,另一个论断为结论构造命题.
(1)你构造的是哪几个命题
(2)请选择其中一个真命题加以证明.
17.(2023山东济南莱芜期中)(8分)如图,△ABC中,CD⊥AB于点D,DE∥BC交AC于点E,EF⊥CD于点G,交BC于点F.
(1)求证:∠ADE=∠EFC;
(2)若∠ACB=72°,∠A=60°,求∠DCB的度数.
18.(8分)如图,BD∥GE,∠AFG=∠1=50°.
(1)求证:AF∥DE;
(2)若AQ平分∠FAC,交BD的延长线于点Q,且∠Q=15°,求∠ACQ的度数.
19.(2022山东泰安新泰期中)(12分)在△ABC中,AE平分∠BAC,∠C>∠B.
(1)如图1,若AD⊥BC于点D,∠B=40°,∠C=60°,求∠EAD的度数;
(2)如图1,根据(1)的解答过程,猜想∠B、∠C、∠EAD之间的数量关系,并说明理由;
(3)如图2,在线段AE上任取一点P(不与点A、E重合),过点P作PD⊥BC于点D,请写出∠B、∠C、∠EPD之间的数量关系,并说明理由.
答案全解全析
1.B 命题有①两点之间线段最短;③不相交的两条直线平行;④对顶角的平分线在同一条直线上.②⑤不是判断,不是命题.故选B.
2.D A,B,C都是性质,D是一元一次方程的定义.故选D.
3.A A项,满足条件,不满足结论,故A选项符合题意;B项,不满足条件,也不满足结论,故B选项不符合题意;C项,满足条件∠1+∠2=90°,也满足结论∠1≠∠2,故C选项不符合题意;D项,不满足条件,也不满足结论,故D选项不符合题意.故选A.
4.C (1)三角形的一个外角不一定大于它的一个内角,故原命题是假命题;
(2)若一个三角形的三个内角的度数之比为1∶3∶4,则三个内角的度数分别为22.5°,67.5°,90°,故这个三角形肯定是直角三角形,故原命题是真命题;
(3)三角形的最小内角不能大于60°,是真命题;
(4)三角形的一个外角等于和它不相邻的两个内角的和,是真命题.
综上,(2)(3)(4)是真命题,共3个,故选C.
5.B A项,∵∠4=∠3,∴DF∥BC,故A不符合题意;
B项,∵∠1=∠4,∴EF∥AB,故B符合题意;
C项,∵∠1=∠B,∴DF∥BC,故C不符合题意;
D项,∵∠4+∠2=180°,∴DF∥BC,故D不符合题意.故选B.
6.C 如图所示,
根据题意可知,AC∥DE∥FG,BD∥CE,DF∥EG,
∵BC∥DE,∴∠1=∠BDE=50°,∴∠EDF=∠2-∠BDE=158°-50°=108°,∵DE∥FG,∴∠DFG=180°-∠EDF=180°-108°=72°,
∵DF∥EG,∴∠3=∠DFG=72°,故选C.
7.B 如图,延长DC交AE于F,
∵AB∥CD,∠BAE=87°,
∴∠CFE=87°,
又∵∠DCE=121°,∴∠E=∠DCE-∠CFE=121°-87°=34°,故选B.
8.C 如图,延长AB交EG于M,延长CD交FG于N,过G作GK∥AB,
∵AB∥CD,∴GK∥CD∥AB,∴∠KGM=∠EMB,∠KGN=∠DNF,
∴∠KGM+∠KGN=∠EMB+∠DNF,∴∠EGF=∠EMB+∠DNF,
∵∠ABE=80°,∠E=47°,∴∠EMB=∠ABE-∠E=33°,同理可得
∠DNF=33°,∴∠EGF=∠EMB+∠DNF=33°+33°=66°.故选C.
9.答案 直角三角形
解析 设三角形的第三个内角度数为x,则另两个内角的度数和为x,由三角形内角和为180°,可得2x=180°,所以x=90°,所以该三角形为直角三角形.
10.答案 如果两个角是同一个角的余角,那么这两个角相等;真
解析 根据命题的特点,可以改写为“如果两个角是同一个角的余角,那么这两个角相等”,这个命题为真命题.
11.答案 105°
解析 如图,设DE交AB于O点,
∵DE∥AC,∴∠DOA=∠A=45°,
∵∠D=90°-∠E=90°-30°=60°,
∴∠1=∠D+∠DOA=60°+45°=105°.
12.答案 160°
解析 如图,延长AB,交DC的延长线于点E,
由题意得,AF∥DE,∴∠A=∠E=130°,
∵∠ABC=150°,∴∠CBE=30°,
∴∠BCD=∠CBE+∠E=30°+130°=160°.
13.答案 57
解析 ∵BC⊥AE,DE⊥AE,∴BC∥DE,∴∠3+∠CBD=180°,
又∵∠2+∠3=180°,∴∠2=∠CBD,∴CF∥DB,∴∠ABD=∠1=66°,
又∵BC平分∠ABD,∴∠DBC=∠ABD=33°,∴∠2=∠DBC=33°,
又∵BC⊥AG,∴∠ACF=90°-∠2=90°-33°=57°,故答案为57.
14.答案 180°
解析 如图,
∵∠1=∠2+∠C,∠2=∠A+∠D,
∴∠1=∠A+∠C+∠D,
∵∠1+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
15.解析 (1)在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行.
(2)是真命题.
已知:如图,AB⊥EF,垂足为B,CD⊥EF,垂足为D,
求证:AB∥CD.
证明:∵AB⊥EF,CD⊥EF,
∴∠ABD=∠CDF=90°,∴AB∥CD.
16.解析 (1)由①②得③;由①③得②;由②③得①.
(2)答案不唯一.
可选择由①②得③,证明过程如下:
∵AB∥CD,∴∠EAB=∠C,
又∵∠B=∠C,∴∠EAB=∠B,∴CE∥BF,∴∠E=∠F.
17.解析 (1)证明:∵DE∥BC,∴∠ADE=∠B,
∵CD⊥AB,EF⊥CD,∴AB∥EF,
∴∠B=∠EFC,∴∠ADE=∠EFC.
(2)∵∠ACB=72°,∠A=60°,
∴∠B=180°-∠A-∠ACB=48°,
∵CD⊥AB,∴∠BDC=90°,
∴∠DCB=180°-90°-48°=42°.
18.解析 (1)证明:∵BD∥GE,∴∠E=∠1=50°,
∵∠AFG=∠1=50°,∴∠E=∠AFG,∴AF∥DE.
(2)∵∠1=50°,∠Q=15°,∴∠AHD=65°,
∵AF∥DE,∴∠FAQ=∠AHD=65°,
∵AQ平分∠FAC,∴∠CAQ=∠FAQ=65°,
∴∠ACQ=180°-∠CAQ-∠Q=180°-65°-15°=100°.
19.解析 (1)∵∠B=40°,∠C=60°,
∴∠BAC=180°-(∠B+∠C)=80°,
∵AE平分∠BAC,
∴∠EAC=∠BAC=×80°=40°,
∵AD⊥BC,∴∠ADC=90°,
∵∠C=60°,∴∠DAC=180°-90°-60°=30°,
∴∠EAD=∠EAC-∠DAC=40°-30°=10°.
(2)∠EAD=(∠C-∠B).
理由:∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-(∠B+∠C),
∵AE平分∠BAC,
∴∠CAE=∠BAC=[180°-(∠B+∠C)]=90°-(∠B+∠C),
∵AD⊥BC,∴∠ADC=90°,∴∠CAD=90°-∠C,
∴∠EAD=∠CAE-∠CAD=90°-(∠B+∠C)-(90°-∠C)=(∠C-∠B),即∠EAD=(∠C-∠B).
(3)∠EPD=∠C-∠B.
理由:如图,过A作AG⊥BC于G,
∵PD⊥BC,∴AG∥PD,∴∠GAE=∠EPD,
∵∠BAC=180°-(∠B+∠C),AE平分∠BAC,
∴∠EAC=∠BAC=[180°-(∠B+∠C)]=90°-∠B-∠C,
∵AG⊥BC,∴∠AGC=90°,
∴∠GAC=90°-∠C,
∴∠GAE=∠CAE-∠CAG=90°-∠B-∠C-(90°-∠C)=∠C-∠B,
∴∠EPD=∠C-∠B.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
