2024鲁教版数学七年级下册--专项素养综合全练(八)确定不等式(组)或方程(组)中字母的值或取值范围(含解析)
文档属性
| 名称 | 2024鲁教版数学七年级下册--专项素养综合全练(八)确定不等式(组)或方程(组)中字母的值或取值范围(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 284.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:44 | ||
图片预览

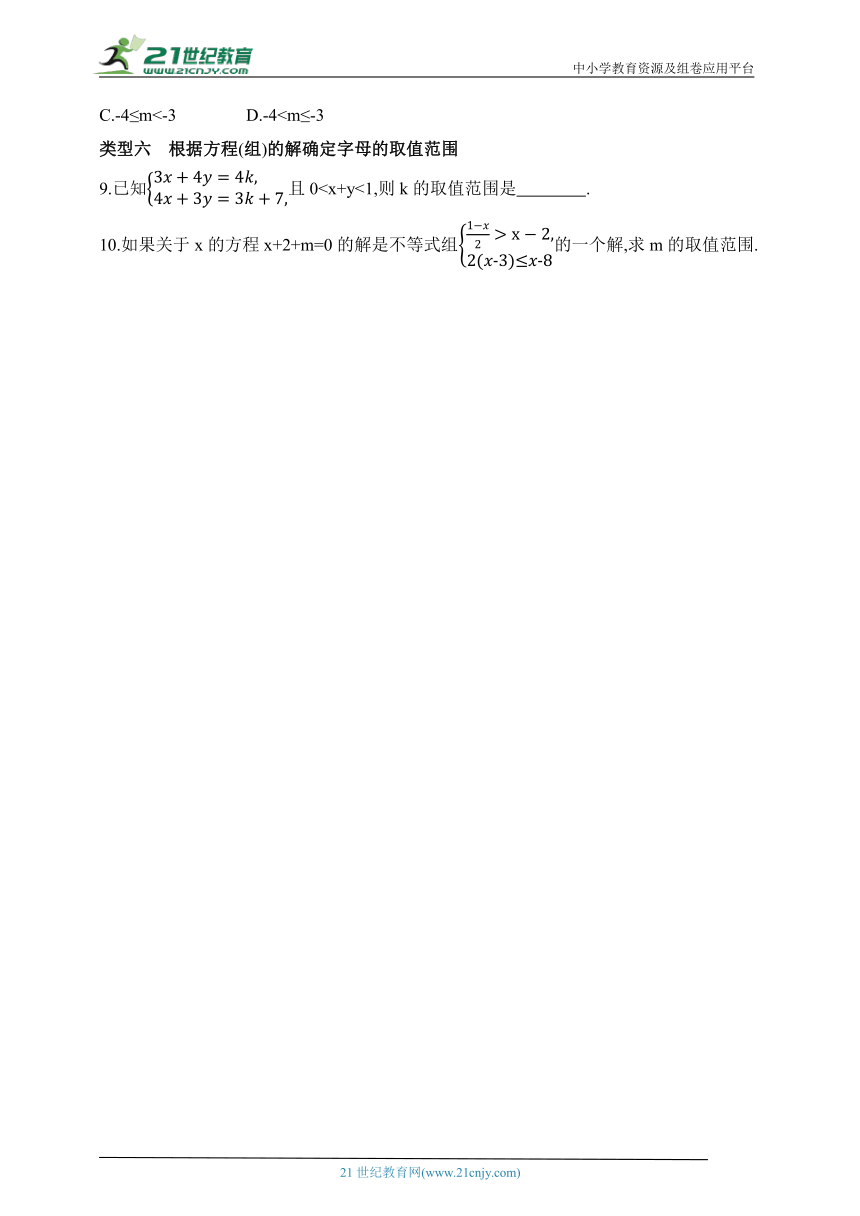
文档简介
中小学教育资源及组卷应用平台
2024鲁教版数学七年级下册
专项素养综合全练(八)
确定不等式(组)或方程(组)中字母的值或取值范围
类型一 根据不等式的概念确定字母的值
1.已知(k-3)x|k|-2+2k>0为关于x的一元一次不等式,则k= .
类型二 根据不等式的基本性质确定字母的取值范围
2.若(m-1)x≤m-1的解集是x≤1,则m的取值范围是( )
A.m>1 B.m≤-1 C.m<1 D.m≥1
类型三 根据不等式(组)的解集确定字母的值或取值范围
3.(2022河南南阳南召期中)如果关于x的不等式4-3a≥2(3x+a)的解集在数轴上表示如图所示,那么a的值是 ( )
A.-1 B.-2 C.2 D.1
4.(2023四川遂宁中考)若关于x的不等式组的解集为x>3,则a的取值范围是( )
A.a>3 B.a<3 C.a≥3 D.a≤3
5.若关于x的一元一次不等式ax-1>0的解集是x>3,则a的值是 .
类型四 根据不等式组无解确定字母的取值范围
6.(2023山东青岛市南期末)若关于x的不等式组无解,则a的取值范围是( )
A.a≤-6 B.a<-6 C.a>3 D.a≥6
类型五 根据不等式(组)的特殊解的个数确定字母的取值范围
7.(2023浙江宁波海曙期末)若关于x的不等式2-m-x>0的正整数解共有3个,则m的取值范围是( )
A.-1≤m<0 B.-1C.-2≤m<-1 D.-28.(2023四川眉山中考)关于x的不等式组的整数解只有4个,则m的取值范围是( )
A.-5≤m<-4 B.-5C.-4≤m<-3 D.-4类型六 根据方程(组)的解确定字母的取值范围
9.已知且010.如果关于x的方程x+2+m=0的解是不等式组的一个解,求m的取值范围.
答案全解全析
1.答案 -3
解析 ∵(k-3)x|k|-2+2k>0为关于x的一元一次不等式,∴∴k=-3.故答案为-3.
2.A ∵(m-1)x≤m-1的解集为x≤1,∴m-1>0,解得m>1.故选A.
3.C 去括号,得4-3a≥6x+2a,移项、合并同类项,得-6x≥5a-4,系数化为1,得x≤.根据数轴得不等式的解集为x≤-1,∴=-1,解得a=2.故选C.
4.D 解不等式①得x>3,解不等式②得x>a,
∵关于x的不等式组的解集为x>3,∴a≤3,故选D.
5.答案
解析 由ax-1>0,得ax>1,∵不等式的解集为x>3,∴a>0,不等式ax>1的两边同时除以a,得x>.
6.D
解不等式①,得x>,解不等式②,得x<3,
∵不等式组无解,∴≥3,解得a≥6.故选D.
7.C 解不等式2-m-x>0,得x<2-m,
∵关于x的不等式2-m-x>0的正整数解共有3个,
∴3<2-m≤4,解得-2≤m<-1.故选C.
8.A
解不等式②得x<3,∴不等式组的解集为m+39.答案 -1解析
①+②,得7x+7y=7k+7,则x+y=k+1,∵010.解析 解不等式组得x≤-2,
由x+2+m=0,得x=-2-m,∵关于x的方程x+2+m=0的解是不等式组的一个解,
∴-2-m≤-2,解得m≥0.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版数学七年级下册
专项素养综合全练(八)
确定不等式(组)或方程(组)中字母的值或取值范围
类型一 根据不等式的概念确定字母的值
1.已知(k-3)x|k|-2+2k>0为关于x的一元一次不等式,则k= .
类型二 根据不等式的基本性质确定字母的取值范围
2.若(m-1)x≤m-1的解集是x≤1,则m的取值范围是( )
A.m>1 B.m≤-1 C.m<1 D.m≥1
类型三 根据不等式(组)的解集确定字母的值或取值范围
3.(2022河南南阳南召期中)如果关于x的不等式4-3a≥2(3x+a)的解集在数轴上表示如图所示,那么a的值是 ( )
A.-1 B.-2 C.2 D.1
4.(2023四川遂宁中考)若关于x的不等式组的解集为x>3,则a的取值范围是( )
A.a>3 B.a<3 C.a≥3 D.a≤3
5.若关于x的一元一次不等式ax-1>0的解集是x>3,则a的值是 .
类型四 根据不等式组无解确定字母的取值范围
6.(2023山东青岛市南期末)若关于x的不等式组无解,则a的取值范围是( )
A.a≤-6 B.a<-6 C.a>3 D.a≥6
类型五 根据不等式(组)的特殊解的个数确定字母的取值范围
7.(2023浙江宁波海曙期末)若关于x的不等式2-m-x>0的正整数解共有3个,则m的取值范围是( )
A.-1≤m<0 B.-1
A.-5≤m<-4 B.-5
9.已知且0
答案全解全析
1.答案 -3
解析 ∵(k-3)x|k|-2+2k>0为关于x的一元一次不等式,∴∴k=-3.故答案为-3.
2.A ∵(m-1)x≤m-1的解集为x≤1,∴m-1>0,解得m>1.故选A.
3.C 去括号,得4-3a≥6x+2a,移项、合并同类项,得-6x≥5a-4,系数化为1,得x≤.根据数轴得不等式的解集为x≤-1,∴=-1,解得a=2.故选C.
4.D 解不等式①得x>3,解不等式②得x>a,
∵关于x的不等式组的解集为x>3,∴a≤3,故选D.
5.答案
解析 由ax-1>0,得ax>1,∵不等式的解集为x>3,∴a>0,不等式ax>1的两边同时除以a,得x>.
6.D
解不等式①,得x>,解不等式②,得x<3,
∵不等式组无解,∴≥3,解得a≥6.故选D.
7.C 解不等式2-m-x>0,得x<2-m,
∵关于x的不等式2-m-x>0的正整数解共有3个,
∴3<2-m≤4,解得-2≤m<-1.故选C.
8.A
解不等式②得x<3,∴不等式组的解集为m+3
①+②,得7x+7y=7k+7,则x+y=k+1,∵0
由x+2+m=0,得x=-2-m,∵关于x的方程x+2+m=0的解是不等式组的一个解,
∴-2-m≤-2,解得m≥0.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
