2024鲁教版数学七年级下册--专项素养综合全练(六)三角形全等常见模型(含解析)
文档属性
| 名称 | 2024鲁教版数学七年级下册--专项素养综合全练(六)三角形全等常见模型(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 350.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024鲁教版数学七年级下册
专项素养综合全练(六)
三角形全等常见模型
类型一 平移模型
1.(2023福建福州模拟)如图,已知AB=DE,BE=CF,AC=DF,求证:AB∥DE.
类型二 旋转模型
(2023广东广州荔湾期末)如图,在△ABC和△ADE中,∠BAC=
∠DAE=90°,AB=AC,AD=AE,C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)猜想BD,CE有何特殊位置关系,并说明理由.
类型三 对称模型
3.如图,CA=CB,点E、D分别是CA、CB的中点.求证:∠A=∠B.
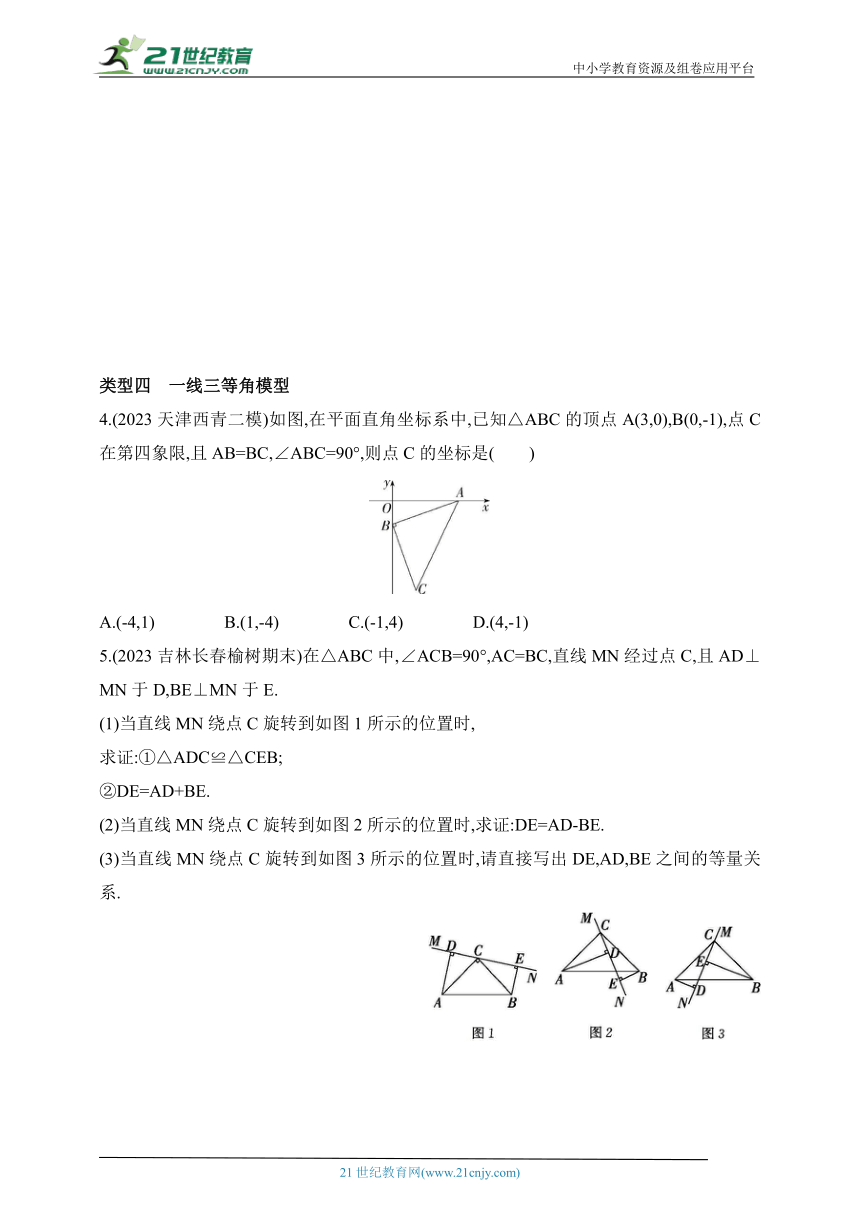
类型四 一线三等角模型
4.(2023天津西青二模)如图,在平面直角坐标系中,已知△ABC的顶点A(3,0),B(0,-1),点C在第四象限,且AB=BC,∠ABC=90°,则点C的坐标是( )
A.(-4,1) B.(1,-4) C.(-1,4) D.(4,-1)
5.(2023吉林长春榆树期末)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到如图1所示的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE.
(2)当直线MN绕点C旋转到如图2所示的位置时,求证:DE=AD-BE.
(3)当直线MN绕点C旋转到如图3所示的位置时,请直接写出DE,AD,BE之间的等量关系.
答案全解全析
1.证明 ∵BE=CF,∴BE+EC=CF+CE,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS),∴∠B=∠DEF,∴AB∥DE.
2.解析 (1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
(2)BD⊥CE.理由如下:
如图,设AC与BD交于点G,
∵△BAD≌△CAE,
∴∠ACE=∠ABD,
∵∠AGB=∠CGD,∠BAC=90°,
∴∠CDG=90°,∴BD⊥CE.
3.证明 ∵点E、D分别是CA、CB的中点,
∴CE=CB,∵CA=CB,∴CE=CD,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴∠A=∠B.
4.B 如图,
过点C作CE⊥y轴于E,∵∠ABC=90°,∴∠ABO+∠CBE=90°,
∵∠AOB=90°,∴∠ABO+∠BAO=90°,∴∠BAO=∠CBE,
在△AOB与△BEC中,
∴△AOB≌△BEC(AAS),∴OB=EC=1,BE=OA=3,
∴OE=OB+BE=1+3=4,∴点C的坐标为(1,-4),故选B.
5.解析 (1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠ACB=∠CEB=90°,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS).
②∵△ADC≌△CEB,∴AD=CE,CD=BE,
∴DE=CE+CD=AD+BE.
(2)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,
∴DE=CE-CD=AD-BE.
(3)DE=BE-AD.
详解:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,
∴DE=CD-CE=BE-AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版数学七年级下册
专项素养综合全练(六)
三角形全等常见模型
类型一 平移模型
1.(2023福建福州模拟)如图,已知AB=DE,BE=CF,AC=DF,求证:AB∥DE.
类型二 旋转模型
(2023广东广州荔湾期末)如图,在△ABC和△ADE中,∠BAC=
∠DAE=90°,AB=AC,AD=AE,C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)猜想BD,CE有何特殊位置关系,并说明理由.
类型三 对称模型
3.如图,CA=CB,点E、D分别是CA、CB的中点.求证:∠A=∠B.
类型四 一线三等角模型
4.(2023天津西青二模)如图,在平面直角坐标系中,已知△ABC的顶点A(3,0),B(0,-1),点C在第四象限,且AB=BC,∠ABC=90°,则点C的坐标是( )
A.(-4,1) B.(1,-4) C.(-1,4) D.(4,-1)
5.(2023吉林长春榆树期末)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到如图1所示的位置时,
求证:①△ADC≌△CEB;
②DE=AD+BE.
(2)当直线MN绕点C旋转到如图2所示的位置时,求证:DE=AD-BE.
(3)当直线MN绕点C旋转到如图3所示的位置时,请直接写出DE,AD,BE之间的等量关系.
答案全解全析
1.证明 ∵BE=CF,∴BE+EC=CF+CE,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS),∴∠B=∠DEF,∴AB∥DE.
2.解析 (1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS).
(2)BD⊥CE.理由如下:
如图,设AC与BD交于点G,
∵△BAD≌△CAE,
∴∠ACE=∠ABD,
∵∠AGB=∠CGD,∠BAC=90°,
∴∠CDG=90°,∴BD⊥CE.
3.证明 ∵点E、D分别是CA、CB的中点,
∴CE=CB,∵CA=CB,∴CE=CD,
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS),∴∠A=∠B.
4.B 如图,
过点C作CE⊥y轴于E,∵∠ABC=90°,∴∠ABO+∠CBE=90°,
∵∠AOB=90°,∴∠ABO+∠BAO=90°,∴∠BAO=∠CBE,
在△AOB与△BEC中,
∴△AOB≌△BEC(AAS),∴OB=EC=1,BE=OA=3,
∴OE=OB+BE=1+3=4,∴点C的坐标为(1,-4),故选B.
5.解析 (1)证明:①∵AD⊥MN,BE⊥MN,
∴∠ADC=∠ACB=∠CEB=90°,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS).
②∵△ADC≌△CEB,∴AD=CE,CD=BE,
∴DE=CE+CD=AD+BE.
(2)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,
∴DE=CE-CD=AD-BE.
(3)DE=BE-AD.
详解:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=∠ACB=90°,
∴∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,
∴DE=CD-CE=BE-AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
