2024鲁教版数学七年级下册--专项素养综合全练(四)三角形内角和的常见应用类型(含解析)
文档属性
| 名称 | 2024鲁教版数学七年级下册--专项素养综合全练(四)三角形内角和的常见应用类型(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 417.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024鲁教版数学七年级下册
专项素养综合全练(四)
三角形内角和的常见应用类型
类型一 三角形内角和定理在求角度中的应用
(2023山东济南期中)如图,在△ABC中,∠A=40°,∠B=56°,CE平分
∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.
类型二 三角形内角和定理在折叠中的应用
2.(2023辽宁本溪、铁岭、辽阳中考)如图,在三角形纸片ABC中,AB=AC,∠B=20°,点D是边BC上的动点,将三角形纸片沿AD折叠,使点B落在点B'处,当B'D⊥BC时,∠BAD的度数为 .
类型三 三角形内角和定理在类比思想中的应用
3.【新考向·新定义试题】(2022北京房山期末)如图,由线段AB,AM,CM,CD组成的图形像,称为“形BAMCD”.
(1)如图1,形BAMCD中,若AB∥CD,∠AMC=60°,则∠A+∠C
= °;
(2)如图2,连接形BAMCD中B,D两点,若∠ABD+∠BDC=160°,
∠AMC=α,试猜想∠BAM与∠MCD之间的数量关系,并说明理由.
类型四 三角形内角和定理在转化思想中的应用
4.(2023山东淄博期中)如图,∠A+∠B+∠C+∠D+∠E=( )
A.180° B.260° C.270° D.360°
类型五 三角形内、外角的关系在探究角的关系中的应用
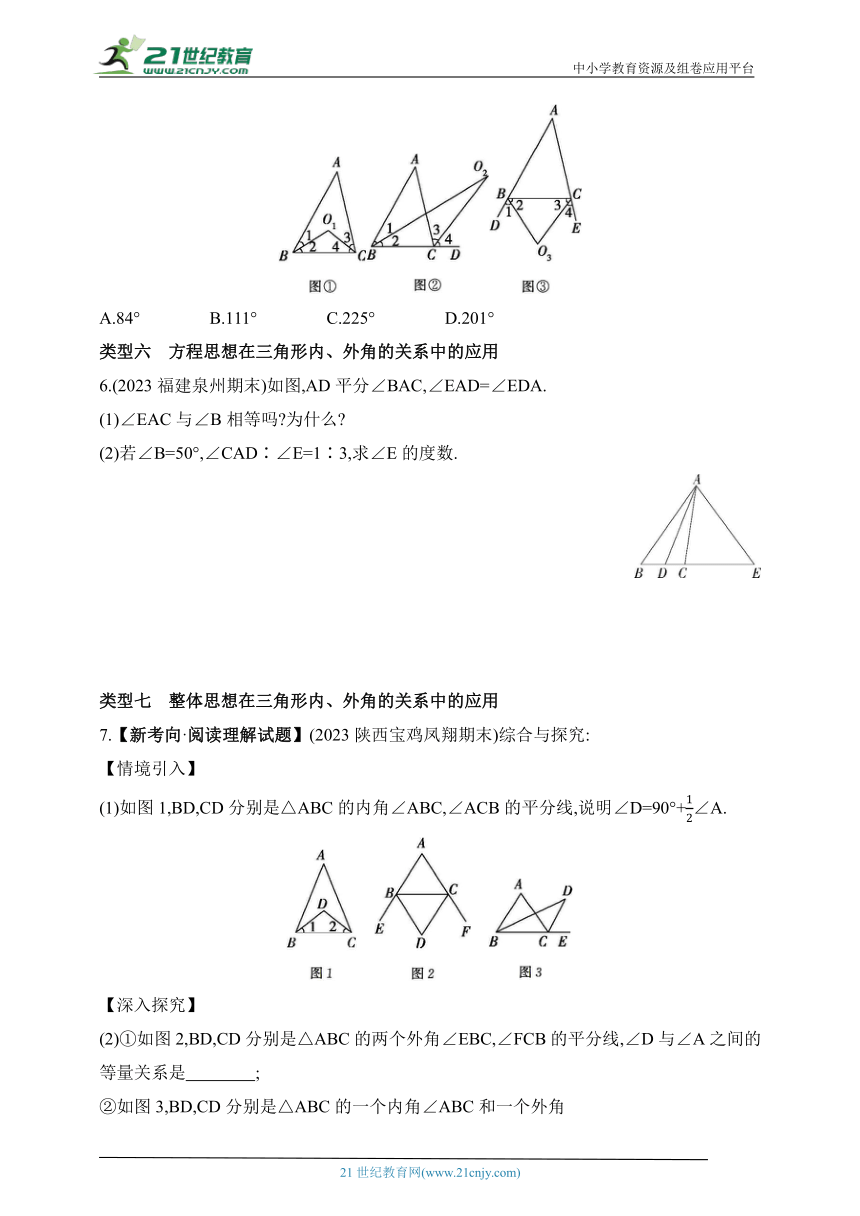
5.(2023山东东营广饶期中)如图①②③,若∠A=42°,∠1=∠2,∠3=∠4,则∠O1+∠O2+∠O3=( )
A.84° B.111° C.225° D.201°
类型六 方程思想在三角形内、外角的关系中的应用
6.(2023福建泉州期末)如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗 为什么
(2)若∠B=50°,∠CAD∶∠E=1∶3,求∠E的度数.
类型七 整体思想在三角形内、外角的关系中的应用
7.【新考向·阅读理解试题】(2023陕西宝鸡凤翔期末)综合与探究:
【情境引入】
(1)如图1,BD,CD分别是△ABC的内角∠ABC,∠ACB的平分线,说明∠D=90°+∠A.
【深入探究】
(2)①如图2,BD,CD分别是△ABC的两个外角∠EBC,∠FCB的平分线,∠D与∠A之间的等量关系是 ;
②如图3,BD,CD分别是△ABC的一个内角∠ABC和一个外角
∠ACE的平分线,BD,CD交于点D,探究∠D与∠A之间的等量关系,并说明理由.
答案全解全析
1.解析 在△ABC中,∠A=40°,∠B=56°,
∴∠ACB=180°-∠A-∠B=180°-40°-56°=84°,
∵CE平分∠ACB,∴∠BCE=∠ACB=×84°=42°.
∵CD⊥AB,∴∠BDC=90°,
∴∠BCD=90°-∠B=90°-56°=34°,
∴∠DCE=∠BCE-∠BCD=42°-34°=8°.
∵DF⊥CE,∴∠CFD=90°,
∴∠CDF=90°-∠DCF=90°-8°=82°.
2.答案 25°或115°
解析 由折叠的性质得∠ADB'=∠ADB.
∵B'D⊥BC,∴∠BDB'=90°.
①当B'在BC下方时,如图,∵∠ADB+∠ADB'+∠BDB'=360°,
∴∠ADB=×(360°-90°)=135°,∴∠BAD=180°-∠B-∠ADB
=25°;
②当B'在BC上方时,如图,∵∠ADB+∠ADB'=90°,
∴∠ADB=×90°=45°,
∴∠BAD=180°-∠B-∠ADB=115°.
综上,∠BAD的度数为25°或115°.
故答案为25°或115°.
3.解析 (1)如图,延长AM交CD于E,
∵AB∥CD,∴∠A=∠AEC,
∴∠A+∠C=∠C+∠MEC=∠AMC=60°.
故答案为60.
(2)∠BAM+∠MCD=α+20°.
理由:如图,过A点作AP∥CD交BD于点P,
∴∠APB=∠D,
∵∠BAP+∠APB+∠B=180°,∠B+∠D=160°,
∴∠BAP=180°-160°=20°,
由(1)可得∠AMC=∠PAM+∠MCD,
∵∠AMC=α,∴∠PAM+∠MCD=α,
∴∠BAM+∠MCD=α+20°.
4.A 如图,
∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,故选A.
5.D ∵∠A=42°,∠1=∠2,∠3=∠4,
∴题图①中,∠2+∠4=(∠1+∠2+∠3+∠4)=×(180°-42°)=69°,故∠O1=180°-69°=111°;
题图②中,∠O2=∠4-∠2=×[(∠3+∠4)-(∠1+∠2)]=∠A=21°;
题图③中,∠ABC+∠ACB=180°-∠A=180°-42°=138°,则∠1+∠2
+∠3+∠4=180°+180°-138°=222°,故∠O3=180°-(∠2+∠3)
=180°-×222°=69°.∴∠O1+∠O2+∠O3=111°+21°+69°=201°,故选D.
解析 (1)相等.理由如下:∵AD平分∠BAC,∴∠BAD=∠CAD.
又∠EAD=∠EDA,∴∠EAC=∠EAD-∠CAD=∠EDA-∠BAD=∠B.
(2)设∠CAD=x°,则∠E=3x°,由(1)知∠EAC=∠B=50°,∴∠EAD=∠EDA=(x+50)°.在△EAD中,∵∠E+∠EAD+∠EDA=180°,
∴3x+2(x+50)=180,解得x=16.∴∠E=48°.
解析 (1)证明:∵BD,CD分别是△ABC的内角∠ABC,∠ACB的平分线,∴∠1=∠ABC,∠2=∠ACB,∵∠1+∠2+∠D=180°,∠A+
∠ABC+∠ACB=180°,∴∠D=180°-∠1-∠2=180°-(∠ABC+
∠ACB)=180°-(180°-∠A)=90°+∠A.
(2)①∵BD,CD分别是△ABC的两个外角∠EBC,∠FCB的平分线,
∴∠DBC=∠EBC=(∠A+∠ACB),∠DCB=∠FCB=(∠A+∠ABC),∵∠DBC+∠DCB+∠D=180°,∠A+∠ABC+∠ACB=180°,∴∠D=180°-∠DBC-∠DCB=180°-(∠A+∠ACB+∠A+∠ABC)=180°-(180°+∠A)=90°-∠A.故答案为∠D=90°-∠A.
②∠D=∠A.理由如下:∵BD,CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,∴∠DBC=∠ABC,∠DCE=∠ACE,
∵∠ACE=∠A+∠ABC,∠DCE=∠D+∠DBC,∴∠D+∠ABC=(∠A+∠ABC),∴∠D=∠A.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024鲁教版数学七年级下册
专项素养综合全练(四)
三角形内角和的常见应用类型
类型一 三角形内角和定理在求角度中的应用
(2023山东济南期中)如图,在△ABC中,∠A=40°,∠B=56°,CE平分
∠ACB,CD⊥AB于点D,DF⊥CE于点F,求∠CDF的度数.
类型二 三角形内角和定理在折叠中的应用
2.(2023辽宁本溪、铁岭、辽阳中考)如图,在三角形纸片ABC中,AB=AC,∠B=20°,点D是边BC上的动点,将三角形纸片沿AD折叠,使点B落在点B'处,当B'D⊥BC时,∠BAD的度数为 .
类型三 三角形内角和定理在类比思想中的应用
3.【新考向·新定义试题】(2022北京房山期末)如图,由线段AB,AM,CM,CD组成的图形像,称为“形BAMCD”.
(1)如图1,形BAMCD中,若AB∥CD,∠AMC=60°,则∠A+∠C
= °;
(2)如图2,连接形BAMCD中B,D两点,若∠ABD+∠BDC=160°,
∠AMC=α,试猜想∠BAM与∠MCD之间的数量关系,并说明理由.
类型四 三角形内角和定理在转化思想中的应用
4.(2023山东淄博期中)如图,∠A+∠B+∠C+∠D+∠E=( )
A.180° B.260° C.270° D.360°
类型五 三角形内、外角的关系在探究角的关系中的应用
5.(2023山东东营广饶期中)如图①②③,若∠A=42°,∠1=∠2,∠3=∠4,则∠O1+∠O2+∠O3=( )
A.84° B.111° C.225° D.201°
类型六 方程思想在三角形内、外角的关系中的应用
6.(2023福建泉州期末)如图,AD平分∠BAC,∠EAD=∠EDA.
(1)∠EAC与∠B相等吗 为什么
(2)若∠B=50°,∠CAD∶∠E=1∶3,求∠E的度数.
类型七 整体思想在三角形内、外角的关系中的应用
7.【新考向·阅读理解试题】(2023陕西宝鸡凤翔期末)综合与探究:
【情境引入】
(1)如图1,BD,CD分别是△ABC的内角∠ABC,∠ACB的平分线,说明∠D=90°+∠A.
【深入探究】
(2)①如图2,BD,CD分别是△ABC的两个外角∠EBC,∠FCB的平分线,∠D与∠A之间的等量关系是 ;
②如图3,BD,CD分别是△ABC的一个内角∠ABC和一个外角
∠ACE的平分线,BD,CD交于点D,探究∠D与∠A之间的等量关系,并说明理由.
答案全解全析
1.解析 在△ABC中,∠A=40°,∠B=56°,
∴∠ACB=180°-∠A-∠B=180°-40°-56°=84°,
∵CE平分∠ACB,∴∠BCE=∠ACB=×84°=42°.
∵CD⊥AB,∴∠BDC=90°,
∴∠BCD=90°-∠B=90°-56°=34°,
∴∠DCE=∠BCE-∠BCD=42°-34°=8°.
∵DF⊥CE,∴∠CFD=90°,
∴∠CDF=90°-∠DCF=90°-8°=82°.
2.答案 25°或115°
解析 由折叠的性质得∠ADB'=∠ADB.
∵B'D⊥BC,∴∠BDB'=90°.
①当B'在BC下方时,如图,∵∠ADB+∠ADB'+∠BDB'=360°,
∴∠ADB=×(360°-90°)=135°,∴∠BAD=180°-∠B-∠ADB
=25°;
②当B'在BC上方时,如图,∵∠ADB+∠ADB'=90°,
∴∠ADB=×90°=45°,
∴∠BAD=180°-∠B-∠ADB=115°.
综上,∠BAD的度数为25°或115°.
故答案为25°或115°.
3.解析 (1)如图,延长AM交CD于E,
∵AB∥CD,∴∠A=∠AEC,
∴∠A+∠C=∠C+∠MEC=∠AMC=60°.
故答案为60.
(2)∠BAM+∠MCD=α+20°.
理由:如图,过A点作AP∥CD交BD于点P,
∴∠APB=∠D,
∵∠BAP+∠APB+∠B=180°,∠B+∠D=160°,
∴∠BAP=180°-160°=20°,
由(1)可得∠AMC=∠PAM+∠MCD,
∵∠AMC=α,∴∠PAM+∠MCD=α,
∴∠BAM+∠MCD=α+20°.
4.A 如图,
∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,故选A.
5.D ∵∠A=42°,∠1=∠2,∠3=∠4,
∴题图①中,∠2+∠4=(∠1+∠2+∠3+∠4)=×(180°-42°)=69°,故∠O1=180°-69°=111°;
题图②中,∠O2=∠4-∠2=×[(∠3+∠4)-(∠1+∠2)]=∠A=21°;
题图③中,∠ABC+∠ACB=180°-∠A=180°-42°=138°,则∠1+∠2
+∠3+∠4=180°+180°-138°=222°,故∠O3=180°-(∠2+∠3)
=180°-×222°=69°.∴∠O1+∠O2+∠O3=111°+21°+69°=201°,故选D.
解析 (1)相等.理由如下:∵AD平分∠BAC,∴∠BAD=∠CAD.
又∠EAD=∠EDA,∴∠EAC=∠EAD-∠CAD=∠EDA-∠BAD=∠B.
(2)设∠CAD=x°,则∠E=3x°,由(1)知∠EAC=∠B=50°,∴∠EAD=∠EDA=(x+50)°.在△EAD中,∵∠E+∠EAD+∠EDA=180°,
∴3x+2(x+50)=180,解得x=16.∴∠E=48°.
解析 (1)证明:∵BD,CD分别是△ABC的内角∠ABC,∠ACB的平分线,∴∠1=∠ABC,∠2=∠ACB,∵∠1+∠2+∠D=180°,∠A+
∠ABC+∠ACB=180°,∴∠D=180°-∠1-∠2=180°-(∠ABC+
∠ACB)=180°-(180°-∠A)=90°+∠A.
(2)①∵BD,CD分别是△ABC的两个外角∠EBC,∠FCB的平分线,
∴∠DBC=∠EBC=(∠A+∠ACB),∠DCB=∠FCB=(∠A+∠ABC),∵∠DBC+∠DCB+∠D=180°,∠A+∠ABC+∠ACB=180°,∴∠D=180°-∠DBC-∠DCB=180°-(∠A+∠ACB+∠A+∠ABC)=180°-(180°+∠A)=90°-∠A.故答案为∠D=90°-∠A.
②∠D=∠A.理由如下:∵BD,CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,∴∠DBC=∠ABC,∠DCE=∠ACE,
∵∠ACE=∠A+∠ABC,∠DCE=∠D+∠DBC,∴∠D+∠ABC=(∠A+∠ABC),∴∠D=∠A.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
