2024青岛版数学七年级下册--第9章《平行线》素养综合检测(含解析)
文档属性
| 名称 | 2024青岛版数学七年级下册--第9章《平行线》素养综合检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 577.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024青岛版数学七年级下册
第9章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.下列说法中,正确的是( )
A.两条不相交的直线叫做平行线
B.一条直线的平行线有且只有一条
C.若直线a∥b,a∥c,则b∥c
D.若两条线段不相交,则它们互相平行
2.【跨学科·物理】(2023四川凉山州中考)光线在不同介质中的传播速度是不同的,因此光线从水中射向空气中时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,两平行光线从水中射入空气中,∠1=45°,∠2=120°,则∠3+∠4=( )
A.165° B.155° C.105° D.90°
3.(2022山东泰安肥城期末)如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
4.(2023湖南邵阳中考)如图,直线a,b被直线c所截,已知a∥b,∠1=50°,则∠2的大小为( )
A.40° B.50° C.70° D.130°
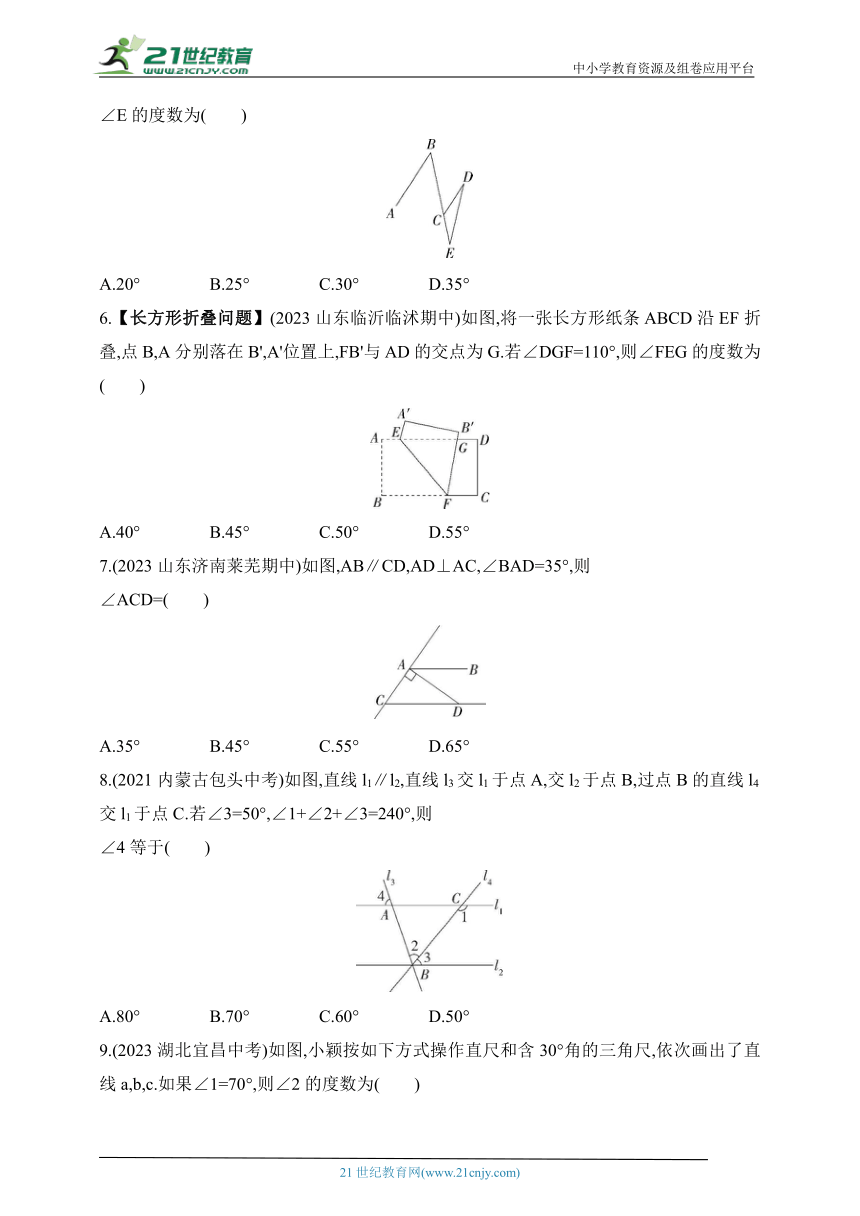
5.(2023辽宁大连中考)如图,直线AB∥CD,∠ABE=45°,∠D=20°,则
∠E的度数为( )
A.20° B.25° C.30° D.35°
6.【长方形折叠问题】(2023山东临沂临沭期中)如图,将一张长方形纸条ABCD沿EF折叠,点B,A分别落在B',A'位置上,FB'与AD的交点为G.若∠DGF=110°,则∠FEG的度数为( )
A.40° B.45° C.50° D.55°
7.(2023山东济南莱芜期中)如图,AB∥CD,AD⊥AC,∠BAD=35°,则
∠ACD=( )
A.35° B.45° C.55° D.65°
8.(2021内蒙古包头中考)如图,直线l1∥l2,直线l3交l1于点A,交l2于点B,过点B的直线l4交l1于点C.若∠3=50°,∠1+∠2+∠3=240°,则
∠4等于( )
A.80° B.70° C.60° D.50°
9.(2023湖北宜昌中考)如图,小颖按如下方式操作直尺和含30°角的三角尺,依次画出了直线a,b,c.如果∠1=70°,则∠2的度数为( )
A.110° B.70°
C.40° D.30°
10.(2023湖北荆州中考)如图所示的“箭头”图形中,AB∥CD,∠B=
∠D=80°,∠E=∠F=47°,则图中∠G的度数是( )
A.80° B.76°
C.66° D.56°
11.如果两个角的两边分别平行,且其中一个角的度数比另一个角的度数的4倍少30°,那么这两个角的度数分别是( )
A.42°、138°
B.10°、10°
C.42°、138°或42°、10°
D.10°、10°或42°、138°
12.【平行线拐点模型】如图,AB∥EF,∠C=90°,则∠α、∠β、∠γ的关系是( )
A.∠β+∠γ-∠α=90°
B.∠α+∠β+∠γ=180°
C.∠α+∠β-∠γ=90°
D.∠β=∠α+∠γ
二、填空题(每小题3分,共18分)
13.在同一平面内有三条直线,如果其中有且只有两条直线相互平行,那么这三条直线有且只有 个交点.
14.(2023湖南永州中考)如图,AB∥CD,BC∥ED,∠B=80°,则∠D= 度.
15.【新考法】(2022山东济南二十八中期中)如图,点A,B,C,D在同一条直线上,若满足条件 ,则有AE∥BF.(要求:不再添加辅助线,只需填一个答案即可)
16.(2023浙江杭州中考)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,点F在线段BC的延长线上.若∠ADE=28°,∠ACF=118°,则∠A= °.
17.(2023内蒙古通辽中考)将一副三角尺按如图所示的方式放置,其中AB∥DE,则∠CDF= 度.
18.两条平行直线被第三条直线所截,有下列结论:
①一对同位角的平分线互相平行;
②一对内错角的平分线互相平行;
③一对同旁内角的平分线互相平行;
④一对同旁内角的平分线互相垂直.
其中结论正确的是 .(填序号)
三、解答题(共46分)
19.(2023山东青岛二十六中期末)(6分)如图,已知CD是∠ACB的平分线,∠A=70°,∠B=60°,DE∥BC.求∠EDC的度数.
20.(6分)如图,直线CD与直线 AB 相交于点C.
(1)根据下列语句画图:
①过点P作PQ∥CD,交AB于点Q.
②过点P作PR⊥CD,垂足为R.
(2)若∠DCB=120°,猜想∠PQC的度数,并说明理由.
21.(2023山东济南济阳期中)(7分)如图,AB∥CD,CE平分∠DCB,
∠E=∠3.求证:DE∥BC.
22.(2023山东青岛黄岛期中)(8分)如图,已知∠ADE=∠BFG,∠BAC+∠AED=180°.
(1)∠BAC与哪个角相等 为什么
(2)试判断AD与FG有怎样的位置关系,请说明理由.
(3)若AD⊥BC,∠BFG=30°,求∠B的度数.
23.(8分)如图,把一张长方形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF应为多少度,才能使AB'∥BD
24.(2023山东青岛市南期中)(11分)已知直线MN∥PQ,点A在直线MN上,点B,C为平面内两点,AC⊥BC于点C.
(1)如图1,当点B在直线MN上,点C在直线MN上方时,延长CB交直线PQ于点D,则∠CAB和∠CDP之间的数量关系是 .
(2)如图2,当点C在直线MN上且在点A左侧,点B在直线MN与PQ之间时,过点B作BD⊥AB交直线PQ于点D.为探究∠ABC与∠BDP之间的数量关系,小明过点B作BF∥MN,请根据他的思路,写出∠ABC与∠BDP的关系,并说明理由.
(3)请从下面A,B两题中任选一题作答.
A.如图3,在(2)的条件下,作∠ABD的平分线交直线MN于点E,当∠AEB=2∠ABC时,直接写出∠ABC的度数.
B.如图4,当点C在直线MN上且在点A左侧,点B在直线PQ下方时,过点B作BD⊥AB交直线PQ于点D,作∠ABD的平分线交直线MN于点E,当∠BDP=2∠BEN时,直接写出∠ABC的度数.
答案全解全析
1.C 在同一平面内,两条不相交的直线叫做平行线,故A错误;过直线外一点,有且只有一条直线与已知直线平行,而一条直线的平行线有无数条,故B错误;平行于同一直线的两条直线平行,故C正确;根据平行线的定义可知D是错误的.故选C.
2.C ∵在水中平行的光线,在空气中也是平行的,∠1=45°,∠2=120°,题图中两光线平行,
∴∠3=∠1=45°,
∵水面与杯底面平行,∴∠4=180°-∠2=60°,
∴∠3+∠4=105°.故选C.
3.C ①∠1与∠4不是内错角,原说法错误;②∠1与∠2是同位角,原说法正确;③∠2与∠4不是内错角,原说法错误;④∠4与∠5是同旁内角,原说法正确;⑤∠2与∠4不是同位角,原说法错误;⑥∠2与∠5是内错角,原说法正确.正确的有3个.故选C.
4.B 如图所示:
∵a∥b,∴∠2=∠3,
∵∠1=∠3,∠1=50°,∴∠1=∠2=50°.故选B.
5.B ∵AB∥CD,∴∠ABE=∠BCD=45°,∴∠DCE=135°.
∴∠E=180°-∠DCE-∠D=180°-135°-20°=25°.故选B.
6.D 由题意知AD∥BC,∴∠BFG=∠DGF=110°.
由折叠的性质可知∠BFE=∠EFG=∠BFG=55°,
∵AD∥BC,∴∠FEG=∠BFE=55°.故选D.
方法解读 长方形折叠问题的解题步骤如下:
第一步:还原;第二步:标出所有相等的角;第三步:找内错角(相等)、同位角(相等)和同旁内角(互补);第四步:计算.
7.C ∵AD⊥AC,∴∠CAD=90°,
∵AB∥CD,∴∠DCA+∠CAB=180°,
又∵∠BAD=35°,
∴∠ACD=180°-∠CAD-∠BAD=55°,故选C.
8.B 如图,
因为l1∥l2,所以∠1+∠3=180°,
因为∠1+∠2+∠3=240°,
所以∠2=240°-(∠1+∠3)=60°.
因为∠3+∠2+∠5=180°,∠3=50°,
所以∠5=180°-∠2-∠3=70°,
因为l1∥l2,所以∠4=∠5=70°,故选B.
9.C 如图,由题意得∠4=30°,b∥c,
∴∠3=∠1=70°,∴∠6=110°.
∵∠4+∠5+∠6=180°,∴∠4+∠5=70°,∴∠5=40°,
∴∠2=∠5=40°,故选C.
10.C 如图,延长AB交EG于M,延长CD交FG于N,过G作GK∥AB,
∵AB∥CD,∴GK∥AB∥CD,
∴∠KGM=∠EMB,∠KGN=∠DNF,
∴∠KGM+∠KGN=∠EMB+∠DNF,
∴∠EGF=∠EMB+∠DNF,
∵∠ABE=80°,∴∠EBM=100°,∵∠E=47°,
∴∠EMB=180°-∠MBE-∠E=33°,
同理:∠DNF=33°,
∴∠EGF=∠EMB+∠DNF=33°+33°=66°.故选C.
11.D 设其中一个角的度数为x°,则另一个角的度数为(4x-30)°,
分两种情况:(1)若两个角的度数相等,则x=4x-30,解得x=10,则4x-30=4×10-30=10;
(2)若两个角互补,则x+(4x-30)=180,解得x=42,则4x-30=4×42-30=138.
故这两个角的度数分别是10°、10°或42°、138°.
故选D.
12.C 如图,分别过点C、D作CM∥AB,DN∥AB,
因为AB∥EF,所以AB∥CM∥ND∥EF,
所以∠1=∠α,∠2=∠3,∠4=∠γ.
由图知∠1+∠2=∠BCD=90°,∠3+∠4=∠β,
所以∠α+∠2=90°,∠3+∠γ=∠β,
即∠2=90°-∠α,∠3=∠β-∠γ,
所以90°-∠α=∠β-∠γ,即∠α+∠β-∠γ=90°.
方法解读 平行线拐点模型:
①辅助线:过拐点作平行线,且有多少个拐点就作多少条平行线;②所有朝左的角的度数之和等于所有朝右的角的度数之和.
13.2
解析 在同一平面内有三条直线,如果其中有且只有两条直线相互平行,那么第三条直线与这两条平行直线分别相交,所以这三条直线有且只有2个交点.
14.100
解析 ∵AB∥CD,∠B=80°,∴∠BCD=∠B=80°,
∵BC∥ED,∴∠D+∠BCD=180°,∴∠D=100°.
15.∠5=∠A(答案不唯一)
解析 添加∠5=∠A,可根据“同位角相等,两直线平行”判定AE∥BF.(答案不唯一)
16.90
解析 ∵DE∥BC,∴∠B=∠ADE=28°,
∵∠ACF=118°,∴∠ACB=62°.∵∠A+∠B+∠ACB=180°,
∴∠A+∠B=118°,
∴∠A=118°-∠B=118°-28°=90°.
17.105
解析 ∵AB∥DE,∴∠BDE=∠B=30°,
∴∠CDF=180°-∠EDF-∠BDE=180°-45°-30°=105°.
18.①②④
解析 ①两直线平行,同位角相等,其角平分线分得的角也相等,根据同位角相等,两直线平行可判定一对同位角的平分线互相平行;②两直线平行,内错角相等,其角平分线分得的角也相等,根据内错角相等,两直线平行可判定一对内错角的平分线互相平行;③显然不对;④两直线平行,同旁内角互补,其角平分线分得的不同的两角互余,从而推出一对同旁内角的平分线互相垂直.
综上,结论正确的是①②④.
19.解析 ∵CD是∠ACB的平分线,
∴∠DCB=∠ACB,
∵DE∥BC,∴∠EDC=∠DCB,∴∠EDC=∠ACB,
∵∠A=70°,∠B=60°,∴∠ACB=180°-(∠A+∠B)=180°-(70°+60°)=50°,
∴∠EDC=∠ACB=×50°=25°,
∴∠EDC的度数为25°.
20.解析 (1)①如图所示,PQ即为所求.
②如图所示,PR即为所求.
(2)∠PQC=60°.理由如下:
因为PQ∥CD,所以∠DCB+∠PQC=180°,
因为∠DCB=120°,
所以∠PQC=180°-∠DCB=180°-120°=60°.
21.证明 ∵AB∥CD,∴∠3=∠2,
∵∠E=∠3,∴∠2=∠E,
∵CE平分∠DCB,∴∠1=∠2=∠BCD,
∴∠E=∠1,∴DE∥BC.
22.解析 (1)∠BAC=∠CED.理由如下:
∵∠BAC+∠AED=180°,∠CED+∠AED=180°,
∴∠BAC=∠CED(同角的补角相等).
(2)AD∥FG.理由如下:
∵∠BAC=∠CED,∴AB∥DE,∴∠BAD=∠ADE,
∵∠ADE=∠BFG,∴∠BFG=∠BAD,∴AD∥FG.
(3)∵AD⊥BC,AD∥FG,∴FG⊥BC,
∴∠FGB=90°,∴∠B+∠BFG=90°,
∵∠BFG=30°,∴∠B=60°.
23.解析 ∠BAF应为55°.理由如下:
因为四边形ABCD是长方形,
所以AD∥BC,∠ABC=90°,
因为∠ADB=20°,所以∠DBC=∠ADB=20°,
所以∠ABD=70°.
要使AB'∥BD,需使∠ABD+∠BAB'=180°,
即∠BAB'=110°,
由折叠的性质知∠BAF=∠B'AF,
所以∠BAF=∠BAB'=55°.
24.解析 (1)∵AC⊥BC,∴∠CAB+∠CBA=90°,
∵MN∥PQ,∴∠CBA=∠CDP,∴∠CAB+∠CDP=90°,
故答案为∠CAB+∠CDP=90°.
(2)∠ABC=∠BDP,理由如下:
∵BF∥MN,MN∥PQ,∴BF∥MN∥PQ,
∴∠NCB+∠CBF=180°,∠FBD=∠BDP,
∵AC⊥BC,∴∠NCB=90°,
∴∠CBF=180°-90°=90°,∴∠ABC+∠ABF=90°,
∵BD⊥AB,∴∠ABF+∠DBF=90°,
∴∠ABC=∠FBD,∴∠ABC=∠BDP.
(3)任选1个解答即可.
选择A:∠ABC=15°.详解:
如图,过点B作BF∥MN,
设∠ABC=x,则∠EBF=∠AEB=2x,
由(2)可得∠BDP=∠ABC=x,∴∠DBF=x.
∠EBD=∠EBF+∠DBF=3x.
∵BE平分∠ABD,∴∠ABD=6x,
∵AB⊥BD,∴∠ABD=90°,
∴6x=90°,解得x=15°,∴∠ABC=15°.
选择B:∠ABC=30°.详解:设∠ABC=x,
∵BC⊥AC,MN∥PQ,∴BC⊥PQ,
∴∠QDB+∠DBC=90°,
∵AB⊥BD,∴∠ABD=90°,
∴∠ABC+∠DBC=90°,∴∠ABC=∠QDB=x,
∴∠BDP=180°-x,
∵BE平分∠ABD,∴∠ABE=∠DBE=45°,
在△ABC中,∠CAB=90°-x,
在△ABE中,∠AEB=180°-∠ABE-∠CAB=180°-45°-(90°-x)=45°+x,
∵∠BDP=2∠BEN,
∴180°-x=2(45°+x),解得x=30°,∴∠ABC=30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学七年级下册
第9章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.下列说法中,正确的是( )
A.两条不相交的直线叫做平行线
B.一条直线的平行线有且只有一条
C.若直线a∥b,a∥c,则b∥c
D.若两条线段不相交,则它们互相平行
2.【跨学科·物理】(2023四川凉山州中考)光线在不同介质中的传播速度是不同的,因此光线从水中射向空气中时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,两平行光线从水中射入空气中,∠1=45°,∠2=120°,则∠3+∠4=( )
A.165° B.155° C.105° D.90°
3.(2022山东泰安肥城期末)如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
4.(2023湖南邵阳中考)如图,直线a,b被直线c所截,已知a∥b,∠1=50°,则∠2的大小为( )
A.40° B.50° C.70° D.130°
5.(2023辽宁大连中考)如图,直线AB∥CD,∠ABE=45°,∠D=20°,则
∠E的度数为( )
A.20° B.25° C.30° D.35°
6.【长方形折叠问题】(2023山东临沂临沭期中)如图,将一张长方形纸条ABCD沿EF折叠,点B,A分别落在B',A'位置上,FB'与AD的交点为G.若∠DGF=110°,则∠FEG的度数为( )
A.40° B.45° C.50° D.55°
7.(2023山东济南莱芜期中)如图,AB∥CD,AD⊥AC,∠BAD=35°,则
∠ACD=( )
A.35° B.45° C.55° D.65°
8.(2021内蒙古包头中考)如图,直线l1∥l2,直线l3交l1于点A,交l2于点B,过点B的直线l4交l1于点C.若∠3=50°,∠1+∠2+∠3=240°,则
∠4等于( )
A.80° B.70° C.60° D.50°
9.(2023湖北宜昌中考)如图,小颖按如下方式操作直尺和含30°角的三角尺,依次画出了直线a,b,c.如果∠1=70°,则∠2的度数为( )
A.110° B.70°
C.40° D.30°
10.(2023湖北荆州中考)如图所示的“箭头”图形中,AB∥CD,∠B=
∠D=80°,∠E=∠F=47°,则图中∠G的度数是( )
A.80° B.76°
C.66° D.56°
11.如果两个角的两边分别平行,且其中一个角的度数比另一个角的度数的4倍少30°,那么这两个角的度数分别是( )
A.42°、138°
B.10°、10°
C.42°、138°或42°、10°
D.10°、10°或42°、138°
12.【平行线拐点模型】如图,AB∥EF,∠C=90°,则∠α、∠β、∠γ的关系是( )
A.∠β+∠γ-∠α=90°
B.∠α+∠β+∠γ=180°
C.∠α+∠β-∠γ=90°
D.∠β=∠α+∠γ
二、填空题(每小题3分,共18分)
13.在同一平面内有三条直线,如果其中有且只有两条直线相互平行,那么这三条直线有且只有 个交点.
14.(2023湖南永州中考)如图,AB∥CD,BC∥ED,∠B=80°,则∠D= 度.
15.【新考法】(2022山东济南二十八中期中)如图,点A,B,C,D在同一条直线上,若满足条件 ,则有AE∥BF.(要求:不再添加辅助线,只需填一个答案即可)
16.(2023浙江杭州中考)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,点F在线段BC的延长线上.若∠ADE=28°,∠ACF=118°,则∠A= °.
17.(2023内蒙古通辽中考)将一副三角尺按如图所示的方式放置,其中AB∥DE,则∠CDF= 度.
18.两条平行直线被第三条直线所截,有下列结论:
①一对同位角的平分线互相平行;
②一对内错角的平分线互相平行;
③一对同旁内角的平分线互相平行;
④一对同旁内角的平分线互相垂直.
其中结论正确的是 .(填序号)
三、解答题(共46分)
19.(2023山东青岛二十六中期末)(6分)如图,已知CD是∠ACB的平分线,∠A=70°,∠B=60°,DE∥BC.求∠EDC的度数.
20.(6分)如图,直线CD与直线 AB 相交于点C.
(1)根据下列语句画图:
①过点P作PQ∥CD,交AB于点Q.
②过点P作PR⊥CD,垂足为R.
(2)若∠DCB=120°,猜想∠PQC的度数,并说明理由.
21.(2023山东济南济阳期中)(7分)如图,AB∥CD,CE平分∠DCB,
∠E=∠3.求证:DE∥BC.
22.(2023山东青岛黄岛期中)(8分)如图,已知∠ADE=∠BFG,∠BAC+∠AED=180°.
(1)∠BAC与哪个角相等 为什么
(2)试判断AD与FG有怎样的位置关系,请说明理由.
(3)若AD⊥BC,∠BFG=30°,求∠B的度数.
23.(8分)如图,把一张长方形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF应为多少度,才能使AB'∥BD
24.(2023山东青岛市南期中)(11分)已知直线MN∥PQ,点A在直线MN上,点B,C为平面内两点,AC⊥BC于点C.
(1)如图1,当点B在直线MN上,点C在直线MN上方时,延长CB交直线PQ于点D,则∠CAB和∠CDP之间的数量关系是 .
(2)如图2,当点C在直线MN上且在点A左侧,点B在直线MN与PQ之间时,过点B作BD⊥AB交直线PQ于点D.为探究∠ABC与∠BDP之间的数量关系,小明过点B作BF∥MN,请根据他的思路,写出∠ABC与∠BDP的关系,并说明理由.
(3)请从下面A,B两题中任选一题作答.
A.如图3,在(2)的条件下,作∠ABD的平分线交直线MN于点E,当∠AEB=2∠ABC时,直接写出∠ABC的度数.
B.如图4,当点C在直线MN上且在点A左侧,点B在直线PQ下方时,过点B作BD⊥AB交直线PQ于点D,作∠ABD的平分线交直线MN于点E,当∠BDP=2∠BEN时,直接写出∠ABC的度数.
答案全解全析
1.C 在同一平面内,两条不相交的直线叫做平行线,故A错误;过直线外一点,有且只有一条直线与已知直线平行,而一条直线的平行线有无数条,故B错误;平行于同一直线的两条直线平行,故C正确;根据平行线的定义可知D是错误的.故选C.
2.C ∵在水中平行的光线,在空气中也是平行的,∠1=45°,∠2=120°,题图中两光线平行,
∴∠3=∠1=45°,
∵水面与杯底面平行,∴∠4=180°-∠2=60°,
∴∠3+∠4=105°.故选C.
3.C ①∠1与∠4不是内错角,原说法错误;②∠1与∠2是同位角,原说法正确;③∠2与∠4不是内错角,原说法错误;④∠4与∠5是同旁内角,原说法正确;⑤∠2与∠4不是同位角,原说法错误;⑥∠2与∠5是内错角,原说法正确.正确的有3个.故选C.
4.B 如图所示:
∵a∥b,∴∠2=∠3,
∵∠1=∠3,∠1=50°,∴∠1=∠2=50°.故选B.
5.B ∵AB∥CD,∴∠ABE=∠BCD=45°,∴∠DCE=135°.
∴∠E=180°-∠DCE-∠D=180°-135°-20°=25°.故选B.
6.D 由题意知AD∥BC,∴∠BFG=∠DGF=110°.
由折叠的性质可知∠BFE=∠EFG=∠BFG=55°,
∵AD∥BC,∴∠FEG=∠BFE=55°.故选D.
方法解读 长方形折叠问题的解题步骤如下:
第一步:还原;第二步:标出所有相等的角;第三步:找内错角(相等)、同位角(相等)和同旁内角(互补);第四步:计算.
7.C ∵AD⊥AC,∴∠CAD=90°,
∵AB∥CD,∴∠DCA+∠CAB=180°,
又∵∠BAD=35°,
∴∠ACD=180°-∠CAD-∠BAD=55°,故选C.
8.B 如图,
因为l1∥l2,所以∠1+∠3=180°,
因为∠1+∠2+∠3=240°,
所以∠2=240°-(∠1+∠3)=60°.
因为∠3+∠2+∠5=180°,∠3=50°,
所以∠5=180°-∠2-∠3=70°,
因为l1∥l2,所以∠4=∠5=70°,故选B.
9.C 如图,由题意得∠4=30°,b∥c,
∴∠3=∠1=70°,∴∠6=110°.
∵∠4+∠5+∠6=180°,∴∠4+∠5=70°,∴∠5=40°,
∴∠2=∠5=40°,故选C.
10.C 如图,延长AB交EG于M,延长CD交FG于N,过G作GK∥AB,
∵AB∥CD,∴GK∥AB∥CD,
∴∠KGM=∠EMB,∠KGN=∠DNF,
∴∠KGM+∠KGN=∠EMB+∠DNF,
∴∠EGF=∠EMB+∠DNF,
∵∠ABE=80°,∴∠EBM=100°,∵∠E=47°,
∴∠EMB=180°-∠MBE-∠E=33°,
同理:∠DNF=33°,
∴∠EGF=∠EMB+∠DNF=33°+33°=66°.故选C.
11.D 设其中一个角的度数为x°,则另一个角的度数为(4x-30)°,
分两种情况:(1)若两个角的度数相等,则x=4x-30,解得x=10,则4x-30=4×10-30=10;
(2)若两个角互补,则x+(4x-30)=180,解得x=42,则4x-30=4×42-30=138.
故这两个角的度数分别是10°、10°或42°、138°.
故选D.
12.C 如图,分别过点C、D作CM∥AB,DN∥AB,
因为AB∥EF,所以AB∥CM∥ND∥EF,
所以∠1=∠α,∠2=∠3,∠4=∠γ.
由图知∠1+∠2=∠BCD=90°,∠3+∠4=∠β,
所以∠α+∠2=90°,∠3+∠γ=∠β,
即∠2=90°-∠α,∠3=∠β-∠γ,
所以90°-∠α=∠β-∠γ,即∠α+∠β-∠γ=90°.
方法解读 平行线拐点模型:
①辅助线:过拐点作平行线,且有多少个拐点就作多少条平行线;②所有朝左的角的度数之和等于所有朝右的角的度数之和.
13.2
解析 在同一平面内有三条直线,如果其中有且只有两条直线相互平行,那么第三条直线与这两条平行直线分别相交,所以这三条直线有且只有2个交点.
14.100
解析 ∵AB∥CD,∠B=80°,∴∠BCD=∠B=80°,
∵BC∥ED,∴∠D+∠BCD=180°,∴∠D=100°.
15.∠5=∠A(答案不唯一)
解析 添加∠5=∠A,可根据“同位角相等,两直线平行”判定AE∥BF.(答案不唯一)
16.90
解析 ∵DE∥BC,∴∠B=∠ADE=28°,
∵∠ACF=118°,∴∠ACB=62°.∵∠A+∠B+∠ACB=180°,
∴∠A+∠B=118°,
∴∠A=118°-∠B=118°-28°=90°.
17.105
解析 ∵AB∥DE,∴∠BDE=∠B=30°,
∴∠CDF=180°-∠EDF-∠BDE=180°-45°-30°=105°.
18.①②④
解析 ①两直线平行,同位角相等,其角平分线分得的角也相等,根据同位角相等,两直线平行可判定一对同位角的平分线互相平行;②两直线平行,内错角相等,其角平分线分得的角也相等,根据内错角相等,两直线平行可判定一对内错角的平分线互相平行;③显然不对;④两直线平行,同旁内角互补,其角平分线分得的不同的两角互余,从而推出一对同旁内角的平分线互相垂直.
综上,结论正确的是①②④.
19.解析 ∵CD是∠ACB的平分线,
∴∠DCB=∠ACB,
∵DE∥BC,∴∠EDC=∠DCB,∴∠EDC=∠ACB,
∵∠A=70°,∠B=60°,∴∠ACB=180°-(∠A+∠B)=180°-(70°+60°)=50°,
∴∠EDC=∠ACB=×50°=25°,
∴∠EDC的度数为25°.
20.解析 (1)①如图所示,PQ即为所求.
②如图所示,PR即为所求.
(2)∠PQC=60°.理由如下:
因为PQ∥CD,所以∠DCB+∠PQC=180°,
因为∠DCB=120°,
所以∠PQC=180°-∠DCB=180°-120°=60°.
21.证明 ∵AB∥CD,∴∠3=∠2,
∵∠E=∠3,∴∠2=∠E,
∵CE平分∠DCB,∴∠1=∠2=∠BCD,
∴∠E=∠1,∴DE∥BC.
22.解析 (1)∠BAC=∠CED.理由如下:
∵∠BAC+∠AED=180°,∠CED+∠AED=180°,
∴∠BAC=∠CED(同角的补角相等).
(2)AD∥FG.理由如下:
∵∠BAC=∠CED,∴AB∥DE,∴∠BAD=∠ADE,
∵∠ADE=∠BFG,∴∠BFG=∠BAD,∴AD∥FG.
(3)∵AD⊥BC,AD∥FG,∴FG⊥BC,
∴∠FGB=90°,∴∠B+∠BFG=90°,
∵∠BFG=30°,∴∠B=60°.
23.解析 ∠BAF应为55°.理由如下:
因为四边形ABCD是长方形,
所以AD∥BC,∠ABC=90°,
因为∠ADB=20°,所以∠DBC=∠ADB=20°,
所以∠ABD=70°.
要使AB'∥BD,需使∠ABD+∠BAB'=180°,
即∠BAB'=110°,
由折叠的性质知∠BAF=∠B'AF,
所以∠BAF=∠BAB'=55°.
24.解析 (1)∵AC⊥BC,∴∠CAB+∠CBA=90°,
∵MN∥PQ,∴∠CBA=∠CDP,∴∠CAB+∠CDP=90°,
故答案为∠CAB+∠CDP=90°.
(2)∠ABC=∠BDP,理由如下:
∵BF∥MN,MN∥PQ,∴BF∥MN∥PQ,
∴∠NCB+∠CBF=180°,∠FBD=∠BDP,
∵AC⊥BC,∴∠NCB=90°,
∴∠CBF=180°-90°=90°,∴∠ABC+∠ABF=90°,
∵BD⊥AB,∴∠ABF+∠DBF=90°,
∴∠ABC=∠FBD,∴∠ABC=∠BDP.
(3)任选1个解答即可.
选择A:∠ABC=15°.详解:
如图,过点B作BF∥MN,
设∠ABC=x,则∠EBF=∠AEB=2x,
由(2)可得∠BDP=∠ABC=x,∴∠DBF=x.
∠EBD=∠EBF+∠DBF=3x.
∵BE平分∠ABD,∴∠ABD=6x,
∵AB⊥BD,∴∠ABD=90°,
∴6x=90°,解得x=15°,∴∠ABC=15°.
选择B:∠ABC=30°.详解:设∠ABC=x,
∵BC⊥AC,MN∥PQ,∴BC⊥PQ,
∴∠QDB+∠DBC=90°,
∵AB⊥BD,∴∠ABD=90°,
∴∠ABC+∠DBC=90°,∴∠ABC=∠QDB=x,
∴∠BDP=180°-x,
∵BE平分∠ABD,∴∠ABE=∠DBE=45°,
在△ABC中,∠CAB=90°-x,
在△ABE中,∠AEB=180°-∠ABE-∠CAB=180°-45°-(90°-x)=45°+x,
∵∠BDP=2∠BEN,
∴180°-x=2(45°+x),解得x=30°,∴∠ABC=30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
