2024青岛版数学七年级下册--专项素养综合全练(二)平行线中与学具或折叠有关的问题(含解析)
文档属性
| 名称 | 2024青岛版数学七年级下册--专项素养综合全练(二)平行线中与学具或折叠有关的问题(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 381.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:35 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024青岛版数学七年级下册
专项素养综合全练(二)
平行线中与学具或折叠有关的问题
类型一 三角尺与直尺组合
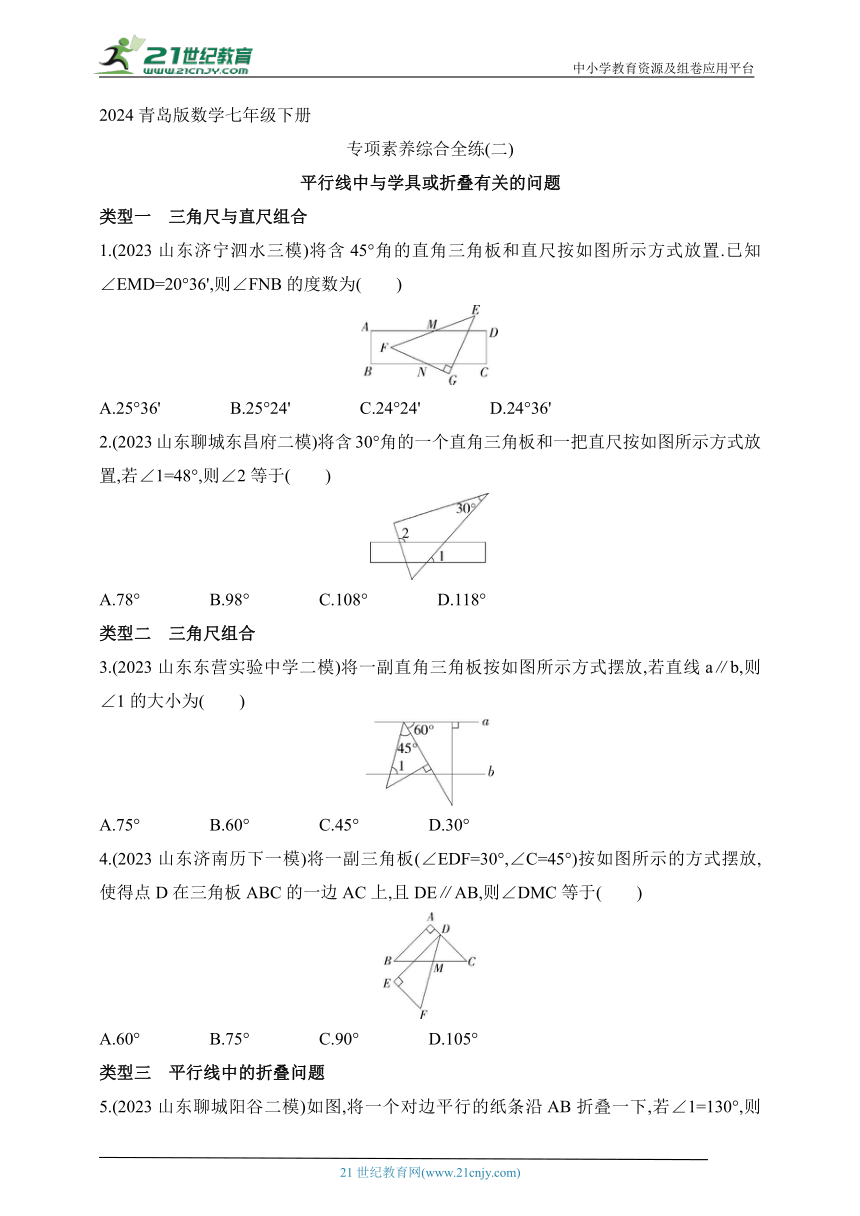
1.(2023山东济宁泗水三模)将含45°角的直角三角板和直尺按如图所示方式放置.已知∠EMD=20°36',则∠FNB的度数为( )
A.25°36' B.25°24' C.24°24' D.24°36'
2.(2023山东聊城东昌府二模)将含30°角的一个直角三角板和一把直尺按如图所示方式放置,若∠1=48°,则∠2等于( )
A.78° B.98° C.108° D.118°
类型二 三角尺组合
3.(2023山东东营实验中学二模)将一副直角三角板按如图所示方式摆放,若直线a∥b,则∠1的大小为( )
A.75° B.60° C.45° D.30°
4.(2023山东济南历下一模)将一副三角板(∠EDF=30°,∠C=45°)按如图所示的方式摆放,使得点D在三角板ABC的一边AC上,且DE∥AB,则∠DMC等于( )
A.60° B.75° C.90° D.105°
类型三 平行线中的折叠问题
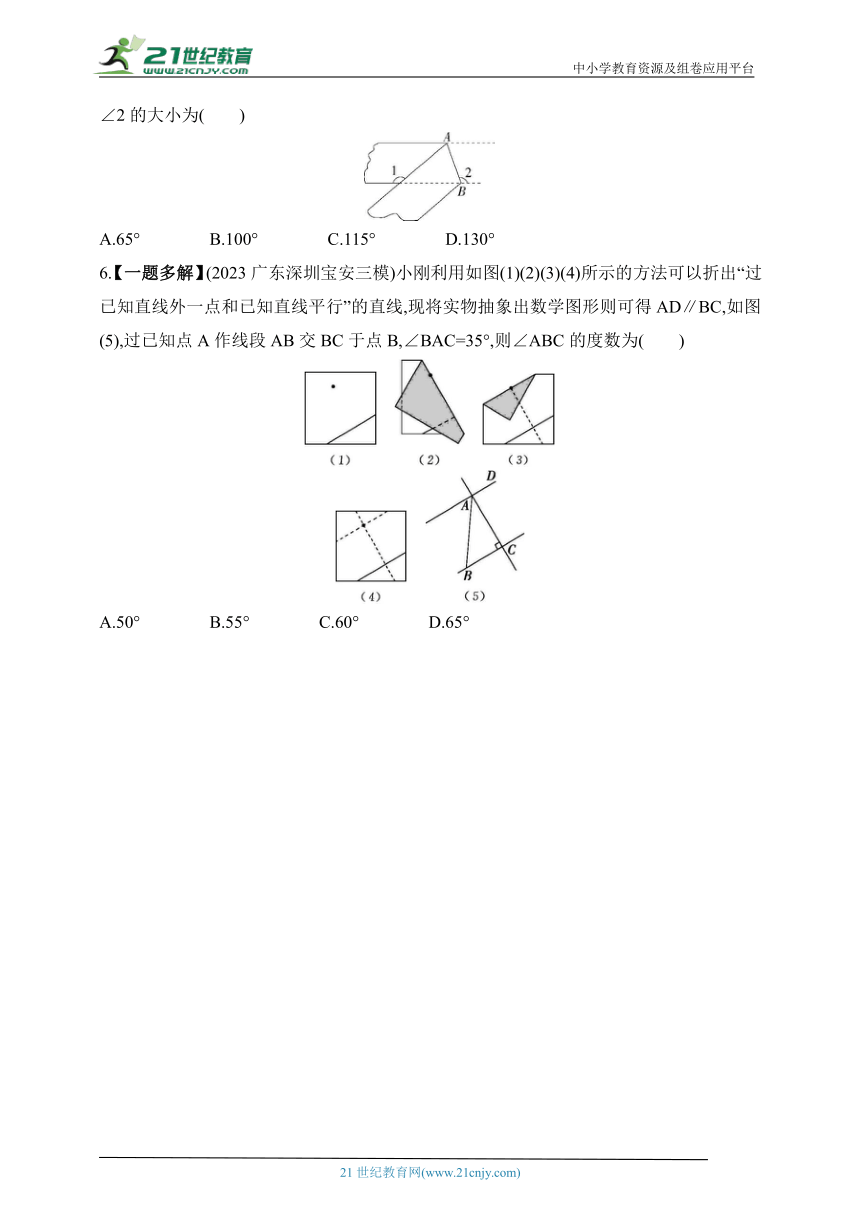
5.(2023山东聊城阳谷二模)如图,将一个对边平行的纸条沿AB折叠一下,若∠1=130°,则∠2的大小为( )
A.65° B.100° C.115° D.130°
6.【一题多解】(2023广东深圳宝安三模)小刚利用如图(1)(2)(3)(4)所示的方法可以折出“过已知直线外一点和已知直线平行”的直线,现将实物抽象出数学图形则可得AD∥BC,如图(5),过已知点A作线段AB交BC于点B,∠BAC=35°,则∠ABC的度数为( )
A.50° B.55° C.60° D.65°
答案全解全析
1.C 如图所示,过点F作FH∥AD,
∵AD∥BC,∴FH∥AD∥BC,
∴∠EFH=∠EMD=20°36',∠FNB=∠GFH,
又∵∠EFG=45°,
∴∠FNB=∠GFH=∠EFG-∠EFH=24°24'.
故选C.
2.C 如图,∵∠1=48°,
∴由平行线的性质得∠3=∠1=48°,
依题意可知∠4=60°,∴∠5=180°-∠3-∠4=72°,
∴∠2=180°-∠5=180°-72°=108°.故选C.
3.A ∵a∥b,∴∠1+45°+60°=180°,
∴∠1=75°.故选A.
4.B 如图,
∵DE∥AB,∴∠1=∠B=45°,
∵∠EDF=30°,∴∠DMB=180°-∠EDF-∠1=105°,
∴∠DMC=180°-∠DMB=75°,故选B.
5.C 如图:
将一个对边平行的纸条沿AB折叠一下,
则2∠3=∠1,∠2+∠3=180°,
∵∠1=130°,∴∠3=∠1=65°,
∴∠2=180°-∠3=180°-65°=115°.故选C.
6.B 解法一:由题意得∠CAD=90°,
∴∠BAD=∠CAD+∠BAC=125°,
∵AD∥BC,∴∠ABC=180°-∠BAD=55°,故选B.
解法二:∵∠ACB=90°,∠BAC=35°,
∴∠ABC=180°-∠ACB-∠BAC=180°-90°-35°=55°.故选B.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学七年级下册
专项素养综合全练(二)
平行线中与学具或折叠有关的问题
类型一 三角尺与直尺组合
1.(2023山东济宁泗水三模)将含45°角的直角三角板和直尺按如图所示方式放置.已知∠EMD=20°36',则∠FNB的度数为( )
A.25°36' B.25°24' C.24°24' D.24°36'
2.(2023山东聊城东昌府二模)将含30°角的一个直角三角板和一把直尺按如图所示方式放置,若∠1=48°,则∠2等于( )
A.78° B.98° C.108° D.118°
类型二 三角尺组合
3.(2023山东东营实验中学二模)将一副直角三角板按如图所示方式摆放,若直线a∥b,则∠1的大小为( )
A.75° B.60° C.45° D.30°
4.(2023山东济南历下一模)将一副三角板(∠EDF=30°,∠C=45°)按如图所示的方式摆放,使得点D在三角板ABC的一边AC上,且DE∥AB,则∠DMC等于( )
A.60° B.75° C.90° D.105°
类型三 平行线中的折叠问题
5.(2023山东聊城阳谷二模)如图,将一个对边平行的纸条沿AB折叠一下,若∠1=130°,则∠2的大小为( )
A.65° B.100° C.115° D.130°
6.【一题多解】(2023广东深圳宝安三模)小刚利用如图(1)(2)(3)(4)所示的方法可以折出“过已知直线外一点和已知直线平行”的直线,现将实物抽象出数学图形则可得AD∥BC,如图(5),过已知点A作线段AB交BC于点B,∠BAC=35°,则∠ABC的度数为( )
A.50° B.55° C.60° D.65°
答案全解全析
1.C 如图所示,过点F作FH∥AD,
∵AD∥BC,∴FH∥AD∥BC,
∴∠EFH=∠EMD=20°36',∠FNB=∠GFH,
又∵∠EFG=45°,
∴∠FNB=∠GFH=∠EFG-∠EFH=24°24'.
故选C.
2.C 如图,∵∠1=48°,
∴由平行线的性质得∠3=∠1=48°,
依题意可知∠4=60°,∴∠5=180°-∠3-∠4=72°,
∴∠2=180°-∠5=180°-72°=108°.故选C.
3.A ∵a∥b,∴∠1+45°+60°=180°,
∴∠1=75°.故选A.
4.B 如图,
∵DE∥AB,∴∠1=∠B=45°,
∵∠EDF=30°,∴∠DMB=180°-∠EDF-∠1=105°,
∴∠DMC=180°-∠DMB=75°,故选B.
5.C 如图:
将一个对边平行的纸条沿AB折叠一下,
则2∠3=∠1,∠2+∠3=180°,
∵∠1=130°,∴∠3=∠1=65°,
∴∠2=180°-∠3=180°-65°=115°.故选C.
6.B 解法一:由题意得∠CAD=90°,
∴∠BAD=∠CAD+∠BAC=125°,
∵AD∥BC,∴∠ABC=180°-∠BAD=55°,故选B.
解法二:∵∠ACB=90°,∠BAC=35°,
∴∠ABC=180°-∠ACB-∠BAC=180°-90°-35°=55°.故选B.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
