2024青岛版数学七年级下册--专项素养综合全练(七)新定义型试题(含解析)
文档属性
| 名称 | 2024青岛版数学七年级下册--专项素养综合全练(七)新定义型试题(含解析) | 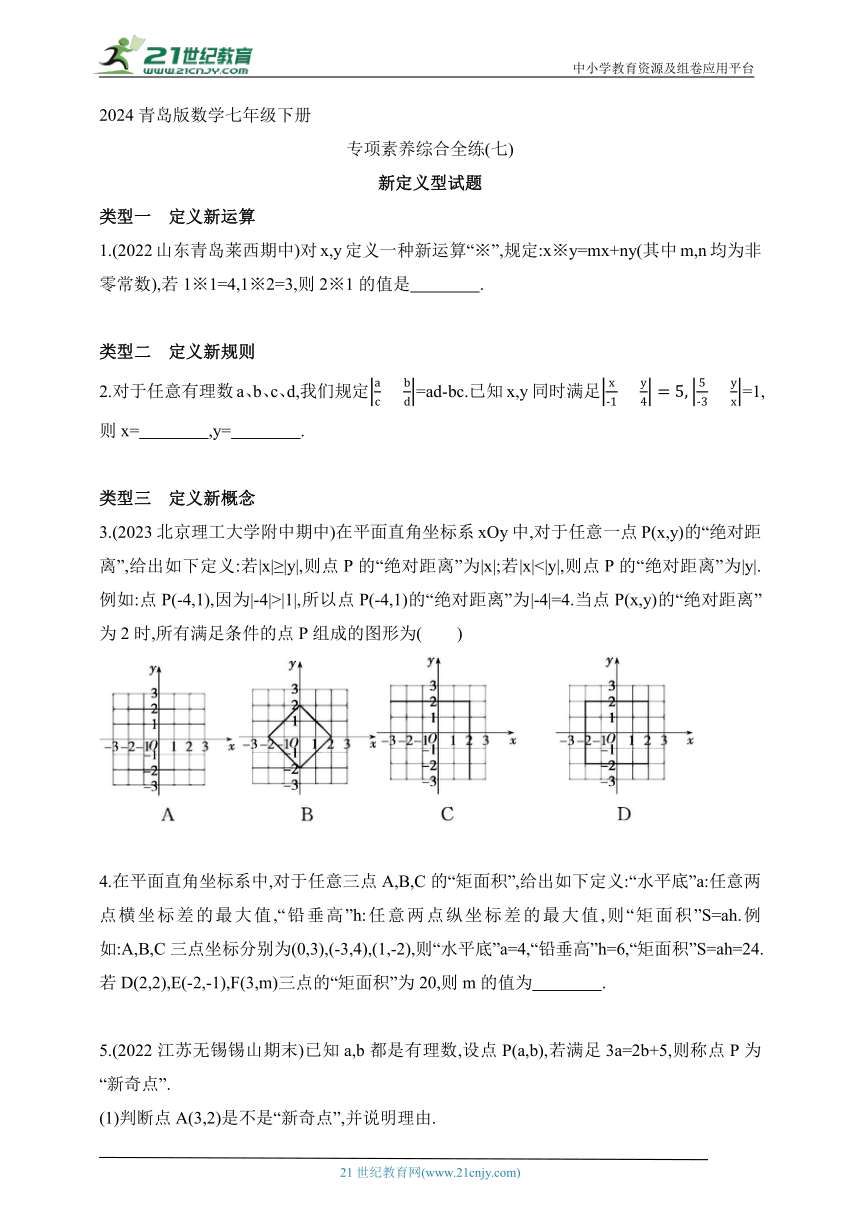 | |
| 格式 | docx | ||
| 文件大小 | 352.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024青岛版数学七年级下册
专项素养综合全练(七)
新定义型试题
类型一 定义新运算
1.(2022山东青岛莱西期中)对x,y定义一种新运算“※”,规定:x※y=mx+ny(其中m,n均为非零常数),若1※1=4,1※2=3,则2※1的值是 .
类型二 定义新规则
2.对于任意有理数a、b、c、d,我们规定=ad-bc.已知x,y同时满足=1,则x= ,y= .
类型三 定义新概念
3.(2023北京理工大学附中期中)在平面直角坐标系xOy中,对于任意一点P(x,y)的“绝对距离”,给出如下定义:若|x|≥|y|,则点P的“绝对距离”为|x|;若|x|<|y|,则点P的“绝对距离”为|y|.例如:点P(-4,1),因为|-4|>|1|,所以点P(-4,1)的“绝对距离”为|-4|=4.当点P(x,y)的“绝对距离”为2时,所有满足条件的点P组成的图形为( )
4.在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:A,B,C三点坐标分别为(0,3),(-3,4),(1,-2),则“水平底”a=4,“铅垂高”h=6,“矩面积”S=ah=24.若D(2,2),E(-2,-1),F(3,m)三点的“矩面积”为20,则m的值为 .
5.(2022江苏无锡锡山期末)已知a,b都是有理数,设点P(a,b),若满足3a=2b+5,则称点P为“新奇点”.
(1)判断点A(3,2)是不是“新奇点”,并说明理由.
(2)若点M(m-1,3m+2)是“新奇点”,请判断点M在第几象限,并说明理由.
答案全解全析
1.9
解析 ∵1※1=4,1※2=3,
∴则x※y=5x-y.
∴2※1=2×5-1=9.
2.2;-3
解析 根据题中的新定义得
①×3-②得7x=14,
解得x=2,
把x=2代入①得8+y=5,
解得y=-3.
3.D ∵点P(x,y)的“绝对距离”为2,
∴|x|=2,|y|≤2或|y|=2,|x|<2,
即x=2时,-2≤y≤2,x=-2时,-2≤y≤2,y=2时,-2即可确定点P组成的图形为D选项中的正方形,故选D.
4.3或-2
解析 ∵D(2,2),E(-2,-1),F(3,m),
∴“水平底”a=3-(-2)=5,
“铅垂高”h=3或|1+m|或|2-m|.
①当h=3时,三点的“矩面积”S=5×3=15≠20,不合题意;
②当h=|1+m|时,三点的“矩面积”S=5×|1+m|=20,
解得m=3或m=-5(舍去);
③当h=|2-m|时,三点的“矩面积”S=5×|2-m|=20,
解得m=-2或m=6(舍去).
综上,m=3或-2.
5.解析 (1)点A(3,2)是“新奇点”.理由如下:
∵3×3=2×2+5,∴点A(3,2)是“新奇点”.
(2)点M在第三象限.理由如下:
∵点M(m-1,3m+2)是“新奇点”,
∴3(m-1)=2(3m+2)+5,解得m=-4,
∴m-1=-5,3m+2=-10,
∴点M在第三象限.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学七年级下册
专项素养综合全练(七)
新定义型试题
类型一 定义新运算
1.(2022山东青岛莱西期中)对x,y定义一种新运算“※”,规定:x※y=mx+ny(其中m,n均为非零常数),若1※1=4,1※2=3,则2※1的值是 .
类型二 定义新规则
2.对于任意有理数a、b、c、d,我们规定=ad-bc.已知x,y同时满足=1,则x= ,y= .
类型三 定义新概念
3.(2023北京理工大学附中期中)在平面直角坐标系xOy中,对于任意一点P(x,y)的“绝对距离”,给出如下定义:若|x|≥|y|,则点P的“绝对距离”为|x|;若|x|<|y|,则点P的“绝对距离”为|y|.例如:点P(-4,1),因为|-4|>|1|,所以点P(-4,1)的“绝对距离”为|-4|=4.当点P(x,y)的“绝对距离”为2时,所有满足条件的点P组成的图形为( )
4.在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:A,B,C三点坐标分别为(0,3),(-3,4),(1,-2),则“水平底”a=4,“铅垂高”h=6,“矩面积”S=ah=24.若D(2,2),E(-2,-1),F(3,m)三点的“矩面积”为20,则m的值为 .
5.(2022江苏无锡锡山期末)已知a,b都是有理数,设点P(a,b),若满足3a=2b+5,则称点P为“新奇点”.
(1)判断点A(3,2)是不是“新奇点”,并说明理由.
(2)若点M(m-1,3m+2)是“新奇点”,请判断点M在第几象限,并说明理由.
答案全解全析
1.9
解析 ∵1※1=4,1※2=3,
∴则x※y=5x-y.
∴2※1=2×5-1=9.
2.2;-3
解析 根据题中的新定义得
①×3-②得7x=14,
解得x=2,
把x=2代入①得8+y=5,
解得y=-3.
3.D ∵点P(x,y)的“绝对距离”为2,
∴|x|=2,|y|≤2或|y|=2,|x|<2,
即x=2时,-2≤y≤2,x=-2时,-2≤y≤2,y=2时,-2
4.3或-2
解析 ∵D(2,2),E(-2,-1),F(3,m),
∴“水平底”a=3-(-2)=5,
“铅垂高”h=3或|1+m|或|2-m|.
①当h=3时,三点的“矩面积”S=5×3=15≠20,不合题意;
②当h=|1+m|时,三点的“矩面积”S=5×|1+m|=20,
解得m=3或m=-5(舍去);
③当h=|2-m|时,三点的“矩面积”S=5×|2-m|=20,
解得m=-2或m=6(舍去).
综上,m=3或-2.
5.解析 (1)点A(3,2)是“新奇点”.理由如下:
∵3×3=2×2+5,∴点A(3,2)是“新奇点”.
(2)点M在第三象限.理由如下:
∵点M(m-1,3m+2)是“新奇点”,
∴3(m-1)=2(3m+2)+5,解得m=-4,
∴m-1=-5,3m+2=-10,
∴点M在第三象限.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
