2024苏科版数学七年级下册--第9章《整式乘法与因式分解》素养综合检测(含解析)
文档属性
| 名称 | 2024苏科版数学七年级下册--第9章《整式乘法与因式分解》素养综合检测(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 336.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024苏科版数学七年级下册
第9章 素养综合检测
(满分100分,限时60分钟)
一、选择题(本大题共8小题,每小题3分,共24分)
1.式子n2-1与n2+n的公因式是( )
A.n+1 B.n2 C.n D.n-1
2.(2023湖南长沙中考)下列计算正确的是( )
A.x2·x3=x5 B.(x3)3=x6 C.x(x+1)=x2+1 D.(2a-1)2=4a2-1
3.(2023江苏南京玄武期中)下列从左到右的变形是因式分解的是( )
A.ab+ac+d=a(b+c)+d
B.(a+1)(a-1)=a2-1
C.x2-2x+1=(x-1)2
D.a(a+1)=a2+a
4.若多项式x2+mx+4能用完全平方公式分解因式,则m的值是( )
A.2 B.-2 C.±4 D.±8
5.【新考向·代数推理】(2023河北中考)若k为任意整数,则(2k+3)2-4k2的值总能( )
A.被2整除 B.被3整除 C.被5整除 D.被7整除
6.我们所学的多项式因式分解的方法主要有①提公因式法;②平方差公式法;③完全平方公式法.现将多项式(x-y)3+4(y-x)进行因式分解,使用的方法有( )
A.①② B.①③ C.②③ D.①②③
7.【数形结合思想】如图,现有正方形A类、B类卡片和长方形C类卡片若干张,如果要拼成一个长为(a+3b),宽为(a+2b)的大长方形,则需要C类卡片( )
A.3张 B.4张
C.5张 D.6张
8.【新考向·新定义试题】在数学中,为了书写简便,数学家欧拉引进了求和符号“”.如:记k=1+2+3+…+(n-1)+n,(x+k)=(x+3)+(x+4)+…
+(x+n),已知[(x+k)(x-k+1)]=4x2+4x+m,则m的值是( )
A.40 B.-70 C.-40 D.-20
二、填空题(本大题共8小题,每小题3分,共24分)
9.三个连续奇数,中间的数是n,则它们的积是 .
10.如果单项式2x3y5与-4x4y2的积为mx7yn ,那么mn= .
11.观察等式:①9-1=2×4;②25-1=4×6;③49-1=6×8;……按照这种规律写出第n个等式: .
12.(2023江苏南京玄武期中)已知a-b=1,则a2-b2-2b的值为 .
13.如果x-a与x-b的乘积中不含x的一次项,那么a与b的关系为 .
14.【新考向·新定义试题】(2020浙江衢州中考)定义a※b=a(b+1),例如:2※3=2×(3+1)=2×4=8,则(x-1)※x的结果为 .
15.若关于x的三次四项式x3+ax2+bx+3能分解成(x+1)(x2-2x+3),则a+b= .
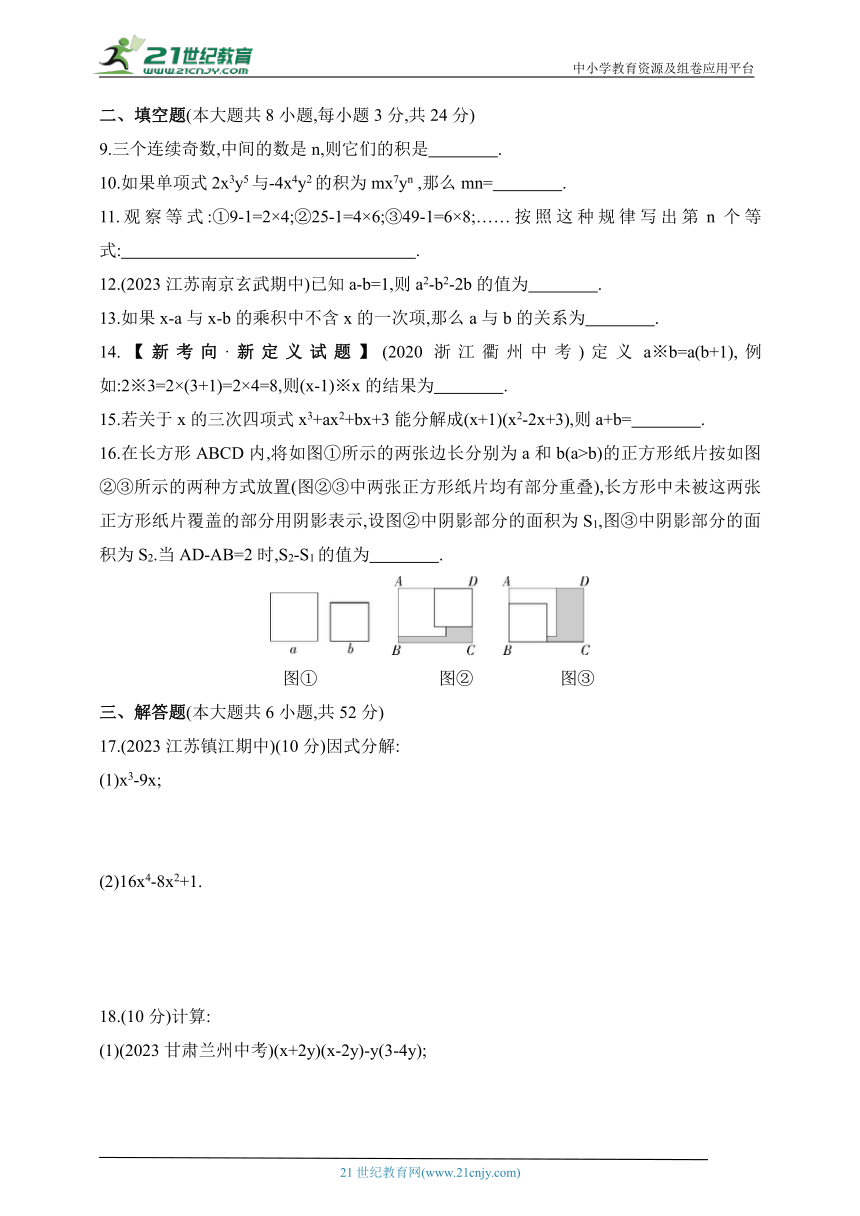
16.在长方形ABCD内,将如图①所示的两张边长分别为a和b(a>b)的正方形纸片按如图②③所示的两种方式放置(图②③中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图②中阴影部分的面积为S1,图③中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为 .
图① 图② 图③
三、解答题(本大题共6小题,共52分)
17.(2023江苏镇江期中)(10分)因式分解:
(1)x3-9x;
(2)16x4-8x2+1.
18.(10分)计算:
(1)(2023甘肃兰州中考)(x+2y)(x-2y)-y(3-4y);
(2)(2023山西中考)x(x+2)+(x+1)2-4x.
19.【新考向·过程性学习试题】(6分)阅读例题的解答过程,并解答(1)(2)中的问题.
例:计算(a-2b+3)(a+2b-3).
原式=[a-(2b-3)][a+(2b-3)]①
=a2-(2b-3)2②
=a2-(4b2-12b+9)③
=a2-4b2+12b-9.
(1)例题求解过程中,利用了整体思想,其中①→②的运算依据是 ,②→③的运算依据是 ;(填整式乘法公式的名称)
(2)用此方法计算:(a+2x-y-b)(a-2x+y-b).
20.(8分)先化简,再求值:(a-3b)(a+3b)+(a-3b)2,其中a=-3,b=.
21.(8分)若x满足(5-x)(x-2)=2,求(x-5)2+(2-x)2的值.
解:设5-x=a,x-2=b,则(5-x)(x-2)=ab=2,a+b=(5-x)+(x-2)=3,
∴(x-5)2+(2-x)2=(5-x)2+(x-2)2=a2+b2=(a+b)2-2ab=32-2×2=5.
请运用上面的方法求解下面的问题:
(1)若x满足(8-x)(x-2)=5,求(8-x)2+(x-2)2的值;
(2)如图,已知正方形ABCD的边长为x,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是35,求长方形EMFD的周长.
22.(10分)把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图②,可得等式: .
(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图③,将边长分别为a、b的两个正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若这两个正方形的边长a、b满足a+b=10,ab=20,请求出阴影部分的面积.
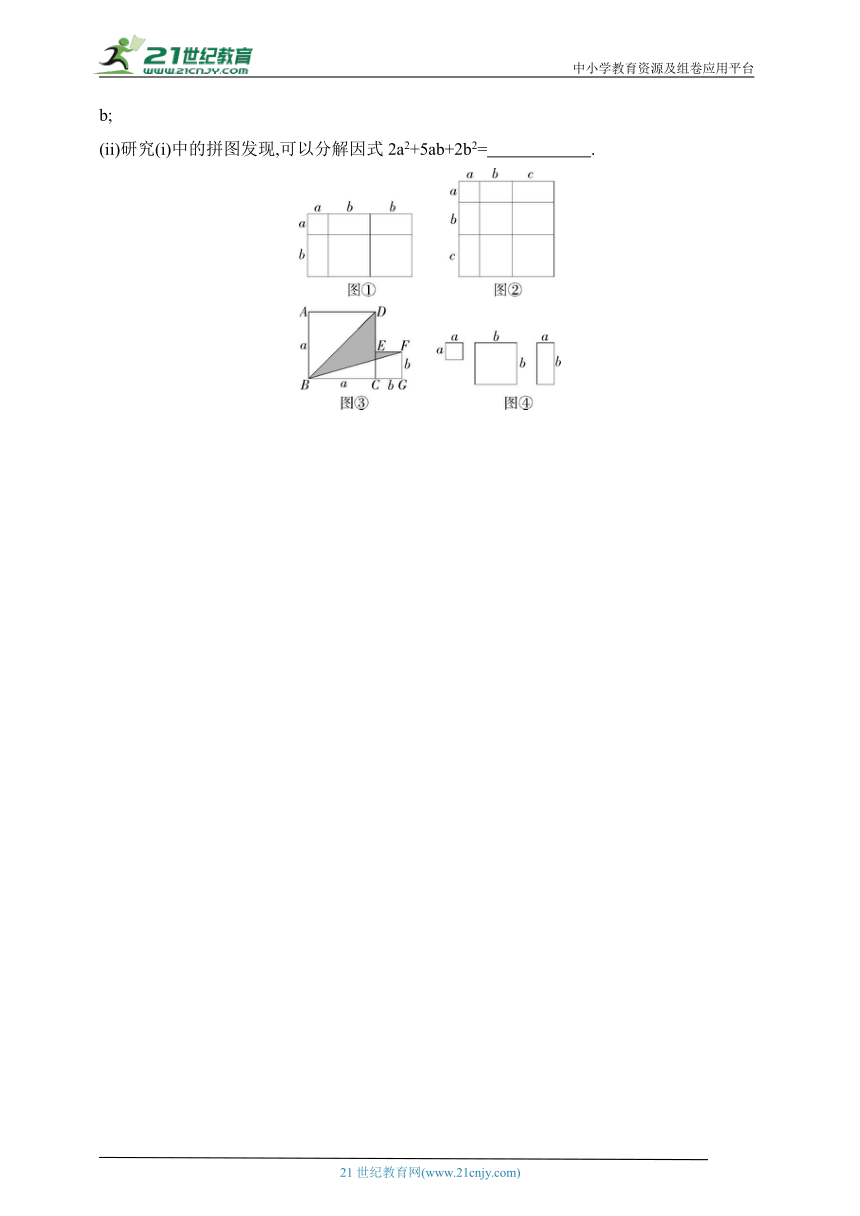
(4)图④中给出了边长分别为a、b的小正方形纸片和邻边长分别为a、b的长方形纸片,现有足量的这三种纸片.
(i)请用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,并仿照图①②画出拼法并标注a、b;
(ii)研究(i)中的拼图发现,可以分解因式2a2+5ab+2b2= .
答案全解全析
1.A ∵n2-1=(n+1)(n-1),n2+n=n(n+1),∴n2-1与n2+n的公因式是n+1.故选A.
2.A A.x2·x3=x5,本选项符合题意;
B.(x3)3=x9≠x6,本选项不符合题意;
C.x(x+1)=x2+x,本选项不符合题意;
D.(2a-1)2=4a2-4a+1≠4a2-1,本选项不符合题意.故选A.
3.C A.ab+ac+d=a(b+c)+d,右边不是几个整式的积的形式,不属于因式分解,故此选项不符合题意;
B.(a+1)(a-1)=a2-1,是整式的乘法,不属于因式分解,故此选项不符合题意;
C.x2-2x+1=(x-1)2,右边是几个整式的积的形式,属于因式分解,故此选项符合题意;
D.a(a+1)=a2+a,是整式的乘法,不属于因式分解,故此选项不符合题意.
故选C.
4.C 当m=4时,x2+4x+4=(x+2)2,当m=-4时,x2-4x+4=(x-2)2,所以m=±4.故选C.
5.B (2k+3)2-4k2=4k2+12k+9-4k2=12k+9=3(4k+3),
∵k为任意整数,
∴(2k+3)2-4k2的值总能被3整除,故选B.
6.A (x-y)3+4(y-x)=(x-y)3-4(x-y)=(x-y)[(x-y)2-4]=(x-y)(x-y+2)(x-y-2),故将多项式(x-y)3+4(y-x)进行因式分解,使用的方法有①提公因式法,②平方差公式法.故选A.
7.C 因为(a+3b)(a+2b)=a2+2ab+3ab+6b2=a2+5ab+6b2,所以需要A类卡片1张、B类卡片6张、C类卡片5张.故选C.
8.C ∵x2项的系数是4,∴n=5,
∴(x+2)(x-1)+(x+3)(x-2)+(x+4)(x-3)+(x+5)(x-4)=(x2+x-2)+(x2+x-6)+(x2+x-12)+(x2+x-20)=4x2+4x-40.
∵[(x+k)(x-k+1)]=4x2+4x+m,∴m=-40.故选C.
9.答案 n3-4n
解析 因为中间的数为n,所以最小的奇数是n-2,最大的奇数是n+2,那么它们的积为n(n-2)(n+2)=n3-4n.
10.答案 -56
解析 因为2x3y5·(-4x4y2)=-8x7y7=mx7yn,
所以m=-8,n=7,
所以mn=-8×7=-56.
11.答案 (2n+1)2-1=2n(2n+2)(n为大于或等于1的整数)
解析 ①9-1=32-1=(2×1+1)2-1=2×(2+2)=2×4;
②25-1=52-1=(2×2+1)2-1=(2×2)×(2+2×2)=4×6;
③49-1=72-1=(2×3+1)2-1=(2×3)×(2+2×3)=6×8;
……
因此第n个等式为(2n+1)2-1=2n(2n+2)(n为大于或等于1的整数).
12.答案 1
解析 ∵a-b=1,
∴原式=(a+b)(a-b)-2b=1×(a+b)-2b=a+b-2b=a-b=1.
13.答案 a+b=0
解析 (x-a)(x-b)=x2-(a+b)x+ab,
因为乘积中不含x的一次项,
所以a+b=0.
14.答案 x2-1
解析 根据题意得(x-1)※x=(x-1)(x+1)=x2-1.
15.答案 0
解析 根据题意得x3+ax2+bx+3=(x+1)(x2-2x+3),
即x3+ax2+bx+3=x3-x2+x+3,
所以a=-1,b=1,
所以a+b=-1+1=0.
16.答案 2b
解析 ∵S1=(AB-a)·a+(CD-b)(AD-a)
=(AB-a)·a+(AB-b)(AD-a),
S2=AB(AD-a)+(a-b)(AB-a),
∴S2-S1=AB(AD-a)+(a-b)(AB-a)-(AB-a)·a-(AB-b)(AD-a)
=(AD-a)(AB-AB+b)+(AB-a)(a-b-a)
=b·AD-ab-b·AB+ab
=b(AD-AB).
∵AD-AB=2,
∴S2-S1=2b.
17.解析 (1)x3-9x=x(x2-9)=x(x+3)(x-3).
(2)16x4-8x2+1=(4x2-1)2=[(2x+1)(2x-1)]2
=(2x+1)2(2x-1)2.
18.解析 (1)原式=x2-4y2-(3y-4y2)
=x2-4y2-3y+4y2
=x2-3y.
(2)原式=x2+2x+x2+2x+1-4x=2x2+1.
19.解析 (1)平方差公式;完全平方公式.
(2)(a+2x-y-b)(a-2x+y-b)
=[(a-b)+(2x-y)][(a-b)-(2x-y)]
=(a-b)2-(2x-y)2
=a2-2ab+b2-4x2+4xy-y2.
20.解析 (a-3b)(a+3b)+(a-3b)2
=a2-(3b)2+(a2-6ab+9b2)
=a2-9b2+a2-6ab+9b2
=2a2-6ab,
当a=-3,b=时,原式=2×(-3)2-6×(-3)×=24.
21.解析 (1)设8-x=a,x-2=b,则(8-x)(x-2)=ab=5,a+b=(8-x)+(x-2)=6,
∴(8-x)2+(x-2)2=a2+b2=(a+b)2-2ab=36-10=26.
(2)∵AE=1,CF=3,AD=CD=x,
∴DE=x-1,DF=x-3.
∵长方形EMFD的面积是35,
∴DE·DF=(x-1)(x-3)=35.
设x-1=a,x-3=b,则ab=35,
a-b=(x-1)-(x-3)=2,
∴(a+b)2=(a-b)2+4ab=4+140=144.
又∵a+b>0,
∴a+b=12,
∴长方形EMFD的周长=2DE+2DF=2(a+b)=24.
22.解析 (1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac.
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2-2(ab+bc+ac)=121-76=45.
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2-(a+b)·b-a2
=a2+b2-ab
=(a+b)2-ab
=×102-×20
=50-30
=20.
(4)(i)(答案不唯一)根据题意,作出图形如下:
(ii)(a+2b)(2a+b).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024苏科版数学七年级下册
第9章 素养综合检测
(满分100分,限时60分钟)
一、选择题(本大题共8小题,每小题3分,共24分)
1.式子n2-1与n2+n的公因式是( )
A.n+1 B.n2 C.n D.n-1
2.(2023湖南长沙中考)下列计算正确的是( )
A.x2·x3=x5 B.(x3)3=x6 C.x(x+1)=x2+1 D.(2a-1)2=4a2-1
3.(2023江苏南京玄武期中)下列从左到右的变形是因式分解的是( )
A.ab+ac+d=a(b+c)+d
B.(a+1)(a-1)=a2-1
C.x2-2x+1=(x-1)2
D.a(a+1)=a2+a
4.若多项式x2+mx+4能用完全平方公式分解因式,则m的值是( )
A.2 B.-2 C.±4 D.±8
5.【新考向·代数推理】(2023河北中考)若k为任意整数,则(2k+3)2-4k2的值总能( )
A.被2整除 B.被3整除 C.被5整除 D.被7整除
6.我们所学的多项式因式分解的方法主要有①提公因式法;②平方差公式法;③完全平方公式法.现将多项式(x-y)3+4(y-x)进行因式分解,使用的方法有( )
A.①② B.①③ C.②③ D.①②③
7.【数形结合思想】如图,现有正方形A类、B类卡片和长方形C类卡片若干张,如果要拼成一个长为(a+3b),宽为(a+2b)的大长方形,则需要C类卡片( )
A.3张 B.4张
C.5张 D.6张
8.【新考向·新定义试题】在数学中,为了书写简便,数学家欧拉引进了求和符号“”.如:记k=1+2+3+…+(n-1)+n,(x+k)=(x+3)+(x+4)+…
+(x+n),已知[(x+k)(x-k+1)]=4x2+4x+m,则m的值是( )
A.40 B.-70 C.-40 D.-20
二、填空题(本大题共8小题,每小题3分,共24分)
9.三个连续奇数,中间的数是n,则它们的积是 .
10.如果单项式2x3y5与-4x4y2的积为mx7yn ,那么mn= .
11.观察等式:①9-1=2×4;②25-1=4×6;③49-1=6×8;……按照这种规律写出第n个等式: .
12.(2023江苏南京玄武期中)已知a-b=1,则a2-b2-2b的值为 .
13.如果x-a与x-b的乘积中不含x的一次项,那么a与b的关系为 .
14.【新考向·新定义试题】(2020浙江衢州中考)定义a※b=a(b+1),例如:2※3=2×(3+1)=2×4=8,则(x-1)※x的结果为 .
15.若关于x的三次四项式x3+ax2+bx+3能分解成(x+1)(x2-2x+3),则a+b= .
16.在长方形ABCD内,将如图①所示的两张边长分别为a和b(a>b)的正方形纸片按如图②③所示的两种方式放置(图②③中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图②中阴影部分的面积为S1,图③中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为 .
图① 图② 图③
三、解答题(本大题共6小题,共52分)
17.(2023江苏镇江期中)(10分)因式分解:
(1)x3-9x;
(2)16x4-8x2+1.
18.(10分)计算:
(1)(2023甘肃兰州中考)(x+2y)(x-2y)-y(3-4y);
(2)(2023山西中考)x(x+2)+(x+1)2-4x.
19.【新考向·过程性学习试题】(6分)阅读例题的解答过程,并解答(1)(2)中的问题.
例:计算(a-2b+3)(a+2b-3).
原式=[a-(2b-3)][a+(2b-3)]①
=a2-(2b-3)2②
=a2-(4b2-12b+9)③
=a2-4b2+12b-9.
(1)例题求解过程中,利用了整体思想,其中①→②的运算依据是 ,②→③的运算依据是 ;(填整式乘法公式的名称)
(2)用此方法计算:(a+2x-y-b)(a-2x+y-b).
20.(8分)先化简,再求值:(a-3b)(a+3b)+(a-3b)2,其中a=-3,b=.
21.(8分)若x满足(5-x)(x-2)=2,求(x-5)2+(2-x)2的值.
解:设5-x=a,x-2=b,则(5-x)(x-2)=ab=2,a+b=(5-x)+(x-2)=3,
∴(x-5)2+(2-x)2=(5-x)2+(x-2)2=a2+b2=(a+b)2-2ab=32-2×2=5.
请运用上面的方法求解下面的问题:
(1)若x满足(8-x)(x-2)=5,求(8-x)2+(x-2)2的值;
(2)如图,已知正方形ABCD的边长为x,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是35,求长方形EMFD的周长.
22.(10分)把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图①,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图②,可得等式: .
(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图③,将边长分别为a、b的两个正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若这两个正方形的边长a、b满足a+b=10,ab=20,请求出阴影部分的面积.
(4)图④中给出了边长分别为a、b的小正方形纸片和邻边长分别为a、b的长方形纸片,现有足量的这三种纸片.
(i)请用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,并仿照图①②画出拼法并标注a、b;
(ii)研究(i)中的拼图发现,可以分解因式2a2+5ab+2b2= .
答案全解全析
1.A ∵n2-1=(n+1)(n-1),n2+n=n(n+1),∴n2-1与n2+n的公因式是n+1.故选A.
2.A A.x2·x3=x5,本选项符合题意;
B.(x3)3=x9≠x6,本选项不符合题意;
C.x(x+1)=x2+x,本选项不符合题意;
D.(2a-1)2=4a2-4a+1≠4a2-1,本选项不符合题意.故选A.
3.C A.ab+ac+d=a(b+c)+d,右边不是几个整式的积的形式,不属于因式分解,故此选项不符合题意;
B.(a+1)(a-1)=a2-1,是整式的乘法,不属于因式分解,故此选项不符合题意;
C.x2-2x+1=(x-1)2,右边是几个整式的积的形式,属于因式分解,故此选项符合题意;
D.a(a+1)=a2+a,是整式的乘法,不属于因式分解,故此选项不符合题意.
故选C.
4.C 当m=4时,x2+4x+4=(x+2)2,当m=-4时,x2-4x+4=(x-2)2,所以m=±4.故选C.
5.B (2k+3)2-4k2=4k2+12k+9-4k2=12k+9=3(4k+3),
∵k为任意整数,
∴(2k+3)2-4k2的值总能被3整除,故选B.
6.A (x-y)3+4(y-x)=(x-y)3-4(x-y)=(x-y)[(x-y)2-4]=(x-y)(x-y+2)(x-y-2),故将多项式(x-y)3+4(y-x)进行因式分解,使用的方法有①提公因式法,②平方差公式法.故选A.
7.C 因为(a+3b)(a+2b)=a2+2ab+3ab+6b2=a2+5ab+6b2,所以需要A类卡片1张、B类卡片6张、C类卡片5张.故选C.
8.C ∵x2项的系数是4,∴n=5,
∴(x+2)(x-1)+(x+3)(x-2)+(x+4)(x-3)+(x+5)(x-4)=(x2+x-2)+(x2+x-6)+(x2+x-12)+(x2+x-20)=4x2+4x-40.
∵[(x+k)(x-k+1)]=4x2+4x+m,∴m=-40.故选C.
9.答案 n3-4n
解析 因为中间的数为n,所以最小的奇数是n-2,最大的奇数是n+2,那么它们的积为n(n-2)(n+2)=n3-4n.
10.答案 -56
解析 因为2x3y5·(-4x4y2)=-8x7y7=mx7yn,
所以m=-8,n=7,
所以mn=-8×7=-56.
11.答案 (2n+1)2-1=2n(2n+2)(n为大于或等于1的整数)
解析 ①9-1=32-1=(2×1+1)2-1=2×(2+2)=2×4;
②25-1=52-1=(2×2+1)2-1=(2×2)×(2+2×2)=4×6;
③49-1=72-1=(2×3+1)2-1=(2×3)×(2+2×3)=6×8;
……
因此第n个等式为(2n+1)2-1=2n(2n+2)(n为大于或等于1的整数).
12.答案 1
解析 ∵a-b=1,
∴原式=(a+b)(a-b)-2b=1×(a+b)-2b=a+b-2b=a-b=1.
13.答案 a+b=0
解析 (x-a)(x-b)=x2-(a+b)x+ab,
因为乘积中不含x的一次项,
所以a+b=0.
14.答案 x2-1
解析 根据题意得(x-1)※x=(x-1)(x+1)=x2-1.
15.答案 0
解析 根据题意得x3+ax2+bx+3=(x+1)(x2-2x+3),
即x3+ax2+bx+3=x3-x2+x+3,
所以a=-1,b=1,
所以a+b=-1+1=0.
16.答案 2b
解析 ∵S1=(AB-a)·a+(CD-b)(AD-a)
=(AB-a)·a+(AB-b)(AD-a),
S2=AB(AD-a)+(a-b)(AB-a),
∴S2-S1=AB(AD-a)+(a-b)(AB-a)-(AB-a)·a-(AB-b)(AD-a)
=(AD-a)(AB-AB+b)+(AB-a)(a-b-a)
=b·AD-ab-b·AB+ab
=b(AD-AB).
∵AD-AB=2,
∴S2-S1=2b.
17.解析 (1)x3-9x=x(x2-9)=x(x+3)(x-3).
(2)16x4-8x2+1=(4x2-1)2=[(2x+1)(2x-1)]2
=(2x+1)2(2x-1)2.
18.解析 (1)原式=x2-4y2-(3y-4y2)
=x2-4y2-3y+4y2
=x2-3y.
(2)原式=x2+2x+x2+2x+1-4x=2x2+1.
19.解析 (1)平方差公式;完全平方公式.
(2)(a+2x-y-b)(a-2x+y-b)
=[(a-b)+(2x-y)][(a-b)-(2x-y)]
=(a-b)2-(2x-y)2
=a2-2ab+b2-4x2+4xy-y2.
20.解析 (a-3b)(a+3b)+(a-3b)2
=a2-(3b)2+(a2-6ab+9b2)
=a2-9b2+a2-6ab+9b2
=2a2-6ab,
当a=-3,b=时,原式=2×(-3)2-6×(-3)×=24.
21.解析 (1)设8-x=a,x-2=b,则(8-x)(x-2)=ab=5,a+b=(8-x)+(x-2)=6,
∴(8-x)2+(x-2)2=a2+b2=(a+b)2-2ab=36-10=26.
(2)∵AE=1,CF=3,AD=CD=x,
∴DE=x-1,DF=x-3.
∵长方形EMFD的面积是35,
∴DE·DF=(x-1)(x-3)=35.
设x-1=a,x-3=b,则ab=35,
a-b=(x-1)-(x-3)=2,
∴(a+b)2=(a-b)2+4ab=4+140=144.
又∵a+b>0,
∴a+b=12,
∴长方形EMFD的周长=2DE+2DF=2(a+b)=24.
22.解析 (1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac.
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2-2(ab+bc+ac)=121-76=45.
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2-(a+b)·b-a2
=a2+b2-ab
=(a+b)2-ab
=×102-×20
=50-30
=20.
(4)(i)(答案不唯一)根据题意,作出图形如下:
(ii)(a+2b)(2a+b).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
