江苏省省熟中2023-2024学年高一上学期12月学业水平调研数学试卷(PDF版含答案)
文档属性
| 名称 | 江苏省省熟中2023-2024学年高一上学期12月学业水平调研数学试卷(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 763.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 21:53:32 | ||
图片预览




文档简介
2023~2024 年度第一学期高一年级十二月份学业水平调研
数学试题(1-12 班)
一、单项选择题(本大题共 8 小题,每小题 5 分,共计 40 分.在每小题给出的四个选项中,只有一个是
符合要求的.)
1、已知集合 , ,则 ( )
A. B. C. D.
2、函数 f x lnx x 4的零点一定位于下列哪个区间( )
A. 1,2 B. 2,3 C. 3,4 D. 5,6
3、“ 为第一或第四象限角”是“ cos 0 ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4、如图是杭州 2022 年第 19 届亚运会会徽,名为“潮
涌”,形象象征着新时代中国特色社会主义大潮的涌动和
发展.如图是会徽的几何图形,设弧 AD 的长度是 l1,弧 BC
的长度是 l2,几何图形 ABCD 面积为 S1,扇形 BOC 面积为
l1 S
S2,若 4
1
, ( )
l2 S
2
A.9 B.8 C.16 D.15
5、角
3
的终边与单位圆 O相交于点 P,且点 P的横坐标为 ,则
5 1 sin
2 的值为( )
3 3 4 4
A. B.- C. D.
5 5 5 5
6、已知 , , ,则 , , 的大小关系是( ).
A. B. C. D.
7、已知函数 ,且 ,则实数 的取值范围是( )
A. B. C. D.
8、函数 f x loga 2x 3 1( a 0 且a 1)的图象恒过定点 A m,n ,若对任意正数 都有
1 2
,则 的最小值是(
)
x 1 y
39 4
A.2 B. C.1 D.
22 3
二、选择题(本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题目要求.全
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
部选对的得 5 分,部分选对的得 2分,不选或有选错的得 0分.)
9、若角 A,B,C是 ABC 的三个内角,则下列等式中一定成立的是( )
A.cos(A B) cosC B.sin(A B) sinC
A C B B C A
C.cos sin D.sin cos
2 2 2 2
10、已知 π,0 7, sin cos ,则下列结论正确的是( )
13
π 12 5 17A. π, B.cos C. tan D.sin cos
2 13 12 13
|x|
1
11、已知函数 f (x) a b的图象过原点,且无限接近直线 y 3 ,但又不与该直线相交,则( )
4
A.a 3,b 3 B. f ( x ) 的值域为 (0,3)
C.若 f (x) f (y),且 x y,则 x y 0 D.若 x y 0,则 f (x) f (y)
log2 x , x 012、已知函数 f x 函数 g(x) [ f (x)]2x (m 3) f (x) 3m,则( )
2 , x 0
A.函数 f ( x ) 的值域为 (0, )
B.存在实数m,使得 f (m ) f ( m )
C.若 g(x) 1恒成立,则实数m的取值范围为
D.若函数 g(x)恰好有 5个零点,则函数 g(x)的 5个零点之积的取值范围是 ( ,0]
三、填空题(本题共 4 小题,每小题 5分,共 20 分.请把答案填写在答题卷划线位置上.)
2
13、函数 f (x) (m2 m 1)xm m 3是幂函数,且当 x (0, )时, f ( x ) 是减函数,则实数m= .
2x a 2 x 1
14、已知函数 f (x) (a R)为偶函数,则 f (1) f ( )
x 2
15、写出一个同时满足下列条件的非常数函数 .
①在[0, )单调递减 ②值域 (0,1] ③
16、校园内因改造施工,工人师傅用三角支架固定墙面(墙面与地面垂
直)(如图),现在一支架斜杆长为16dm,一端靠在墙上,另一端落在地
面上,则该支架斜杆与其在墙面和地面上射影所围成三角形周长的最大
值为 dm;现为调整支架安全性,要求前述直角三角形周长
为30dm,面积为30dm2,则此时斜杆长度应设计为 dm .
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
四、解答题(本题共 6 小题,共 70 分.请在答题卷指定区域内作答,解答时应写出文字说明,证明过程
或演算步骤.)
3 7
cos sin 2 2 17、已知
f ( )
sin( )
(1)化简 f ( );
1(2)若 f ( ) ,求 tan 的值;
3
1 5 (3)若 f
6
,求 f
3
6
的值.
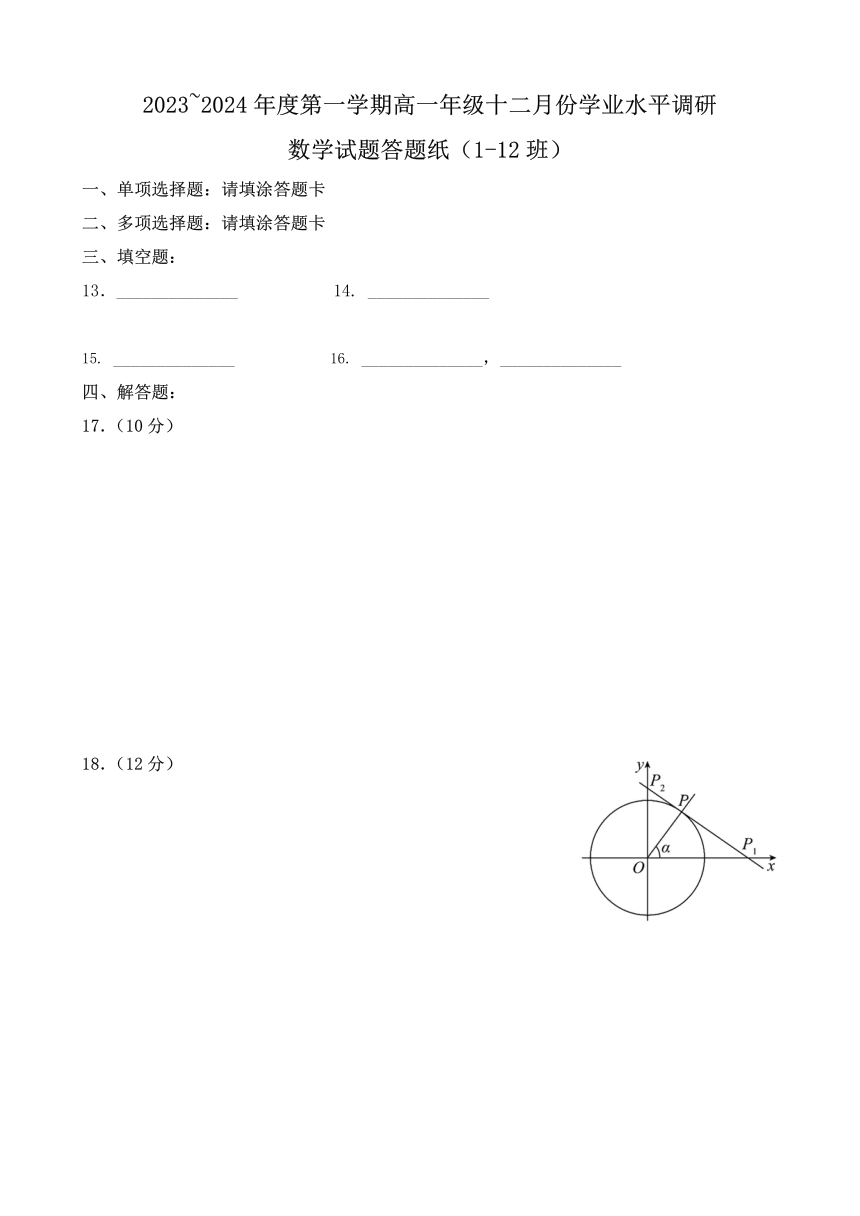
18、如图,在平面直角坐标系中,锐角 的始边与 x轴的非负半轴重合,终边与单位圆(圆心在原点,半
径为 1)交于点 P .过点 P作圆O的切线,分别交 x轴、 y轴于点P1 x0 ,0 与P2 0, y0 .
(1)若 ,求 P的坐标
6
(2)若 OP1P2的面积为 2,求 tan 的值;
2
(3)求 x0 9y
2
0 的最小值.
A x log 2x 4 log x 9 B x | x2 219、设集合 1 1 , 3mx 2m m 1 0 .
2 2
(1)若 B为空集,求实数m的取值范围;
(2)若B A,求实数m的取值范围.
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
20、已知函数 .
(1)当 x 2,8 时,求该函数的值域;
(2)若不等式 f x mlog2x在 x 4,16 上有解,求m的取值范围.
2 x a
21、设 f (x) (a为实常数), y g(x)与 y e x的图像关于原点对称.
1 x
g (x)
(1)当a 0,若关于 的方程 f [g (x)] 有两个不等实根,求m的范围;
m
(2)当 a 1,求方程 f (x) g(x)的实数根的个数,并加以证明.
1
22、已知 f x ex 2x . e
(1)求函数 f x 在 0, 的最小值.
x
(2)对于任意 x1, x2 0, ,都有 f x1 ln 3 a e 2 1 ln3a 2x2成立,求a的取值范围.
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
2023~2024 年度第一学期高一年级十二月份学业水平调研
数学试题答题纸(1-12 班)
一、单项选择题:请填涂答题卡
二、多项选择题:请填涂答题卡
三、填空题:
13.______________ 14. ______________
15. ______________ 16. ______________,______________
四、解答题:
17.(10 分)
18.(12 分)
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
19.(12 分)
20.(12 分)
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
21.(12 分)
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
22.(12 分)
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
2023~2024 年度第一学期高一年级十二月份学业水平调研
数学试题答案(1-12 班)
一、单项选题:
1.C 2.B 3.A 4.D 5.A 6.B 7.B 8.D
二、多项选择题:
9.AB 10.BD 11.AC 12.BCD
三、填空题:
13. -1 14. 15. (答案不唯一) 16. ,13.
四、解答题:
( sin ) ( cos )17. 解:(1) f ( ) cos
sin
(2) f (
1
) cos ,
3
2 2 2 sin 当 为第一象限角时,sin 1 cos , tan 2 2
3 cos
2 2 2
sin
当 为第四象限角时,sin 1 cos , tan 2 2
3 cos
1
(3)因为 f cos ,
6 6 3
5 5
所以 f cos
cos
6 6
6
1 cos
6
3
π π 3 1
18、(1)由题意得P cos ,sin ,所以P cos , sin ,即P , . 6 6 2 2
(2)由题意得 为锐角,故 P在第一象限,则P1,P2 在 x, y轴正半轴上,
1 1
由题意可知OP PP ,故cos 1 2 x OP ,故 0 , 1 cos
OP P ,故sin
1
1
2 OP ,则
y0 ,
2 sin
由 1
1 1 1 1
OP1P2的面积为 2,得 x y 2,即 2 .所以 sin cos ,
2 0 0 2 cos sin 4
2 2 sin cos 1 tan 1又 sin cos 1,故 2 2 ,即 , sin cos 4 tan2 1 4
所以 tan2 4tan 1 0,解得 tan 2 3 ;
(3)由题意 是锐角,则 x0 0, y0 0,
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
1 9 1 9
x20 9y
2
0
sin2 cos2
cos2
sin2 cos2 sin2
sin2 9cos2 sin2 9cos2
10 10 2 16,
cos2 sin2 cos2 sin2
sin2 9cos2 3
当且仅当 ,即sin , 时取等号,
cos2 sin2 2 3
2 2
所以 x0 9y0 的最小值为 16.
19.(1)依题意,不等式 x2 3mx 2m2 m 1 0解集为空集,
于是 9m2 4(2m2 m 1) 0,即m2 4m 4 0,解得m 2,
所以m 2 .
1
(2)不等式 log 1 (2x 4) log (x 9) 0 2x 4 x 9,解得 2 x 5,即 A x 2 x 5 ,
2 2
x2 3mx 2m2 m 1 0 [x (2m 1)][x (m 1)] 0,
当m 2时,B A,则m 2;
当m 2时,2m 1 m 1,则B (2m 1,m 1),而m 1 3 2,显然 B不是A的子集;
当m 2时,2m 1 m 1,则B (m 1,2m 1),
由B A,得 2 m 1 2m 1 5,解得 1 m 2,
所以m的取值范围是m 2或 1 m 2 .
20. (1)由对数函数单调性可知,当 x 2,8 时, log2x 1,3 ,
令 log2x t, t 1,3 ,即可得 f t t2 3t 2, t 1,3 ,
3 1
由二次函数性质可知当 t 时, f t ,当 t 3min 时, f t 22 4 max ;
因此可得当 x 2,8 1 时,该函数的值域为 , 2 4 .
(2)当 x 4,16 时,可得 log2x 2,4 ,
原不等式可化为 t2 3t 2 mt 在 t 2,4 上有解,
2 2
即可得 t 3 m在 t 2,4 上有解,易知函数 y t 3 在 t 2,4 上单调递增,
t t
所以 ,得 ;
即m的取值范围是 .
21. (1)设点P(x, y)为 g(x)图象上任意一点,P(x, y)关于原点的对称点为P ' ( x, y),
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
由题意可知P ' ( x, y)在 y e x上,则有, y ex,故 g(x) ex
2 x
a 0时, f (x)
1 x
g(x) x x
由 f [g(x)]
2 e e
可得, ,即e2x (1 m)ex 2m 0
m 1 ex m
令 ex t,则 t2 (1 m)t 2m 0有两个不等正根
21 m 4( 2m) 0
则有, (1 m) 0 ,解之得,m 5 2 6
2m 0
2 x a 3 a
(2)令h(x) g(x) f (x) ex ex 1
1 x x 1
由 a 1,可知a 3 0,
3 a
则 x 1时, y ex 1与 y 均单调递增,故h(x)在( 1, )上单调递增,
x 1
又 a 1时,h(0) e0 1 (a 3) 1 a 0,
a 3 a 1
h(1) e1 1 e e 1 0
2 2
故 h(x)在 ( 1, )上有唯一零点;
又当 x (
3 a
, 1)时,h(x) ex 1 0恒成立,即h(x)在 ( , 1)上无零点.
x 1
综上可知,方程 f (x) g(x)有且仅有一个实数根.
1 1
22. (1)因为 f x ex 2 2 ex 2 0,
ex ex
x 1
当且仅当e x ,即 x 0时,等号成立. e
所以,函数 f x 在 0, 的最小值为 0.
x
(2)设 g x2 ln 3 a e 2 1 ln3a 2x2,
由(1)知,函数 f x 在 0, 的最小值为 0.
则由任意 x1, x2 0, ,都有 f x1 ln 3 a e
x2 1 ln3a 2x2成立,
可得 ln 3 a e
x2 1 ln3a 2x2 0在 0, 上恒成立,
只需 g x2 0max 在 0, 上恒成立即可.
因为 3 a ex2 1 0,3a 0在 0, 上恒成立,
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
1
a 3
所以 ex2 .
a 0
1
因为 x2 0,所以ex2 1,3 3 4x , e 2
所以0 a 3.
ln 3 a ex由 2 1 ln3a 2x2 0可得,
ln x2 2x2 3 a e 1 ln3a 2x2 ln 3ae .
因为 y ln x单调递增,
所以 3 a ex2 1 3ae2x2 ,
即3ae
2x2 3 a ex2 1 0在 0, 上恒成立.
2x 2
因为3ae 2 3 a ex2 1 3a ex2 3 a ex2 1 aex2 1 3ex2 1 ,
所以, aex2 1 3ex2 1 0在 0, 上恒成立.
因为,3ex2 1 0在 0, 上恒成立,
所以,aex2 1 0在 0, 上恒成立,
1
所以,a 在 0, 上恒成立.
ex2
1
因为 y 在 0, x 上为减函数, e 2
1
所以 y x 在 x2 0处取得最大值 1, e 2
所以,a 1.
综上所述,1 a 3.
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
数学试题(1-12 班)
一、单项选择题(本大题共 8 小题,每小题 5 分,共计 40 分.在每小题给出的四个选项中,只有一个是
符合要求的.)
1、已知集合 , ,则 ( )
A. B. C. D.
2、函数 f x lnx x 4的零点一定位于下列哪个区间( )
A. 1,2 B. 2,3 C. 3,4 D. 5,6
3、“ 为第一或第四象限角”是“ cos 0 ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4、如图是杭州 2022 年第 19 届亚运会会徽,名为“潮
涌”,形象象征着新时代中国特色社会主义大潮的涌动和
发展.如图是会徽的几何图形,设弧 AD 的长度是 l1,弧 BC
的长度是 l2,几何图形 ABCD 面积为 S1,扇形 BOC 面积为
l1 S
S2,若 4
1
, ( )
l2 S
2
A.9 B.8 C.16 D.15
5、角
3
的终边与单位圆 O相交于点 P,且点 P的横坐标为 ,则
5 1 sin
2 的值为( )
3 3 4 4
A. B.- C. D.
5 5 5 5
6、已知 , , ,则 , , 的大小关系是( ).
A. B. C. D.
7、已知函数 ,且 ,则实数 的取值范围是( )
A. B. C. D.
8、函数 f x loga 2x 3 1( a 0 且a 1)的图象恒过定点 A m,n ,若对任意正数 都有
1 2
,则 的最小值是(
)
x 1 y
39 4
A.2 B. C.1 D.
22 3
二、选择题(本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题目要求.全
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
部选对的得 5 分,部分选对的得 2分,不选或有选错的得 0分.)
9、若角 A,B,C是 ABC 的三个内角,则下列等式中一定成立的是( )
A.cos(A B) cosC B.sin(A B) sinC
A C B B C A
C.cos sin D.sin cos
2 2 2 2
10、已知 π,0 7, sin cos ,则下列结论正确的是( )
13
π 12 5 17A. π, B.cos C. tan D.sin cos
2 13 12 13
|x|
1
11、已知函数 f (x) a b的图象过原点,且无限接近直线 y 3 ,但又不与该直线相交,则( )
4
A.a 3,b 3 B. f ( x ) 的值域为 (0,3)
C.若 f (x) f (y),且 x y,则 x y 0 D.若 x y 0,则 f (x) f (y)
log2 x , x 012、已知函数 f x 函数 g(x) [ f (x)]2x (m 3) f (x) 3m,则( )
2 , x 0
A.函数 f ( x ) 的值域为 (0, )
B.存在实数m,使得 f (m ) f ( m )
C.若 g(x) 1恒成立,则实数m的取值范围为
D.若函数 g(x)恰好有 5个零点,则函数 g(x)的 5个零点之积的取值范围是 ( ,0]
三、填空题(本题共 4 小题,每小题 5分,共 20 分.请把答案填写在答题卷划线位置上.)
2
13、函数 f (x) (m2 m 1)xm m 3是幂函数,且当 x (0, )时, f ( x ) 是减函数,则实数m= .
2x a 2 x 1
14、已知函数 f (x) (a R)为偶函数,则 f (1) f ( )
x 2
15、写出一个同时满足下列条件的非常数函数 .
①在[0, )单调递减 ②值域 (0,1] ③
16、校园内因改造施工,工人师傅用三角支架固定墙面(墙面与地面垂
直)(如图),现在一支架斜杆长为16dm,一端靠在墙上,另一端落在地
面上,则该支架斜杆与其在墙面和地面上射影所围成三角形周长的最大
值为 dm;现为调整支架安全性,要求前述直角三角形周长
为30dm,面积为30dm2,则此时斜杆长度应设计为 dm .
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
四、解答题(本题共 6 小题,共 70 分.请在答题卷指定区域内作答,解答时应写出文字说明,证明过程
或演算步骤.)
3 7
cos sin 2 2 17、已知
f ( )
sin( )
(1)化简 f ( );
1(2)若 f ( ) ,求 tan 的值;
3
1 5 (3)若 f
6
,求 f
3
6
的值.
18、如图,在平面直角坐标系中,锐角 的始边与 x轴的非负半轴重合,终边与单位圆(圆心在原点,半
径为 1)交于点 P .过点 P作圆O的切线,分别交 x轴、 y轴于点P1 x0 ,0 与P2 0, y0 .
(1)若 ,求 P的坐标
6
(2)若 OP1P2的面积为 2,求 tan 的值;
2
(3)求 x0 9y
2
0 的最小值.
A x log 2x 4 log x 9 B x | x2 219、设集合 1 1 , 3mx 2m m 1 0 .
2 2
(1)若 B为空集,求实数m的取值范围;
(2)若B A,求实数m的取值范围.
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
20、已知函数 .
(1)当 x 2,8 时,求该函数的值域;
(2)若不等式 f x mlog2x在 x 4,16 上有解,求m的取值范围.
2 x a
21、设 f (x) (a为实常数), y g(x)与 y e x的图像关于原点对称.
1 x
g (x)
(1)当a 0,若关于 的方程 f [g (x)] 有两个不等实根,求m的范围;
m
(2)当 a 1,求方程 f (x) g(x)的实数根的个数,并加以证明.
1
22、已知 f x ex 2x . e
(1)求函数 f x 在 0, 的最小值.
x
(2)对于任意 x1, x2 0, ,都有 f x1 ln 3 a e 2 1 ln3a 2x2成立,求a的取值范围.
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
2023~2024 年度第一学期高一年级十二月份学业水平调研
数学试题答题纸(1-12 班)
一、单项选择题:请填涂答题卡
二、多项选择题:请填涂答题卡
三、填空题:
13.______________ 14. ______________
15. ______________ 16. ______________,______________
四、解答题:
17.(10 分)
18.(12 分)
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
19.(12 分)
20.(12 分)
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
21.(12 分)
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
22.(12 分)
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
2023~2024 年度第一学期高一年级十二月份学业水平调研
数学试题答案(1-12 班)
一、单项选题:
1.C 2.B 3.A 4.D 5.A 6.B 7.B 8.D
二、多项选择题:
9.AB 10.BD 11.AC 12.BCD
三、填空题:
13. -1 14. 15. (答案不唯一) 16. ,13.
四、解答题:
( sin ) ( cos )17. 解:(1) f ( ) cos
sin
(2) f (
1
) cos ,
3
2 2 2 sin 当 为第一象限角时,sin 1 cos , tan 2 2
3 cos
2 2 2
sin
当 为第四象限角时,sin 1 cos , tan 2 2
3 cos
1
(3)因为 f cos ,
6 6 3
5 5
所以 f cos
cos
6 6
6
1 cos
6
3
π π 3 1
18、(1)由题意得P cos ,sin ,所以P cos , sin ,即P , . 6 6 2 2
(2)由题意得 为锐角,故 P在第一象限,则P1,P2 在 x, y轴正半轴上,
1 1
由题意可知OP PP ,故cos 1 2 x OP ,故 0 , 1 cos
OP P ,故sin
1
1
2 OP ,则
y0 ,
2 sin
由 1
1 1 1 1
OP1P2的面积为 2,得 x y 2,即 2 .所以 sin cos ,
2 0 0 2 cos sin 4
2 2 sin cos 1 tan 1又 sin cos 1,故 2 2 ,即 , sin cos 4 tan2 1 4
所以 tan2 4tan 1 0,解得 tan 2 3 ;
(3)由题意 是锐角,则 x0 0, y0 0,
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
1 9 1 9
x20 9y
2
0
sin2 cos2
cos2
sin2 cos2 sin2
sin2 9cos2 sin2 9cos2
10 10 2 16,
cos2 sin2 cos2 sin2
sin2 9cos2 3
当且仅当 ,即sin , 时取等号,
cos2 sin2 2 3
2 2
所以 x0 9y0 的最小值为 16.
19.(1)依题意,不等式 x2 3mx 2m2 m 1 0解集为空集,
于是 9m2 4(2m2 m 1) 0,即m2 4m 4 0,解得m 2,
所以m 2 .
1
(2)不等式 log 1 (2x 4) log (x 9) 0 2x 4 x 9,解得 2 x 5,即 A x 2 x 5 ,
2 2
x2 3mx 2m2 m 1 0 [x (2m 1)][x (m 1)] 0,
当m 2时,B A,则m 2;
当m 2时,2m 1 m 1,则B (2m 1,m 1),而m 1 3 2,显然 B不是A的子集;
当m 2时,2m 1 m 1,则B (m 1,2m 1),
由B A,得 2 m 1 2m 1 5,解得 1 m 2,
所以m的取值范围是m 2或 1 m 2 .
20. (1)由对数函数单调性可知,当 x 2,8 时, log2x 1,3 ,
令 log2x t, t 1,3 ,即可得 f t t2 3t 2, t 1,3 ,
3 1
由二次函数性质可知当 t 时, f t ,当 t 3min 时, f t 22 4 max ;
因此可得当 x 2,8 1 时,该函数的值域为 , 2 4 .
(2)当 x 4,16 时,可得 log2x 2,4 ,
原不等式可化为 t2 3t 2 mt 在 t 2,4 上有解,
2 2
即可得 t 3 m在 t 2,4 上有解,易知函数 y t 3 在 t 2,4 上单调递增,
t t
所以 ,得 ;
即m的取值范围是 .
21. (1)设点P(x, y)为 g(x)图象上任意一点,P(x, y)关于原点的对称点为P ' ( x, y),
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
由题意可知P ' ( x, y)在 y e x上,则有, y ex,故 g(x) ex
2 x
a 0时, f (x)
1 x
g(x) x x
由 f [g(x)]
2 e e
可得, ,即e2x (1 m)ex 2m 0
m 1 ex m
令 ex t,则 t2 (1 m)t 2m 0有两个不等正根
21 m 4( 2m) 0
则有, (1 m) 0 ,解之得,m 5 2 6
2m 0
2 x a 3 a
(2)令h(x) g(x) f (x) ex ex 1
1 x x 1
由 a 1,可知a 3 0,
3 a
则 x 1时, y ex 1与 y 均单调递增,故h(x)在( 1, )上单调递增,
x 1
又 a 1时,h(0) e0 1 (a 3) 1 a 0,
a 3 a 1
h(1) e1 1 e e 1 0
2 2
故 h(x)在 ( 1, )上有唯一零点;
又当 x (
3 a
, 1)时,h(x) ex 1 0恒成立,即h(x)在 ( , 1)上无零点.
x 1
综上可知,方程 f (x) g(x)有且仅有一个实数根.
1 1
22. (1)因为 f x ex 2 2 ex 2 0,
ex ex
x 1
当且仅当e x ,即 x 0时,等号成立. e
所以,函数 f x 在 0, 的最小值为 0.
x
(2)设 g x2 ln 3 a e 2 1 ln3a 2x2,
由(1)知,函数 f x 在 0, 的最小值为 0.
则由任意 x1, x2 0, ,都有 f x1 ln 3 a e
x2 1 ln3a 2x2成立,
可得 ln 3 a e
x2 1 ln3a 2x2 0在 0, 上恒成立,
只需 g x2 0max 在 0, 上恒成立即可.
因为 3 a ex2 1 0,3a 0在 0, 上恒成立,
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
1
a 3
所以 ex2 .
a 0
1
因为 x2 0,所以ex2 1,3 3 4x , e 2
所以0 a 3.
ln 3 a ex由 2 1 ln3a 2x2 0可得,
ln x2 2x2 3 a e 1 ln3a 2x2 ln 3ae .
因为 y ln x单调递增,
所以 3 a ex2 1 3ae2x2 ,
即3ae
2x2 3 a ex2 1 0在 0, 上恒成立.
2x 2
因为3ae 2 3 a ex2 1 3a ex2 3 a ex2 1 aex2 1 3ex2 1 ,
所以, aex2 1 3ex2 1 0在 0, 上恒成立.
因为,3ex2 1 0在 0, 上恒成立,
所以,aex2 1 0在 0, 上恒成立,
1
所以,a 在 0, 上恒成立.
ex2
1
因为 y 在 0, x 上为减函数, e 2
1
所以 y x 在 x2 0处取得最大值 1, e 2
所以,a 1.
综上所述,1 a 3.
{#{QQABbQyQgggoAABAARhCQQ3ICEGQkAECCIoORFAEoAAAgAFABAA=}#}
同课章节目录
