三角形内角和课件
图片预览


文档简介
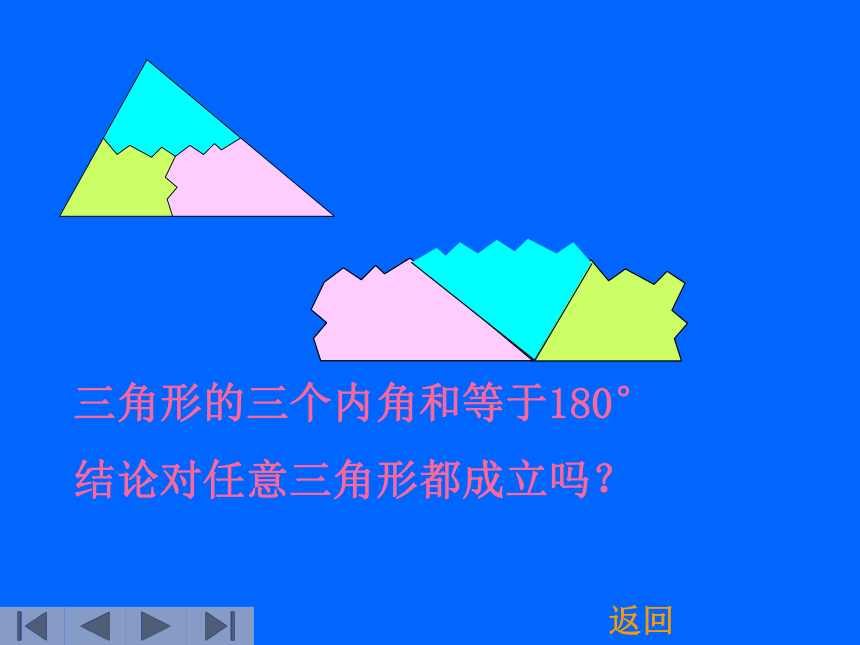
课件16张PPT。三角形的内角和想一想三角形的三个内角和是多少?把三个角拼在一起试试看有什么办法可以验证呢?返回三角形的三个内角和等于180°
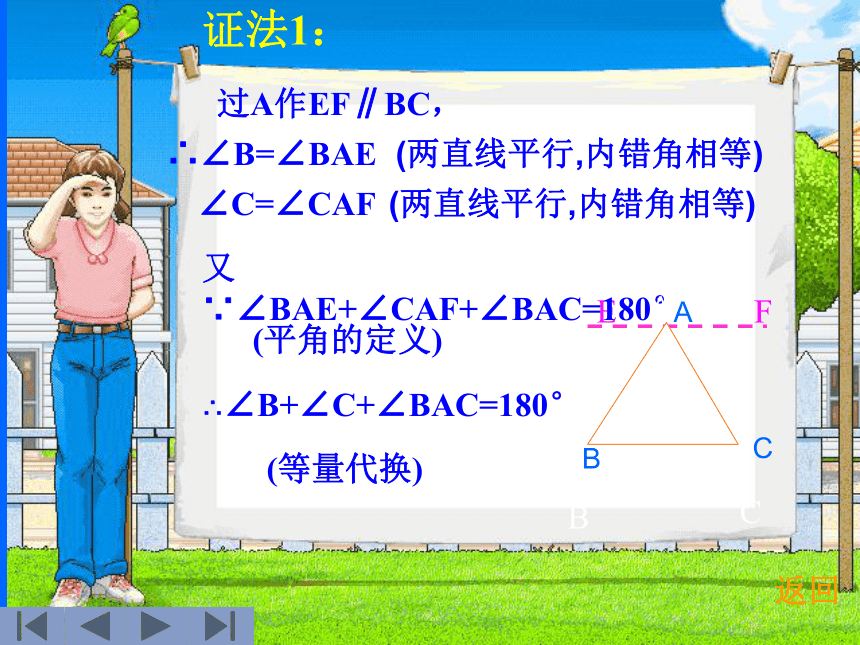
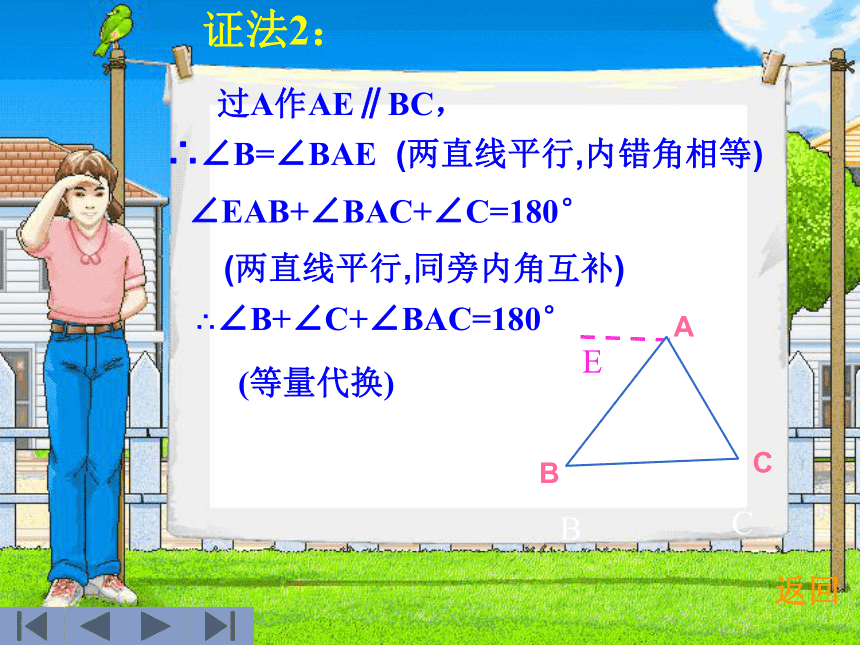
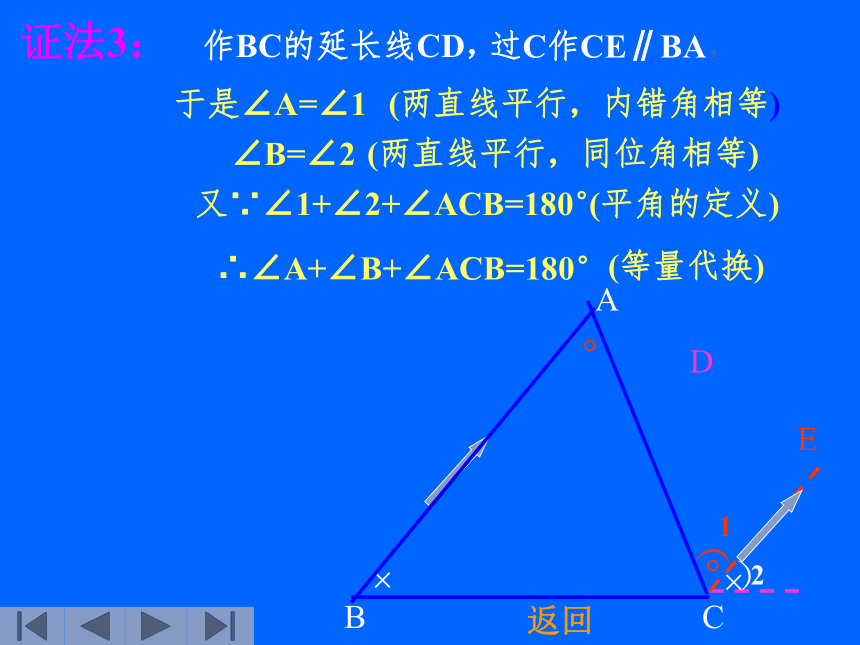
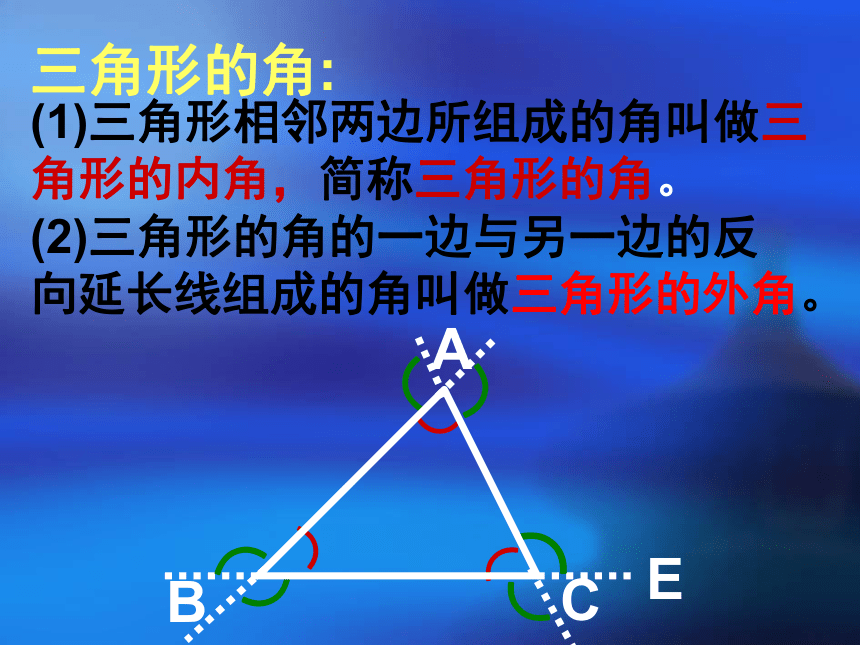
结论对任意三角形都成立吗? 返回证法1:ABC过A作EF∥BC,EF∴∠B=∠BAE(两直线平行,内错角相等) ∠C=∠CAF(两直线平行,内错角相等)又∵∠BAE+∠CAF+∠BAC=180°∴∠B+∠C+∠BAC=180°(平角的定义)(等量代换)返回ABCA证法2:ABC过A作AE∥BC,E∴∠B=∠BAE(两直线平行,内错角相等)∠EAB+∠BAC+∠C=180°(两直线平行,同旁内角互补)∴∠B+∠C+∠BAC=180°(等量代换)返回CABAD过C作CE∥BA,)E1。于是∠A=∠1(两直线平行,内错角相等)∠B=∠2又∵∠1+∠2+∠ACB=180°(平角的定义)∴∠A+∠B+∠ACB=180°(两直线平行,同位角相等))BC(等量代换)证法3:作BC的延长线CD,返回三角形的角:(1)三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。(2)三角形的角的一边与另一边的反向延长线组成的角叫做三角形的外角。))))))EA 如图,①图中有几个角是△ABC的外角?说出它们的名称。②∠1、 ∠2是不是△ABC的外角?为什么?练习三角形的外角性质(1)三角形的一个外角等于和它不相邻的两个内角的和。
(2)三角形的一个外角大于与它不相邻的任何一个内角。 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.三角形内角和定理:
三角形的内角和等于1800.返回检验一下自己吧!1、 在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。解:在△ABC中,
∠A+∠B+∠C=180°,
∠A=80°∴∠B+∠C=100°∵∠B=∠C ∴∠B=∠C=500 ABC2、已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。解:设三个内角度数分别为:x ° ,3x ° ,5x °,
由三角形内角和为180°得x+3x+5x=180解得 x=20所以三个内角度数分别为20°,60°,100°。3.已知:在△ABC中, ∠C=∠ABC=2∠A,BD 是AC边上的高。求∠DBC的度数。 解:设∠A=x°,则∠C=∠ABC=2X0∴x+2x+2x=180 解得:x=36在△BDC中, ∵∠BDC=90° ∴∠DBC=180°-∠BDC- ∠C =180°-90°-72° =18 °∴∠C=72°练习11△ABC中,若∠A+∠B=∠C,则△ABC是()
A、锐角△ B、直角△ C、钝角△ D、等腰△2 一个三角形至少有()
A、一个锐角 B、两个锐角 C、一个钝角 D、一个直角3 如图△ABC中,CD平分∠ACB,DE∥BC, ∠A=70∠B=50,求∠BDC的度数。动脑筋,你能行!练习21如图△ABC中,∠ABC、∠ACB的平分线交于点O, ⑴若∠A=70°,求∠BOC。 ⑵若∠A=X°,求∠BOC。动脑筋,你能行!这节课你有那些收获?
结论对任意三角形都成立吗? 返回证法1:ABC过A作EF∥BC,EF∴∠B=∠BAE(两直线平行,内错角相等) ∠C=∠CAF(两直线平行,内错角相等)又∵∠BAE+∠CAF+∠BAC=180°∴∠B+∠C+∠BAC=180°(平角的定义)(等量代换)返回ABCA证法2:ABC过A作AE∥BC,E∴∠B=∠BAE(两直线平行,内错角相等)∠EAB+∠BAC+∠C=180°(两直线平行,同旁内角互补)∴∠B+∠C+∠BAC=180°(等量代换)返回CABAD过C作CE∥BA,)E1。于是∠A=∠1(两直线平行,内错角相等)∠B=∠2又∵∠1+∠2+∠ACB=180°(平角的定义)∴∠A+∠B+∠ACB=180°(两直线平行,同位角相等))BC(等量代换)证法3:作BC的延长线CD,返回三角形的角:(1)三角形相邻两边所组成的角叫做三角形的内角,简称三角形的角。(2)三角形的角的一边与另一边的反向延长线组成的角叫做三角形的外角。))))))EA 如图,①图中有几个角是△ABC的外角?说出它们的名称。②∠1、 ∠2是不是△ABC的外角?为什么?练习三角形的外角性质(1)三角形的一个外角等于和它不相邻的两个内角的和。
(2)三角形的一个外角大于与它不相邻的任何一个内角。 在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。思路总结 为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.三角形内角和定理:
三角形的内角和等于1800.返回检验一下自己吧!1、 在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数。解:在△ABC中,
∠A+∠B+∠C=180°,
∠A=80°∴∠B+∠C=100°∵∠B=∠C ∴∠B=∠C=500 ABC2、已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。解:设三个内角度数分别为:x ° ,3x ° ,5x °,
由三角形内角和为180°得x+3x+5x=180解得 x=20所以三个内角度数分别为20°,60°,100°。3.已知:在△ABC中, ∠C=∠ABC=2∠A,BD 是AC边上的高。求∠DBC的度数。 解:设∠A=x°,则∠C=∠ABC=2X0∴x+2x+2x=180 解得:x=36在△BDC中, ∵∠BDC=90° ∴∠DBC=180°-∠BDC- ∠C =180°-90°-72° =18 °∴∠C=72°练习11△ABC中,若∠A+∠B=∠C,则△ABC是()
A、锐角△ B、直角△ C、钝角△ D、等腰△2 一个三角形至少有()
A、一个锐角 B、两个锐角 C、一个钝角 D、一个直角3 如图△ABC中,CD平分∠ACB,DE∥BC, ∠A=70∠B=50,求∠BDC的度数。动脑筋,你能行!练习21如图△ABC中,∠ABC、∠ACB的平分线交于点O, ⑴若∠A=70°,求∠BOC。 ⑵若∠A=X°,求∠BOC。动脑筋,你能行!这节课你有那些收获?
