沪教版五年级下册数学表面积的变化 课件(共15张PPT)
文档属性
| 名称 | 沪教版五年级下册数学表面积的变化 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-18 00:00:00 | ||
图片预览



文档简介
(共15张PPT)
表面积的变化 ③
超市购物
3
1
2
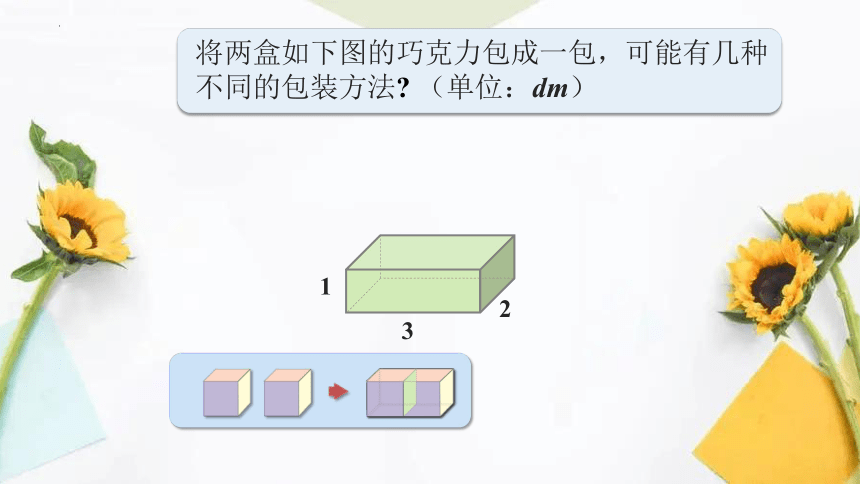
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法 (单位:dm)
3
2
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法 (单位:dm)
1
3
1
2
3
1
2
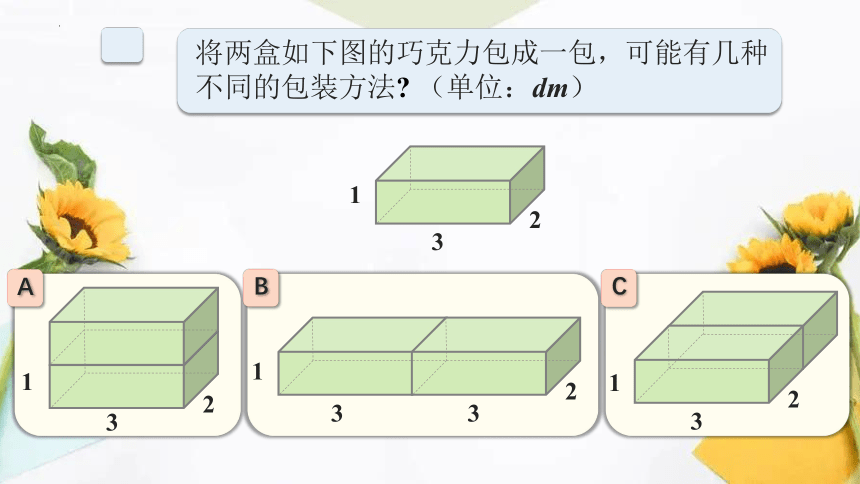
A
3
1
2
3
B
3
1
2
C
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法 (单位:dm)
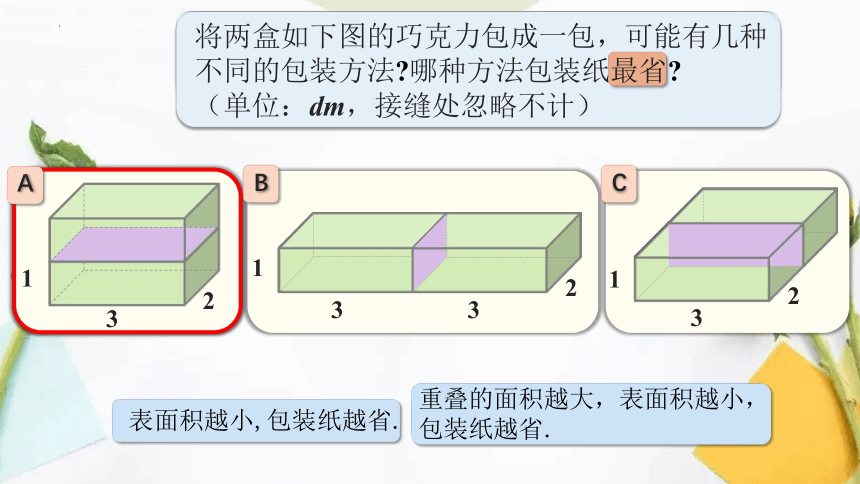
重叠的面积越大,表面积越小,
包装纸越省.
表面积越小,包装纸越省.
3
1
2
A
3
1
2
3
B
3
1
2
C
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
3
1
2
A
3
1
2
3
B
3
1
2
C
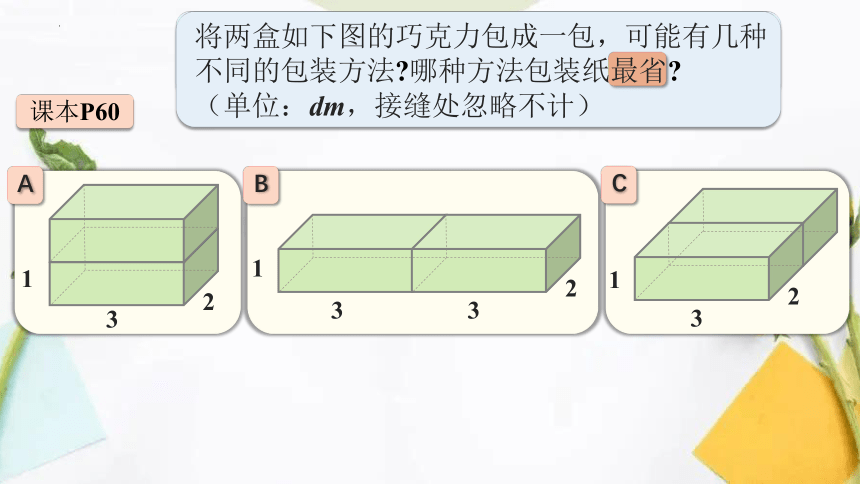
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
课本P60
3
1
2
A
1
拼成后减少的面积:
3×2
2
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×1+3×2+2×1)
= 2×11
= 22 (dm )
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
( )=12 (dm )
×
?
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×2+2×2)
= 2×16
= 32 (dm
C
B
3
1
2
拼成后减少的面积:
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
3
1
2
3
1
2
3
2
拼成的长方体的表面积:
S = 2×(6×1+6×2+2×1)
= 2×20
= 40 (dm )
拼成的长方体的表面积:
S = 2×(3×1+3×4+4×1)
= 2×19
= 38 (dm )
拼成后减少的面积:
拼成后减少的面积:
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×2+2×2)
= 2×16
= 32 (dm )
A
2×1
2
( )=4 (dm )
×
3×1
2
( )=6 (dm )
×
3×2
2
( )=12 (dm )
×
A
B
C
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
两
三
1
2
D
3
3
2
例4
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
三
A
1
1
D
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
三
A
D
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×3+3×2)
= 2×21
= 42 (dm )
1
1
例4
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
三
A
D
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×3+3×2)
= 2×21
= 42 (dm )
3×3+3×2+2×3
3×2+3×3+3×2
例4
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
三
A
D
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
2
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
拼成后减少的面积:
4×(3×2)
= 4×6
= 24 (dm )
例4
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×3+3×2)
= 2×21
= 42 (dm )
图2拼法表面积更小.
试一试
将三个棱长各不相同的正方体拼成一个组合体(如下图),哪种拼法表面积更小
1
2
表面积的变化 ③
超市购物
3
1
2
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法 (单位:dm)
3
2
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法 (单位:dm)
1
3
1
2
3
1
2
A
3
1
2
3
B
3
1
2
C
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法 (单位:dm)
重叠的面积越大,表面积越小,
包装纸越省.
表面积越小,包装纸越省.
3
1
2
A
3
1
2
3
B
3
1
2
C
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
3
1
2
A
3
1
2
3
B
3
1
2
C
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
课本P60
3
1
2
A
1
拼成后减少的面积:
3×2
2
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×1+3×2+2×1)
= 2×11
= 22 (dm )
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
( )=12 (dm )
×
?
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×2+2×2)
= 2×16
= 32 (dm
C
B
3
1
2
拼成后减少的面积:
将两盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
3
1
2
3
1
2
3
2
拼成的长方体的表面积:
S = 2×(6×1+6×2+2×1)
= 2×20
= 40 (dm )
拼成的长方体的表面积:
S = 2×(3×1+3×4+4×1)
= 2×19
= 38 (dm )
拼成后减少的面积:
拼成后减少的面积:
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×2+2×2)
= 2×16
= 32 (dm )
A
2×1
2
( )=4 (dm )
×
3×1
2
( )=6 (dm )
×
3×2
2
( )=12 (dm )
×
A
B
C
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
两
三
1
2
D
3
3
2
例4
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
三
A
1
1
D
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
三
A
D
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×3+3×2)
= 2×21
= 42 (dm )
1
1
例4
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
三
A
D
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×3+3×2)
= 2×21
= 42 (dm )
3×3+3×2+2×3
3×2+3×3+3×2
例4
将 盒如下图的巧克力包成一包,可能有几种不同的包装方法
哪种方法包装纸最省
(单位:dm,接缝处忽略不计)
三
A
D
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
2
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×3+3×2+2×3)
= 2×21
= 42 (dm )
拼成后减少的面积:
4×(3×2)
= 4×6
= 24 (dm )
例4
拼成的长方体的表面积:
S = 2 (ah+ab+bh)
= 2×(3×2+3×3+3×2)
= 2×21
= 42 (dm )
图2拼法表面积更小.
试一试
将三个棱长各不相同的正方体拼成一个组合体(如下图),哪种拼法表面积更小
1
2
