一次函数的图像和性质的课件
文档属性
| 名称 | 一次函数的图像和性质的课件 |  | |
| 格式 | zip | ||
| 文件大小 | 834.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-14 16:10:05 | ||
图片预览




文档简介
课件45张PPT。一次函数的图像和性质
xy0提问复习,引入新课1、什么叫正比例函数、一次函数?它们之间有什么关系?2、正比例函数的图象是什么形状? 一般地,形如 的函数,叫做正比例函数; 一般地,形如 的函数,叫做一次函数。 当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。正比例函数的图象是( )y=kx(k是常数,k≠0)y=kx+b(k,b是常数,k≠0)y=kx经过原点的一条直线经过一、三象限
y随x增大而增大经过二、四象限
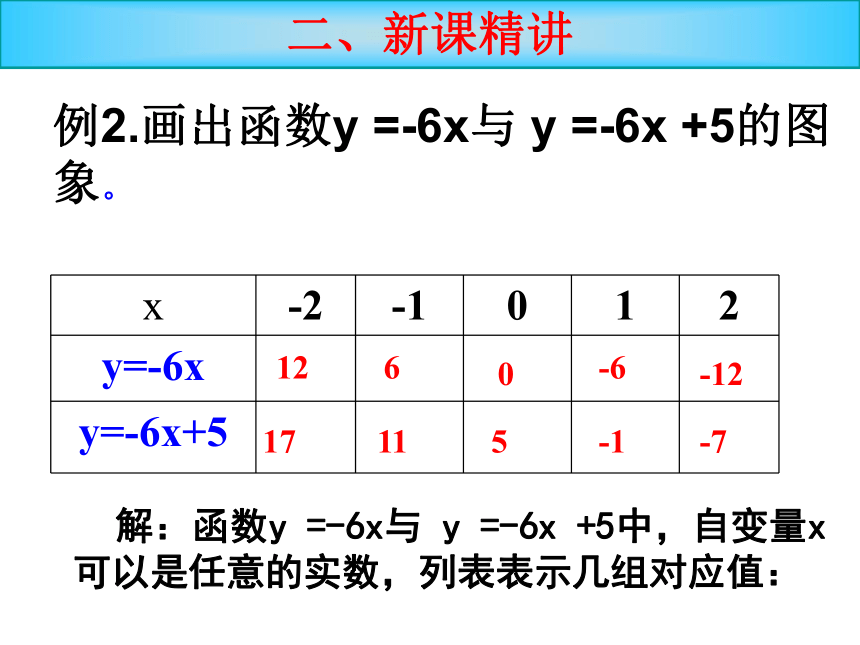
y随x增大而减小3、正比例函数 y=kx(k是常数,k≠0)中,
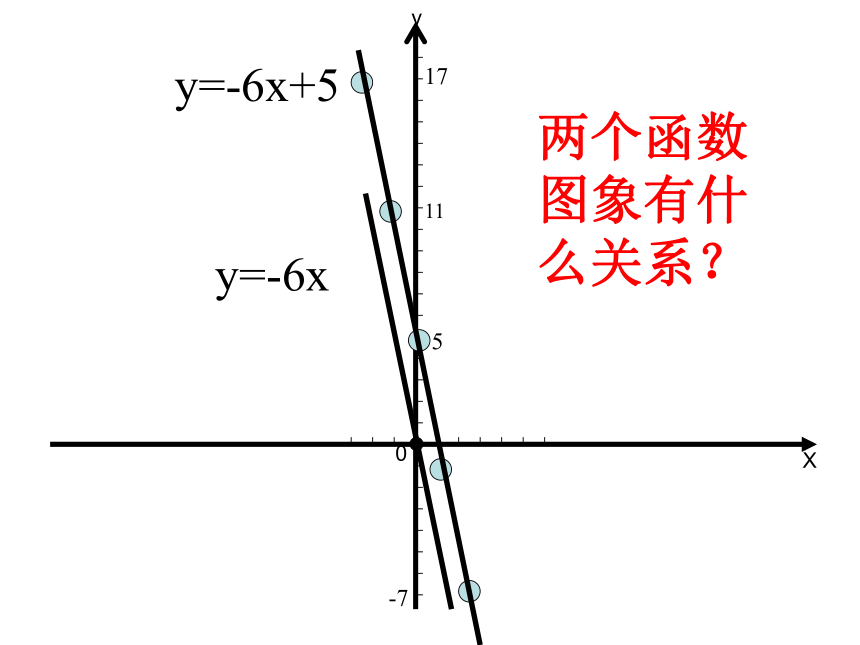
k的正负对函数图象有什么影响?yx图像必经过(0,0)和(1,k)这两个点60-6-121217115-1-7例2.画出函数y =-6x与 y =-6x +5的图象。
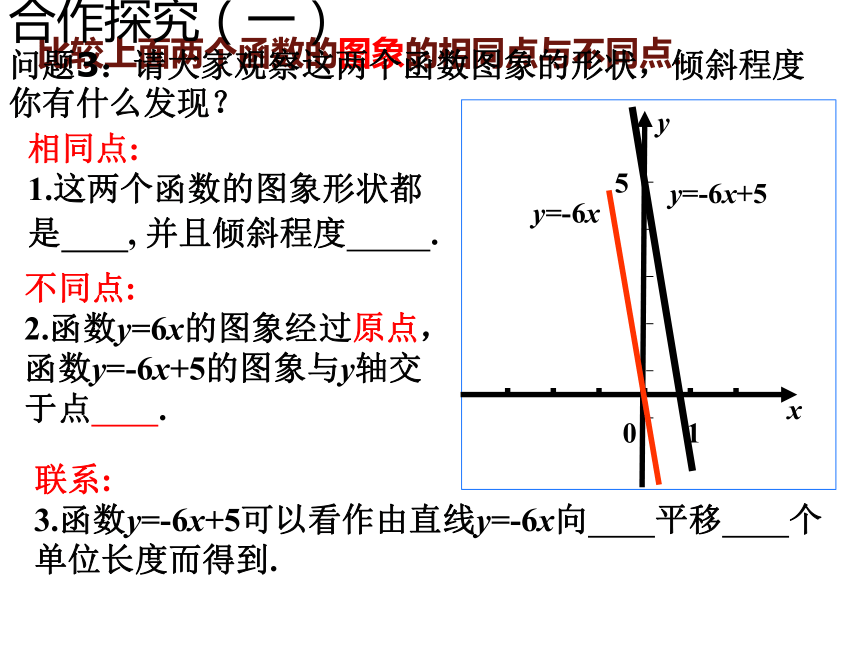
解:函数y =-6x与 y =-6x +5中,自变量x 可以是任意的实数,列表表示几组对应值:二、新课精讲17115-7y=-6xy=-6x+5两个函数图象有什么关系?0Xyxy015y=-6x+5y=-6x不同点:
2.函数y=6x的图象经过原点,函数y=-6x+5的图象与y轴交于点 .比较上面两个函数的图象的相同点与不同点.相同点:
1.这两个函数的图象形状都是 , 并且倾斜程度 .联系:
3.函数y=-6x+5可以看作由直线y=-6x向 平移 个单位长度而得到.问题3:请大家观察这两个函数图象的形状,倾斜程度你有什么发现?合作探究(一)比较两个函数解析式,你能说出这两个函数图象有平移关系的道理吗?y=-6x+5y=-6x联系:
3.对于自变量x的任一值,这两个函数相应的y值总相差 。相同点:
1.这两个函数解析式都是自变量x的 (常数)倍,与一个常数的和。不同点:
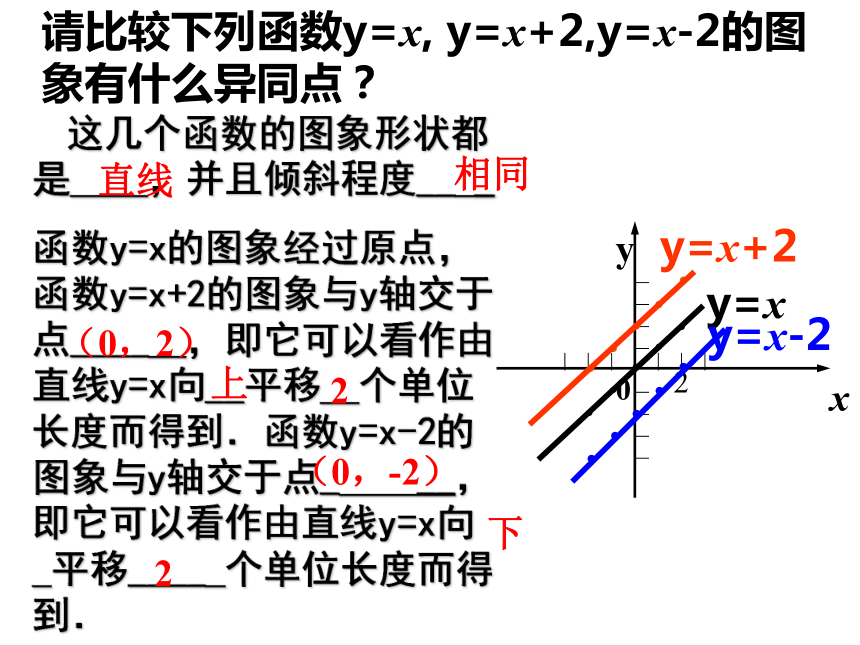
2.这两个函数解析式仅在 有区别。.......请比较下列函数y=x, y=x+2,y=x-2的图象有什么异同点?....y=x....y=x+2y=x-2 这几个函数的图象形状都是 ,并且倾斜程度__ _
函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____ 个单位长度而得到.直线相同(0,2)上2(0,-2)下2例1 在同一平面直角坐标系中画出下列
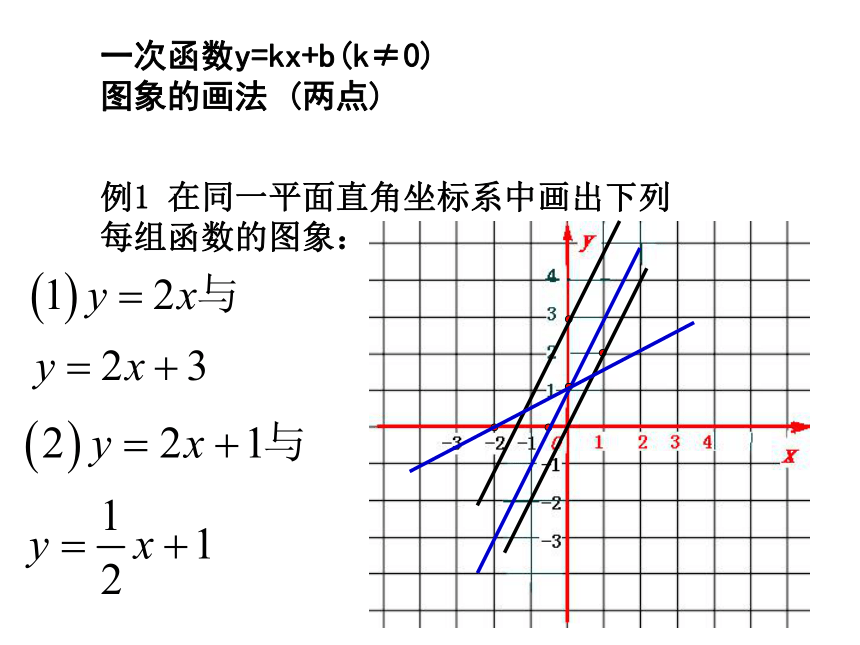
每组函数的图象: 一次函数y=kx+b(k≠0)
图象的画法 (两点)比较下列一对一次函数的图象有什么共同点,
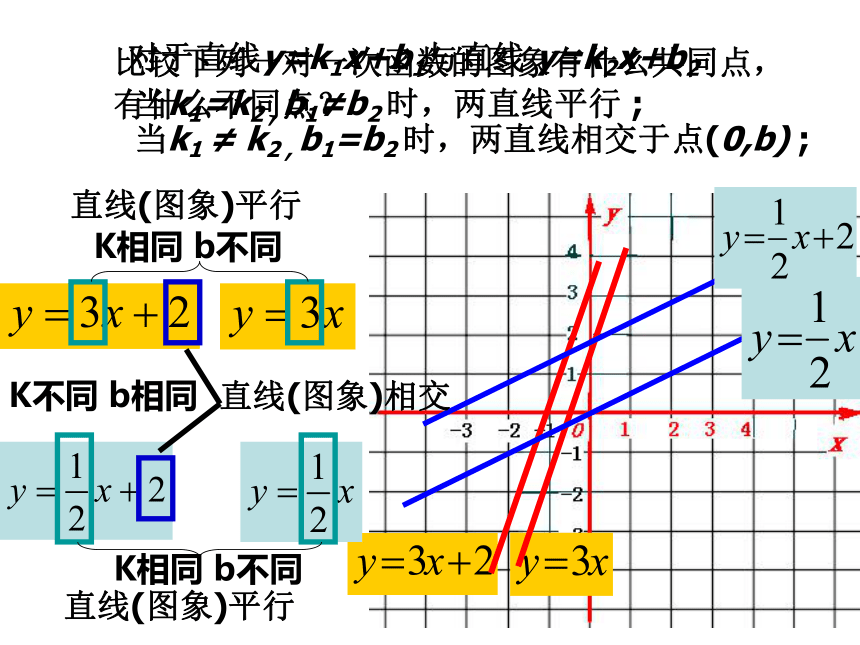
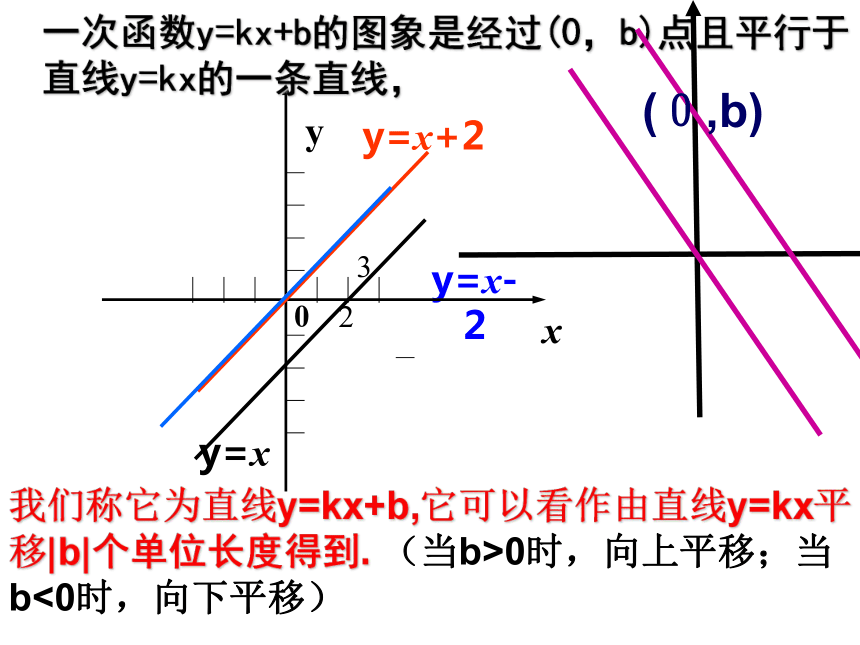
有什么不同点? K相同 b不同K相同 b不同直线(图象)平行直线(图象)平行对于直线y=k1x+b1与直线 y=k2x+b2当k1=k2 , b1≠b2 时,两直线平行 ;K不同 b相同直线(图象)相交当k1 ≠ k2 , b1=b2 时,两直线相交于点(0,b) ;y=xy=x+2y=x-2y30一次函数y=kx+b的图象是经过(0,b)点且平行于
直线y=kx的一条直线,
我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到. (当b>0时,向上平移;当b<0时,向下平移)
(0,b)推广:(1)所有一次函数y=kx+b的图象都是________(2)直线 y=kx+b与直线y=kx__________;(3)直线 y=kx+b可以看作由直线y=kx _________ 而得到一条直线;互相平行平移 个单位当b>0,向上平移b个单位;
当b<0,向下平移b个单位。其中,b叫做直线 y=kx+b在y轴上的截距。 (1)直线y=2x-3可以由直线y=2x经过____________ 而得到;
直线y=-3x+2可以由直线y=-3x经过_______________而得到;
直线y=x+2可以由直线y=x-3经过_________________而得到.
向下平移3个单位向上平移2个单位向下平移5个单位(2)直线y=2x+5与直线y=-3x+5都经过轴上的同一点(___,___).
(3)将直线y=-2x-1向上平移3个单位,得到的直线是______.
0 5y=-2x+2(4)直线y=3x-2可由直线y=3x向 平移 单位得到。下2(5)直线y=x+2可由直线y=x-1向 平移 单位得到。上3(6)函数y=2x - 4与y轴的交点为 ( ),与x轴交于( )0,-42, 0选取适当两点作图:y=kx﹙k≠0﹚(1,k+b)常取点 ﹙0,0﹚ ﹙1,,k﹚常取点用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.2、用两点法画一次函数图像实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.0
0
-1
0
0.5012经过(0,-1)和(0.5,0)两点经过(0,1)和(2,0)两点y=2x-1y=-0.5x+1画出一次函数 的图象 31y30X观察分析: 自变量x由___到___函数y的值从___到___大小小大函数y=3x-2的图象是否也有这种现象 y随x的增大而增大,
这时函数的图象从左到右上升; 结论的图象 观察分析: 自变量x由___到___函数y的值从___到___大小小大y随x的增大而减小,
这时函数的图象从左到右下降; 结论一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 减小下降增大上升一次函数 y=kx+b k 决定直线的倾斜程度和方向当k>0时,y随x的增大而增大2.当k<0时,y随x的增大而减少3.当 k 相等时,直线平行4.当 |k| 越大时,图象越靠近y轴体验:在同一坐标系中用两点法画出函数
y=x+1,
y=-x+1,
y=2x+1
y=-2x+1的图象.y=x+1y=-x+1y=2x+1y=-2x+13、学习一次函数性质一次函数 y=kx+b b 决定直线与y轴交点位置当b>0时,直线交于y正半轴4.当 b 相等时,直线交于y轴上同一点2.当b<0时,直线交于y负半轴3.当b = 0时,直线交于坐标原点xx -5 -4 -3 -2 -154321-1 0-2-3-4-5 1 2 3 4 5xy正撇负捺;上加下减1、看图象,确定一次函数y=kx+b(k≠0)中k,b的符号。k<0
b<0k>0
b>0
k<0
b=02、下列函数草图是否正确,如果错误,应如何画?为什么?y=1.5xyx0y=-2x+3yx0y=kx+b﹙k>0,b<0﹚yx0xy0正确为:xy0正确为:y=kx+b﹙k>0,b<0﹚正确为:y=1.5xxy03.下列一次函数中,y的值随x的增大
而减小的有________。(3)(4)(2) (4)(1) y=10x-9(2) y=-0.3x+24.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )(A)(B)(C)(D)B
5、已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )B(6)下列函数中,y的值随x值的增大而增大的函数是________. A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2C(7)对于函数y=5x+6,y的值随x的值减小而______。(8)函数y=2x-1经过 象限减少一、三、四
9、已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:(4)函数的图象过原点。(3)函数的图象过第二、三、四象限;(2)函数图象与y 轴的负半轴相交;(1)函数值y 随x的增大而增大;(10)已知一次函数y=(1-2k)x+k的函数值y随x的增大而增大,且图象经过一、二、三象限,则k的取值范围是__________.0﹤k﹤1/211. 直线y=2x-3与x轴交点坐标为______;与y轴的交点坐标为______;图象经过________象限,y随x的增大而____
12.若直线平行于直线y=-3x-5,则k= ______ .(3/2,0)(0,-3)一、二、四增大-3
13、一个函数的图象经过点(1,2),
且y随x的增大而增大而这个函数的解析式是________________(只需写一个) y = 3x-114、直线y=kx+b与直线y=5x+2平行,与y轴的交点为(0,-7),则解析式为_______.y=5x-7例 一次函数y=kx+b的图象不经过第二象限,则 k、b的符号是:
解析:∵图象不过第二象限 ∴图象必过一、三象限
∴k > 0
由于图象不过第二象限,说明图象可能过 第四象限
∴b≤0
∴k > 0 b ≤0或原点
15、如图,在同一坐标系中,关于x的一次函数y = x+ b与 y = bx+1的图象只可能是( )C16、一次函数y=kx-k的图象可能是( )ABCDC17、如图所示,不可能是关于x的一次函数y=mx-(m-3)的图像是( )
CD-3y12 y2 19、对于一次函数y=(a+4)x+2a-1,如果y随x的增大而增大,且它的图与y轴的交点在x轴的下方,试求a的取值范围解: ∵ y随x的增大而增大∴a+4 >0∴a>-4∵图象与y轴的交点在x轴的下方∴ 2a-1 0< ∴a< 1/2
∴ -4 2、一次函数y=kx+b的图象经过点A(0,4)且与两坐标轴围成的三角形的面积为8,求这个一次函数的关系式。3:如图,一次函数y= kx + b 的图象过点A(3,0).与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式 例3 如图所示,一次函数的图象与x轴、y轴分别相交于A,B两点,如果A点的坐标为A(2,0),且OA=OB,试求一次函数的解析式。解:设解析式∵OA=OB,A(2,0)∴B(0,-2)∴一次函数的关系式:一次函数y=kx+b(k≠0)的自变量的取值范围是-3≤x≤6,相应函数值的范围是-5≤y≤-2,求这个函数的解析式.
xy0提问复习,引入新课1、什么叫正比例函数、一次函数?它们之间有什么关系?2、正比例函数的图象是什么形状? 一般地,形如 的函数,叫做正比例函数; 一般地,形如 的函数,叫做一次函数。 当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。正比例函数的图象是( )y=kx(k是常数,k≠0)y=kx+b(k,b是常数,k≠0)y=kx经过原点的一条直线经过一、三象限
y随x增大而增大经过二、四象限
y随x增大而减小3、正比例函数 y=kx(k是常数,k≠0)中,
k的正负对函数图象有什么影响?yx图像必经过(0,0)和(1,k)这两个点60-6-121217115-1-7例2.画出函数y =-6x与 y =-6x +5的图象。
解:函数y =-6x与 y =-6x +5中,自变量x 可以是任意的实数,列表表示几组对应值:二、新课精讲17115-7y=-6xy=-6x+5两个函数图象有什么关系?0Xyxy015y=-6x+5y=-6x不同点:
2.函数y=6x的图象经过原点,函数y=-6x+5的图象与y轴交于点 .比较上面两个函数的图象的相同点与不同点.相同点:
1.这两个函数的图象形状都是 , 并且倾斜程度 .联系:
3.函数y=-6x+5可以看作由直线y=-6x向 平移 个单位长度而得到.问题3:请大家观察这两个函数图象的形状,倾斜程度你有什么发现?合作探究(一)比较两个函数解析式,你能说出这两个函数图象有平移关系的道理吗?y=-6x+5y=-6x联系:
3.对于自变量x的任一值,这两个函数相应的y值总相差 。相同点:
1.这两个函数解析式都是自变量x的 (常数)倍,与一个常数的和。不同点:
2.这两个函数解析式仅在 有区别。.......请比较下列函数y=x, y=x+2,y=x-2的图象有什么异同点?....y=x....y=x+2y=x-2 这几个函数的图象形状都是 ,并且倾斜程度__ _
函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点____ ,即它可以看作由直线y=x向__平移 个单位长度而得到.函数y=x-2的图象与y轴交于点_ __,即它可以看作由直线y=x向 平移____ 个单位长度而得到.直线相同(0,2)上2(0,-2)下2例1 在同一平面直角坐标系中画出下列
每组函数的图象: 一次函数y=kx+b(k≠0)
图象的画法 (两点)比较下列一对一次函数的图象有什么共同点,
有什么不同点? K相同 b不同K相同 b不同直线(图象)平行直线(图象)平行对于直线y=k1x+b1与直线 y=k2x+b2当k1=k2 , b1≠b2 时,两直线平行 ;K不同 b相同直线(图象)相交当k1 ≠ k2 , b1=b2 时,两直线相交于点(0,b) ;y=xy=x+2y=x-2y30一次函数y=kx+b的图象是经过(0,b)点且平行于
直线y=kx的一条直线,
我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到. (当b>0时,向上平移;当b<0时,向下平移)
(0,b)推广:(1)所有一次函数y=kx+b的图象都是________(2)直线 y=kx+b与直线y=kx__________;(3)直线 y=kx+b可以看作由直线y=kx _________ 而得到一条直线;互相平行平移 个单位当b>0,向上平移b个单位;
当b<0,向下平移b个单位。其中,b叫做直线 y=kx+b在y轴上的截距。 (1)直线y=2x-3可以由直线y=2x经过____________ 而得到;
直线y=-3x+2可以由直线y=-3x经过_______________而得到;
直线y=x+2可以由直线y=x-3经过_________________而得到.
向下平移3个单位向上平移2个单位向下平移5个单位(2)直线y=2x+5与直线y=-3x+5都经过轴上的同一点(___,___).
(3)将直线y=-2x-1向上平移3个单位,得到的直线是______.
0 5y=-2x+2(4)直线y=3x-2可由直线y=3x向 平移 单位得到。下2(5)直线y=x+2可由直线y=x-1向 平移 单位得到。上3(6)函数y=2x - 4与y轴的交点为 ( ),与x轴交于( )0,-42, 0选取适当两点作图:y=kx﹙k≠0﹚(1,k+b)常取点 ﹙0,0﹚ ﹙1,,k﹚常取点用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.2、用两点法画一次函数图像实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.0
0
-1
0
0.5012经过(0,-1)和(0.5,0)两点经过(0,1)和(2,0)两点y=2x-1y=-0.5x+1画出一次函数 的图象 31y30X观察分析: 自变量x由___到___函数y的值从___到___大小小大函数y=3x-2的图象是否也有这种现象 y随x的增大而增大,
这时函数的图象从左到右上升; 结论的图象 观察分析: 自变量x由___到___函数y的值从___到___大小小大y随x的增大而减小,
这时函数的图象从左到右下降; 结论一次函数y=kx+b有下列性质:
?
(1) 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____ ;
?
(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____. 减小下降增大上升一次函数 y=kx+b k 决定直线的倾斜程度和方向当k>0时,y随x的增大而增大2.当k<0时,y随x的增大而减少3.当 k 相等时,直线平行4.当 |k| 越大时,图象越靠近y轴体验:在同一坐标系中用两点法画出函数
y=x+1,
y=-x+1,
y=2x+1
y=-2x+1的图象.y=x+1y=-x+1y=2x+1y=-2x+13、学习一次函数性质一次函数 y=kx+b b 决定直线与y轴交点位置当b>0时,直线交于y正半轴4.当 b 相等时,直线交于y轴上同一点2.当b<0时,直线交于y负半轴3.当b = 0时,直线交于坐标原点xx -5 -4 -3 -2 -154321-1 0-2-3-4-5 1 2 3 4 5xy正撇负捺;上加下减1、看图象,确定一次函数y=kx+b(k≠0)中k,b的符号。k<0
b<0k>0
b>0
k<0
b=02、下列函数草图是否正确,如果错误,应如何画?为什么?y=1.5xyx0y=-2x+3yx0y=kx+b﹙k>0,b<0﹚yx0xy0正确为:xy0正确为:y=kx+b﹙k>0,b<0﹚正确为:y=1.5xxy03.下列一次函数中,y的值随x的增大
而减小的有________。(3)(4)(2) (4)(1) y=10x-9(2) y=-0.3x+24.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )(A)(B)(C)(D)B
5、已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )B(6)下列函数中,y的值随x值的增大而增大的函数是________. A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2C(7)对于函数y=5x+6,y的值随x的值减小而______。(8)函数y=2x-1经过 象限减少一、三、四
9、已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:(4)函数的图象过原点。(3)函数的图象过第二、三、四象限;(2)函数图象与y 轴的负半轴相交;(1)函数值y 随x的增大而增大;(10)已知一次函数y=(1-2k)x+k的函数值y随x的增大而增大,且图象经过一、二、三象限,则k的取值范围是__________.0﹤k﹤1/211. 直线y=2x-3与x轴交点坐标为______;与y轴的交点坐标为______;图象经过________象限,y随x的增大而____
12.若直线平行于直线y=-3x-5,则k= ______ .(3/2,0)(0,-3)一、二、四增大-3
13、一个函数的图象经过点(1,2),
且y随x的增大而增大而这个函数的解析式是________________(只需写一个) y = 3x-114、直线y=kx+b与直线y=5x+2平行,与y轴的交点为(0,-7),则解析式为_______.y=5x-7例 一次函数y=kx+b的图象不经过第二象限,则 k、b的符号是:
解析:∵图象不过第二象限 ∴图象必过一、三象限
∴k > 0
由于图象不过第二象限,说明图象可能过 第四象限
∴b≤0
∴k > 0 b ≤0或原点
15、如图,在同一坐标系中,关于x的一次函数y = x+ b与 y = bx+1的图象只可能是( )C16、一次函数y=kx-k的图象可能是( )ABCDC17、如图所示,不可能是关于x的一次函数y=mx-(m-3)的图像是( )
CD-3y12 y2 19、对于一次函数y=(a+4)x+2a-1,如果y随x的增大而增大,且它的图与y轴的交点在x轴的下方,试求a的取值范围解: ∵ y随x的增大而增大∴a+4 >0∴a>-4∵图象与y轴的交点在x轴的下方∴ 2a-1 0< ∴a< 1/2
∴ -4 2、一次函数y=kx+b的图象经过点A(0,4)且与两坐标轴围成的三角形的面积为8,求这个一次函数的关系式。3:如图,一次函数y= kx + b 的图象过点A(3,0).与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式 例3 如图所示,一次函数的图象与x轴、y轴分别相交于A,B两点,如果A点的坐标为A(2,0),且OA=OB,试求一次函数的解析式。解:设解析式∵OA=OB,A(2,0)∴B(0,-2)∴一次函数的关系式:一次函数y=kx+b(k≠0)的自变量的取值范围是-3≤x≤6,相应函数值的范围是-5≤y≤-2,求这个函数的解析式.
