【同步培优微专题】专题9 线段计算——整体思想(含答案)
文档属性
| 名称 | 【同步培优微专题】专题9 线段计算——整体思想(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 159.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-20 21:12:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题 线段计算——整体思想
一、理解中点的含义
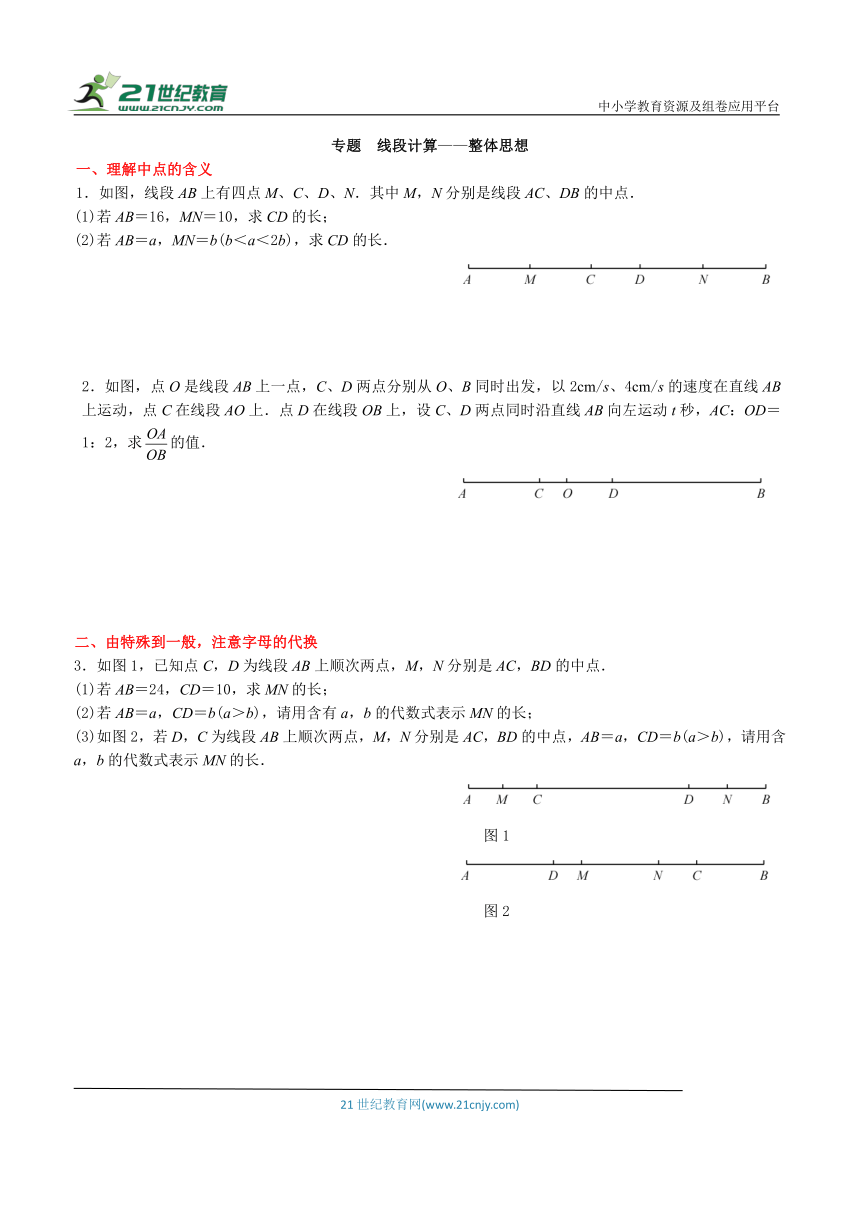
1.如图,线段AB上有四点M、C、D、N.其中M,N分别是线段AC、DB的中点.
(1)若AB=16,MN=10,求CD的长;
(2)若AB=a,MN=b(b<a<2b),求CD的长.
2.如图,点O是线段AB上一点,C、D两点分别从O、B同时出发,以2cm/s、4cm/s的速度在直线AB上运动,点C在线段AO上.点D在线段OB上,设C、D两点同时沿直线AB向左运动t秒,AC:OD=1:2,求的值.
二、由特殊到一般,注意字母的代换
3.如图1,已知点C,D为线段AB上顺次两点,M,N分别是AC,BD的中点.
(1)若AB=24,CD=10,求MN的长;
(2)若AB=a,CD=b(a>b),请用含有a,b的代数式表示MN的长;
(3)如图2,若D,C为线段AB上顺次两点,M,N分别是AC,BD的中点,AB=a,CD=b(a>b),请用含a,b的代数式表示MN的长.
图1
图2
专题 线段计算——整体思想
一、理解中点的含义
1.如图,线段AB上有四点M、C、D、N.其中M,N分别是线段AC、DB的中点.
(1)若AB=16,MN=10,求CD的长;
(2)若AB=a,MN=b(b<a<2b),求CD的长.
答案:(1)AM+BN=16-10=6,CD=MN-6=4;
(2)AM+BN=a-b,MC+DN=a-b,CD=MN-(MC+DN)=b-(a-b)=2b-a.
2.如图,点O是线段AB上一点,C、D两点分别从O、B同时出发,以2cm/s、4cm/s的速度在直线AB上运动,点C在线段AO上.点D在线段OB上,设C、D两点同时沿直线AB向左运动t秒,AC:OD=1:2,求的值.
答案:设AC=x,OD=2x,又OC=2t,DB=4t,∴OA=x+2t,OB=2x+4t,∴.
二、由特殊到一般,注意字母的代换
3.如图1,已知点C,D为线段AB上顺次两点,M,N分别是AC,BD的中点.
(1)若AB=24,CD=10,求MN的长;
(2)若AB=a,CD=b(a>b),请用含有a,b的代数式表示MN的长;
(3)如图2,若D,C为线段AB上顺次两点,M,N分别是AC,BD的中点,AB=a,CD=b(a>b),请用含a,b的代数式表示MN的长.
图1
图2
答案:(1)MN=17;
(2)由(1)得AC+BD=AB-CD=a-b,则CM+DN=,
故MN=CD+CM+DN==;
(3)由题意得:AM+MN+NB=AB=a,因为M,N分别是AC,BD中点,
所以AM=MC,BN=DN,所以MC+MN+DN=AB=a,
又因为MC=MN+NC,DN=DM+MN,所以3MN+NC+DM=a.
因为DM+MN+NC=CD=b,所以CD+2MN=b+2MN=a.所以.
21世纪教育网(www.21cnjy.com)
专题 线段计算——整体思想
一、理解中点的含义
1.如图,线段AB上有四点M、C、D、N.其中M,N分别是线段AC、DB的中点.
(1)若AB=16,MN=10,求CD的长;
(2)若AB=a,MN=b(b<a<2b),求CD的长.
2.如图,点O是线段AB上一点,C、D两点分别从O、B同时出发,以2cm/s、4cm/s的速度在直线AB上运动,点C在线段AO上.点D在线段OB上,设C、D两点同时沿直线AB向左运动t秒,AC:OD=1:2,求的值.
二、由特殊到一般,注意字母的代换
3.如图1,已知点C,D为线段AB上顺次两点,M,N分别是AC,BD的中点.
(1)若AB=24,CD=10,求MN的长;
(2)若AB=a,CD=b(a>b),请用含有a,b的代数式表示MN的长;
(3)如图2,若D,C为线段AB上顺次两点,M,N分别是AC,BD的中点,AB=a,CD=b(a>b),请用含a,b的代数式表示MN的长.
图1
图2
专题 线段计算——整体思想
一、理解中点的含义
1.如图,线段AB上有四点M、C、D、N.其中M,N分别是线段AC、DB的中点.
(1)若AB=16,MN=10,求CD的长;
(2)若AB=a,MN=b(b<a<2b),求CD的长.
答案:(1)AM+BN=16-10=6,CD=MN-6=4;
(2)AM+BN=a-b,MC+DN=a-b,CD=MN-(MC+DN)=b-(a-b)=2b-a.
2.如图,点O是线段AB上一点,C、D两点分别从O、B同时出发,以2cm/s、4cm/s的速度在直线AB上运动,点C在线段AO上.点D在线段OB上,设C、D两点同时沿直线AB向左运动t秒,AC:OD=1:2,求的值.
答案:设AC=x,OD=2x,又OC=2t,DB=4t,∴OA=x+2t,OB=2x+4t,∴.
二、由特殊到一般,注意字母的代换
3.如图1,已知点C,D为线段AB上顺次两点,M,N分别是AC,BD的中点.
(1)若AB=24,CD=10,求MN的长;
(2)若AB=a,CD=b(a>b),请用含有a,b的代数式表示MN的长;
(3)如图2,若D,C为线段AB上顺次两点,M,N分别是AC,BD的中点,AB=a,CD=b(a>b),请用含a,b的代数式表示MN的长.
图1
图2
答案:(1)MN=17;
(2)由(1)得AC+BD=AB-CD=a-b,则CM+DN=,
故MN=CD+CM+DN==;
(3)由题意得:AM+MN+NB=AB=a,因为M,N分别是AC,BD中点,
所以AM=MC,BN=DN,所以MC+MN+DN=AB=a,
又因为MC=MN+NC,DN=DM+MN,所以3MN+NC+DM=a.
因为DM+MN+NC=CD=b,所以CD+2MN=b+2MN=a.所以.
21世纪教育网(www.21cnjy.com)
