第二十九章 投影与视图 基础复习卷(含答案)
文档属性
| 名称 | 第二十九章 投影与视图 基础复习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 13:16:28 | ||
图片预览

文档简介
第二十九章 投影与视图 基础复习卷
知识点一 平行投影
1.下列四幅图形中,表示两棵树在同一时刻阳光下的影子的图形可能是 ( )
2.小明身高 1.5m ,经太阳光照射后在地面的影长为 2m ,若此时测得一塔在同一地面的影长为60 m,则塔高为 m.
3.小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图表示为小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子;
(2)若知小明身高是 1.60 m,小明与小丽间的距离为 2m ,而小丽的影子长为 1.75 m,求小丽的身高.
知识点二 中心投影
4.如图,晚上小亮在路灯下散步,他从 A 处向着路灯灯柱方向径直走到 B处,这一过程中他在该路灯灯光下的影子 ( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变知
5.确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
中小学教育资源及组卷应用平台
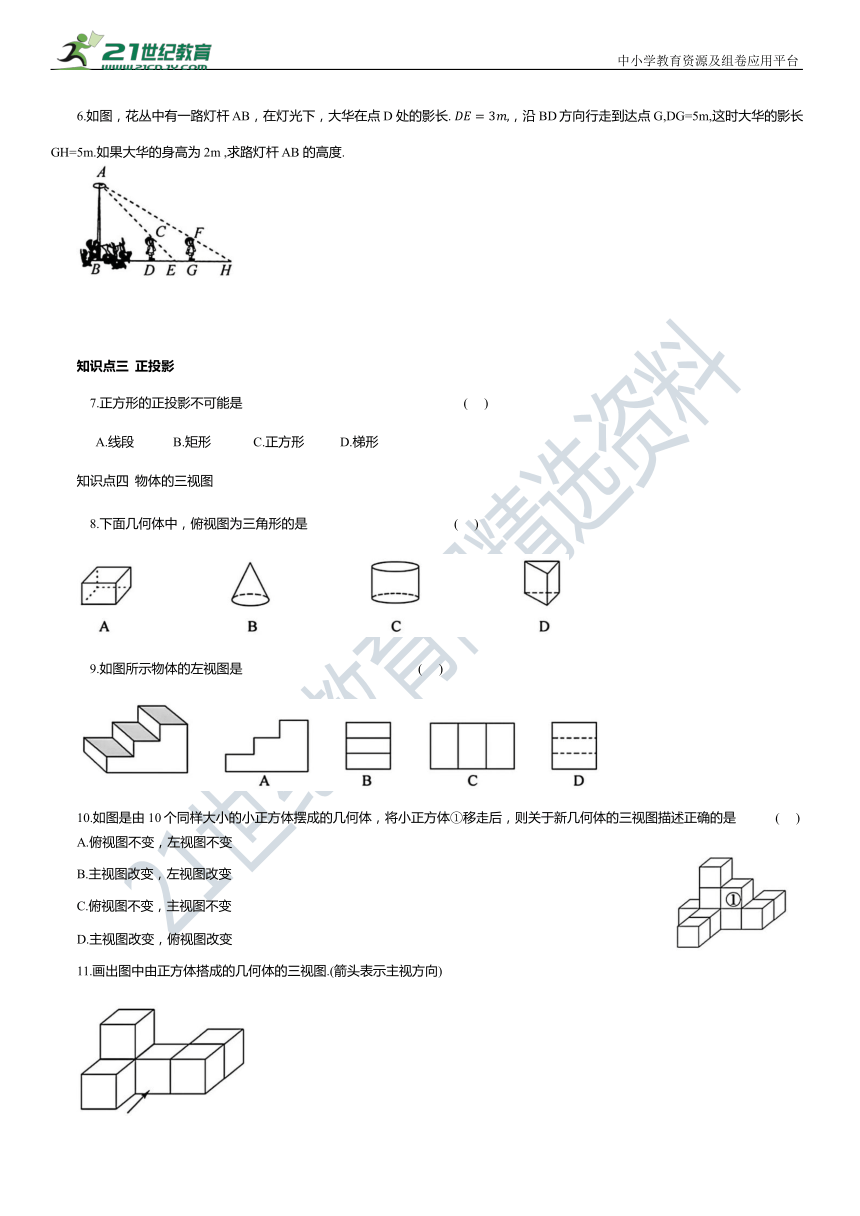
6.如图,花丛中有一路灯杆 AB,在灯光下,大华在点 D 处的影长. ,沿 BD方向行走到达点G,DG=5m,这时大华的影长GH=5m.如果大华的身高为 2m ,求路灯杆 AB 的高度.
知识点三 正投影
7.正方形的正投影不可能是 ( )
A.线段 B.矩形 C.正方形 D.梯形
知识点四 物体的三视图
8.下面几何体中,俯视图为三角形的是 ( )
9.如图所示物体的左视图是 ( )
10.如图是由 10个同样大小的小正方体摆成的几何体,将小正方体①移走后,则关于新几何体的三视图描述正确的是 ( )
A.俯视图不变,左视图不变
B.主视图改变,左视图改变
C.俯视图不变,主视图不变
D.主视图改变,俯视图改变
11.画出图中由正方体搭成的几何体的三视图.(箭头表示主视方向)
知识点五 由三视图确定几何体的形状
12.某个几何体的三视图如图所示,该几何体是 ( )
13.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是 ( )
A.4 B.5 C.6 D.9
14.由若干个大小形状完全相同的小立方块所搭几何体的俯视图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是 ( )
15.若干桶方便面摆放在桌子上,如图所示是它的三视图,则这一堆方便面共有 ( )
A.5 桶 B.6 桶 C.9桶 D.12 桶
知识点六 由三视图计算几何体的表面积或体积
16.图2 是图 1中长方体的三视图,若用S 表示面积,且 则Sm = ( )
17.一个圆柱体的三视图如图所示,若其俯视图为圆,则这个圆柱体的体积为 ( )
A.24
B.24π
C.96
D.96π
18.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点 B 出发,沿表面爬到 AC的中点D.请求出蚂蚁爬行的最短路程.
19.由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置上小正方体的个数.
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(上、下底面均不喷色),需要喷色的面积为 ;
(3)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
20.一个礼品包装盒的三视图如图,画出它的展开图,并计算它的表面积.
一、1. C 2. D 3. B 4. D 5. B 6. D 7. D 8. A
二、9. -1 12.11 3. 14.566
三、15.(1)1
16.解:(1)∵∠C=90°,AB=13,BC=5,∴AC=√AB -BC = -5 =12,
17.(1)在 Rt△ADE中,由 得 AD=10,则
由 BD平分∠ABC,DE⊥AB,∠C=90°,可知(
(2)由 AD=10,CD=8,得 AC=18.
在 Rt△ACB中, 得 AB=30.
由勾股定理得 BC=24.
所以在 Rt△DBC中,
18.解:在 Rt△ACE中,
在 Rt△BCD 中,∵∠ ︾105.7,
20.解:图略,由三视图可知这个礼品包装盒为正六棱柱,它的表面积为
知识点一 平行投影
1.下列四幅图形中,表示两棵树在同一时刻阳光下的影子的图形可能是 ( )
2.小明身高 1.5m ,经太阳光照射后在地面的影长为 2m ,若此时测得一塔在同一地面的影长为60 m,则塔高为 m.
3.小明和小丽在操场上玩耍,小丽突然高兴地对小明说:“我踩到你的‘脑袋’了.”如图表示为小明和小丽的位置.
(1)请画出此时小丽在阳光下的影子;
(2)若知小明身高是 1.60 m,小明与小丽间的距离为 2m ,而小丽的影子长为 1.75 m,求小丽的身高.
知识点二 中心投影
4.如图,晚上小亮在路灯下散步,他从 A 处向着路灯灯柱方向径直走到 B处,这一过程中他在该路灯灯光下的影子 ( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变知
5.确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
中小学教育资源及组卷应用平台
6.如图,花丛中有一路灯杆 AB,在灯光下,大华在点 D 处的影长. ,沿 BD方向行走到达点G,DG=5m,这时大华的影长GH=5m.如果大华的身高为 2m ,求路灯杆 AB 的高度.
知识点三 正投影
7.正方形的正投影不可能是 ( )
A.线段 B.矩形 C.正方形 D.梯形
知识点四 物体的三视图
8.下面几何体中,俯视图为三角形的是 ( )
9.如图所示物体的左视图是 ( )
10.如图是由 10个同样大小的小正方体摆成的几何体,将小正方体①移走后,则关于新几何体的三视图描述正确的是 ( )
A.俯视图不变,左视图不变
B.主视图改变,左视图改变
C.俯视图不变,主视图不变
D.主视图改变,俯视图改变
11.画出图中由正方体搭成的几何体的三视图.(箭头表示主视方向)
知识点五 由三视图确定几何体的形状
12.某个几何体的三视图如图所示,该几何体是 ( )
13.由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是 ( )
A.4 B.5 C.6 D.9
14.由若干个大小形状完全相同的小立方块所搭几何体的俯视图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是 ( )
15.若干桶方便面摆放在桌子上,如图所示是它的三视图,则这一堆方便面共有 ( )
A.5 桶 B.6 桶 C.9桶 D.12 桶
知识点六 由三视图计算几何体的表面积或体积
16.图2 是图 1中长方体的三视图,若用S 表示面积,且 则Sm = ( )
17.一个圆柱体的三视图如图所示,若其俯视图为圆,则这个圆柱体的体积为 ( )
A.24
B.24π
C.96
D.96π
18.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点 B 出发,沿表面爬到 AC的中点D.请求出蚂蚁爬行的最短路程.
19.由一些大小相同,棱长为1的小正方体搭成的几何体的俯视图如图所示,数字表示该位置上小正方体的个数.
(1)请画出它的主视图和左视图;
(2)给这个几何体喷上颜色(上、下底面均不喷色),需要喷色的面积为 ;
(3)在不改变主视图和俯视图的情况下,最多可添加 块小正方体.
20.一个礼品包装盒的三视图如图,画出它的展开图,并计算它的表面积.
一、1. C 2. D 3. B 4. D 5. B 6. D 7. D 8. A
二、9. -1 12.11 3. 14.566
三、15.(1)1
16.解:(1)∵∠C=90°,AB=13,BC=5,∴AC=√AB -BC = -5 =12,
17.(1)在 Rt△ADE中,由 得 AD=10,则
由 BD平分∠ABC,DE⊥AB,∠C=90°,可知(
(2)由 AD=10,CD=8,得 AC=18.
在 Rt△ACB中, 得 AB=30.
由勾股定理得 BC=24.
所以在 Rt△DBC中,
18.解:在 Rt△ACE中,
在 Rt△BCD 中,∵∠ ︾105.7,
20.解:图略,由三视图可知这个礼品包装盒为正六棱柱,它的表面积为
