第二十八章 锐角三角函数 综合测试卷(含答案)
文档属性
| 名称 | 第二十八章 锐角三角函数 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 951.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 08:22:03 | ||
图片预览

文档简介
第二十八章 锐角三角函数 综合测试卷
(时间:100 分钟 满分:100 分)
题号 一 二 三 总分
得分
一、选择题(本大题共8 小题,每小题3分,共 24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在 Rt△ABC 中,各边都扩大为原来的4 倍,则锐角 A 的余弦值 ( )
A.扩大为原来的4倍 B.缩小为原来的
C.不变 D.无法确定
2.在△ABC中,若 则∠C的度数是 ( )
A.30° B.45° C.60° D.90°
3.在△ABC中,∠C=90°,如果 那么 sinB 的值为 ( )
C. D.
4.如图,在△ABC中,( 则 sinB 的值为 ( )
5.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆 AB 的长为( )
米 米 米 米
6.如图,在平面直角坐标系中,四边形 OABC 为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点 E 的坐标为 ( ) B.( ,2) C.( ,3)
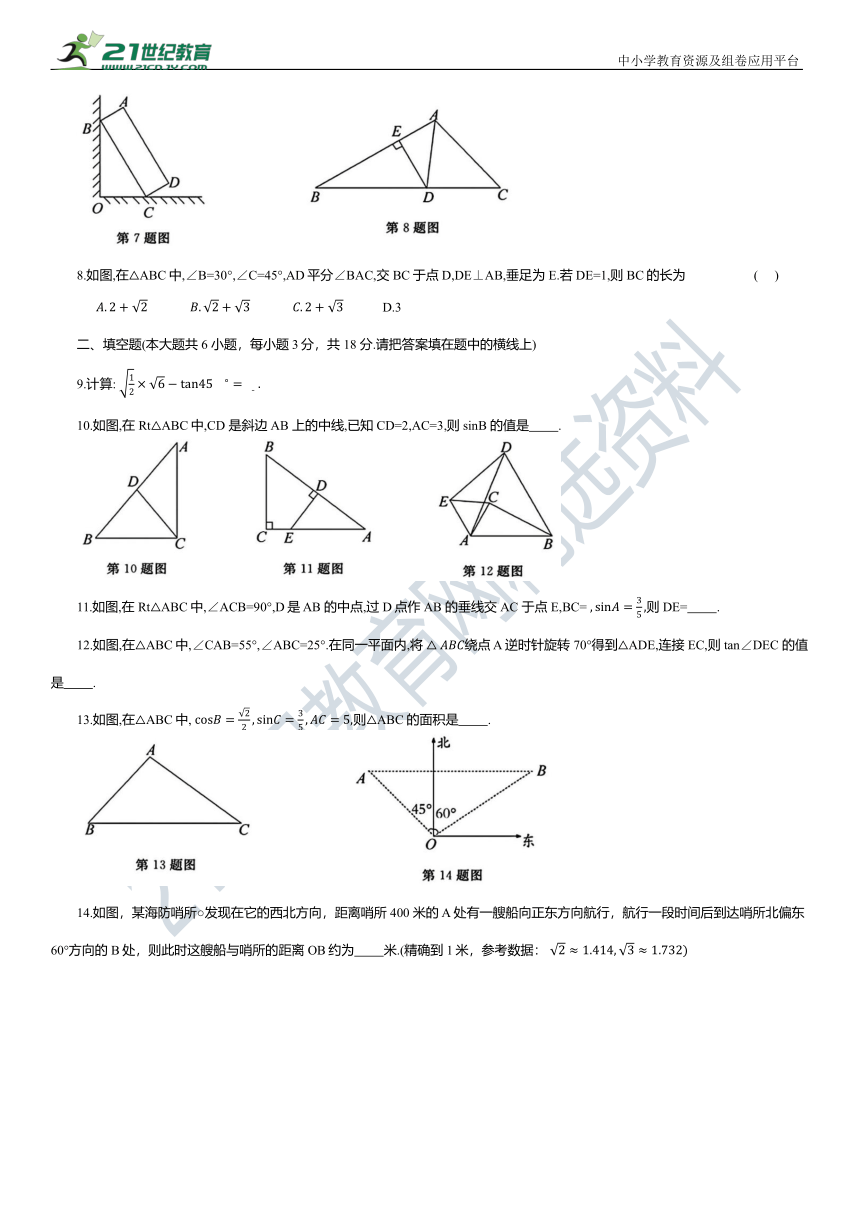
7.如图,一块矩形木板 ABCD斜靠在墙边(OC⊥OB,点 A,B,C,D,O在同一平面内).已知 AB=a,AD=b,∠BCO=x,则点 A 到 OC 的距离等于 ( )
A. asinx+bsinx B. acosx+bcosx C. asinx+bcosx D. acosx+bsinx
8.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC,交 BC于点D,DE⊥AB,垂足为 E.若 DE=1,则 BC的长为 ( )
D.3
二、填空题(本大题共6 小题,每小题3分,共 18 分.请把答案填在题中的横线上)
9.计算:
10.如图,在 Rt△ABC中,CD 是斜边AB 上的中线,已知 CD=2,AC=3,则sinB 的值是 .
11.如图,在 Rt△ABC中,∠ACB=90°,D是 AB 的中点,过 D点作AB 的垂线交AC 于点 E,BC= 则 DE= .
12.如图,在△ABC中,∠CAB=55°,∠ABC=25°.在同一平面内,将 绕点 A逆时针旋转 70°得到△ADE,连接 EC,则 tan∠DEC 的值是 .
13.如图,在△ABC中, 则△ABC的面积是 .
中小学教育资源及组卷应用平台
14.如图,某海防哨所○发现在它的西北方向,距离哨所 400 米的 A 处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东 60°方向的 B处,则此时这艘船与哨所的距离 OB约为 米.(精确到1米,参考数据:
三、解答题(本大题共 5小题,共 58分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分 12 分)计算
(1)
16.(本小题满分 12 分)
(1)在△ABC中,∠C=90°,AB=13,BC=5,求∠A 的正弦值、余弦值和正切值;
(2)在△ABC中, 求∠B, a,b.
17.(本小题满分 12分)
如图,在 中, 点 D、E 分别在 AC、AB上,BD 平分.
(1)求 DE、CD的长;
(2)求 的值.
18.(本小题满分 10 分)
数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像 DE 在高55 m的小山EC上,在A 处测得塑像底部E 的仰角为 ,再沿AC方向前进21 m到达 B 处,测得塑像顶部 D 的仰角为( ,求炎帝塑像 DE 的高度.(精确到 1m .参考数据:
19.(本小题满分 12 分)
图1 是一台实物投影仪,图 2 是它的示意图,折线. 表示固定支架,AO 垂直水平桌面OE 于点O,点 B 为旋转点,BC可转动,当 BC 绕点 B 顺时针旋转时,投影探头 CD始终垂直于水平桌面OE,经测量:A( cm.(结果精确到 0.1)
(1)如图 2,
①填空:
②求投影探头的端点 D 到桌面 OE 的距离.
(2)如图 3,将(1)中的 BC 向下旋转,当投影探头的端点 D 到桌面 OE 的距离为 6 cm 时,求 的大小.
(参考数据:si
一、1. C 2. D 3. B 4. D 5. B 6. D 7. D 8. A
二、9. -1 12.11 3. 14.566
三、15.(1)1
16.解:(1)∵∠C=90°,AB=13,BC=5,∴AC=√AB -BC = -5 =12,
17.(1)在 Rt△ADE中,由 得 AD=10,则
由 BD平分∠ABC,DE⊥AB,∠C=90°,可知(
(2)由 AD=10,CD=8,得 AC=18.
在 Rt△ACB中, 得 AB=30.
由勾股定理得 BC=24.
所以在 Rt△DBC中,
18.解:在 Rt△ACE中,
在 Rt△BCD 中,∵∠ ︾105.7,
19.解:图略,由三视图可知这个礼品包装盒为正六棱柱,它的表面积为
(时间:100 分钟 满分:100 分)
题号 一 二 三 总分
得分
一、选择题(本大题共8 小题,每小题3分,共 24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在 Rt△ABC 中,各边都扩大为原来的4 倍,则锐角 A 的余弦值 ( )
A.扩大为原来的4倍 B.缩小为原来的
C.不变 D.无法确定
2.在△ABC中,若 则∠C的度数是 ( )
A.30° B.45° C.60° D.90°
3.在△ABC中,∠C=90°,如果 那么 sinB 的值为 ( )
C. D.
4.如图,在△ABC中,( 则 sinB 的值为 ( )
5.某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆 AB 的长为( )
米 米 米 米
6.如图,在平面直角坐标系中,四边形 OABC 为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点 E 的坐标为 ( ) B.( ,2) C.( ,3)
7.如图,一块矩形木板 ABCD斜靠在墙边(OC⊥OB,点 A,B,C,D,O在同一平面内).已知 AB=a,AD=b,∠BCO=x,则点 A 到 OC 的距离等于 ( )
A. asinx+bsinx B. acosx+bcosx C. asinx+bcosx D. acosx+bsinx
8.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC,交 BC于点D,DE⊥AB,垂足为 E.若 DE=1,则 BC的长为 ( )
D.3
二、填空题(本大题共6 小题,每小题3分,共 18 分.请把答案填在题中的横线上)
9.计算:
10.如图,在 Rt△ABC中,CD 是斜边AB 上的中线,已知 CD=2,AC=3,则sinB 的值是 .
11.如图,在 Rt△ABC中,∠ACB=90°,D是 AB 的中点,过 D点作AB 的垂线交AC 于点 E,BC= 则 DE= .
12.如图,在△ABC中,∠CAB=55°,∠ABC=25°.在同一平面内,将 绕点 A逆时针旋转 70°得到△ADE,连接 EC,则 tan∠DEC 的值是 .
13.如图,在△ABC中, 则△ABC的面积是 .
中小学教育资源及组卷应用平台
14.如图,某海防哨所○发现在它的西北方向,距离哨所 400 米的 A 处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东 60°方向的 B处,则此时这艘船与哨所的距离 OB约为 米.(精确到1米,参考数据:
三、解答题(本大题共 5小题,共 58分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分 12 分)计算
(1)
16.(本小题满分 12 分)
(1)在△ABC中,∠C=90°,AB=13,BC=5,求∠A 的正弦值、余弦值和正切值;
(2)在△ABC中, 求∠B, a,b.
17.(本小题满分 12分)
如图,在 中, 点 D、E 分别在 AC、AB上,BD 平分.
(1)求 DE、CD的长;
(2)求 的值.
18.(本小题满分 10 分)
数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像 DE 在高55 m的小山EC上,在A 处测得塑像底部E 的仰角为 ,再沿AC方向前进21 m到达 B 处,测得塑像顶部 D 的仰角为( ,求炎帝塑像 DE 的高度.(精确到 1m .参考数据:
19.(本小题满分 12 分)
图1 是一台实物投影仪,图 2 是它的示意图,折线. 表示固定支架,AO 垂直水平桌面OE 于点O,点 B 为旋转点,BC可转动,当 BC 绕点 B 顺时针旋转时,投影探头 CD始终垂直于水平桌面OE,经测量:A( cm.(结果精确到 0.1)
(1)如图 2,
①填空:
②求投影探头的端点 D 到桌面 OE 的距离.
(2)如图 3,将(1)中的 BC 向下旋转,当投影探头的端点 D 到桌面 OE 的距离为 6 cm 时,求 的大小.
(参考数据:si
一、1. C 2. D 3. B 4. D 5. B 6. D 7. D 8. A
二、9. -1 12.11 3. 14.566
三、15.(1)1
16.解:(1)∵∠C=90°,AB=13,BC=5,∴AC=√AB -BC = -5 =12,
17.(1)在 Rt△ADE中,由 得 AD=10,则
由 BD平分∠ABC,DE⊥AB,∠C=90°,可知(
(2)由 AD=10,CD=8,得 AC=18.
在 Rt△ACB中, 得 AB=30.
由勾股定理得 BC=24.
所以在 Rt△DBC中,
18.解:在 Rt△ACE中,
在 Rt△BCD 中,∵∠ ︾105.7,
19.解:图略,由三视图可知这个礼品包装盒为正六棱柱,它的表面积为
