第二十九章 投影与视图 综合测试卷(含答案)
文档属性
| 名称 | 第二十九章 投影与视图 综合测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 13:18:58 | ||
图片预览

文档简介
第二十九章 投影与视图 综合测试卷
(时间:100 分钟 满分:100 分)
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,每小题3分,共 24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.列四个几何体中,主视图为圆的是 ( )
2.如图是由5 个相同的小正方体组成的几何体,该几何体的左视图是 ( )
3.如图,下列关于物体的主视图画法正确的是 ( )
4.如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是 ( )
5.某几何体的三视图如图所示,则下列说法错误的是 ( )
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是 1
D.该几何体的表面积为 18平方单位
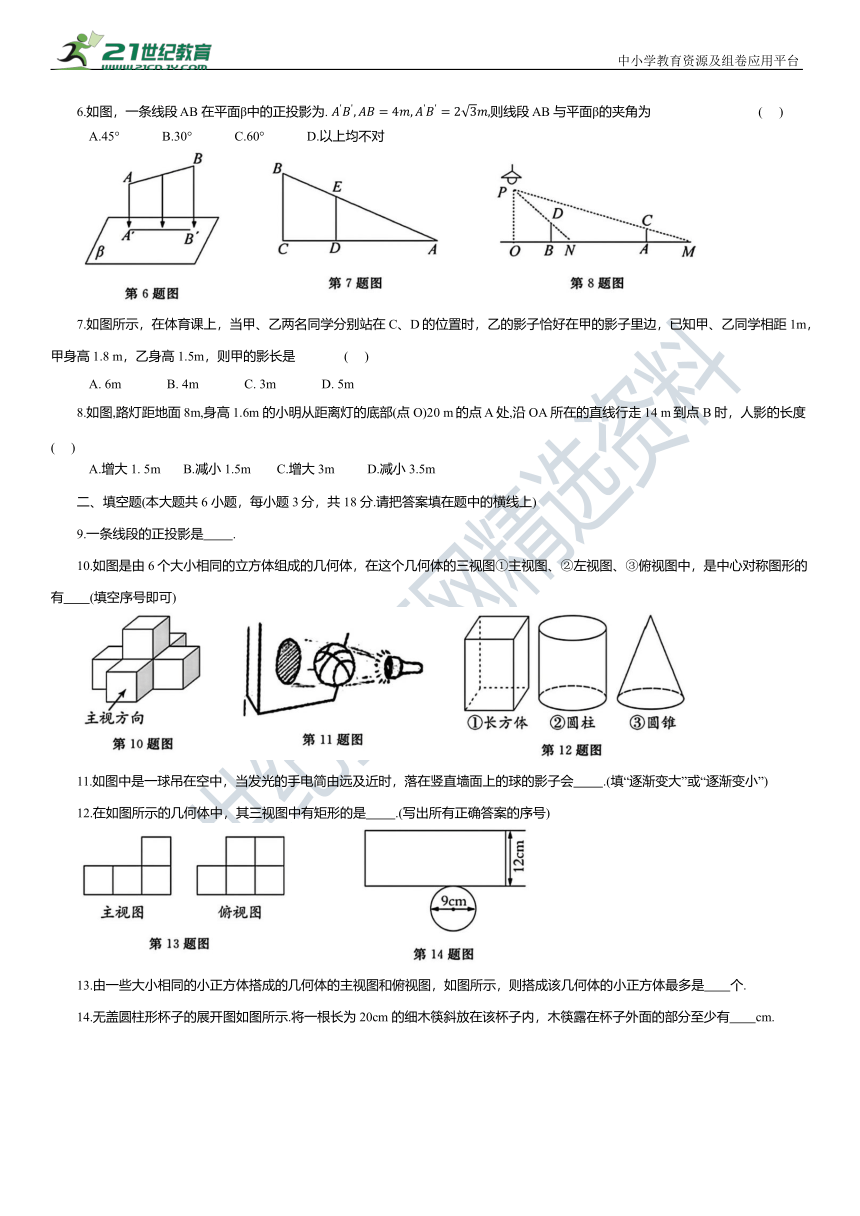
6.如图,一条线段 AB 在平面β中的正投影为. 则线段 AB 与平面β的夹角为 ( )
A.45° B.30° C.60° D.以上均不对
7.如图所示,在体育课上,当甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲、乙同学相距1m,甲身高 1.8 m,乙身高 1.5m,则甲的影长是 ( )
A. 6m B. 4m C. 3m D. 5m
8.如图,路灯距地面8m,身高1.6m 的小明从距离灯的底部(点 O)20 m的点 A 处,沿 OA 所在的直线行走 14 m到点 B 时,人影的长度 ( )
A.增大 1. 5m B.减小 1.5m C.增大 3m D.减小 3.5m
二、填空题(本大题共 6 小题,每小题3分,共 18 分.请把答案填在题中的横线上)
9.一条线段的正投影是 .
10.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图①主视图、②左视图、③俯视图中,是中心对称图形的有 (填空序号即可)
11.如图中是一球吊在空中,当发光的手电简由远及近时,落在竖直墙面上的球的影子会 .(填“逐渐变大”或“逐渐变小”)
12.在如图所示的几何体中,其三视图中有矩形的是 .(写出所有正确答案的序号)
13.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是 个.
中小学教育资源及组卷应用平台
14.无盖圆柱形杯子的展开图如图所示.将一根长为20cm 的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.
三、解答题(本大题共6 小题,共 58分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分8分)
5个棱长为 2 的正方体组成如图的几何体.
(1)该几何体的体积是 (立方单位),表面积是 (平方单位);
(2)画出该几何体的主视图、俯视图.
16.(本小题满分 10分)
如图,一张圆形桌面的直径. 高度为 1.8 m,桌面的上方有一盏电灯.
(1)请在图中画出灯泡发光时,桌面在地上的影子的最大宽度 EF;
(2)若 请求出灯泡离地面的高度.
17.(本小题满分 10 分)
如图分别是两根木棒及其影子的情形.
(1)哪个图反映了太阳光下的情形 哪个图反映了路灯下的情形
(2)在太阳光下,已知小明的身高是 1.8m,影长是 1.2m,旗杆的影长是 4m,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
18.(本小题满分 10分)
一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的名称,并根据图中所给的数据求出它的侧面积和体积.
19.(本小题满分 10分)
如图是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积.(全面积等于侧面积与两个底面积之和)
20.(本小题满分 10分)
如图是一个三棱柱,它的三视图如图所示,在 中, ,求AB 的长.
有一位同学认为 ,你认为他的想法正确吗
一、1. D 2. A 3. C 4. A 5. D 6. B 7. A 8. D
二、9.线段或点 10.③ 11.逐渐变大12.①② 13.7 14.5
三、15.(1)40 88(2)
主视图 俯视图
16.解:(1)如图所示:
(2)连接AB,过点O作OH⊥EF 于点 H,交 AB 于点 G.∵AB∥EF,∴△OAB∽△OEF.
即 解得 OG=1.2m.因此灯泡离地面的高度为OH=OG+GH=1.2+1.8=3(m)
17.解:(1)图②反映了太阳光下的情形,图①反映了路灯下的情形.
(2)设旗杆的高为 x m,根据题意,得 解得 x=6,所以旗杆的高为 6 m.
(3)图略.
18.解:该几何体是直四棱柱.由三视图知,棱柱底面的菱形的对角线长分别为 4 cm,3cm,高为 8cm ,则菱形的边长为 ,∴棱柱的侧面积为 ×8×4=80(cm ),棱柱的体积为
19.解:(1)这个多面体是正六棱柱;(2)侧面积为 6ab,全面积为
20.解:不正确.错误的原因是把钱线 EF 看成了线段 EF 的正投影.
正解:如图,过点 E 作 EH⊥FG于点 H,则 EF 的正投影是EH,EH=AB.在 Rt△EGH中,∠EGH=30°,EG=12 cm,所以 EH=6cm,即 AB=6 cm.
(时间:100 分钟 满分:100 分)
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,每小题3分,共 24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.列四个几何体中,主视图为圆的是 ( )
2.如图是由5 个相同的小正方体组成的几何体,该几何体的左视图是 ( )
3.如图,下列关于物体的主视图画法正确的是 ( )
4.如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是 ( )
5.某几何体的三视图如图所示,则下列说法错误的是 ( )
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是 1
D.该几何体的表面积为 18平方单位
6.如图,一条线段 AB 在平面β中的正投影为. 则线段 AB 与平面β的夹角为 ( )
A.45° B.30° C.60° D.以上均不对
7.如图所示,在体育课上,当甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲、乙同学相距1m,甲身高 1.8 m,乙身高 1.5m,则甲的影长是 ( )
A. 6m B. 4m C. 3m D. 5m
8.如图,路灯距地面8m,身高1.6m 的小明从距离灯的底部(点 O)20 m的点 A 处,沿 OA 所在的直线行走 14 m到点 B 时,人影的长度 ( )
A.增大 1. 5m B.减小 1.5m C.增大 3m D.减小 3.5m
二、填空题(本大题共 6 小题,每小题3分,共 18 分.请把答案填在题中的横线上)
9.一条线段的正投影是 .
10.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图①主视图、②左视图、③俯视图中,是中心对称图形的有 (填空序号即可)
11.如图中是一球吊在空中,当发光的手电简由远及近时,落在竖直墙面上的球的影子会 .(填“逐渐变大”或“逐渐变小”)
12.在如图所示的几何体中,其三视图中有矩形的是 .(写出所有正确答案的序号)
13.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是 个.
中小学教育资源及组卷应用平台
14.无盖圆柱形杯子的展开图如图所示.将一根长为20cm 的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.
三、解答题(本大题共6 小题,共 58分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分8分)
5个棱长为 2 的正方体组成如图的几何体.
(1)该几何体的体积是 (立方单位),表面积是 (平方单位);
(2)画出该几何体的主视图、俯视图.
16.(本小题满分 10分)
如图,一张圆形桌面的直径. 高度为 1.8 m,桌面的上方有一盏电灯.
(1)请在图中画出灯泡发光时,桌面在地上的影子的最大宽度 EF;
(2)若 请求出灯泡离地面的高度.
17.(本小题满分 10 分)
如图分别是两根木棒及其影子的情形.
(1)哪个图反映了太阳光下的情形 哪个图反映了路灯下的情形
(2)在太阳光下,已知小明的身高是 1.8m,影长是 1.2m,旗杆的影长是 4m,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
18.(本小题满分 10分)
一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的名称,并根据图中所给的数据求出它的侧面积和体积.
19.(本小题满分 10分)
如图是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积.(全面积等于侧面积与两个底面积之和)
20.(本小题满分 10分)
如图是一个三棱柱,它的三视图如图所示,在 中, ,求AB 的长.
有一位同学认为 ,你认为他的想法正确吗
一、1. D 2. A 3. C 4. A 5. D 6. B 7. A 8. D
二、9.线段或点 10.③ 11.逐渐变大12.①② 13.7 14.5
三、15.(1)40 88(2)
主视图 俯视图
16.解:(1)如图所示:
(2)连接AB,过点O作OH⊥EF 于点 H,交 AB 于点 G.∵AB∥EF,∴△OAB∽△OEF.
即 解得 OG=1.2m.因此灯泡离地面的高度为OH=OG+GH=1.2+1.8=3(m)
17.解:(1)图②反映了太阳光下的情形,图①反映了路灯下的情形.
(2)设旗杆的高为 x m,根据题意,得 解得 x=6,所以旗杆的高为 6 m.
(3)图略.
18.解:该几何体是直四棱柱.由三视图知,棱柱底面的菱形的对角线长分别为 4 cm,3cm,高为 8cm ,则菱形的边长为 ,∴棱柱的侧面积为 ×8×4=80(cm ),棱柱的体积为
19.解:(1)这个多面体是正六棱柱;(2)侧面积为 6ab,全面积为
20.解:不正确.错误的原因是把钱线 EF 看成了线段 EF 的正投影.
正解:如图,过点 E 作 EH⊥FG于点 H,则 EF 的正投影是EH,EH=AB.在 Rt△EGH中,∠EGH=30°,EG=12 cm,所以 EH=6cm,即 AB=6 cm.
