九年级下册《第三章圆》复习与检测试卷(含解析)
文档属性
| 名称 | 九年级下册《第三章圆》复习与检测试卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级下册《第三章圆》复习与检测试卷
选择题(本大题共有40个小题,每小题4分,共40分)
1.如图,∠AOB是⊙0的圆心角,∠AOB=80°则弧AB所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°
2.如图,已知⊙O弦AB的长6cm,OC⊥AB,OC=4cm,则⊙O的半径为( )
A.6cm B.5cm C.4cm D.3cm
3.如图,若是的直径,是的弦,,则的度数为( )
A. B. C. D.
4.如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
A.相等 B.互余 C.互补 D.无法确定
【答案】A
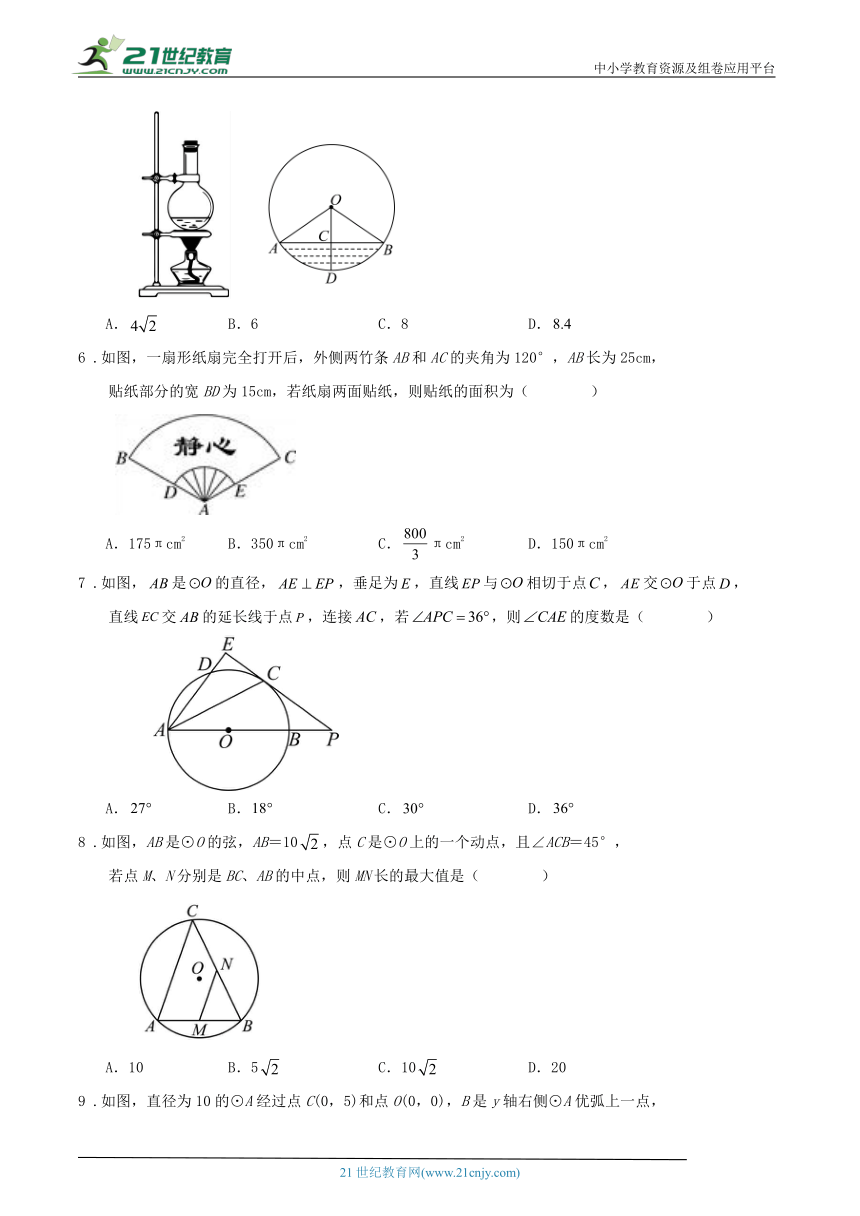
5 .如图,一个底部呈球形的烧瓶,球的半径为,瓶内液体的最大深度.
则截面圆中弦的长为( )
A. B.6 C.8 D.
6 .如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,
贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
A.175πcm2 B.350πcm2 C.πcm2 D.150πcm2
7 .如图,是的直径,,垂足为,直线与相切于点,交于点,
直线交的延长线于点,连接,若,则的度数是( )
A. B. C. D.
8 .如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,
若点M、N分别是BC、AB的中点,则MN长的最大值是( )
A.10 B.5 C.10 D.20
9 .如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,
则∠OBC的余弦值为( )
A. B. C. D.
10 .图是型号为24英寸(车轮的直径为24英寸,约)的自行车,
现要在自行车两轮的阴影部分(分别以,为圆心的两个扇形)装上挡水的铁皮,
量出四边形中,,那么安装单侧(阴影部分)
需要的铁皮面积约是( )
A. B. C. D.
填空题(本大题共有6个小题,每小题4分,共24分)
11.在直径为1000mm的圆柱形油槽内装入一些油后,截面如图所示,
若油面宽AB=800mm,则油的最大深度为 mm.
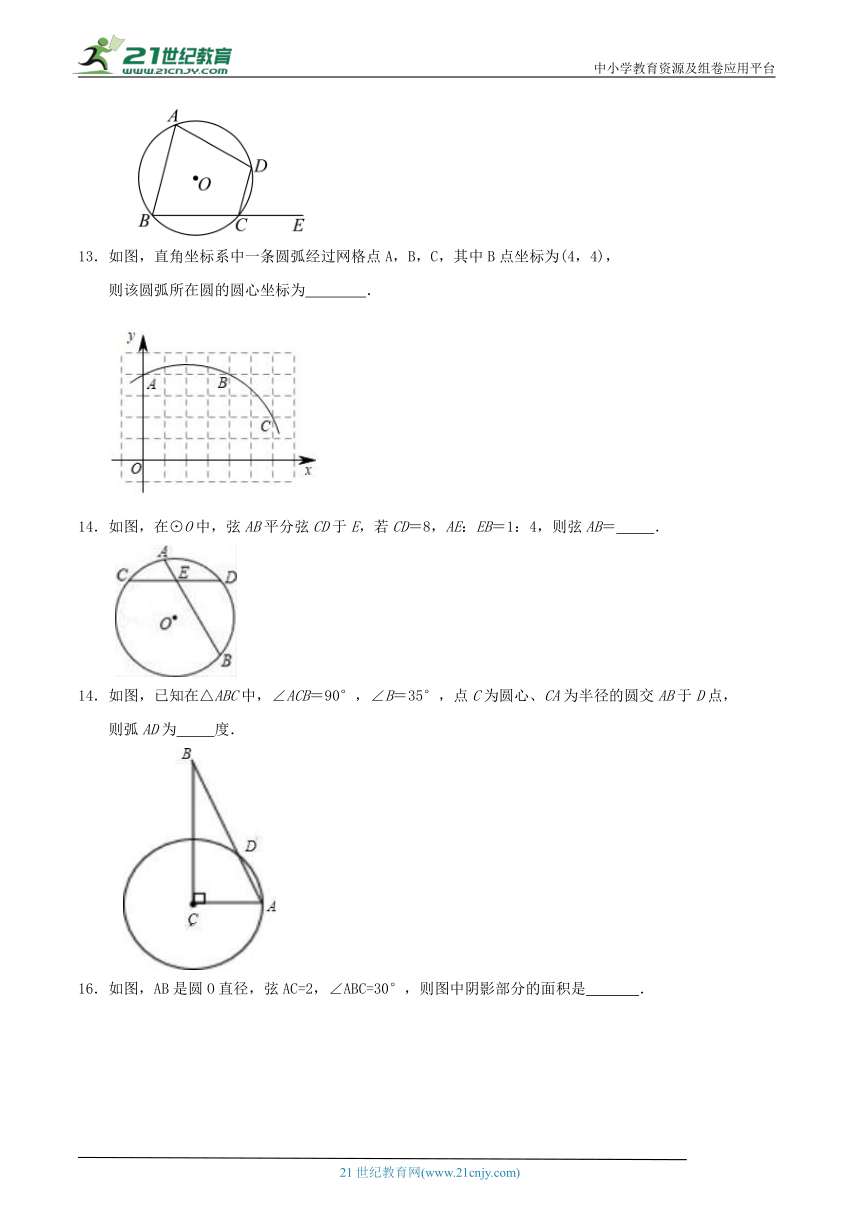
12 .如图,四边形内接于,若,则四边形的外角的度数为________
如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),
则该圆弧所在圆的圆心坐标为 .
14.如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB= .
如图,已知在△ABC中,∠ACB=90°,∠B=35°,点C为圆心、CA为半径的圆交AB于D点,
则弧AD为 度.
16.如图,AB是圆O直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是 .
三、解答题(本大题共有6个小题,共36分)
17.如图,在半径为13的⊙O中,OC垂直弦AB于点D,交⊙O于点C,AB=24,求CD的长 .
18.如图,在⊙O中,直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30 cm.求直径AB的长.
如图,已知点E在直角△ABC的斜边AB上,
以AE为直径的⊙O与直角边BC相交于点D,AD平分∠BAC.
(1)求证,BC是⊙O的切线.
(2)若BE=2,BD=4,求⊙O的半径.
如图,在△ABC中,∠C=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,
与边BC交于点F,过点E作EH⊥AB于点H,连接BE
(1)求证:EH=EC;
(2)若AB=4,sinA=,求AD的长.
21.如图,为的直径,C为上的中点,于的延长线交于点E.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
22 .如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,
过点P作PD⊥OP交⊙O于点D.
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当弧DC=弧AC时,延长AB至点E,使BE=AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
九年级下册《第三章圆》复习与检测试卷 解析
选择题(本大题共有40个小题,每小题4分,共40分)
1.如图,∠AOB是⊙0的圆心角,∠AOB=80°则弧AB所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°
【答案】A
【详解】解:∵∠ACB与∠AOB同对着弧AB ,
而∠ACB为圆周角,∠AOB为圆心角;
∴∠ACB=°
故选A.
2.如图,已知⊙O弦AB的长6cm,OC⊥AB,OC=4cm,则⊙O的半径为( )
A.6cm B.5cm C.4cm D.3cm
【答案】B
【详解】试题分析:连接OA构建Rt△AOC,然后在Rt△AOC中利用勾股定理求⊙O的半径OA的长即可.
解:连接OA.
∵OC⊥AB,AB=6cm,
∴AC=BC=AB=3cm(垂径定理);
在Rt△AOC中,根据勾股定理知,
AO2=OC2+AC2,
∴OA2=16+9=25,
∴OA=5cm;
故选B.
3.如图,若是的直径,是的弦,,则的度数为( )
A. B. C. D.
【答案】D
【分析】由AB是⊙O的直径,推出∠ADB=90°,再由∠ABD=58°,求出∠A=32°,
根据圆周角定理推出∠C=32°.
【详解】解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABD=58°,
∴∠A=32°,
∴∠C=32°.
故选:D.
4.如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
A.相等 B.互余 C.互补 D.无法确定
【答案】A
【分析】根据圆内接四边形的性质和邻补角的概念解答即可.
【详解】∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠DCB=180°,
∵∠DCE+∠DCB=180°,
∴∠DAB=∠DCE,
故选A.
5 .如图,一个底部呈球形的烧瓶,球的半径为,瓶内液体的最大深度.
则截面圆中弦的长为( )
A. B.6 C.8 D.
【答案】B
【分析】由垂径定理和勾股定理分别求出的长,即可得出答案.
【详解】解:如图所示,
由题意得:,,
,
∵,
∴,
在中,根据勾股定理得,
,
∴,
即截面圆中弦的长为,
故选:B.
6 .如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,
贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
A.175πcm2 B.350πcm2 C.πcm2 D.150πcm2
【答案】B
【分析】贴纸部分的面积等于大扇形的面积减去小扇形ADE的面积,由此即可解答.
【详解】∵AB=25,BD=15,
∴AD=10,
∴S贴纸= =175π×2=350cm2,
故选B.
7 .如图,是的直径,,垂足为,直线与相切于点,交于点,
直线交的延长线于点,连接,若,则的度数是( )
A. B. C. D.
【答案】A
【分析】根据垂直的定义及平行线的判定可知,
再利用等腰三角形的性质及平行线的性质即可解答.
【详解】解:连接,
∵与相切于,
∴半径,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
故选:.
8 .如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,
若点M、N分别是BC、AB的中点,则MN长的最大值是( )
A.10 B.5 C.10 D.20
【答案】A
【分析】连接OA、OB,如图,根据圆周角定理得到∠AOB=2∠ACB=90°,则OA=AB=10,
再根据三角形中位线性质得到MN=AC,然后利用AC为直径时,AC的值最大可确定MN的最大值.
【详解】连接OA、OB,
∴∠AOB=2∠ACB=2×45°=90°,
∴△OAB为等腰直角三角形,
∴OA=AB=×10=10,
∵点M、N分别是AB、BC的中点,
∴MN=AC,
当AC为直径时,AC的值最大,
∴MN的最大值为10.
故选A.
9 .如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,
则∠OBC的余弦值为( )
A. B. C. D.
【答案】C
【分析】连接CD,由直径所对的圆周角是直角,可得CD是直径;
由同弧所对的圆周角相等可得∠OBC=∠ODC,在Rt△OCD中,由OC和CD的长可求出sin∠ODC.
【详解】设⊙A交x轴于另一点D,连接CD,
∵∠COD=90°,
∴CD为直径,
∵直径为10,
∴CD=10,
∵点C(0,5)和点O(0,0),
∴OC=5,
∴sin∠ODC= = ,
∴∠ODC=30°,
∴∠OBC=∠ODC=30°,
∴cos∠OBC=cos30°= .
故选C.
10 .图是型号为24英寸(车轮的直径为24英寸,约)的自行车,
现要在自行车两轮的阴影部分(分别以,为圆心的两个扇形)装上挡水的铁皮,
量出四边形中,,那么安装单侧(阴影部分)需要的铁皮面积约是( )
A. B. C. D.
【答案】A
【分析】求出圆心角,再运用扇形的面积公式计算即可.
【详解】∵四边形中,,,
∴,
∵车轮的直径为24英寸,约,
∴需要的铁皮面积约是,
故选A.
填空题(本大题共有6个小题,每小题4分,共24分)
11.在直径为1000mm的圆柱形油槽内装入一些油后,截面如图所示,
若油面宽AB=800mm,则油的最大深度为 mm.
【答案】200
【详解】试题解析:过点O作OM⊥AB交AB于M,交弧AB于点E. 连接OA.
在Rt△OAM中:OA=500mm,
根据勾股定理可得OM=300mm,则油的最大深度ME为200mm.
故答案为200.
12 .如图,四边形内接于,若,则四边形的外角的度数为________
【答案】
【分析】此题考查了圆内接四边形的性质,根据圆的内接四边形的性质,
可得,即可求解.
【详解】解:四边形内接于,
,
,
,
,
.
故选:A.
13 .如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),
则该圆弧所在圆的圆心坐标为 .
【答案】(2,0)
【详解】解:根据垂径定理的推论:弦的垂直平分线必过圆心,
所以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,
则圆心是(2,0),
故答案为:(2,0).
14.如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB= .
【答案】10
【分析】设AE=x,则EB=4x,由弦AB平分弦CD于E,得到CE=DE=CD=4,
再根据相交弦定理得x 4x=4 4,解得x=2或x=-2(舍去),然后计算5x即可.
【详解】解:设AE=x,则EB=4x,
∵弦AB平分弦CD于E,
∴CE=DE=CD=×8=4,
∵AE BE=CE DE,
即x 4x=4 4,解得x=2或x=﹣2(舍去),
∴AB=AE+BE=5x=10.
故答案为:10.
如图,已知在△ABC中,∠ACB=90°,∠B=35°,点C为圆心、CA为半径的圆交AB于D点,
则弧AD为 度.
【答案】70
【分析】根据已知和三角形内角和定理即可求得∠ACD的度数,即得到了弧AD的度数.
【详解】解:连接CD,
∵∠ACB=90°,∠B=35°
∴∠A=90°-∠B=55°
∵CA=CD
∴∠A=∠CDA=55°
∴∠ACD=180°-2∠A=70°
∴弧AD的度数是70°
16.如图,AB是圆O直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是 .
【答案】
【详解】试题分析:如图,连接OC,则图中阴影部分的面积=扇形OBC的面积-△ABC的面积.
∵AB是直径,∴∠ACB=90°.
∵∠ABC=30°,∴∠BAC=60°.∴∠BOC=120°.
∴在Rt△ABC中,AC=2,∠ABC=30°,∴AB=2AC=4,BC=.
∵OC是△ABC斜边上的中线,
∴.
∴.
三、解答题(本大题共有6个小题,共36分)
17.如图,在半径为13的⊙O中,OC垂直弦AB于点D,交⊙O于点C,AB=24,求CD的长 .
【答案】
【分析】连接OA,根据垂径定理求出AD=12,根据勾股定理求出OD,即可得出答案.
【详解】试题解析:
连接OA,
∵AB⊥CO,OC过O,
∴AD=BDAB=12,
在Rt△OAD中,∠ODA=90°,OA=13,AD=12,由勾股定理得:OD=5,
∴CD=13﹣5=8.
18.如图,在⊙O中,直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30 cm.求直径AB的长.
【答案】AB=30 cm.
【分析】连接OC,根据等边对等角以及三角形的外角的性质,
即可求得∠COD的度数,OC是半径,则长度可以求得:在直角△OCD中,
利用在直角三角形中,30°角所对的直角边等于斜边的一半可求出OC,进而求出AB的长.
【详解】连接OC.
∵OA=OC,∠A=30°,∴∠A=∠ACO=30°,∴∠COD=∠A+∠ACO=60°.
∵DC切⊙O于C,∴∠OCD=90°,∴∠D=30°.
∵OD=30 cm,∴OC=OD=15 cm,∴AB=2OC=30cm.
19 .如图,已知点E在直角△ABC的斜边AB上,
以AE为直径的⊙O与直角边BC相交于点D,AD平分∠BAC.
(1)求证,BC是⊙O的切线.
(2)若BE=2,BD=4,求⊙O的半径.
【答案】(1)证明见解析;(2)3
【分析】(1)先连接OD,再由OD∥AC和AC⊥BC可知OD⊥BC从而得证;
(2)利用切割线定理可先求出AB,进而求出圆的直径,半径则可求出.
【详解】(1)证明:连接OD,
∵AD平分∠BAC
∴∠1=∠2
∵OA=OD
∴∠1=∠3
∴∠2=∠3;
∴OD∥AC,
又∵AC⊥BC,
∴OD⊥BC,
∴BC是⊙O的切线,
(2)解:∵BC与圆相切于点D.
∴BD2=BE BA,
∵BE=2,BD=4,
∴BA=8,
∴AE=AB﹣BE=6,
∴⊙O的半径为3.
20 .如图,在△ABC中,∠C=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,
与边BC交于点F,过点E作EH⊥AB于点H,连接BE
(1)求证:EH=EC;
(2)若AB=4,sinA=,求AD的长.
【答案】(1)证明见解析(2)
【分析】(1)连接OE,易证OE∥BC,继而结合已知证明∠CBE=∠EBO,
然后利用角平分线的性质即可证得EH=EC;
由sinA==,设OE=2a,AO=3a(a≠0),根据AB的长可求得a的值,
再根据AD=AB-BD即可求得答案.
【详解】(1)如图,连接OE,
∵AC与⊙O相切,
∴OE⊥AC,且BC⊥AC,
∴OE∥BC
∴∠CBE=∠OEB,
∵EO=OB,
∴∠EBO=∠OEB
∴∠CBE=∠EBO,且CE⊥BC,EH⊥AB,
∴CE=EH
(2)∵sinA==,
∴设OE=2a,AO=3a,(a≠0)
∴OB=OE=2a,
∵AB=AO+OB=3a+2a=4
∴a=,
∵AD=AB﹣BD=4﹣4a
∴AD=.
21.如图,为的直径,C为上的中点,于的延长线交于点E.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
【答案】(1)见解析
(2).
【分析】本题考查了切线的判定以及圆周角定理和扇形的面积公式.
连接,利用半径相等、圆周角定理求得,推出,
从而得到,即可证明是的切线;
设半径为r,利用勾股定理得到,解得,
再计算出,然后根据扇形的面积公式,利用进行计算即可.
【详解】(1)证明:连接,如图,
∵,
∴,
∵C为上的中点,即,
∴,
∴,
∴,
∵,
∴,
∵点C在上,
∴是的切线;
(2)解:连接,设半径为r,
在中,∵,
∴,
解得,
∴,
则,即点B是斜边的中点,
∴,
∴,
∴是等边三角形,
∴,
∴.
22 .如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,
过点P作PD⊥OP交⊙O于点D.
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当弧DC=弧AC时,延长AB至点E,使BE=AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
【答案】(1)2;(2)①证明见解析;②3﹣3.
【分析】(1)根据题意首先得出半径长,再利用锐角三角三角函数关系得出OP,PD的长;
(2)①首先得出△OBD是等边三角形,进而得出∠ODE=∠OFB=90°,求出答案即可;
②首先求出CF的长,进而利用直角三角形的性质得出PF的长,进而得出答案.
【详解】解:(1)如图2,连接OD,
∵OP⊥PD,PD//AB,
∴∠POB=90°,
∵⊙O的直径AB=12,
∴OB=OD=6,
在Rt△POB中,∠ABC=30°,
∴OP=OB tan30°=6×=2,
在Rt△POD中,
PD=;
(2)①如图3,连接OD,交CB于点F,连接BD,
∵,
∴∠DBC=∠ABC=30°,
∴∠ABD=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴OD⊥FB,OB=BD, ∠OBD=∠ODB=60°,
∵BE=AB,
∴OB=BE,
∴BD=BE,
∴∠E=∠BDE=∠OBD=30°,
∴∠E=∠ABC,
∴BF//ED,
∴∠ODE=∠OFB=90°,
∴DE是⊙O的切线;
②由①知,OD⊥BC,
∴CF=FB=OB cos30°=6×=3,
在Rt△POD中,OF=DF,
∴PF=DO=3(直角三角形斜边上的中线,等于斜边的一半),
∴CP=CF﹣PF=3﹣3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级下册《第三章圆》复习与检测试卷
选择题(本大题共有40个小题,每小题4分,共40分)
1.如图,∠AOB是⊙0的圆心角,∠AOB=80°则弧AB所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°
2.如图,已知⊙O弦AB的长6cm,OC⊥AB,OC=4cm,则⊙O的半径为( )
A.6cm B.5cm C.4cm D.3cm
3.如图,若是的直径,是的弦,,则的度数为( )
A. B. C. D.
4.如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
A.相等 B.互余 C.互补 D.无法确定
【答案】A
5 .如图,一个底部呈球形的烧瓶,球的半径为,瓶内液体的最大深度.
则截面圆中弦的长为( )
A. B.6 C.8 D.
6 .如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,
贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
A.175πcm2 B.350πcm2 C.πcm2 D.150πcm2
7 .如图,是的直径,,垂足为,直线与相切于点,交于点,
直线交的延长线于点,连接,若,则的度数是( )
A. B. C. D.
8 .如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,
若点M、N分别是BC、AB的中点,则MN长的最大值是( )
A.10 B.5 C.10 D.20
9 .如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,
则∠OBC的余弦值为( )
A. B. C. D.
10 .图是型号为24英寸(车轮的直径为24英寸,约)的自行车,
现要在自行车两轮的阴影部分(分别以,为圆心的两个扇形)装上挡水的铁皮,
量出四边形中,,那么安装单侧(阴影部分)
需要的铁皮面积约是( )
A. B. C. D.
填空题(本大题共有6个小题,每小题4分,共24分)
11.在直径为1000mm的圆柱形油槽内装入一些油后,截面如图所示,
若油面宽AB=800mm,则油的最大深度为 mm.
12 .如图,四边形内接于,若,则四边形的外角的度数为________
如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),
则该圆弧所在圆的圆心坐标为 .
14.如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB= .
如图,已知在△ABC中,∠ACB=90°,∠B=35°,点C为圆心、CA为半径的圆交AB于D点,
则弧AD为 度.
16.如图,AB是圆O直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是 .
三、解答题(本大题共有6个小题,共36分)
17.如图,在半径为13的⊙O中,OC垂直弦AB于点D,交⊙O于点C,AB=24,求CD的长 .
18.如图,在⊙O中,直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30 cm.求直径AB的长.
如图,已知点E在直角△ABC的斜边AB上,
以AE为直径的⊙O与直角边BC相交于点D,AD平分∠BAC.
(1)求证,BC是⊙O的切线.
(2)若BE=2,BD=4,求⊙O的半径.
如图,在△ABC中,∠C=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,
与边BC交于点F,过点E作EH⊥AB于点H,连接BE
(1)求证:EH=EC;
(2)若AB=4,sinA=,求AD的长.
21.如图,为的直径,C为上的中点,于的延长线交于点E.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
22 .如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,
过点P作PD⊥OP交⊙O于点D.
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当弧DC=弧AC时,延长AB至点E,使BE=AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
九年级下册《第三章圆》复习与检测试卷 解析
选择题(本大题共有40个小题,每小题4分,共40分)
1.如图,∠AOB是⊙0的圆心角,∠AOB=80°则弧AB所对圆周角∠ACB的度数是( )
A.40° B.45° C.50° D.80°
【答案】A
【详解】解:∵∠ACB与∠AOB同对着弧AB ,
而∠ACB为圆周角,∠AOB为圆心角;
∴∠ACB=°
故选A.
2.如图,已知⊙O弦AB的长6cm,OC⊥AB,OC=4cm,则⊙O的半径为( )
A.6cm B.5cm C.4cm D.3cm
【答案】B
【详解】试题分析:连接OA构建Rt△AOC,然后在Rt△AOC中利用勾股定理求⊙O的半径OA的长即可.
解:连接OA.
∵OC⊥AB,AB=6cm,
∴AC=BC=AB=3cm(垂径定理);
在Rt△AOC中,根据勾股定理知,
AO2=OC2+AC2,
∴OA2=16+9=25,
∴OA=5cm;
故选B.
3.如图,若是的直径,是的弦,,则的度数为( )
A. B. C. D.
【答案】D
【分析】由AB是⊙O的直径,推出∠ADB=90°,再由∠ABD=58°,求出∠A=32°,
根据圆周角定理推出∠C=32°.
【详解】解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABD=58°,
∴∠A=32°,
∴∠C=32°.
故选:D.
4.如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
A.相等 B.互余 C.互补 D.无法确定
【答案】A
【分析】根据圆内接四边形的性质和邻补角的概念解答即可.
【详解】∵四边形ABCD是⊙O的内接四边形,
∴∠DAB+∠DCB=180°,
∵∠DCE+∠DCB=180°,
∴∠DAB=∠DCE,
故选A.
5 .如图,一个底部呈球形的烧瓶,球的半径为,瓶内液体的最大深度.
则截面圆中弦的长为( )
A. B.6 C.8 D.
【答案】B
【分析】由垂径定理和勾股定理分别求出的长,即可得出答案.
【详解】解:如图所示,
由题意得:,,
,
∵,
∴,
在中,根据勾股定理得,
,
∴,
即截面圆中弦的长为,
故选:B.
6 .如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,
贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
A.175πcm2 B.350πcm2 C.πcm2 D.150πcm2
【答案】B
【分析】贴纸部分的面积等于大扇形的面积减去小扇形ADE的面积,由此即可解答.
【详解】∵AB=25,BD=15,
∴AD=10,
∴S贴纸= =175π×2=350cm2,
故选B.
7 .如图,是的直径,,垂足为,直线与相切于点,交于点,
直线交的延长线于点,连接,若,则的度数是( )
A. B. C. D.
【答案】A
【分析】根据垂直的定义及平行线的判定可知,
再利用等腰三角形的性质及平行线的性质即可解答.
【详解】解:连接,
∵与相切于,
∴半径,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴.
故选:.
8 .如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,
若点M、N分别是BC、AB的中点,则MN长的最大值是( )
A.10 B.5 C.10 D.20
【答案】A
【分析】连接OA、OB,如图,根据圆周角定理得到∠AOB=2∠ACB=90°,则OA=AB=10,
再根据三角形中位线性质得到MN=AC,然后利用AC为直径时,AC的值最大可确定MN的最大值.
【详解】连接OA、OB,
∴∠AOB=2∠ACB=2×45°=90°,
∴△OAB为等腰直角三角形,
∴OA=AB=×10=10,
∵点M、N分别是AB、BC的中点,
∴MN=AC,
当AC为直径时,AC的值最大,
∴MN的最大值为10.
故选A.
9 .如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,
则∠OBC的余弦值为( )
A. B. C. D.
【答案】C
【分析】连接CD,由直径所对的圆周角是直角,可得CD是直径;
由同弧所对的圆周角相等可得∠OBC=∠ODC,在Rt△OCD中,由OC和CD的长可求出sin∠ODC.
【详解】设⊙A交x轴于另一点D,连接CD,
∵∠COD=90°,
∴CD为直径,
∵直径为10,
∴CD=10,
∵点C(0,5)和点O(0,0),
∴OC=5,
∴sin∠ODC= = ,
∴∠ODC=30°,
∴∠OBC=∠ODC=30°,
∴cos∠OBC=cos30°= .
故选C.
10 .图是型号为24英寸(车轮的直径为24英寸,约)的自行车,
现要在自行车两轮的阴影部分(分别以,为圆心的两个扇形)装上挡水的铁皮,
量出四边形中,,那么安装单侧(阴影部分)需要的铁皮面积约是( )
A. B. C. D.
【答案】A
【分析】求出圆心角,再运用扇形的面积公式计算即可.
【详解】∵四边形中,,,
∴,
∵车轮的直径为24英寸,约,
∴需要的铁皮面积约是,
故选A.
填空题(本大题共有6个小题,每小题4分,共24分)
11.在直径为1000mm的圆柱形油槽内装入一些油后,截面如图所示,
若油面宽AB=800mm,则油的最大深度为 mm.
【答案】200
【详解】试题解析:过点O作OM⊥AB交AB于M,交弧AB于点E. 连接OA.
在Rt△OAM中:OA=500mm,
根据勾股定理可得OM=300mm,则油的最大深度ME为200mm.
故答案为200.
12 .如图,四边形内接于,若,则四边形的外角的度数为________
【答案】
【分析】此题考查了圆内接四边形的性质,根据圆的内接四边形的性质,
可得,即可求解.
【详解】解:四边形内接于,
,
,
,
,
.
故选:A.
13 .如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),
则该圆弧所在圆的圆心坐标为 .
【答案】(2,0)
【详解】解:根据垂径定理的推论:弦的垂直平分线必过圆心,
所以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,
则圆心是(2,0),
故答案为:(2,0).
14.如图,在⊙O中,弦AB平分弦CD于E,若CD=8,AE:EB=1:4,则弦AB= .
【答案】10
【分析】设AE=x,则EB=4x,由弦AB平分弦CD于E,得到CE=DE=CD=4,
再根据相交弦定理得x 4x=4 4,解得x=2或x=-2(舍去),然后计算5x即可.
【详解】解:设AE=x,则EB=4x,
∵弦AB平分弦CD于E,
∴CE=DE=CD=×8=4,
∵AE BE=CE DE,
即x 4x=4 4,解得x=2或x=﹣2(舍去),
∴AB=AE+BE=5x=10.
故答案为:10.
如图,已知在△ABC中,∠ACB=90°,∠B=35°,点C为圆心、CA为半径的圆交AB于D点,
则弧AD为 度.
【答案】70
【分析】根据已知和三角形内角和定理即可求得∠ACD的度数,即得到了弧AD的度数.
【详解】解:连接CD,
∵∠ACB=90°,∠B=35°
∴∠A=90°-∠B=55°
∵CA=CD
∴∠A=∠CDA=55°
∴∠ACD=180°-2∠A=70°
∴弧AD的度数是70°
16.如图,AB是圆O直径,弦AC=2,∠ABC=30°,则图中阴影部分的面积是 .
【答案】
【详解】试题分析:如图,连接OC,则图中阴影部分的面积=扇形OBC的面积-△ABC的面积.
∵AB是直径,∴∠ACB=90°.
∵∠ABC=30°,∴∠BAC=60°.∴∠BOC=120°.
∴在Rt△ABC中,AC=2,∠ABC=30°,∴AB=2AC=4,BC=.
∵OC是△ABC斜边上的中线,
∴.
∴.
三、解答题(本大题共有6个小题,共36分)
17.如图,在半径为13的⊙O中,OC垂直弦AB于点D,交⊙O于点C,AB=24,求CD的长 .
【答案】
【分析】连接OA,根据垂径定理求出AD=12,根据勾股定理求出OD,即可得出答案.
【详解】试题解析:
连接OA,
∵AB⊥CO,OC过O,
∴AD=BDAB=12,
在Rt△OAD中,∠ODA=90°,OA=13,AD=12,由勾股定理得:OD=5,
∴CD=13﹣5=8.
18.如图,在⊙O中,直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30 cm.求直径AB的长.
【答案】AB=30 cm.
【分析】连接OC,根据等边对等角以及三角形的外角的性质,
即可求得∠COD的度数,OC是半径,则长度可以求得:在直角△OCD中,
利用在直角三角形中,30°角所对的直角边等于斜边的一半可求出OC,进而求出AB的长.
【详解】连接OC.
∵OA=OC,∠A=30°,∴∠A=∠ACO=30°,∴∠COD=∠A+∠ACO=60°.
∵DC切⊙O于C,∴∠OCD=90°,∴∠D=30°.
∵OD=30 cm,∴OC=OD=15 cm,∴AB=2OC=30cm.
19 .如图,已知点E在直角△ABC的斜边AB上,
以AE为直径的⊙O与直角边BC相交于点D,AD平分∠BAC.
(1)求证,BC是⊙O的切线.
(2)若BE=2,BD=4,求⊙O的半径.
【答案】(1)证明见解析;(2)3
【分析】(1)先连接OD,再由OD∥AC和AC⊥BC可知OD⊥BC从而得证;
(2)利用切割线定理可先求出AB,进而求出圆的直径,半径则可求出.
【详解】(1)证明:连接OD,
∵AD平分∠BAC
∴∠1=∠2
∵OA=OD
∴∠1=∠3
∴∠2=∠3;
∴OD∥AC,
又∵AC⊥BC,
∴OD⊥BC,
∴BC是⊙O的切线,
(2)解:∵BC与圆相切于点D.
∴BD2=BE BA,
∵BE=2,BD=4,
∴BA=8,
∴AE=AB﹣BE=6,
∴⊙O的半径为3.
20 .如图,在△ABC中,∠C=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,
与边BC交于点F,过点E作EH⊥AB于点H,连接BE
(1)求证:EH=EC;
(2)若AB=4,sinA=,求AD的长.
【答案】(1)证明见解析(2)
【分析】(1)连接OE,易证OE∥BC,继而结合已知证明∠CBE=∠EBO,
然后利用角平分线的性质即可证得EH=EC;
由sinA==,设OE=2a,AO=3a(a≠0),根据AB的长可求得a的值,
再根据AD=AB-BD即可求得答案.
【详解】(1)如图,连接OE,
∵AC与⊙O相切,
∴OE⊥AC,且BC⊥AC,
∴OE∥BC
∴∠CBE=∠OEB,
∵EO=OB,
∴∠EBO=∠OEB
∴∠CBE=∠EBO,且CE⊥BC,EH⊥AB,
∴CE=EH
(2)∵sinA==,
∴设OE=2a,AO=3a,(a≠0)
∴OB=OE=2a,
∵AB=AO+OB=3a+2a=4
∴a=,
∵AD=AB﹣BD=4﹣4a
∴AD=.
21.如图,为的直径,C为上的中点,于的延长线交于点E.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
【答案】(1)见解析
(2).
【分析】本题考查了切线的判定以及圆周角定理和扇形的面积公式.
连接,利用半径相等、圆周角定理求得,推出,
从而得到,即可证明是的切线;
设半径为r,利用勾股定理得到,解得,
再计算出,然后根据扇形的面积公式,利用进行计算即可.
【详解】(1)证明:连接,如图,
∵,
∴,
∵C为上的中点,即,
∴,
∴,
∴,
∵,
∴,
∵点C在上,
∴是的切线;
(2)解:连接,设半径为r,
在中,∵,
∴,
解得,
∴,
则,即点B是斜边的中点,
∴,
∴,
∴是等边三角形,
∴,
∴.
22 .如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,
过点P作PD⊥OP交⊙O于点D.
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当弧DC=弧AC时,延长AB至点E,使BE=AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
【答案】(1)2;(2)①证明见解析;②3﹣3.
【分析】(1)根据题意首先得出半径长,再利用锐角三角三角函数关系得出OP,PD的长;
(2)①首先得出△OBD是等边三角形,进而得出∠ODE=∠OFB=90°,求出答案即可;
②首先求出CF的长,进而利用直角三角形的性质得出PF的长,进而得出答案.
【详解】解:(1)如图2,连接OD,
∵OP⊥PD,PD//AB,
∴∠POB=90°,
∵⊙O的直径AB=12,
∴OB=OD=6,
在Rt△POB中,∠ABC=30°,
∴OP=OB tan30°=6×=2,
在Rt△POD中,
PD=;
(2)①如图3,连接OD,交CB于点F,连接BD,
∵,
∴∠DBC=∠ABC=30°,
∴∠ABD=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴OD⊥FB,OB=BD, ∠OBD=∠ODB=60°,
∵BE=AB,
∴OB=BE,
∴BD=BE,
∴∠E=∠BDE=∠OBD=30°,
∴∠E=∠ABC,
∴BF//ED,
∴∠ODE=∠OFB=90°,
∴DE是⊙O的切线;
②由①知,OD⊥BC,
∴CF=FB=OB cos30°=6×=3,
在Rt△POD中,OF=DF,
∴PF=DO=3(直角三角形斜边上的中线,等于斜边的一半),
∴CP=CF﹣PF=3﹣3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
