5.4抛体运动的规律课件(共27张PPT)高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 5.4抛体运动的规律课件(共27张PPT)高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 55.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-19 12:30:52 | ||
图片预览





文档简介
(共27张PPT)
5.4抛体运动的规律
第五章
抛体运动
篮球、铅球、标枪以及炮弹的运动有什么特点?
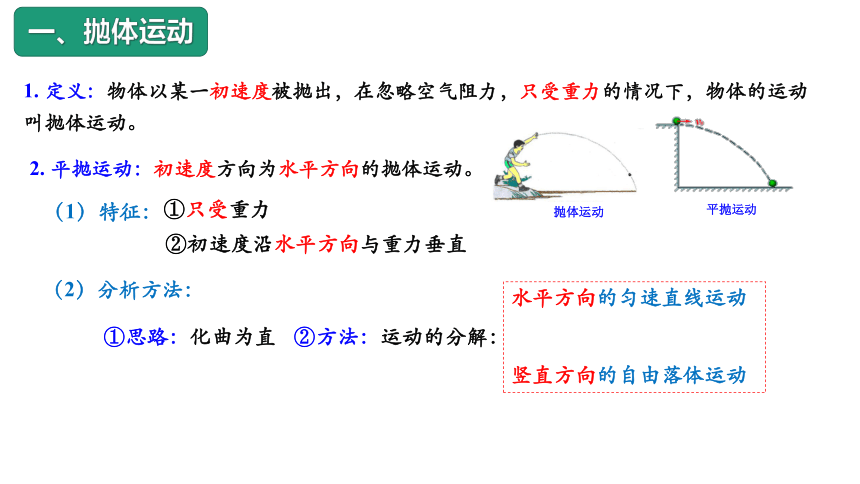
1. 定义:物体以某一初速度被抛出,在忽略空气阻力,只受重力的情况下,物体的运动叫抛体运动。
2. 平抛运动:初速度方向为水平方向的抛体运动。
平抛运动
抛体运动
一、抛体运动
②初速度沿水平方向与重力垂直
(1)特征:
①只受重力
思考: 在排球比赛中,你是否曾为排球下网或者出界而感到惋惜?如果运动员沿水平方向击球,在不计空气阻力的情况下,要使排球既能过网,又不出界,需要考虑哪些因素?如何估算球落地时的速度大小?
1. 定义:物体以某一初速度被抛出,在忽略空气阻力,只受重力的情况下,物体的运动叫抛体运动。
2. 平抛运动:初速度方向为水平方向的抛体运动。
平抛运动
抛体运动
一、抛体运动
②初速度沿水平方向与重力垂直
(1)特征:
①只受重力
(2)分析方法:
①思路:化曲为直
②方法:运动的分解:
水平方向的匀速直线运动
竖直方向的自由落体运动
v
A
O
x
y
t
θ
vx
vy
v0
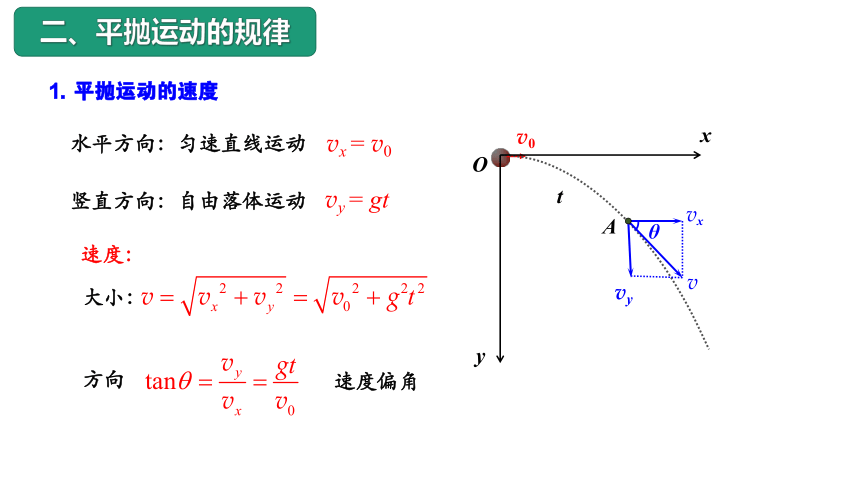
vx = v0
vy = gt
方向
速度:
水平方向:匀速直线运动
竖直方向:自由落体运动
二、平抛运动的规律
1. 平抛运动的速度
大小:
速度偏角
【课本例题 例1】将一个物体以 10 m/s 的速度从 10 m 的高度水平抛出,落地时它的速度方向与水平地面的夹角 θ 是多少?不计空气阻力,g 取 10 m/s2。
水平方向
物体落地时速度与水平地面的夹角 θ 是 55°
解析:
竖直方向
即θ = 55°
A
O
x
y
t
v0
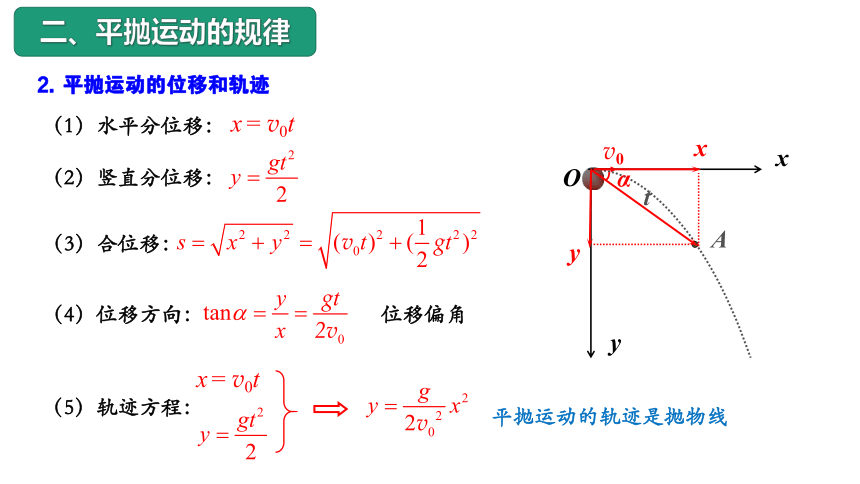
x = v0t
(4)位移方向:
α
x
y
(3)合位移:
(1)水平分位移:
(2)竖直分位移:
(5)轨迹方程:
x = v0t
平抛运动的轨迹是抛物线
2. 平抛运动的位移和轨迹
二、平抛运动的规律
位移偏角
①水平方向:匀速直线运动
②竖直方向:自由落体运动
①速度:
②位移:
3. 平抛运动的规律
二、平抛运动的规律
(1)分运动规律
(2)合运动规律
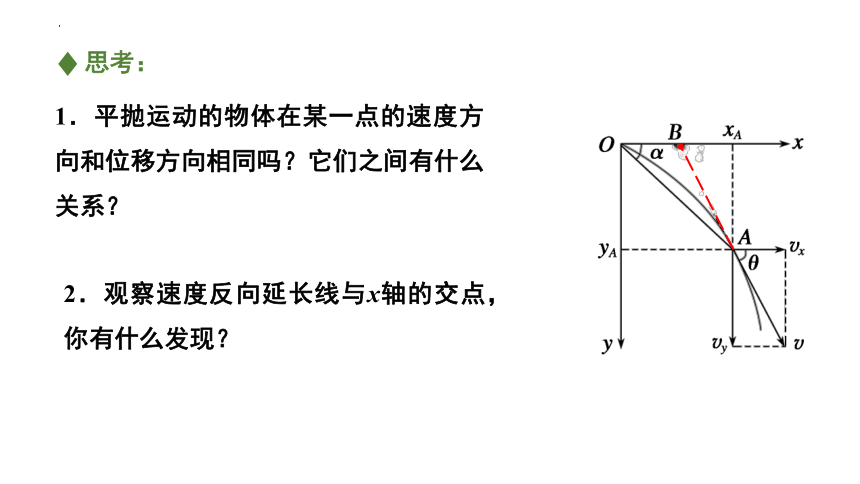
1.平抛运动的物体在某一点的速度方向和位移方向相同吗?它们之间有什么关系?
思考:
2.观察速度反向延长线与x轴的交点,你有什么发现?
推论1:做平抛运动的物体,设其位移偏向角为α,速度偏向角为θ,则在任意时刻、任意位置有tanθ=2tanα。
证明:
(θ≠2α)
得:
α
vx
vy
v
O
x
y
v0
P (x,y)
平抛运动的推论
3. 平抛运动的规律
二、平抛运动的规律
(1)分运动规律
(2)合运动规律
(3)平抛运动的两个推论:
推论2:做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图。
证明:
平抛运动的推论
3. 平抛运动的规律
二、平抛运动的规律
(1)分运动规律
(2)合运动规律
(3)平抛运动的两个推论:
O
y
B
x
A
P (x,y)
v0
l
θ
α
vx
α
v
vy
O′
α
θ
θ
(4)平抛运动速度变化情况
B
O
x
y
v0
vA
A
vB
vC
C
3. 平抛运动的规律
二、平抛运动的规律
v0
vA
vB
vC
任意相等时间 Δt 内的速度变化量相同。
Δv = gΔt
方向恒为竖直向下
(1)分运动规律
(2)合运动规律
(3)平抛运动的两个推论:
【课本例题 例2】如图所示,某同学利用无人机玩“投弹”游戏。无人机以 v0=2 m/s 的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离 h=20 m,空气阻力忽略不计,g 取 10 m/s2。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
解 :(1)以小球从无人机释放时的位置为原点 O 建立平面直角坐标系如图所示,x 轴沿初速度方向,y 轴竖直向下。设小球的落地点为 P,下落的时间为 t.
(2)因此,小球落地点与释放点之间的水平距离
物理量 表达式 影响因素
运动时间 t= 只由高度决定,与初速度无关
水平位移 (射程) x=v0t=v0 由初速度和高度共同决定
落地速度 v=, 与水平方向的夹角为θ tan θ== 由初速度和高度共同决定
(5)平抛运动中几个决定关系
二、平抛运动的规律
3. 平抛运动的规律
(2)初速度特点:水平方向:vx=v0cosθ 做匀速直线运动;
竖直方向:v0y=v0sinθ 竖直上抛运动。
(1)受力特点:
水平方向:不受力,加速度为0;
竖直方向:只受重力,加速度为g。
三、一般的抛体运动:斜抛运动
1.定义:
斜上抛
斜下抛
2.特点:
(3)速度变化特点:
Δv=gΔt 方向均竖直向下
(4).对称性特点(斜上抛)
②时间对称:关于过轨迹最高点的竖直线对称的曲线上升时间等于下降时间。
①速度对称:轨迹上关于过轨迹最高点的竖直线对称的两点速度大小相等,水平方向速度相同,竖直方向速度等大反向。
③轨迹对称:其运动轨迹关于过最高点的竖直线对称。
三、一般的抛体运动:斜抛运动
1.定义:
2.特点:
(1)受力特点
(2)初速度特点
(3)速度变化特点
三、一般的抛体运动:斜抛运动
1.定义
2.特点
3.规律
位移:x=voxt= v0tcosθ
速度:vy=v0y-gt=v0sin θ-gt
速度:vx=v0x=v0cosθ
合速度大小:
合速度方向:
合位移大小:
合位移方向:
匀速直线运动
X轴:
竖直上抛运动
Y轴:
分
解
位移:
v0y
v0
x
v0x
y
0
v
vx
vy
s
y
x
(1)从抛出点到最高点时间t(vy=0)
(2)从抛出点回落到等高点时间T(对称性分析)
由v=v0+at得
三、一般的抛体运动:斜抛运动
1.定义
2.特点
3.规律
4.结论
(3)上升最大高度(射高)H
由v2-v02=2ax得
(4)水平方向的位移(射程)
即θ=45°时x最大
三、一般的抛体运动:斜抛运动
1.定义
2.特点
3.规律
4.结论
四、与斜面、弧面相关的平抛运动
实例1:
实例2:
四、与斜面、弧面相关的平抛运动
实例3:从斜面顶点水平抛出且落在斜面上
四、与斜面、弧面相关的平抛运动
实例4:
五、平抛运动的临界问题
与平抛运动相关的临界情况
(1)有些题目中“刚好”“恰好”“正好”等字眼,明显表明题述的过程中存在临界点.
(2)如题目中有“取值范围”“多长时间”“多大距离”等词语,表明题述过程中存在着“起止点”,而这些“起止点”往往就是临界点.
(3)若题目中有“最大”“最小”“至多”“至少”等字眼,表明题述过程中存在着极值,这些极值也往往是临界点.
解析:
【例题3】如图所示,排球场的长为18 m,球网的高度为2 m.运动员站在离网3 m远的线上,正对球网竖直跳起,把球垂直于网水平击出.(取g=10 m/s2,不计空气阻力)
(1)设击球点的高度为2.5 m,问球被水平击出时的速度v0在什么范围内才能使球既不触网也不出界?
五、平抛运动的临界问题
解析:
【例题3】如图所示,排球场的长为18 m,球网的高度为2 m.运动员站在离网3 m远的线上,正对球网竖直跳起,把球垂直于网水平击出.(取g=10 m/s2,不计空气阻力)
(2)若击球点的高度小于某个值,那么无论球被水平击出时的速度为多大,球不是触网就是出界,试求出此高度.
如图乙所示为排球恰不触网也恰不出界的临界轨迹.设击球点的高度为h,根据平抛运动的规律有
x1=3 m,x1=v0t1′ ⑤
x2=3 m+9 m=12 m,x2=v0t2′⑦
h1′=h-2 m,h1′= gt1′2 ⑥
h2′=h= gt2′2 ⑧
联立⑤⑥⑦⑧式可得,高度h= m.
五、平抛运动的临界问题
六、类平抛运动
1.类平抛运动的特点
(1)物体在某方向做匀速直线运动,在垂直匀速直线运动的方向上做初速度为零的匀加速直线运动.
(2)受力特点:物体所受的合力为恒力,且与初速度的方向垂直.
(3)运动特点:在初速度v0方向做匀速直线运动,在合外力方向做初速度为零的匀加速直线运动,加速度 a=
不同点 类平抛运动 平抛运动
运动平面 任意平面 竖直面
初速度方向 任意方向 水平方向
加速度 a=,与初速度方向垂直 重力加速度g,竖直向下
2.类平抛运动与平抛运动的区别
3.研究方法:分解运动,化曲为直
【例题4】如图所示的光滑固定斜面长为l、宽为b、倾角为θ,一物块(可看成质点)沿斜面左上方顶点P水平射入,恰好从底端Q点离开斜面,试求:(重力加速度为g,不计空气阻力)
(1)物块由P运动到Q所用的时间t;
(2)物块由P点水平射入时的初速度v0;
(3)物块离开Q点时速度的大小v.
(1)沿斜面向下的方向有mgsinθ=ma,l=at2
联立解得:t=.
解析:
(2)沿水平方向有b=v0t v0==b
(3)物块离开Q点时的速度大小
v===
六、类平抛运动
5.4抛体运动的规律
第五章
抛体运动
篮球、铅球、标枪以及炮弹的运动有什么特点?
1. 定义:物体以某一初速度被抛出,在忽略空气阻力,只受重力的情况下,物体的运动叫抛体运动。
2. 平抛运动:初速度方向为水平方向的抛体运动。
平抛运动
抛体运动
一、抛体运动
②初速度沿水平方向与重力垂直
(1)特征:
①只受重力
思考: 在排球比赛中,你是否曾为排球下网或者出界而感到惋惜?如果运动员沿水平方向击球,在不计空气阻力的情况下,要使排球既能过网,又不出界,需要考虑哪些因素?如何估算球落地时的速度大小?
1. 定义:物体以某一初速度被抛出,在忽略空气阻力,只受重力的情况下,物体的运动叫抛体运动。
2. 平抛运动:初速度方向为水平方向的抛体运动。
平抛运动
抛体运动
一、抛体运动
②初速度沿水平方向与重力垂直
(1)特征:
①只受重力
(2)分析方法:
①思路:化曲为直
②方法:运动的分解:
水平方向的匀速直线运动
竖直方向的自由落体运动
v
A
O
x
y
t
θ
vx
vy
v0
vx = v0
vy = gt
方向
速度:
水平方向:匀速直线运动
竖直方向:自由落体运动
二、平抛运动的规律
1. 平抛运动的速度
大小:
速度偏角
【课本例题 例1】将一个物体以 10 m/s 的速度从 10 m 的高度水平抛出,落地时它的速度方向与水平地面的夹角 θ 是多少?不计空气阻力,g 取 10 m/s2。
水平方向
物体落地时速度与水平地面的夹角 θ 是 55°
解析:
竖直方向
即θ = 55°
A
O
x
y
t
v0
x = v0t
(4)位移方向:
α
x
y
(3)合位移:
(1)水平分位移:
(2)竖直分位移:
(5)轨迹方程:
x = v0t
平抛运动的轨迹是抛物线
2. 平抛运动的位移和轨迹
二、平抛运动的规律
位移偏角
①水平方向:匀速直线运动
②竖直方向:自由落体运动
①速度:
②位移:
3. 平抛运动的规律
二、平抛运动的规律
(1)分运动规律
(2)合运动规律
1.平抛运动的物体在某一点的速度方向和位移方向相同吗?它们之间有什么关系?
思考:
2.观察速度反向延长线与x轴的交点,你有什么发现?
推论1:做平抛运动的物体,设其位移偏向角为α,速度偏向角为θ,则在任意时刻、任意位置有tanθ=2tanα。
证明:
(θ≠2α)
得:
α
vx
vy
v
O
x
y
v0
P (x,y)
平抛运动的推论
3. 平抛运动的规律
二、平抛运动的规律
(1)分运动规律
(2)合运动规律
(3)平抛运动的两个推论:
推论2:做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点,如图。
证明:
平抛运动的推论
3. 平抛运动的规律
二、平抛运动的规律
(1)分运动规律
(2)合运动规律
(3)平抛运动的两个推论:
O
y
B
x
A
P (x,y)
v0
l
θ
α
vx
α
v
vy
O′
α
θ
θ
(4)平抛运动速度变化情况
B
O
x
y
v0
vA
A
vB
vC
C
3. 平抛运动的规律
二、平抛运动的规律
v0
vA
vB
vC
任意相等时间 Δt 内的速度变化量相同。
Δv = gΔt
方向恒为竖直向下
(1)分运动规律
(2)合运动规律
(3)平抛运动的两个推论:
【课本例题 例2】如图所示,某同学利用无人机玩“投弹”游戏。无人机以 v0=2 m/s 的速度水平向右匀速飞行,在某时刻释放了一个小球。此时无人机到水平地面的距离 h=20 m,空气阻力忽略不计,g 取 10 m/s2。
(1)求小球下落的时间。
(2)求小球释放点与落地点之间的水平距离。
解 :(1)以小球从无人机释放时的位置为原点 O 建立平面直角坐标系如图所示,x 轴沿初速度方向,y 轴竖直向下。设小球的落地点为 P,下落的时间为 t.
(2)因此,小球落地点与释放点之间的水平距离
物理量 表达式 影响因素
运动时间 t= 只由高度决定,与初速度无关
水平位移 (射程) x=v0t=v0 由初速度和高度共同决定
落地速度 v=, 与水平方向的夹角为θ tan θ== 由初速度和高度共同决定
(5)平抛运动中几个决定关系
二、平抛运动的规律
3. 平抛运动的规律
(2)初速度特点:水平方向:vx=v0cosθ 做匀速直线运动;
竖直方向:v0y=v0sinθ 竖直上抛运动。
(1)受力特点:
水平方向:不受力,加速度为0;
竖直方向:只受重力,加速度为g。
三、一般的抛体运动:斜抛运动
1.定义:
斜上抛
斜下抛
2.特点:
(3)速度变化特点:
Δv=gΔt 方向均竖直向下
(4).对称性特点(斜上抛)
②时间对称:关于过轨迹最高点的竖直线对称的曲线上升时间等于下降时间。
①速度对称:轨迹上关于过轨迹最高点的竖直线对称的两点速度大小相等,水平方向速度相同,竖直方向速度等大反向。
③轨迹对称:其运动轨迹关于过最高点的竖直线对称。
三、一般的抛体运动:斜抛运动
1.定义:
2.特点:
(1)受力特点
(2)初速度特点
(3)速度变化特点
三、一般的抛体运动:斜抛运动
1.定义
2.特点
3.规律
位移:x=voxt= v0tcosθ
速度:vy=v0y-gt=v0sin θ-gt
速度:vx=v0x=v0cosθ
合速度大小:
合速度方向:
合位移大小:
合位移方向:
匀速直线运动
X轴:
竖直上抛运动
Y轴:
分
解
位移:
v0y
v0
x
v0x
y
0
v
vx
vy
s
y
x
(1)从抛出点到最高点时间t(vy=0)
(2)从抛出点回落到等高点时间T(对称性分析)
由v=v0+at得
三、一般的抛体运动:斜抛运动
1.定义
2.特点
3.规律
4.结论
(3)上升最大高度(射高)H
由v2-v02=2ax得
(4)水平方向的位移(射程)
即θ=45°时x最大
三、一般的抛体运动:斜抛运动
1.定义
2.特点
3.规律
4.结论
四、与斜面、弧面相关的平抛运动
实例1:
实例2:
四、与斜面、弧面相关的平抛运动
实例3:从斜面顶点水平抛出且落在斜面上
四、与斜面、弧面相关的平抛运动
实例4:
五、平抛运动的临界问题
与平抛运动相关的临界情况
(1)有些题目中“刚好”“恰好”“正好”等字眼,明显表明题述的过程中存在临界点.
(2)如题目中有“取值范围”“多长时间”“多大距离”等词语,表明题述过程中存在着“起止点”,而这些“起止点”往往就是临界点.
(3)若题目中有“最大”“最小”“至多”“至少”等字眼,表明题述过程中存在着极值,这些极值也往往是临界点.
解析:
【例题3】如图所示,排球场的长为18 m,球网的高度为2 m.运动员站在离网3 m远的线上,正对球网竖直跳起,把球垂直于网水平击出.(取g=10 m/s2,不计空气阻力)
(1)设击球点的高度为2.5 m,问球被水平击出时的速度v0在什么范围内才能使球既不触网也不出界?
五、平抛运动的临界问题
解析:
【例题3】如图所示,排球场的长为18 m,球网的高度为2 m.运动员站在离网3 m远的线上,正对球网竖直跳起,把球垂直于网水平击出.(取g=10 m/s2,不计空气阻力)
(2)若击球点的高度小于某个值,那么无论球被水平击出时的速度为多大,球不是触网就是出界,试求出此高度.
如图乙所示为排球恰不触网也恰不出界的临界轨迹.设击球点的高度为h,根据平抛运动的规律有
x1=3 m,x1=v0t1′ ⑤
x2=3 m+9 m=12 m,x2=v0t2′⑦
h1′=h-2 m,h1′= gt1′2 ⑥
h2′=h= gt2′2 ⑧
联立⑤⑥⑦⑧式可得,高度h= m.
五、平抛运动的临界问题
六、类平抛运动
1.类平抛运动的特点
(1)物体在某方向做匀速直线运动,在垂直匀速直线运动的方向上做初速度为零的匀加速直线运动.
(2)受力特点:物体所受的合力为恒力,且与初速度的方向垂直.
(3)运动特点:在初速度v0方向做匀速直线运动,在合外力方向做初速度为零的匀加速直线运动,加速度 a=
不同点 类平抛运动 平抛运动
运动平面 任意平面 竖直面
初速度方向 任意方向 水平方向
加速度 a=,与初速度方向垂直 重力加速度g,竖直向下
2.类平抛运动与平抛运动的区别
3.研究方法:分解运动,化曲为直
【例题4】如图所示的光滑固定斜面长为l、宽为b、倾角为θ,一物块(可看成质点)沿斜面左上方顶点P水平射入,恰好从底端Q点离开斜面,试求:(重力加速度为g,不计空气阻力)
(1)物块由P运动到Q所用的时间t;
(2)物块由P点水平射入时的初速度v0;
(3)物块离开Q点时速度的大小v.
(1)沿斜面向下的方向有mgsinθ=ma,l=at2
联立解得:t=.
解析:
(2)沿水平方向有b=v0t v0==b
(3)物块离开Q点时的速度大小
v===
六、类平抛运动
