【期末复习专题】几何小实践(复习课件)(共26张PPT)-2023-2024学年五年级数学上册期末核心考点集训(沪教版)
文档属性
| 名称 | 【期末复习专题】几何小实践(复习课件)(共26张PPT)-2023-2024学年五年级数学上册期末核心考点集训(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
几何小实践复习专题
沪教版五年级数学上册
平行四边形和平行四边形的面积
1
三角形的面积
2
梯形和梯形的面积
3
组合图形的面积
4
几何小实践
平行四边形
三角形的面积
1、三角形的面积=底×高÷2,字母表示:S=ah÷2;
2、直角三角形的面积=直角边×直角边÷2。
1、两组对边分别平行的四边形叫做平行四边形。
2、平行四边形可以用符号“ ”表示,如左图平行四边形ABCD可记作: ABCD。
2、从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。
3、平行四边形的两组对边分别平行并且相等。两组对角分别相等。
4、特性:平行四边形易变形,具有不稳定性。
平行四边形
平行四边形的面积
平行四边形的面积=底×高,字母表示:S=ah。
特殊的平行四边形
1、长方形的两组对边分别平行,是特殊的平行四边形。
2、当长方形的长和宽相等时,它就成为正方形。正方形是长和宽相等的特殊的长方形。
几何小实践
梯形
梯形的面积
梯形的面积=(上底+下底)×高÷2
字母表示:S=(a+b)h÷2
1、定义:只有一组对边平行的四边形,叫做梯形。
2、在梯形里,互相平行的一组对边分别叫做梯形的上底和下底,不平行的一组对边叫做梯形的腰。
3、从上底上一点向下底画垂线,这点和垂足之间的线段叫做梯形的高。
梯形
特殊的梯形
1、两腰相等的梯形叫做等腰梯形。
2、有一个角是直角的梯形叫做直角梯形。
组合图形的面积
(阴影部分面积)
通过平移、割补等方法,将组合图形转化成已经学过的简单图形的面积问题,通过求几个简单的图形面积的和或差来解决组合图形(或阴影部分)的面积问题。
平行四边形
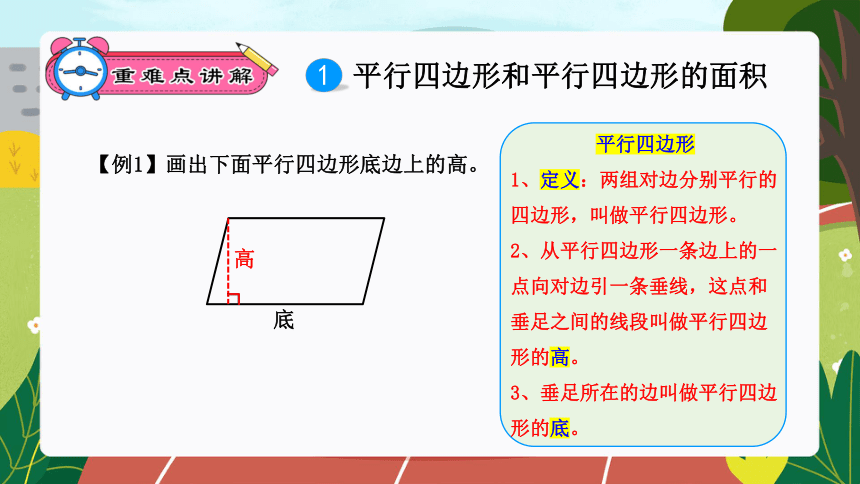
1、定义:两组对边分别平行的四边形,叫做平行四边形。
2、从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高。
3、垂足所在的边叫做平行四边形的底。
平行四边形和平行四边形的面积
1
【例1】画出下面平行四边形底边上的高。
底
高
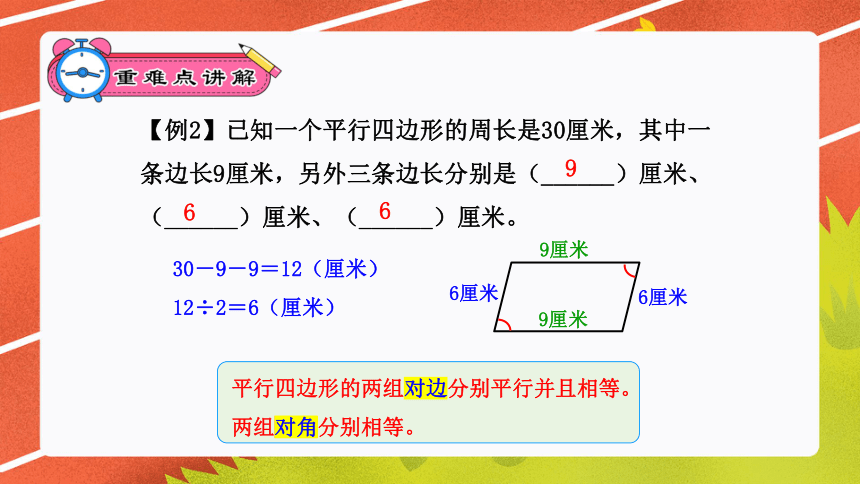
平行四边形的两组对边分别平行并且相等。
两组对角分别相等。
【例2】已知一个平行四边形的周长是30厘米,其中一条边长9厘米,另外三条边长分别是(______)厘米、(______)厘米、(______)厘米。
9
30-9-9=12(厘米)
12÷2=6(厘米)
9厘米
9厘米
6厘米
6厘米
6
6
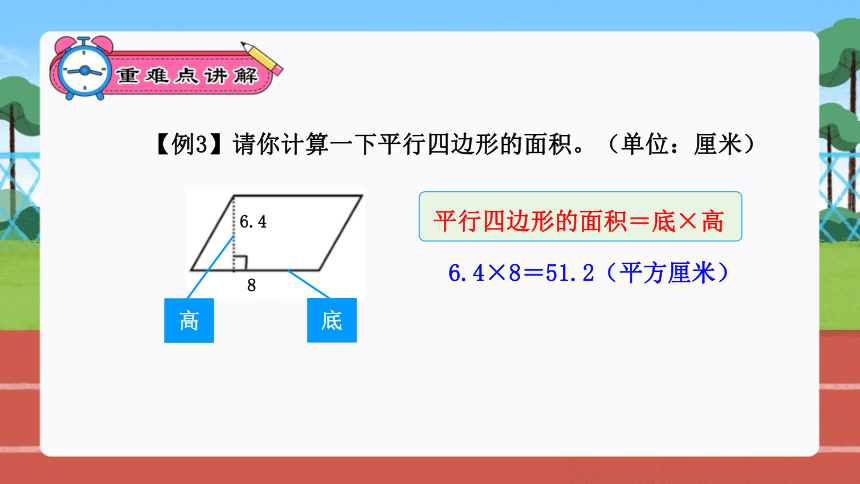
【例3】请你计算一下平行四边形的面积。(单位:厘米)
6.4×8=51.2(平方厘米)
6.4
8
底
高
平行四边形的面积=底×高
【例4】要给一块底是90米,高是50米的平行四边形形状的绿地撒农药,如果每平方米需要30克药粉,这块绿地一共需要多少千克药粉?
【分析】绿地的面积(平行四边形面积)=底×高
药粉总克数=每平方米需要的药粉克数×绿地的面积
90×50=4500(平方米)
4500×30=135000(克)=135(千克)
答:这块绿地一共需要135千克药粉。
1、一个长为9厘米、宽为4厘米的长方形和一个高为12厘米的平行四边形的面积相等,那么这个平行四边形的底是多少厘米?
【分析】长方形的面积=长×宽
平行四边形的底=平行四边形的面积÷高
9×4=36(平方厘米)
36÷12=3(厘米)
答:这个平行四边形的底是3厘米。
三角形的面积
2
【例5】有一个三角形的铁片,它的高是12分米,底是高的4倍,这块三角形铁片的面积是多少平方分米?
【分析】三角形的底=高×4
三角形面积=底×高÷2
4×12=48(分米)
48×12÷2
=576÷2
=288(平方分米)
答:这块三角形铁片的面积是288平方分米。
底
高
三形的面积=底×高÷2
【例6】要给一块底是3米,高是2.2米的三角形广告牌的正反两面都刷上油漆。如果每平方米需要刷2千克油漆,那么将这个广告牌刷好,购买13千克油漆够不够?
【分析】三角形广告牌的面积=底×高÷2
油漆千克总数=每平方米需要刷油漆的数量×三角形广告牌的面积×2
3×2.2÷2
=6.6÷2
=3.3(平方米)
3.3×2×2
=6.6×2
=13.2(千克)
13.2千克>13千克
答:购买13千克油漆不够。
1、在一块高是40米,底是30米的三角形空地里种苹果树,如果平均每棵苹果树占地6平方米,这块空地一共可以种多少棵苹果树?
【分析】三角形空地的面积=底×高÷2
苹果树棵数=三角形空地的面积÷每棵苹果树的占地面积
40×30÷2
=1200÷2
=600(平方米)
600÷6=100(棵)
答:这块空地一共可以种100棵苹果树。
2、刘伯伯需要买一块底长26分米,高是20分米的三角形柚木木板,如果每平方分米柚木木板的售价是2元,刘伯伯买这块柚木木板需要多少元?
【分析】三角形木板的面积=底×高÷2
木板总价=木板每平方分米的售价×三角形木板的面积
26×20÷2
=520÷2
=260(平方米)
260×2=520(元)
答:刘伯伯买这块木板需要520元。
梯形和梯形的面积
3
上底
互相平行的一组对边,较短的边叫做梯形的上底。
下底
互相平行的一组对边,较长的边叫做梯形的下底。
腰
不平行的那组对边,分别叫做梯形的腰。
高
从梯形上底任取一个点,向下底引一条垂线,这个点和垂足之间的线段叫做梯形的高。
只有一组对边平行的四边形叫梯形。
两腰相等的梯形叫做等腰梯形。
有一个角是直角的梯形叫做直角梯形。
【例7】有一个梯形,它的上底是30厘米,下底是60厘米,高是25厘米,这个梯形的面积是多少平方厘米?
(30+60)×25÷2
=90×25÷2
=2250÷2
=1125(平方厘米)
答:这个梯形的面积是1125平方厘米。
梯形的面积=(上底+下底)×高÷2
上底
下底
高
【例8】在一块梯形菜地种蔬菜,菜地的上底长8.6米,下底长12.4米,高是6米,每平方米可以收获20千克蔬菜,这块菜地的一共可以收获多少千克蔬菜?
(8.6+12.4)×6÷2
=21×6÷2
=126÷2
=63(平方米)
63×20=1260(千克)
答:这块菜地的一共可以收获1260千克蔬菜。
【分析】梯形菜地的面积=(上底+下底)×高÷2
蔬菜千克总数=每平方米收获蔬菜的千克数×梯形菜地的面积
1、已知一张梯形卡纸的上底是8厘米,下底是上底的1.2倍,高是1.5厘米,这张梯形的面积是多少平方厘米?
8×1.2=9.6(厘米)
(8+9.6)×1.5÷2
=17.6×1.5÷2
=26.4÷2
=13.2(平方厘米)
答:这张梯形卡纸的面积是13.2平方厘米。
【分析】梯形菜地的面积=(上底+下底)×高÷2
只有一组对边平行的四边形。
有一个角是直角的梯形
两腰相等的梯形
两组对边分别平行的四边形
四个角都是直角的四边形
四个角都是直角,并且四条边都相等的四边形
组合图形的面积
4
1、求平面的组合图形面积时可以合理地进行割或补,使组合图形的面积转化成我们学过的基础图形的面积进行求解。
2、求组合图形的方法:
(1)分割法:
把一个组合图形分割成几个基础图形(平行四边形、正方形、长方形、三角形和梯形、圆等),分别求出面积,再进行求和。
(2)添补法:
把一个组合图形补成一个基础图形,再从这个基础图形的面积减去几个基础图形的面积,从而求出它们的面积差。
【例9】你会求下面这个图形的面积吗?
【分析】长方形面积=长×宽
梯形的面积=(上底+下底)×高÷2
组合图形面积=长方形面积+梯形面积
8×12=96(平方厘米)
(6+12)×(14-8)÷2
=18×6÷2
=54(平方厘米)
96+54=150(平方厘米)
8厘米
12厘米
6厘米
14厘米
【例10】求下面这个图形的面积。
6厘米
10厘米
16厘米
13厘米
16厘米
【分析】长方形面积=长×宽
三角形的面积=底×高÷2
组合图形面积=长方形面积-三角形面积
16×13=208(平方厘米)
6×10÷2
=60÷2
=30(平方厘米)
208-30=178(平方厘米)
1、已知一个平行四边形的高是5厘米,底是6厘米,如果一个三角形和这个平行四边形的底和面积都分别相等,则三角形的高是( )厘米。
A、3
B、6
C、10
C
2、已知一个平行四边形的面积是288平方厘米,高是16厘米,那么底是( )厘米。
A、36
B、18
C、9
B
3、给一块底是1.5米,高是1.2米的三角形的交通标志牌的一面刷上油漆,每平方米需要用油漆1.6千克,一共需要多少千克油漆?
1.5×1.2÷2
=1.8÷2
=0.9(平方米)
0.9×1.6=1.44(千克)
答:一共需要1.44千克油漆。
4、在一块上底为20米,下底为60米,高为15米的梯形草地中间有一个长为8米,宽为5米的长方形花坛(如图)。那么草地的面积是多少平方米?
(20+60)×15÷2
=80×15÷2
=600(平方米)
8×5=40(平方米)
600-40=560(平方米)
答:草地的面积是560平方米。
每一份努力,都将在学习中得到最好的回报。加油!
几何小实践复习专题
沪教版五年级数学上册
平行四边形和平行四边形的面积
1
三角形的面积
2
梯形和梯形的面积
3
组合图形的面积
4
几何小实践
平行四边形
三角形的面积
1、三角形的面积=底×高÷2,字母表示:S=ah÷2;
2、直角三角形的面积=直角边×直角边÷2。
1、两组对边分别平行的四边形叫做平行四边形。
2、平行四边形可以用符号“ ”表示,如左图平行四边形ABCD可记作: ABCD。
2、从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。
3、平行四边形的两组对边分别平行并且相等。两组对角分别相等。
4、特性:平行四边形易变形,具有不稳定性。
平行四边形
平行四边形的面积
平行四边形的面积=底×高,字母表示:S=ah。
特殊的平行四边形
1、长方形的两组对边分别平行,是特殊的平行四边形。
2、当长方形的长和宽相等时,它就成为正方形。正方形是长和宽相等的特殊的长方形。
几何小实践
梯形
梯形的面积
梯形的面积=(上底+下底)×高÷2
字母表示:S=(a+b)h÷2
1、定义:只有一组对边平行的四边形,叫做梯形。
2、在梯形里,互相平行的一组对边分别叫做梯形的上底和下底,不平行的一组对边叫做梯形的腰。
3、从上底上一点向下底画垂线,这点和垂足之间的线段叫做梯形的高。
梯形
特殊的梯形
1、两腰相等的梯形叫做等腰梯形。
2、有一个角是直角的梯形叫做直角梯形。
组合图形的面积
(阴影部分面积)
通过平移、割补等方法,将组合图形转化成已经学过的简单图形的面积问题,通过求几个简单的图形面积的和或差来解决组合图形(或阴影部分)的面积问题。
平行四边形
1、定义:两组对边分别平行的四边形,叫做平行四边形。
2、从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高。
3、垂足所在的边叫做平行四边形的底。
平行四边形和平行四边形的面积
1
【例1】画出下面平行四边形底边上的高。
底
高
平行四边形的两组对边分别平行并且相等。
两组对角分别相等。
【例2】已知一个平行四边形的周长是30厘米,其中一条边长9厘米,另外三条边长分别是(______)厘米、(______)厘米、(______)厘米。
9
30-9-9=12(厘米)
12÷2=6(厘米)
9厘米
9厘米
6厘米
6厘米
6
6
【例3】请你计算一下平行四边形的面积。(单位:厘米)
6.4×8=51.2(平方厘米)
6.4
8
底
高
平行四边形的面积=底×高
【例4】要给一块底是90米,高是50米的平行四边形形状的绿地撒农药,如果每平方米需要30克药粉,这块绿地一共需要多少千克药粉?
【分析】绿地的面积(平行四边形面积)=底×高
药粉总克数=每平方米需要的药粉克数×绿地的面积
90×50=4500(平方米)
4500×30=135000(克)=135(千克)
答:这块绿地一共需要135千克药粉。
1、一个长为9厘米、宽为4厘米的长方形和一个高为12厘米的平行四边形的面积相等,那么这个平行四边形的底是多少厘米?
【分析】长方形的面积=长×宽
平行四边形的底=平行四边形的面积÷高
9×4=36(平方厘米)
36÷12=3(厘米)
答:这个平行四边形的底是3厘米。
三角形的面积
2
【例5】有一个三角形的铁片,它的高是12分米,底是高的4倍,这块三角形铁片的面积是多少平方分米?
【分析】三角形的底=高×4
三角形面积=底×高÷2
4×12=48(分米)
48×12÷2
=576÷2
=288(平方分米)
答:这块三角形铁片的面积是288平方分米。
底
高
三形的面积=底×高÷2
【例6】要给一块底是3米,高是2.2米的三角形广告牌的正反两面都刷上油漆。如果每平方米需要刷2千克油漆,那么将这个广告牌刷好,购买13千克油漆够不够?
【分析】三角形广告牌的面积=底×高÷2
油漆千克总数=每平方米需要刷油漆的数量×三角形广告牌的面积×2
3×2.2÷2
=6.6÷2
=3.3(平方米)
3.3×2×2
=6.6×2
=13.2(千克)
13.2千克>13千克
答:购买13千克油漆不够。
1、在一块高是40米,底是30米的三角形空地里种苹果树,如果平均每棵苹果树占地6平方米,这块空地一共可以种多少棵苹果树?
【分析】三角形空地的面积=底×高÷2
苹果树棵数=三角形空地的面积÷每棵苹果树的占地面积
40×30÷2
=1200÷2
=600(平方米)
600÷6=100(棵)
答:这块空地一共可以种100棵苹果树。
2、刘伯伯需要买一块底长26分米,高是20分米的三角形柚木木板,如果每平方分米柚木木板的售价是2元,刘伯伯买这块柚木木板需要多少元?
【分析】三角形木板的面积=底×高÷2
木板总价=木板每平方分米的售价×三角形木板的面积
26×20÷2
=520÷2
=260(平方米)
260×2=520(元)
答:刘伯伯买这块木板需要520元。
梯形和梯形的面积
3
上底
互相平行的一组对边,较短的边叫做梯形的上底。
下底
互相平行的一组对边,较长的边叫做梯形的下底。
腰
不平行的那组对边,分别叫做梯形的腰。
高
从梯形上底任取一个点,向下底引一条垂线,这个点和垂足之间的线段叫做梯形的高。
只有一组对边平行的四边形叫梯形。
两腰相等的梯形叫做等腰梯形。
有一个角是直角的梯形叫做直角梯形。
【例7】有一个梯形,它的上底是30厘米,下底是60厘米,高是25厘米,这个梯形的面积是多少平方厘米?
(30+60)×25÷2
=90×25÷2
=2250÷2
=1125(平方厘米)
答:这个梯形的面积是1125平方厘米。
梯形的面积=(上底+下底)×高÷2
上底
下底
高
【例8】在一块梯形菜地种蔬菜,菜地的上底长8.6米,下底长12.4米,高是6米,每平方米可以收获20千克蔬菜,这块菜地的一共可以收获多少千克蔬菜?
(8.6+12.4)×6÷2
=21×6÷2
=126÷2
=63(平方米)
63×20=1260(千克)
答:这块菜地的一共可以收获1260千克蔬菜。
【分析】梯形菜地的面积=(上底+下底)×高÷2
蔬菜千克总数=每平方米收获蔬菜的千克数×梯形菜地的面积
1、已知一张梯形卡纸的上底是8厘米,下底是上底的1.2倍,高是1.5厘米,这张梯形的面积是多少平方厘米?
8×1.2=9.6(厘米)
(8+9.6)×1.5÷2
=17.6×1.5÷2
=26.4÷2
=13.2(平方厘米)
答:这张梯形卡纸的面积是13.2平方厘米。
【分析】梯形菜地的面积=(上底+下底)×高÷2
只有一组对边平行的四边形。
有一个角是直角的梯形
两腰相等的梯形
两组对边分别平行的四边形
四个角都是直角的四边形
四个角都是直角,并且四条边都相等的四边形
组合图形的面积
4
1、求平面的组合图形面积时可以合理地进行割或补,使组合图形的面积转化成我们学过的基础图形的面积进行求解。
2、求组合图形的方法:
(1)分割法:
把一个组合图形分割成几个基础图形(平行四边形、正方形、长方形、三角形和梯形、圆等),分别求出面积,再进行求和。
(2)添补法:
把一个组合图形补成一个基础图形,再从这个基础图形的面积减去几个基础图形的面积,从而求出它们的面积差。
【例9】你会求下面这个图形的面积吗?
【分析】长方形面积=长×宽
梯形的面积=(上底+下底)×高÷2
组合图形面积=长方形面积+梯形面积
8×12=96(平方厘米)
(6+12)×(14-8)÷2
=18×6÷2
=54(平方厘米)
96+54=150(平方厘米)
8厘米
12厘米
6厘米
14厘米
【例10】求下面这个图形的面积。
6厘米
10厘米
16厘米
13厘米
16厘米
【分析】长方形面积=长×宽
三角形的面积=底×高÷2
组合图形面积=长方形面积-三角形面积
16×13=208(平方厘米)
6×10÷2
=60÷2
=30(平方厘米)
208-30=178(平方厘米)
1、已知一个平行四边形的高是5厘米,底是6厘米,如果一个三角形和这个平行四边形的底和面积都分别相等,则三角形的高是( )厘米。
A、3
B、6
C、10
C
2、已知一个平行四边形的面积是288平方厘米,高是16厘米,那么底是( )厘米。
A、36
B、18
C、9
B
3、给一块底是1.5米,高是1.2米的三角形的交通标志牌的一面刷上油漆,每平方米需要用油漆1.6千克,一共需要多少千克油漆?
1.5×1.2÷2
=1.8÷2
=0.9(平方米)
0.9×1.6=1.44(千克)
答:一共需要1.44千克油漆。
4、在一块上底为20米,下底为60米,高为15米的梯形草地中间有一个长为8米,宽为5米的长方形花坛(如图)。那么草地的面积是多少平方米?
(20+60)×15÷2
=80×15÷2
=600(平方米)
8×5=40(平方米)
600-40=560(平方米)
答:草地的面积是560平方米。
每一份努力,都将在学习中得到最好的回报。加油!
同课章节目录
