安徽省亳州市2023-2024学年八年级上学期第三次月考数学试题(含答案)
文档属性
| 名称 | 安徽省亳州市2023-2024学年八年级上学期第三次月考数学试题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 00:00:00 | ||
图片预览


文档简介
八年级数学
(沪科版)
注意事项:
1.你拿到的试卷满分150分,考试时间为120分钟.
2.本试卷包括“试题卷”和“答题卷”两部分.“试题卷”共4页,“答题卷”共6页.
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的.
4.考试结束后,请将“试题卷”和“答题卷”一并交回.
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的.
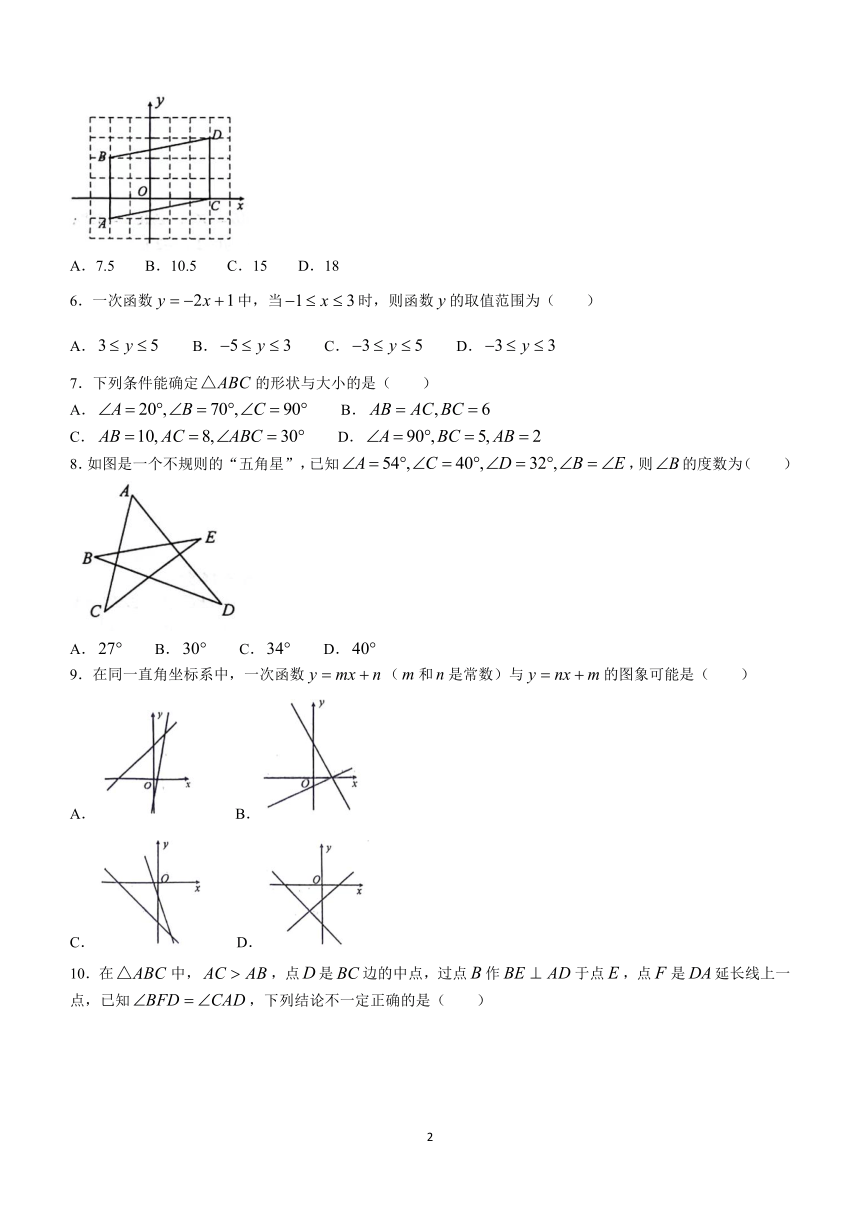
1.在平面直角坐标系中,点到轴的距离是( )
A.4 B.3 C. D.
2.下列图形中,最具有稳定性质的是( )
A. B.
C. D.
3.一次函数的值随的增大而减小;则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,,点共线,已知,则的度数为( )
A. B. C. D.
5.如图,在平面直角坐标系,线段的两个端点坐标依次为,将线段向右平移5个单位,再向上平移1个单位,得到对应线段,则四边形的面积为( )
A.7.5 B.10.5 C.15 D.18
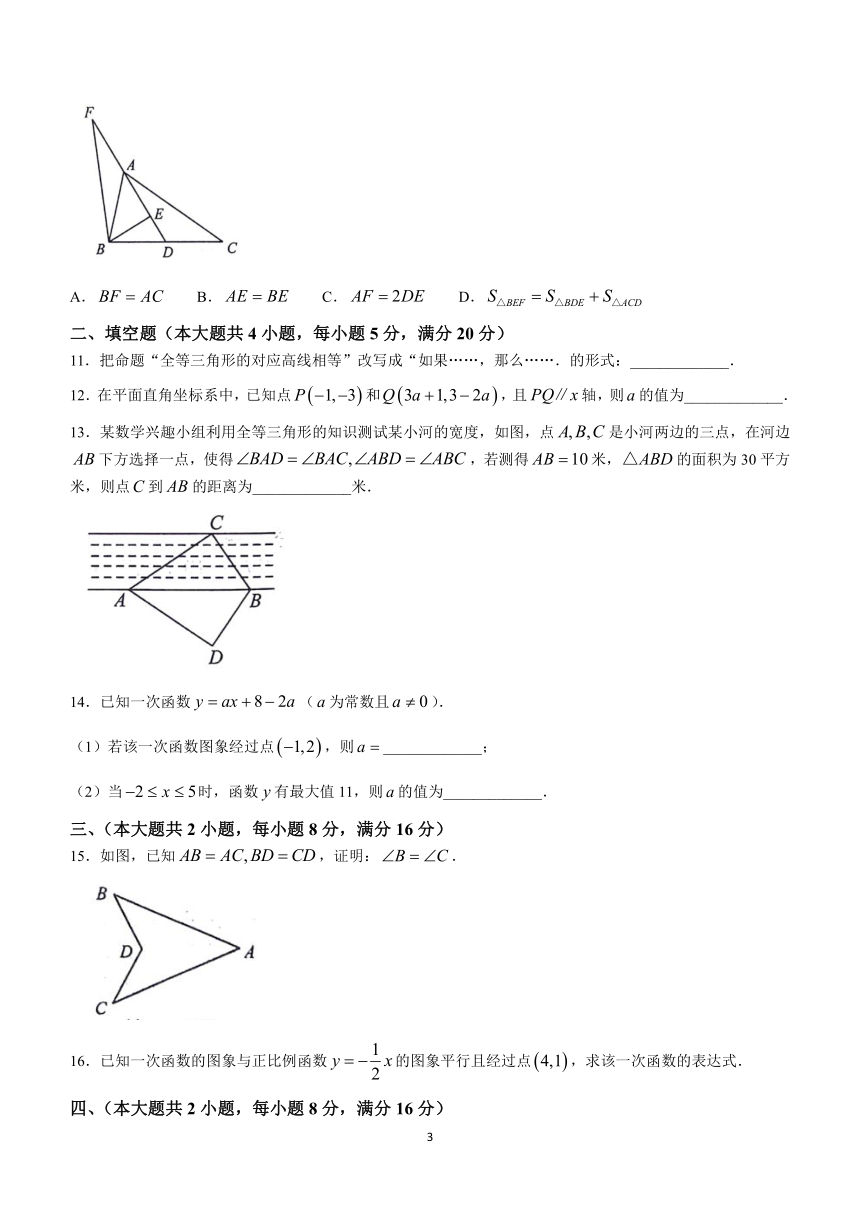
6.一次函数中,当时,则函数的取值范围为( )
A. B. C. D.
7.下列条件能确定的形状与大小的是( )
A. B.
C. D.
8.如图是一个不规则的“五角星”,已知,则的度数为( )
A. B. C. D.
9.在同一直角坐标系中,一次函数(和是常数)与的图象可能是( )
A. B.
C. D.
10.在中,,点是边的中点,过点作于点,点是延长线上一点,已知,下列结论不一定正确的是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
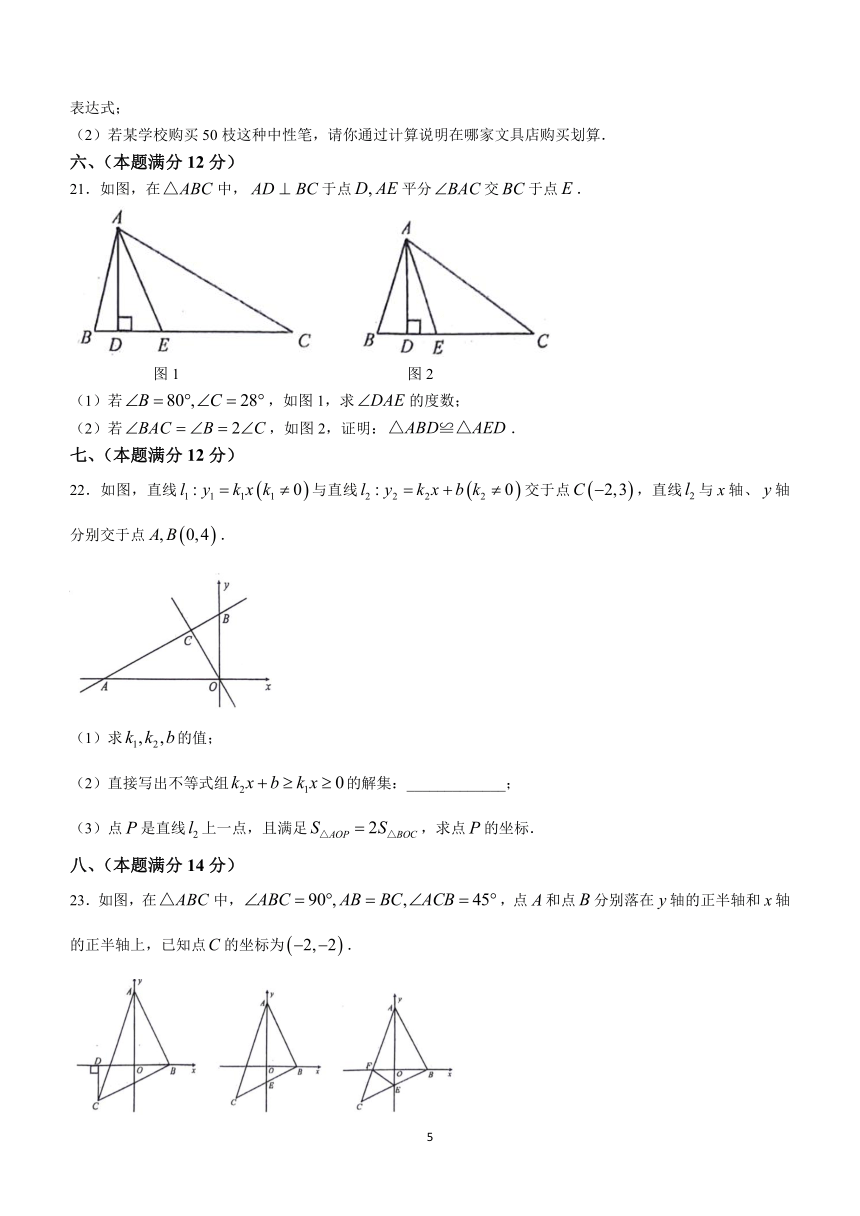
11.把命题“全等三角形的对应高线相等”改写成“如果……,那么…….的形式:_____________.
12.在平面直角坐标系中,已知点和,且轴,则的值为_____________.
13.某数学兴趣小组利用全等三角形的知识测试某小河的宽度,如图,点是小河两边的三点,在河边下方选择一点,使得,若测得米,的面积为30平方米,则点到的距离为_____________米.
14.已知一次函数(为常数且).
(1)若该一次函数图象经过点,则_____________;
(2)当时,函数有最大值11,则的值为_____________.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,已知,证明:.
16.已知一次函数的图象与正比例函数的图象平行且经过点,求该一次函数的表达式.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,点和点的坐标分别为.
(1)将向右平移4个单位,再向下平移2个单位,得到,画出;
(2)用无刻度直尺在网格内画出,使得,并写出点的坐标.
18.如图,在和中,点和点分别是和上的点,与交于点,已知.
(1)证明:;
(2)若,求的度数.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在中,于点,点是上一点,连接并延长交于点,已知.
(1)证明:;
(2)若,求的面积.
20.某种中性笔在甲、乙两家文具店的标价都是4元/支,在“双11”期间,两家文具店都进行了优惠活动.甲文具店:购买不超过20支按原价销售,超出20支的部分按6折销售;乙文具店:不论买多少,全部按八折销售.
(1)分别写出甲、乙两家文具店购买这种中性笔所付总费用(元)与购买支数之间的函数表达式;
(2)若某学校购买50枝这种中性笔,请你通过计算说明在哪家文具店购买划算.
六、(本题满分12分)
21.如图,在中,于点平分交于点.
图1 图2
(1)若,如图1,求的度数;
(2)若,如图2,证明:.
七、(本题满分12分)
22.如图,直线与直线交于点,直线与轴、轴分别交于点.
(1)求的值;
(2)直接写出不等式组的解集:_____________;
(3)点是直线上一点,且满足,求点的坐标.
八、(本题满分14分)
23.如图,在中,,点和点分别落在轴的正半轴和轴的正半轴上,已知点的坐标为.
图1 图2 图3
(1)如图1,过点作轴于点,证明:,并直接写出点的坐标;
(2)如图2,若与轴交于点,证明:是的中线;
(3)如图3,若与轴交于点,连接,探索线段和之间的数量关系,并加以证明.
八年级数学参考答案及评分标准
(沪科版)
一、选择题(本大题共10小题,每小题4分,满分40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D C C B D A C B
10.B 如图,过点作于点,,,又,,,,又,,故选项A、C、D正确,而与不一定相等,故选B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果两个三角形是全等三角形,那么它们的对应高线相等
12.3 13.6
14.(1)2(2)1或
(1)把点代入一次函数的表达式中,得,解得;
(2)当时,随增大而增大,则当时,有最大值,,解得;当时,随增大而减小,则当时,有最大值,,解得.综上所述,的值为1或.
三、(本大题共2小题,每小题8分,满分16分)
15.证明:连接,如图.
.
16.解:由题意可设该一次函数的表达式为,
代入点,得,解得,
该一次函数的表达式为.
四、(本大题共2小题,每小题8分,满分16分)
17.解:(1)如图所示;
(2)如图所示,
点.
18.解:(1)证明:在和中,
,
,
,即;
(2)由(1)可知,
.
五、(本大题共2小题,每小题10分,满分20分)
19.(1)证明:.
在和中,,
,
,又,即;
(2),又,
.
20.解:(1)甲文具店:;
乙文具店:.
(2)当时,(元),
(元),
,
当购买50支这种中性笔时,选择在甲文具店购买划算.
六、(本题满分12分)
21.解:(1)在中,.
平分.
,
;
(2).在中,,
,解得,则,
.
在和中,.
22.解:(1)把点代入,得,解得.2分把点和点代入,得,解得,即和的值分别为;
(2);
(3)当时,,解得,即.
由点的坐标,得.
设点的坐标为,则.
由,得,整理,得,
或,解得或.
当时,;当时,,
点的坐标为或.
八、(本题满分14分)
23.(1)证明:由题意可知,
.
又.
点的坐标为;
(2)如图,过点作轴于点,则.
由(1)可知,
,即点是的中点,是的中线;
(3),理由如下:
如图,在上截取,使得,连接.
在和中,,
,则.
由(2)可知,
.
(沪科版)
注意事项:
1.你拿到的试卷满分150分,考试时间为120分钟.
2.本试卷包括“试题卷”和“答题卷”两部分.“试题卷”共4页,“答题卷”共6页.
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的.
4.考试结束后,请将“试题卷”和“答题卷”一并交回.
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出A、B、C、D四个选项,其中只有一个是正确的.
1.在平面直角坐标系中,点到轴的距离是( )
A.4 B.3 C. D.
2.下列图形中,最具有稳定性质的是( )
A. B.
C. D.
3.一次函数的值随的增大而减小;则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.如图,,点共线,已知,则的度数为( )
A. B. C. D.
5.如图,在平面直角坐标系,线段的两个端点坐标依次为,将线段向右平移5个单位,再向上平移1个单位,得到对应线段,则四边形的面积为( )
A.7.5 B.10.5 C.15 D.18
6.一次函数中,当时,则函数的取值范围为( )
A. B. C. D.
7.下列条件能确定的形状与大小的是( )
A. B.
C. D.
8.如图是一个不规则的“五角星”,已知,则的度数为( )
A. B. C. D.
9.在同一直角坐标系中,一次函数(和是常数)与的图象可能是( )
A. B.
C. D.
10.在中,,点是边的中点,过点作于点,点是延长线上一点,已知,下列结论不一定正确的是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.把命题“全等三角形的对应高线相等”改写成“如果……,那么…….的形式:_____________.
12.在平面直角坐标系中,已知点和,且轴,则的值为_____________.
13.某数学兴趣小组利用全等三角形的知识测试某小河的宽度,如图,点是小河两边的三点,在河边下方选择一点,使得,若测得米,的面积为30平方米,则点到的距离为_____________米.
14.已知一次函数(为常数且).
(1)若该一次函数图象经过点,则_____________;
(2)当时,函数有最大值11,则的值为_____________.
三、(本大题共2小题,每小题8分,满分16分)
15.如图,已知,证明:.
16.已知一次函数的图象与正比例函数的图象平行且经过点,求该一次函数的表达式.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,在平面直角坐标系中,点和点的坐标分别为.
(1)将向右平移4个单位,再向下平移2个单位,得到,画出;
(2)用无刻度直尺在网格内画出,使得,并写出点的坐标.
18.如图,在和中,点和点分别是和上的点,与交于点,已知.
(1)证明:;
(2)若,求的度数.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在中,于点,点是上一点,连接并延长交于点,已知.
(1)证明:;
(2)若,求的面积.
20.某种中性笔在甲、乙两家文具店的标价都是4元/支,在“双11”期间,两家文具店都进行了优惠活动.甲文具店:购买不超过20支按原价销售,超出20支的部分按6折销售;乙文具店:不论买多少,全部按八折销售.
(1)分别写出甲、乙两家文具店购买这种中性笔所付总费用(元)与购买支数之间的函数表达式;
(2)若某学校购买50枝这种中性笔,请你通过计算说明在哪家文具店购买划算.
六、(本题满分12分)
21.如图,在中,于点平分交于点.
图1 图2
(1)若,如图1,求的度数;
(2)若,如图2,证明:.
七、(本题满分12分)
22.如图,直线与直线交于点,直线与轴、轴分别交于点.
(1)求的值;
(2)直接写出不等式组的解集:_____________;
(3)点是直线上一点,且满足,求点的坐标.
八、(本题满分14分)
23.如图,在中,,点和点分别落在轴的正半轴和轴的正半轴上,已知点的坐标为.
图1 图2 图3
(1)如图1,过点作轴于点,证明:,并直接写出点的坐标;
(2)如图2,若与轴交于点,证明:是的中线;
(3)如图3,若与轴交于点,连接,探索线段和之间的数量关系,并加以证明.
八年级数学参考答案及评分标准
(沪科版)
一、选择题(本大题共10小题,每小题4分,满分40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D C C B D A C B
10.B 如图,过点作于点,,,又,,,,又,,故选项A、C、D正确,而与不一定相等,故选B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果两个三角形是全等三角形,那么它们的对应高线相等
12.3 13.6
14.(1)2(2)1或
(1)把点代入一次函数的表达式中,得,解得;
(2)当时,随增大而增大,则当时,有最大值,,解得;当时,随增大而减小,则当时,有最大值,,解得.综上所述,的值为1或.
三、(本大题共2小题,每小题8分,满分16分)
15.证明:连接,如图.
.
16.解:由题意可设该一次函数的表达式为,
代入点,得,解得,
该一次函数的表达式为.
四、(本大题共2小题,每小题8分,满分16分)
17.解:(1)如图所示;
(2)如图所示,
点.
18.解:(1)证明:在和中,
,
,
,即;
(2)由(1)可知,
.
五、(本大题共2小题,每小题10分,满分20分)
19.(1)证明:.
在和中,,
,
,又,即;
(2),又,
.
20.解:(1)甲文具店:;
乙文具店:.
(2)当时,(元),
(元),
,
当购买50支这种中性笔时,选择在甲文具店购买划算.
六、(本题满分12分)
21.解:(1)在中,.
平分.
,
;
(2).在中,,
,解得,则,
.
在和中,.
22.解:(1)把点代入,得,解得.2分把点和点代入,得,解得,即和的值分别为;
(2);
(3)当时,,解得,即.
由点的坐标,得.
设点的坐标为,则.
由,得,整理,得,
或,解得或.
当时,;当时,,
点的坐标为或.
八、(本题满分14分)
23.(1)证明:由题意可知,
.
又.
点的坐标为;
(2)如图,过点作轴于点,则.
由(1)可知,
,即点是的中点,是的中线;
(3),理由如下:
如图,在上截取,使得,连接.
在和中,,
,则.
由(2)可知,
.
同课章节目录
