19.9勾股定理(第4课时)(教学课件)-2023-2024学年八年级数学上册同步精品课堂(沪教版)
文档属性
| 名称 | 19.9勾股定理(第4课时)(教学课件)-2023-2024学年八年级数学上册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 17:19:45 | ||
图片预览








文档简介
(共26张PPT)
沪教版八年级上册
第 19 章 几何证明
19.9勾股定理(第4课时)
学习目标
1.熟练运用勾股定理和逆定理解决问题。
2.通过复习勾股定理和逆定理的相关内容,总结常用的数学思想方法。
a2+b2=c2
数
a2+b2=c2
三角形三边a、b、c
直角三角形
直角边a、b,斜边c
直角三角形
直角三角形的两直角边为a ,b , 斜边为 c ,则有
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.
勾股定理的逆定理:
a2+ b2=c2
知识梳理
勾股定理:
形
核心内容归纳
基本思想与方法:
数形结合思想,分类讨论思想,方程思想,(转化)化归思想,由特殊到一般(发现——猜想——证明),整体思想、数学建模思想等.
基本经验:
已知三角形两边求第三边,通常利用勾股定理直接计算或者列方程求解,立体图形中的勾股定理问题通常转化为平面图形来解决.
勾股定理的逆定理
勾股定理的逆定理:如果三角形的三边长分别为a,b,c,并且满足a2+b2=c2,那么这个三角形是________三角形.
勾股数:能构成直角三角形的三条边长的三个正整数,称为勾股数.
勾股定理逆定理的应用:
(1)判断三角形的形状;
(2)证明两条线段垂直;
(3)实际应用.
直角
例题7如图19-64,在ABC中,AB=10,BC=24,AC=26,M是AC的中点,求:
(1)B、M两点的距离;
(2)点B到AC的距离.
分析已知△ABC的三边长,可以判断这个三角形是否是直角三角形.常用的方法是运用勾股定理的逆定理.如果它是直角三角形,那么本题就转化为我们熟悉的“求直角三角形斜边上的中线长”和“求直角三角形的直角顶点到斜边的距离”那样的问题.
解:在△ABC中,
∵AB=10,BC=24,AC=26(已知),
例题7如图19-64,在ABC中,AB=10,BC=24,AC=26,M是AC的中点,求:
(1)B、M两点的距离;
(2)点B到AC的距离.
例题7如图19-64,在ABC中,AB=10,BC=24,AC=26,M是AC的中点,求:
(1)B、M两点的距离;
(2)点B到AC的距离.
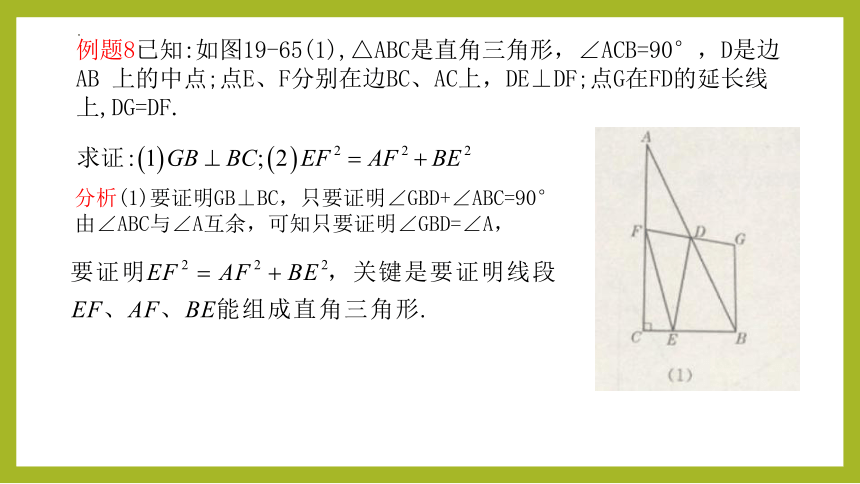
分析(1)要证明GB⊥BC,只要证明∠GBD+∠ABC=90°由∠ABC与∠A互余,可知只要证明∠GBD=∠A,
例题8已知:如图19-65(1),△ABC是直角三角形,∠ACB=90°,D是边AB 上的中点;点E、F分别在边BC、AC上,DE⊥DF;点G在FD的延长线上,DG=DF.
∴△GDB≌△FDA(S.A.S).
得∠GBD=∠A(全等三角形的对应角相等)
∵∠C=90°(已知),
∴∠A+∠ABC=90°(直角三角形的两个锐角余).
得∠GBD+∠ABC=90°(等量代换),
即∠GBC=90°(等量代换),
∴GB⊥BC
例题8已知:如图19-65(1),△ABC是直角三角形,∠ACB=90°,D是边AB 上的中点;点E、F分别在边BC、AC上,DE⊥DF;点G在FD的延长线上,DG=DF.
(2)联结EG(如图19-65(2)).在Rt△GBE中,
例题8已知:如图19-65(1),△ABC是直角三角形,∠ACB=90°,D是边AB 上的中点;点E、F分别在边BC、AC上,DE⊥DF;点G在FD的延长线上,DG=DF.
∴EF=EG(线段垂直平分线上的点到线段两端的距离相等
又由△GDB≌△FDA,得 BG=AF(全等三角形的对应边相等),
1.如图,在△ABC中,D 是边 BC 上的一点,AB=15,AC=13,AD=12,CD=5.
求BC 的长。
课本练习
2如图,公路上 A、B两站相距 25 千米,C、D为两村庄,DA⊥AB,CB⊥AB,垂足分别为点A、B.已知 DA长 10 千米,CB长 15 千米,现要在公路AB 上建一个日用品大卖场E,使得 C、D两村到大卖场E 的距离相等,那么大卖场 E应建在离A 站多远处
1. [2022·河北保定定州市期末]如图是由边长为1的小正方形组成的网格,点A,B,C,D都在格点(小正方形的顶点)上.
(1)求四边形ABCD的周长.
(1)解:由题意可知,AB==3,AD==5,CD==,BC==,
∴四边形ABCD的周长为AB+BC+CD+AD=3+++5=8+2.
(第1题图)
随堂检测
(第3题答图)
(2)求证:∠BCD=90°.
(2)证明:如答图,连接BD.
∵BD==2,CD=,BC=,
∴BC2+CD2=BD2,
∴∠BCD=90°.
(第1题答图)
2 .如图,甲、乙两船从港口A同时出发,甲船以30 n mile/h的速度向北偏东35°方向匀速航行,乙船以40 n mile/h的速度向另一方向匀速航行,2 h后,甲船到达C岛,乙船到达B岛.若C,B两岛相距100 n mile,则乙船航行的角度是南偏东多少度?
(第2题图)
解:在△ABC中,∵AC=2×30=60(n mile),AB=2×40=80(n mile),
∴AC2+AB2=602+802=10 000.
∵BC2=1002=10 000,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,且∠CAB=90°,
∴∠BAD=180°-35°-90°=55°.
故乙船航行的角度是南偏东55°.
(第2题图)
3 .[2022·河南信阳期末]如图,在四边形ABCD中,∠A=90°,AB=3,BC=12,CD=13,DA=4.
(1) (2)
(第3题图)
(1)求四边形ABCD的面积;
(2)如图(2),以A为坐标原点,分别以AB,AD所在直线为x轴、y轴建立平面直角坐标系,点P在y轴上.若=,求点P的坐标.
解:(1)∵∠A=90°,AB=3,DA=4,
∴BD===5.
∵BC=12,CD=13,
∴BD2+BC2=52+122=169,CD2=132=169,
∴BD2+BC2=CD2,
∴△BDC是直角三角形,∠DBC=90°.
∴S四边形ABCD=S△ABD+S△DBC
=AD·AB+DB·BC=×4×3+×5×12=36,
∴四边形ABCD的面积为36.
(1)
(第3题图)
(2)设点P的坐标为(0,a).
∵DA=4,∴D(0,4),
∴PD=|a-4|.
∵S△PBD=S四边形ABCD,
∴PD·AB=×36,
即|a-4|×3=9,得|a-4|=6,
∴a-4=6或a-4=-6,
(2)
(第3题图)
解得a=10或a=-2,
∴点P的坐标为(0,10)或(0,-2).
4. [2022·四川成都彭州期中]森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向AB,由点A飞向点B,已知点C为其中一个着火点,且点C与直线AB上两点A,B的距离分别为600 m和800 m,AB=1 000 m,飞机中心周围500 m以内可以受到洒水影响.
(1)着火点C受洒水影响吗?请说明理由.
(第4题图)
解:(1)着火点C受洒水影响.
理由:如答图,过点C作CD⊥AB于点D.
由题意知,AC=600 m,BC=800 m,AB=1 000 m.
∵AC2+BC2=6002+8002=1 0002,AB2=1 0002,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
∴S△ABC=AC·BC=CD·AB,
∴600×800=1 000CD,∴CD=480 m.
∵飞机中心周围500 m以内可以受到洒水影响,
∴着火点C受洒水影响.
(第10题答图)
(第4题答图)
(2)若飞机的速度为10 m/s,要想扑灭着火点C估计需要13 s,请你通过计算判断着火点C能否被扑灭?
解:(2)如答图,当EC=FC=500 m时,飞机正好喷到着火点C.
∵在Rt△CDE中,
ED===140(m),
∴EF=280 m.
∵飞机的速度为10 m/s,
∴280÷10=28(s).
∵28>13,
∴着火点C能被扑灭.
(第10题答图)
(第4题答图)
5. 新题型 阅读理解题 在△ABC中,BC=a,AC=b,AB=c,如图(1),若∠C=90°,则a2+b2=c2.若△ABC为锐角三角形,小明猜想:a2+b2>c2.证明如下:如图(2),过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,由勾股定理,得AD2=b2-x2.在Rt△ADB中,由勾股定理,得AD2=c2-(a-x)2,∴b2-x2=c2-(a-x)2,∴a2+b2=c2+2ax.∵a>0,x>0,∴2ax>0,∴a2+b2>c2,即当△ABC为锐角三角形时,a2+b2>c2.故小明的猜想是正确的.
(第5题图)
(1)请你猜想,如图(3),当△ABC为钝角三角形时,a2+b2与c2的大小关系;
(2)说明你猜想的结论是否正确〔温馨提示:在图(3)中,作BC边上的高〕.
(2)如答图,过点A作AD⊥BC交BC的延长线于点D,设CD=x.
在Rt△ADC中,由勾股定理,得AD2=b2-x2.
在Rt△ADB中,由勾股定理,得AD2=c2-(a+x)2.
∴b2-x2=c2-(a+x)2,∴a2+b2=c2-2ax.
∵a>0,x>0,∴2ax>0,∴a2+b2<c2.
故当△ABC为钝角三角形时,a2+b2<c2.
(第11题答图)
(第5题答图)
解:(1)当△ABC为钝角三角形时,a2+b2与c2 的大小关系为a2+b2<c2.
方 法
认真审题,画出符合题意的图 形,熟练运用勾股定理及其逆定理来解决问题。
勾股定理及逆
定理的应用
解决不规则图形面积以及综合性的实际问题.
应 用
三角形的边长,周长,面积及三角形形状问题
思想
数形结合思想,分类讨论思想,方程思想,(转化)化归思想,由特殊到一般(发现——猜想——证明),整体思想、数学建模思想
课堂小结
沪教版八年级上册
第 19 章 几何证明
19.9勾股定理(第4课时)
学习目标
1.熟练运用勾股定理和逆定理解决问题。
2.通过复习勾股定理和逆定理的相关内容,总结常用的数学思想方法。
a2+b2=c2
数
a2+b2=c2
三角形三边a、b、c
直角三角形
直角边a、b,斜边c
直角三角形
直角三角形的两直角边为a ,b , 斜边为 c ,则有
三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.
勾股定理的逆定理:
a2+ b2=c2
知识梳理
勾股定理:
形
核心内容归纳
基本思想与方法:
数形结合思想,分类讨论思想,方程思想,(转化)化归思想,由特殊到一般(发现——猜想——证明),整体思想、数学建模思想等.
基本经验:
已知三角形两边求第三边,通常利用勾股定理直接计算或者列方程求解,立体图形中的勾股定理问题通常转化为平面图形来解决.
勾股定理的逆定理
勾股定理的逆定理:如果三角形的三边长分别为a,b,c,并且满足a2+b2=c2,那么这个三角形是________三角形.
勾股数:能构成直角三角形的三条边长的三个正整数,称为勾股数.
勾股定理逆定理的应用:
(1)判断三角形的形状;
(2)证明两条线段垂直;
(3)实际应用.
直角
例题7如图19-64,在ABC中,AB=10,BC=24,AC=26,M是AC的中点,求:
(1)B、M两点的距离;
(2)点B到AC的距离.
分析已知△ABC的三边长,可以判断这个三角形是否是直角三角形.常用的方法是运用勾股定理的逆定理.如果它是直角三角形,那么本题就转化为我们熟悉的“求直角三角形斜边上的中线长”和“求直角三角形的直角顶点到斜边的距离”那样的问题.
解:在△ABC中,
∵AB=10,BC=24,AC=26(已知),
例题7如图19-64,在ABC中,AB=10,BC=24,AC=26,M是AC的中点,求:
(1)B、M两点的距离;
(2)点B到AC的距离.
例题7如图19-64,在ABC中,AB=10,BC=24,AC=26,M是AC的中点,求:
(1)B、M两点的距离;
(2)点B到AC的距离.
分析(1)要证明GB⊥BC,只要证明∠GBD+∠ABC=90°由∠ABC与∠A互余,可知只要证明∠GBD=∠A,
例题8已知:如图19-65(1),△ABC是直角三角形,∠ACB=90°,D是边AB 上的中点;点E、F分别在边BC、AC上,DE⊥DF;点G在FD的延长线上,DG=DF.
∴△GDB≌△FDA(S.A.S).
得∠GBD=∠A(全等三角形的对应角相等)
∵∠C=90°(已知),
∴∠A+∠ABC=90°(直角三角形的两个锐角余).
得∠GBD+∠ABC=90°(等量代换),
即∠GBC=90°(等量代换),
∴GB⊥BC
例题8已知:如图19-65(1),△ABC是直角三角形,∠ACB=90°,D是边AB 上的中点;点E、F分别在边BC、AC上,DE⊥DF;点G在FD的延长线上,DG=DF.
(2)联结EG(如图19-65(2)).在Rt△GBE中,
例题8已知:如图19-65(1),△ABC是直角三角形,∠ACB=90°,D是边AB 上的中点;点E、F分别在边BC、AC上,DE⊥DF;点G在FD的延长线上,DG=DF.
∴EF=EG(线段垂直平分线上的点到线段两端的距离相等
又由△GDB≌△FDA,得 BG=AF(全等三角形的对应边相等),
1.如图,在△ABC中,D 是边 BC 上的一点,AB=15,AC=13,AD=12,CD=5.
求BC 的长。
课本练习
2如图,公路上 A、B两站相距 25 千米,C、D为两村庄,DA⊥AB,CB⊥AB,垂足分别为点A、B.已知 DA长 10 千米,CB长 15 千米,现要在公路AB 上建一个日用品大卖场E,使得 C、D两村到大卖场E 的距离相等,那么大卖场 E应建在离A 站多远处
1. [2022·河北保定定州市期末]如图是由边长为1的小正方形组成的网格,点A,B,C,D都在格点(小正方形的顶点)上.
(1)求四边形ABCD的周长.
(1)解:由题意可知,AB==3,AD==5,CD==,BC==,
∴四边形ABCD的周长为AB+BC+CD+AD=3+++5=8+2.
(第1题图)
随堂检测
(第3题答图)
(2)求证:∠BCD=90°.
(2)证明:如答图,连接BD.
∵BD==2,CD=,BC=,
∴BC2+CD2=BD2,
∴∠BCD=90°.
(第1题答图)
2 .如图,甲、乙两船从港口A同时出发,甲船以30 n mile/h的速度向北偏东35°方向匀速航行,乙船以40 n mile/h的速度向另一方向匀速航行,2 h后,甲船到达C岛,乙船到达B岛.若C,B两岛相距100 n mile,则乙船航行的角度是南偏东多少度?
(第2题图)
解:在△ABC中,∵AC=2×30=60(n mile),AB=2×40=80(n mile),
∴AC2+AB2=602+802=10 000.
∵BC2=1002=10 000,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,且∠CAB=90°,
∴∠BAD=180°-35°-90°=55°.
故乙船航行的角度是南偏东55°.
(第2题图)
3 .[2022·河南信阳期末]如图,在四边形ABCD中,∠A=90°,AB=3,BC=12,CD=13,DA=4.
(1) (2)
(第3题图)
(1)求四边形ABCD的面积;
(2)如图(2),以A为坐标原点,分别以AB,AD所在直线为x轴、y轴建立平面直角坐标系,点P在y轴上.若=,求点P的坐标.
解:(1)∵∠A=90°,AB=3,DA=4,
∴BD===5.
∵BC=12,CD=13,
∴BD2+BC2=52+122=169,CD2=132=169,
∴BD2+BC2=CD2,
∴△BDC是直角三角形,∠DBC=90°.
∴S四边形ABCD=S△ABD+S△DBC
=AD·AB+DB·BC=×4×3+×5×12=36,
∴四边形ABCD的面积为36.
(1)
(第3题图)
(2)设点P的坐标为(0,a).
∵DA=4,∴D(0,4),
∴PD=|a-4|.
∵S△PBD=S四边形ABCD,
∴PD·AB=×36,
即|a-4|×3=9,得|a-4|=6,
∴a-4=6或a-4=-6,
(2)
(第3题图)
解得a=10或a=-2,
∴点P的坐标为(0,10)或(0,-2).
4. [2022·四川成都彭州期中]森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向AB,由点A飞向点B,已知点C为其中一个着火点,且点C与直线AB上两点A,B的距离分别为600 m和800 m,AB=1 000 m,飞机中心周围500 m以内可以受到洒水影响.
(1)着火点C受洒水影响吗?请说明理由.
(第4题图)
解:(1)着火点C受洒水影响.
理由:如答图,过点C作CD⊥AB于点D.
由题意知,AC=600 m,BC=800 m,AB=1 000 m.
∵AC2+BC2=6002+8002=1 0002,AB2=1 0002,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.
∴S△ABC=AC·BC=CD·AB,
∴600×800=1 000CD,∴CD=480 m.
∵飞机中心周围500 m以内可以受到洒水影响,
∴着火点C受洒水影响.
(第10题答图)
(第4题答图)
(2)若飞机的速度为10 m/s,要想扑灭着火点C估计需要13 s,请你通过计算判断着火点C能否被扑灭?
解:(2)如答图,当EC=FC=500 m时,飞机正好喷到着火点C.
∵在Rt△CDE中,
ED===140(m),
∴EF=280 m.
∵飞机的速度为10 m/s,
∴280÷10=28(s).
∵28>13,
∴着火点C能被扑灭.
(第10题答图)
(第4题答图)
5. 新题型 阅读理解题 在△ABC中,BC=a,AC=b,AB=c,如图(1),若∠C=90°,则a2+b2=c2.若△ABC为锐角三角形,小明猜想:a2+b2>c2.证明如下:如图(2),过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,由勾股定理,得AD2=b2-x2.在Rt△ADB中,由勾股定理,得AD2=c2-(a-x)2,∴b2-x2=c2-(a-x)2,∴a2+b2=c2+2ax.∵a>0,x>0,∴2ax>0,∴a2+b2>c2,即当△ABC为锐角三角形时,a2+b2>c2.故小明的猜想是正确的.
(第5题图)
(1)请你猜想,如图(3),当△ABC为钝角三角形时,a2+b2与c2的大小关系;
(2)说明你猜想的结论是否正确〔温馨提示:在图(3)中,作BC边上的高〕.
(2)如答图,过点A作AD⊥BC交BC的延长线于点D,设CD=x.
在Rt△ADC中,由勾股定理,得AD2=b2-x2.
在Rt△ADB中,由勾股定理,得AD2=c2-(a+x)2.
∴b2-x2=c2-(a+x)2,∴a2+b2=c2-2ax.
∵a>0,x>0,∴2ax>0,∴a2+b2<c2.
故当△ABC为钝角三角形时,a2+b2<c2.
(第11题答图)
(第5题答图)
解:(1)当△ABC为钝角三角形时,a2+b2与c2 的大小关系为a2+b2<c2.
方 法
认真审题,画出符合题意的图 形,熟练运用勾股定理及其逆定理来解决问题。
勾股定理及逆
定理的应用
解决不规则图形面积以及综合性的实际问题.
应 用
三角形的边长,周长,面积及三角形形状问题
思想
数形结合思想,分类讨论思想,方程思想,(转化)化归思想,由特殊到一般(发现——猜想——证明),整体思想、数学建模思想
课堂小结
