15.2.1.2分式的乘方 课件(共22张PPT)
文档属性
| 名称 | 15.2.1.2分式的乘方 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 38.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-21 17:06:47 | ||
图片预览




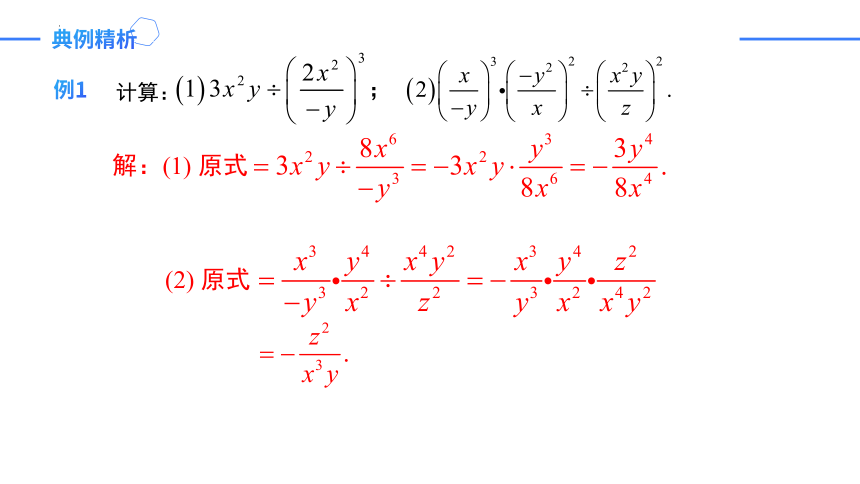
文档简介
(共22张PPT)
第15章
分式
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
15.2.1.2
分式的乘方
情景引入
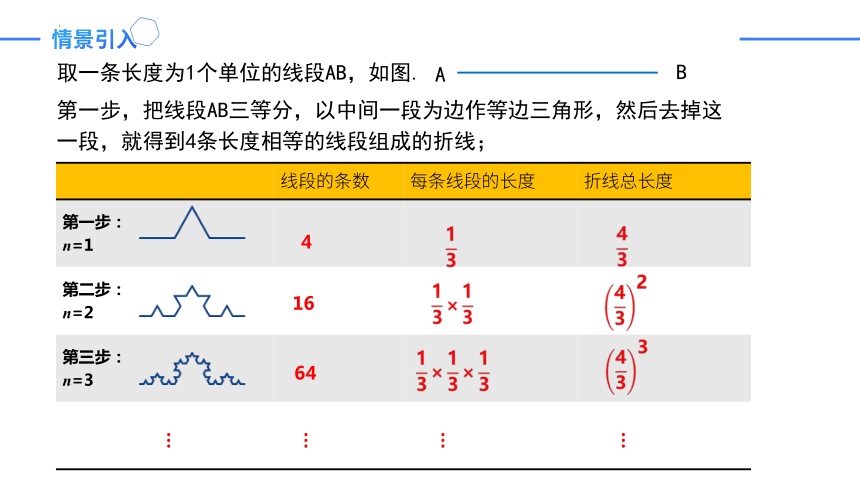
取一条长度为1个单位的线段AB,如图.
第一步,把线段AB三等分,以中间一段为边作等边三角形,然后去掉这一段,就得到4条长度相等的线段组成的折线;
A
B
线段的条数 每条线段的长度 折线总长度
第一步: n=1
第二步: n=2
第三步: n=3
4
16
64
…
…
…
…
新知探究
思考:
计算:
由乘方的意义和分数乘法的法则,可得
n个
n个
n个
新知探究
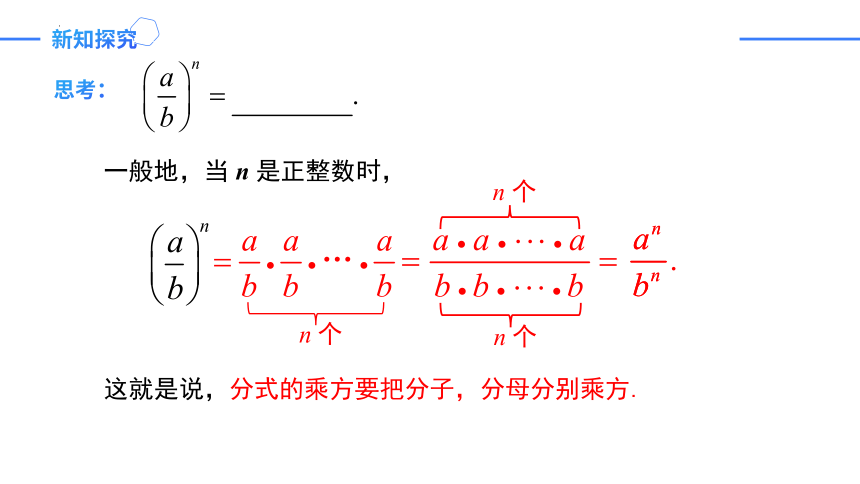
思考:
一般地,当 n 是正整数时,
n 个
n 个
n 个
这就是说,分式的乘方要把分子,分母分别乘方.
新知探究
分式的乘方法则
分式乘方时,一定要把分子、分母同时分别乘方,不要把 写成 .
×
√
(1) 同底数的幂相乘:am·an =am+n ;
(2) 同底数的幂相除:am÷an=am-n;
(3) 幂的乘方: (am)n=amn;
(4) 积的乘方: (ab)n=anbn;
(5) 分式的乘方:
正整数指数幂的运算法则
典例精析
例1
计算:
解:(1) 原式
(2) 原式
典例精析
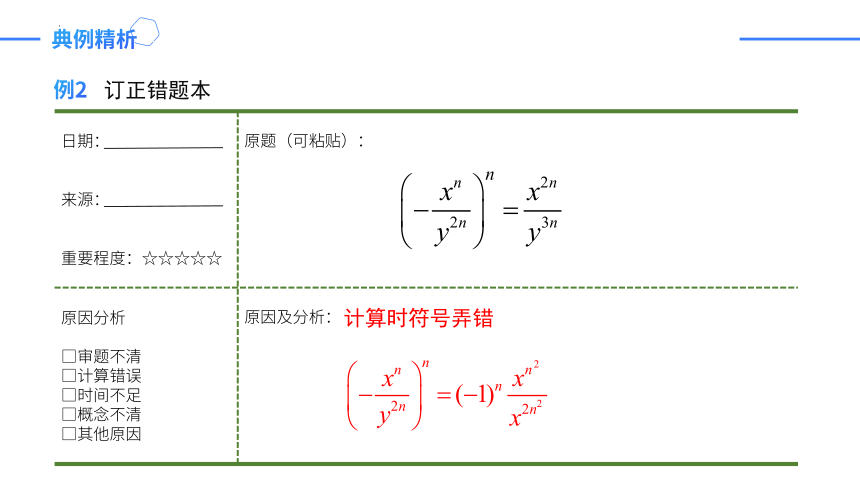
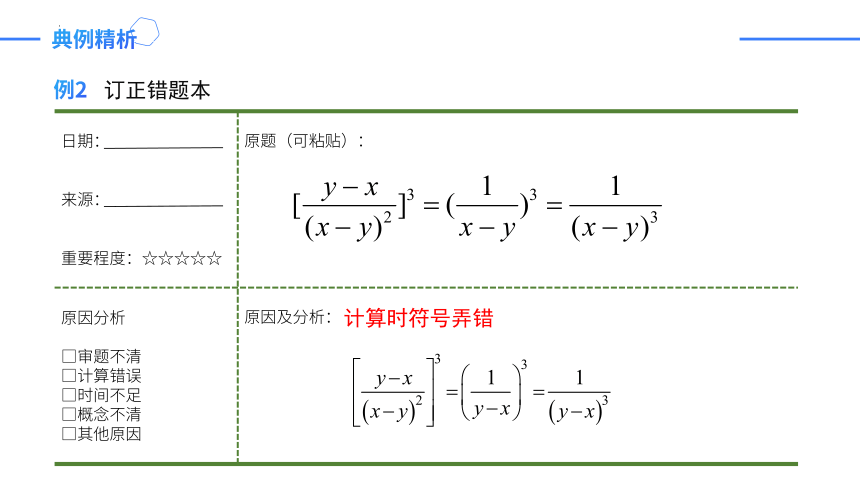
例2
日期: 原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析 □审题不清 □计算错误 □时间不足 □概念不清 □其他原因 原因及分析:
订正错题本
计算时符号弄错
典例精析
例2
日期: 原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析 □审题不清 □计算错误 □时间不足 □概念不清 □其他原因 原因及分析:
订正错题本
计算时符号弄错
典例精析
例3
解:
典例精析
归纳总结
进行分式的乘除、乘方混合运算时,要严格按照运算顺序进行运算,先算乘方,再算乘除. 注意结果一定要化成一个整式或最简分式的形式.
典例精析
例4
=(a-2)(a+1)=a2-a-2.
(2)
(2)原式 =
典例精析
01
步骤01
先把除法统一成乘法运算;
02
步骤02
分子、分母中能分解因式的多项式分解因式;
04
步骤04
结果应是最简分式或整式.
03
步骤03
确定分式的符号,然后约分;
分式乘除混合运算的一般步骤
典例精析
例5
日期: 原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析 □审题不清 □计算错误 □时间不足 □概念不清 □其他原因 原因及分析:
订正错题本
典例精析
① 按照运算法则运算;
② 乘除运算属于同级运算,应按照从左到右的原则,
不能交换运算顺序;
③ 当除写成乘的形式时,灵活的应用乘法交换律和
结合律可起到简化运算的作用;
④ 结果必须化成最简分式或整式的形式.
典例精析
例6
化简求值:
典例精析
引例
购买西瓜时,西瓜瓤占整个西瓜的比例越大越好.假如我们把西瓜都看成球形,并把西瓜瓤的密度看成是均匀的,你认为买大西瓜合算还是买小西瓜合算
R越大, 越 , 越 , 越 ,
小
大
越大
大
所以,买大西瓜较划算
归纳总结
分式乘除混合运算
乘方运算
注意
(1) 乘除运算属于同级运算,应按照先出现的先算的原则,不能交换运算顺序
乘方法则
(2) 当除变成乘的形式时,灵活运用乘法交换律和结合律可以简化运算
混合运算
乘除法运算及乘方法则
先算乘方,再算乘除
当堂检测
C
B
D
当堂检测
5.计算:
4.填空
﹣2a2b
3c
=
(
)
2
4a4b2
9c2
(2)
﹣xy2
3z
=
(
)
4
x4y8
81z4
(3)
3yz
5x2
=
(
)
3
27y3z3
125x6
当堂检测
6.计算:
解:原式 =
解:原式 =
当堂检测
7. 计算:
解:原式
第15章
分式
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
15.2.1.2
分式的乘方
情景引入
取一条长度为1个单位的线段AB,如图.
第一步,把线段AB三等分,以中间一段为边作等边三角形,然后去掉这一段,就得到4条长度相等的线段组成的折线;
A
B
线段的条数 每条线段的长度 折线总长度
第一步: n=1
第二步: n=2
第三步: n=3
4
16
64
…
…
…
…
新知探究
思考:
计算:
由乘方的意义和分数乘法的法则,可得
n个
n个
n个
新知探究
思考:
一般地,当 n 是正整数时,
n 个
n 个
n 个
这就是说,分式的乘方要把分子,分母分别乘方.
新知探究
分式的乘方法则
分式乘方时,一定要把分子、分母同时分别乘方,不要把 写成 .
×
√
(1) 同底数的幂相乘:am·an =am+n ;
(2) 同底数的幂相除:am÷an=am-n;
(3) 幂的乘方: (am)n=amn;
(4) 积的乘方: (ab)n=anbn;
(5) 分式的乘方:
正整数指数幂的运算法则
典例精析
例1
计算:
解:(1) 原式
(2) 原式
典例精析
例2
日期: 原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析 □审题不清 □计算错误 □时间不足 □概念不清 □其他原因 原因及分析:
订正错题本
计算时符号弄错
典例精析
例2
日期: 原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析 □审题不清 □计算错误 □时间不足 □概念不清 □其他原因 原因及分析:
订正错题本
计算时符号弄错
典例精析
例3
解:
典例精析
归纳总结
进行分式的乘除、乘方混合运算时,要严格按照运算顺序进行运算,先算乘方,再算乘除. 注意结果一定要化成一个整式或最简分式的形式.
典例精析
例4
=(a-2)(a+1)=a2-a-2.
(2)
(2)原式 =
典例精析
01
步骤01
先把除法统一成乘法运算;
02
步骤02
分子、分母中能分解因式的多项式分解因式;
04
步骤04
结果应是最简分式或整式.
03
步骤03
确定分式的符号,然后约分;
分式乘除混合运算的一般步骤
典例精析
例5
日期: 原题(可粘贴):
来源:
重要程度:☆☆☆☆☆
原因分析 □审题不清 □计算错误 □时间不足 □概念不清 □其他原因 原因及分析:
订正错题本
典例精析
① 按照运算法则运算;
② 乘除运算属于同级运算,应按照从左到右的原则,
不能交换运算顺序;
③ 当除写成乘的形式时,灵活的应用乘法交换律和
结合律可起到简化运算的作用;
④ 结果必须化成最简分式或整式的形式.
典例精析
例6
化简求值:
典例精析
引例
购买西瓜时,西瓜瓤占整个西瓜的比例越大越好.假如我们把西瓜都看成球形,并把西瓜瓤的密度看成是均匀的,你认为买大西瓜合算还是买小西瓜合算
R越大, 越 , 越 , 越 ,
小
大
越大
大
所以,买大西瓜较划算
归纳总结
分式乘除混合运算
乘方运算
注意
(1) 乘除运算属于同级运算,应按照先出现的先算的原则,不能交换运算顺序
乘方法则
(2) 当除变成乘的形式时,灵活运用乘法交换律和结合律可以简化运算
混合运算
乘除法运算及乘方法则
先算乘方,再算乘除
当堂检测
C
B
D
当堂检测
5.计算:
4.填空
﹣2a2b
3c
=
(
)
2
4a4b2
9c2
(2)
﹣xy2
3z
=
(
)
4
x4y8
81z4
(3)
3yz
5x2
=
(
)
3
27y3z3
125x6
当堂检测
6.计算:
解:原式 =
解:原式 =
当堂检测
7. 计算:
解:原式
