1.5.1 有理数的乘方 课件 (共22张PPT)人教版七年级数学上册
文档属性
| 名称 | 1.5.1 有理数的乘方 课件 (共22张PPT)人教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-19 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
人教版七年级数学上册
1.5.1+有理数的乘方
1.理解并掌握有理数的乘方、幂、底数、指数的概念及意义.(难点)
2.能够正确进行有理数的乘方运算.(重点)
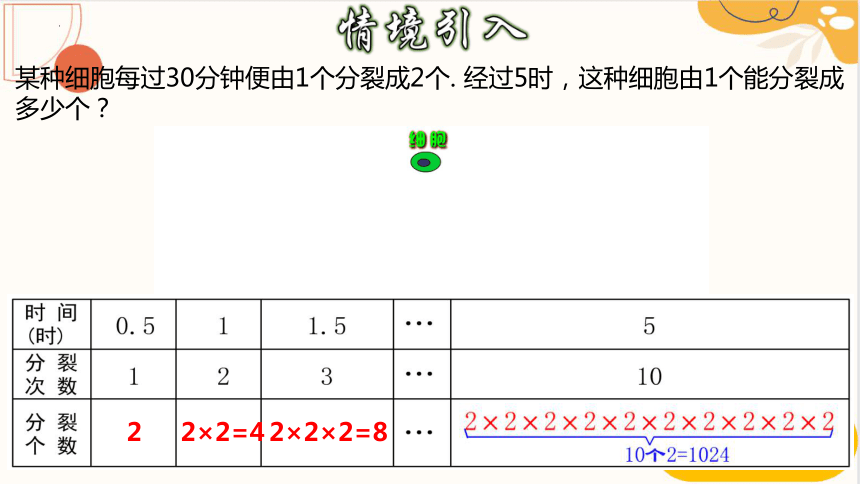
某种细胞每过30分钟便由1个分裂成2个. 经过5时,这种细胞由1个能分裂成多少个?
2
2×2=4
2×2×2=8
边长为2cm的正方形的面积是2×2=4(cm2);棱长为2cm的正方体的体积2×
2×2=8(cm3).
2×2记作22,读作“2的平方”(或“2的二次方”);
2×2×2×2×2×2×2×2×2×2记作_____,读作___________.
2×2×2记作23,读作“2的立方”(或“2的三次方”).
(-2)×(-2)×(-2)×(-2)记作________,读作_____________.
210
2的十次方
(-2)4
-2的四次方
记作________,读作_____________.
-????????的五次方
?
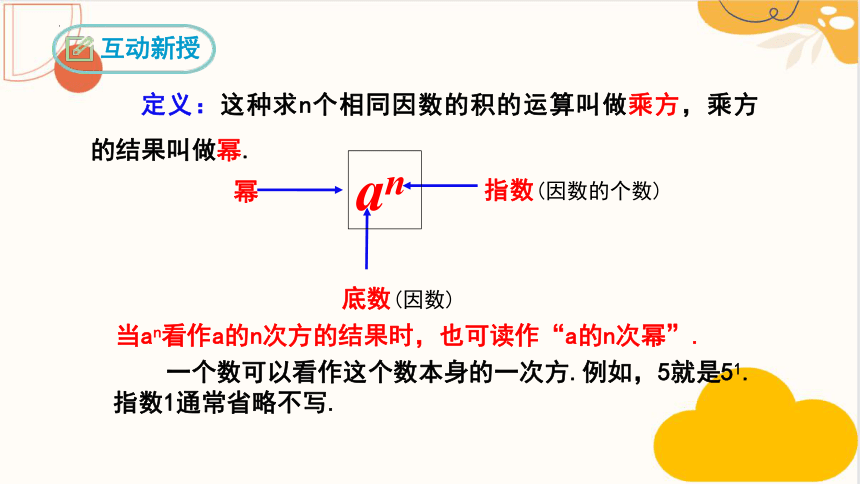
定义:这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
互动新授
幂
指数(因数的个数)
底数(因数)
an
当an看作a的n次方的结果时,也可读作“a的n次幂”.
一个数可以看作这个数本身的一次方.例如,5就是51.指数1通常省略不写.
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a· ·a = an
n个
…
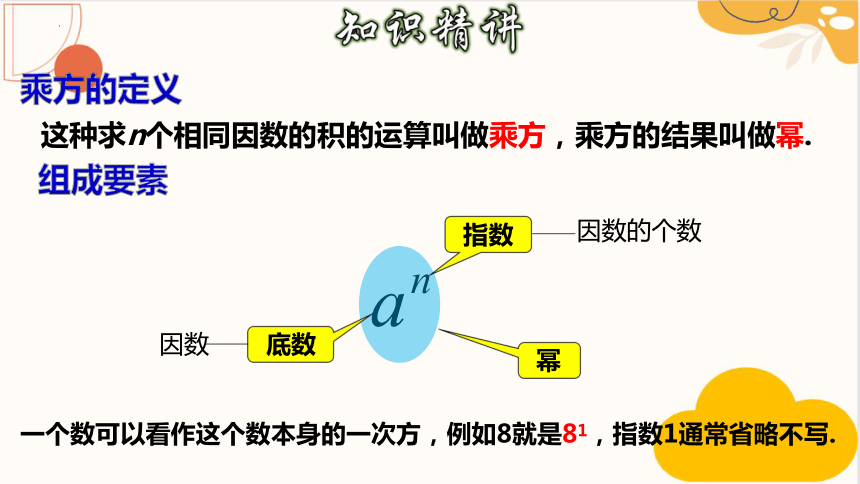
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方,例如8就是81,指数1通常省略不写.
组成要素
幂
指数
底数
因数
因数的个数
乘方的定义
典例精析
例1 计算:
(1)(-4)3; (2) (-2)4; (3) .
(2)(-2)4 =(-2)×(2)×(2)×(2)=16;
(1)(-4)3 =(-4)×(-4)×(-4)=-64;
解:
乘方运算转化为乘法运算.
(1)(-3)2的底数是_____,指数是_____,(-7)3表示2个_____相乘,读作_____的二次方,也读作-7的________.
(2) 表示____个 相乘,读作 的_____次方,也读作 的 次幂,其中 叫做 ,6叫做 .
-7
2
-7
-3
六
6
底数
指数
二次幂
六
互动新授
问题1:从前面的计算中你能发现什么规律?
当指数是____数时,负数的幂是_____数;
(-4)3=(-4)×(-4)×(-4)=-64;
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
当指数是____数时,负数的幂是_____数;
正
奇
负
偶
稍复杂的有理数的混合运算
难点
例2.计算:
(1)-43÷916×(-34)2-(1-32)×2; (2)-14-(2-112)×13×[5+(-2)3];
(3)-24÷[1-(-3)2]+(23-35)×(-15); (4)-32-|(-5)3|×(-25)2-18+|-(-3)2|.
?
解:(1)原式=-64×169×+8×2
=-64+16
=-48;
?
(2)原式=-1-12×13×(5-8)
=-1-12×13×(-3)
=-1+12
=-12;
?
根据有理数乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
正数的任何次幂都是正数,0的任何正整数次幂都是0.
总结归纳
稍复杂的有理数的混合运算
难点
例2.计算:
(1)-43÷916×(-34)2-(1-32)×2; (2)-14-(2-112)×13×[5+(-2)3];
(3)-24÷[1-(-3)2]+(23-35)×(-15); (4)-32-|(-5)3|×(-25)2-18+|-(-3)2|.
?
(3)原式=-16+(1-9)+(-23×15+35×15) =-16÷(-8)+(-10+9)
=2-1
=1;
?
(4)原式=-9-125×425-18÷9
=-9-20-2
=-31.
?
典题精讲
3.观察下列一组算式:32-12=8=8×1,52-32=16=8×2,
72-52=24=8×3,92-72 =32=8×4,….
根据你所发现的规律,猜想2 0152-2 0132=8× .
4.观察下列等式:
1×5+4=32, 2×6+4=42,
3×7+4=52, 4×8+4=62.
请你在观察后用你得出的规律填空:
_________× + =502.
1007
48
52
4
(-2)4与-24一样吗?为什么?
(-2)4表示4个-2相乘,即:(-2)×(-2)×(-2)×(-2)
-24表示4个2相乘的相反数,即:-2×2×2×2
(-2)4与-24互为相反数.
【点睛】负数的乘方,在书写时一定要把整个负数(连同负号)用小括号括起来.
例3.观察下面三行数:
-2, 4, -8, 16, -32, 64,…;①
0, 6, -6, 18, -30, 66,…; ②
-1, 2, -4, 8, -16, 32,…. ③
(1)第①行数按什么规律排列?
解:(1)第①行数是-2,(-2)2,(-2)3,(-2)4,…
分析:观察①,发现各数均为2的倍数.联系数的乘方,从符号和绝对值两方面考虑,可发现排列的规律.
有理数的运算规律问题
难点
典例精析
例4 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
所以(-8)5=-32768,(-3)6=729.
729
与 一样吗?为什么?
【点睛】分数的乘方,在书写时一定要把整个分数(连同负号)用小括号括起来.
表示4个 相乘,即:
表示4个2相乘的 ,即:
与 不相等.
小试牛刀
1.有理数混合运算的顺序是:
(1)先__________,再__________,最后__________;
(2)同级运算,从______到______进行;
(3)如有括号,先做________的运算,按______括号、______括号、______括号依次进行.
乘方
乘除
加减
左
右
括号内
小
中
大
2.计算:-16- ×[5-(-(3)2]=______- ×(5-____)=
________- ×________=________-________=________.
-1
9
-1
(-4)
-1
(-1)
0
小试牛刀
3.观察下面“品”字形中各数之间的规律,根据观察到的规
律得出a的值为( )
A.23 B.75 C.77 D.139
B
4.下列各式计算结果正确的是( )
A.-23-2×6=-60 B.-52× =-1
÷1÷ =235 D.-24×(-(3)2=-144
D
课堂小结
1.有理数的混合运算,除了运用运算法则外,还要灵活使用
运算律,从而简化计算.
2.进行有理数的混合运算时,时常出现“-”或“+”号的
问题.在一个算式中“-”号有两重意义: 一是表示性质,
如负数;二是运算符号,表示减去,所以要根据具体情况
去正确理解.“+”号也是一样.因此在具体运算中要特
别注意区别运算符号与性质符号.
同学们,
下节课见!
人教版七年级数学上册
1.5.1+有理数的乘方
1.理解并掌握有理数的乘方、幂、底数、指数的概念及意义.(难点)
2.能够正确进行有理数的乘方运算.(重点)
某种细胞每过30分钟便由1个分裂成2个. 经过5时,这种细胞由1个能分裂成多少个?
2
2×2=4
2×2×2=8
边长为2cm的正方形的面积是2×2=4(cm2);棱长为2cm的正方体的体积2×
2×2=8(cm3).
2×2记作22,读作“2的平方”(或“2的二次方”);
2×2×2×2×2×2×2×2×2×2记作_____,读作___________.
2×2×2记作23,读作“2的立方”(或“2的三次方”).
(-2)×(-2)×(-2)×(-2)记作________,读作_____________.
210
2的十次方
(-2)4
-2的四次方
记作________,读作_____________.
-????????的五次方
?
定义:这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
互动新授
幂
指数(因数的个数)
底数(因数)
an
当an看作a的n次方的结果时,也可读作“a的n次幂”.
一个数可以看作这个数本身的一次方.例如,5就是51.指数1通常省略不写.
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
a·a·a· ·a = an
n个
…
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方,例如8就是81,指数1通常省略不写.
组成要素
幂
指数
底数
因数
因数的个数
乘方的定义
典例精析
例1 计算:
(1)(-4)3; (2) (-2)4; (3) .
(2)(-2)4 =(-2)×(2)×(2)×(2)=16;
(1)(-4)3 =(-4)×(-4)×(-4)=-64;
解:
乘方运算转化为乘法运算.
(1)(-3)2的底数是_____,指数是_____,(-7)3表示2个_____相乘,读作_____的二次方,也读作-7的________.
(2) 表示____个 相乘,读作 的_____次方,也读作 的 次幂,其中 叫做 ,6叫做 .
-7
2
-7
-3
六
6
底数
指数
二次幂
六
互动新授
问题1:从前面的计算中你能发现什么规律?
当指数是____数时,负数的幂是_____数;
(-4)3=(-4)×(-4)×(-4)=-64;
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
当指数是____数时,负数的幂是_____数;
正
奇
负
偶
稍复杂的有理数的混合运算
难点
例2.计算:
(1)-43÷916×(-34)2-(1-32)×2; (2)-14-(2-112)×13×[5+(-2)3];
(3)-24÷[1-(-3)2]+(23-35)×(-15); (4)-32-|(-5)3|×(-25)2-18+|-(-3)2|.
?
解:(1)原式=-64×169×+8×2
=-64+16
=-48;
?
(2)原式=-1-12×13×(5-8)
=-1-12×13×(-3)
=-1+12
=-12;
?
根据有理数乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
正数的任何次幂都是正数,0的任何正整数次幂都是0.
总结归纳
稍复杂的有理数的混合运算
难点
例2.计算:
(1)-43÷916×(-34)2-(1-32)×2; (2)-14-(2-112)×13×[5+(-2)3];
(3)-24÷[1-(-3)2]+(23-35)×(-15); (4)-32-|(-5)3|×(-25)2-18+|-(-3)2|.
?
(3)原式=-16+(1-9)+(-23×15+35×15) =-16÷(-8)+(-10+9)
=2-1
=1;
?
(4)原式=-9-125×425-18÷9
=-9-20-2
=-31.
?
典题精讲
3.观察下列一组算式:32-12=8=8×1,52-32=16=8×2,
72-52=24=8×3,92-72 =32=8×4,….
根据你所发现的规律,猜想2 0152-2 0132=8× .
4.观察下列等式:
1×5+4=32, 2×6+4=42,
3×7+4=52, 4×8+4=62.
请你在观察后用你得出的规律填空:
_________× + =502.
1007
48
52
4
(-2)4与-24一样吗?为什么?
(-2)4表示4个-2相乘,即:(-2)×(-2)×(-2)×(-2)
-24表示4个2相乘的相反数,即:-2×2×2×2
(-2)4与-24互为相反数.
【点睛】负数的乘方,在书写时一定要把整个负数(连同负号)用小括号括起来.
例3.观察下面三行数:
-2, 4, -8, 16, -32, 64,…;①
0, 6, -6, 18, -30, 66,…; ②
-1, 2, -4, 8, -16, 32,…. ③
(1)第①行数按什么规律排列?
解:(1)第①行数是-2,(-2)2,(-2)3,(-2)4,…
分析:观察①,发现各数均为2的倍数.联系数的乘方,从符号和绝对值两方面考虑,可发现排列的规律.
有理数的运算规律问题
难点
典例精析
例4 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
所以(-8)5=-32768,(-3)6=729.
729
与 一样吗?为什么?
【点睛】分数的乘方,在书写时一定要把整个分数(连同负号)用小括号括起来.
表示4个 相乘,即:
表示4个2相乘的 ,即:
与 不相等.
小试牛刀
1.有理数混合运算的顺序是:
(1)先__________,再__________,最后__________;
(2)同级运算,从______到______进行;
(3)如有括号,先做________的运算,按______括号、______括号、______括号依次进行.
乘方
乘除
加减
左
右
括号内
小
中
大
2.计算:-16- ×[5-(-(3)2]=______- ×(5-____)=
________- ×________=________-________=________.
-1
9
-1
(-4)
-1
(-1)
0
小试牛刀
3.观察下面“品”字形中各数之间的规律,根据观察到的规
律得出a的值为( )
A.23 B.75 C.77 D.139
B
4.下列各式计算结果正确的是( )
A.-23-2×6=-60 B.-52× =-1
÷1÷ =235 D.-24×(-(3)2=-144
D
课堂小结
1.有理数的混合运算,除了运用运算法则外,还要灵活使用
运算律,从而简化计算.
2.进行有理数的混合运算时,时常出现“-”或“+”号的
问题.在一个算式中“-”号有两重意义: 一是表示性质,
如负数;二是运算符号,表示减去,所以要根据具体情况
去正确理解.“+”号也是一样.因此在具体运算中要特
别注意区别运算符号与性质符号.
同学们,
下节课见!
