物理人教版(2019)必修第二册5.2运动的合成与分解(共40张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册5.2运动的合成与分解(共40张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 26.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-12-19 00:00:00 | ||
图片预览






文档简介
(共40张PPT)
新课导入
军事演习过程中投掷物资是在目标上空投放还是在离目标有一段距离时提前投放,为什么?
如何研究这一类运动呢
01
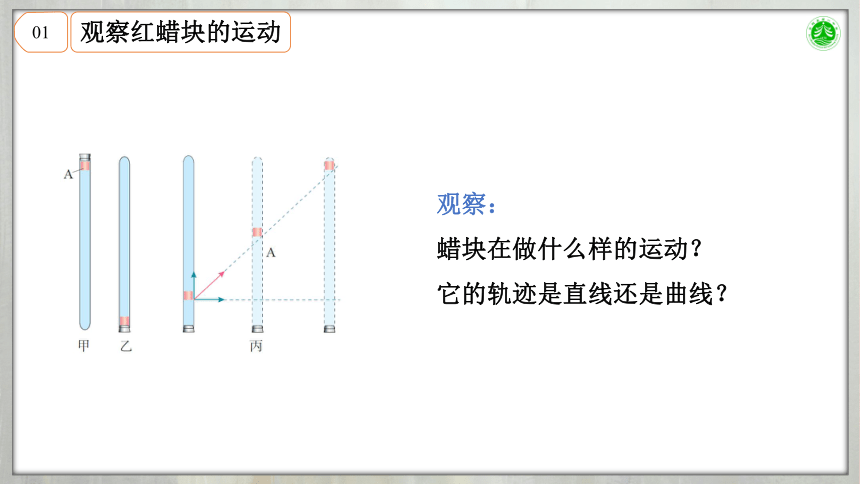
观察红蜡块的运动
观察:
蜡块在做什么样的运动?
它的轨迹是直线还是曲线?
01
观察红蜡块的运动
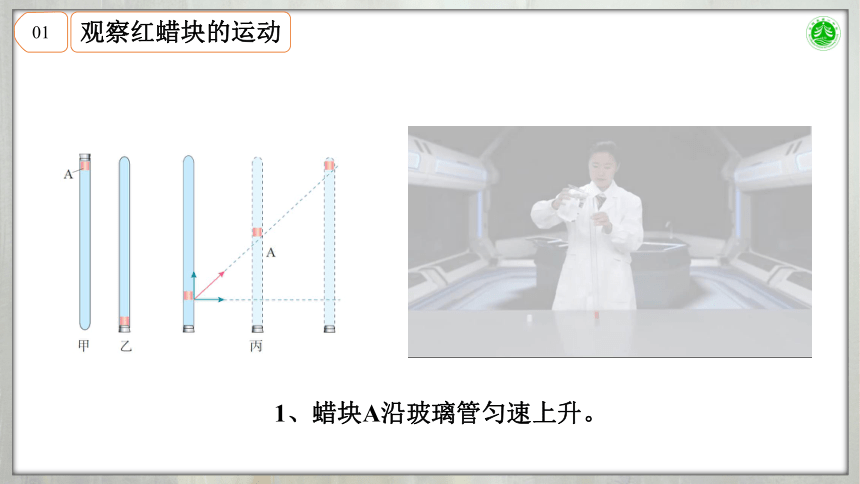
1、蜡块A沿玻璃管匀速上升。
01
观察红蜡块的运动
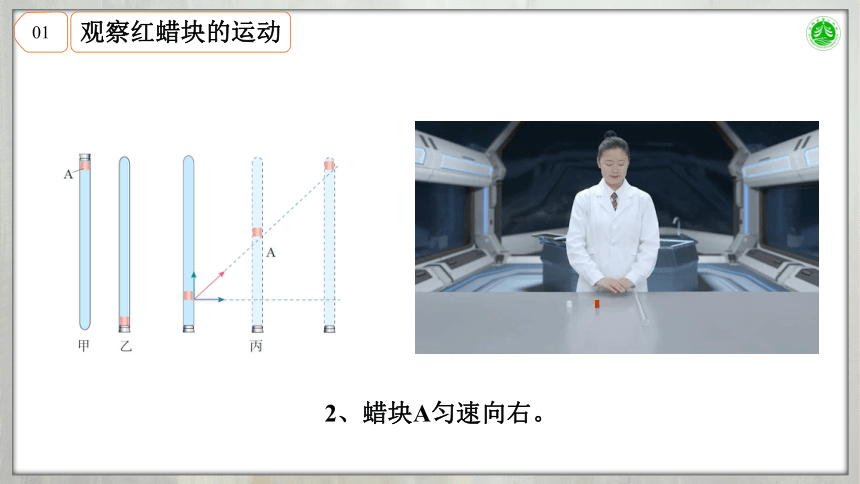
2、蜡块A匀速向右。
01
观察红蜡块的运动
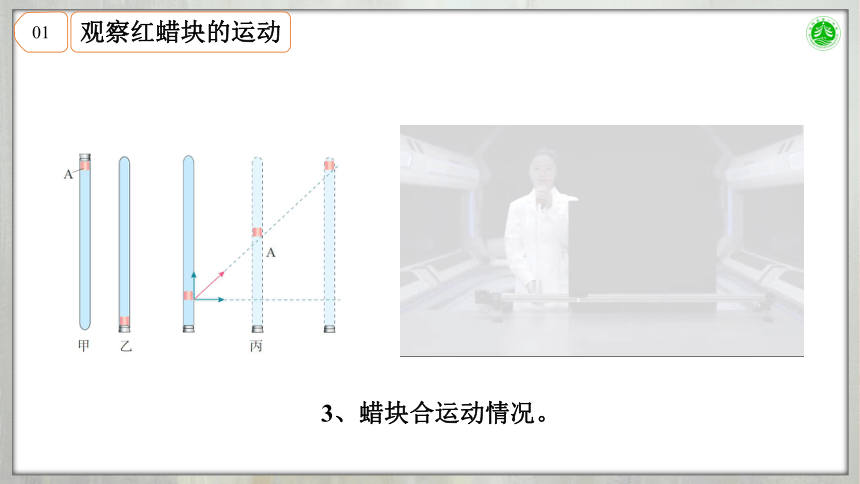
3、蜡块合运动情况。
02
定量研究运动
对于直线运动中,建立一维坐标,据运动规律,就可以确定任意时刻的位置,进而知道它的运动轨迹。如果研究复杂的运动,我们怎么办呢?
02
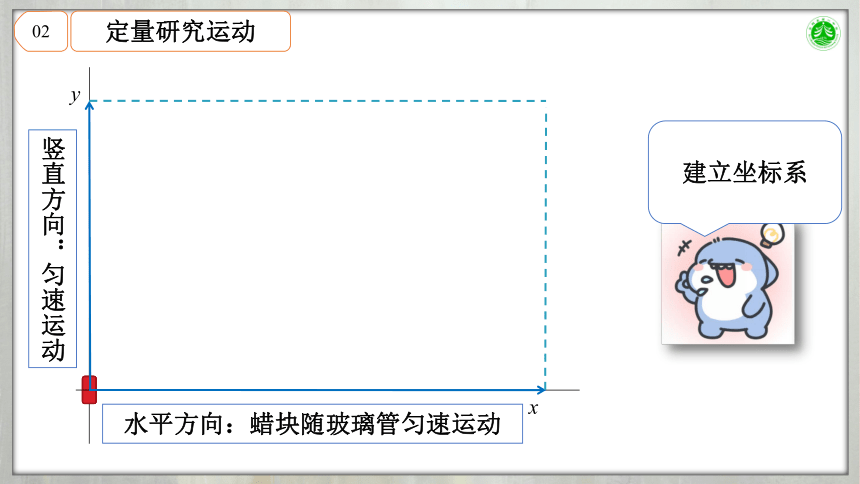
定量研究运动
水平方向:蜡块随玻璃管匀速运动
竖直方向:匀速运动
y
x
建立坐标系
02
定量研究运轨迹
水平方向:蜡块随玻璃管匀速运动
竖直方向:匀速运动
y
x
经过时间t
水平方向:x=vxt
竖直方向:y=vyt
消去变量t,实际运动轨迹:
结论:蜡块的运动轨迹
是条直线
定值
02
定量研究运动速度
水平方向:蜡块随玻璃管匀速运动
竖直方向:匀速运动
y
x
经过时间t
实际速度大小
结论:蜡块的运动是
匀速直线运动
实际速度方向
vy
vx
v
θ
这些运动与物体的实际运动之间又有什么关系呢?
试一试
2. 在许多情况下,跳伞员跳伞后最初一段时间降落伞并不张开,跳伞员做加速运动。随后,降落伞张开,跳伞员做减速运动。速度减小到一定值后便不再减小,跳伞员以这一速度做匀速运动,直至落地。无风时某跳伞员竖直下落,着地时速度是5 m/s。现在有风,运动员在竖直方向的运动情况与无风时相同,并且风使他以4 m/s 的速度沿水平方向运动。跳伞员将以多大速度着地?画出速度合成的图示。
01
合运动与分运动
实际发生的运动(合运动)
竖直方向分运动
水平方向分运动
02
合运动与分运动的特征
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
合运动
分运动
分运动
03
运动的合成与分解
合运动
分运动
运动的合成
运动的分解
⑴分解原则:根据运动的实际效果分解,也可以正交分解。
⑵遵循规律:平行四边形法则
03
运动的合成与分解
a
a1
a2
v1
v2
v
运动的合成与分解是指 x、v、 a 的合成与分解。
A
B
x
x1
x2
位移的合成
速度的合成
加速度的合成
运动的合成是唯一的,而分解不是唯一
【例题】某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是 0.15m,自动扶梯与水平面的夹角为 30°,自动扶梯前进的速度是 0.76m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼。哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
【解析】如图所示,甲在竖直方向的速度
乙在竖直方向的速度
因此v甲y > v乙,甲先到楼上
甲比乙先到达楼上,甲上楼用了12 s。
思考与讨论
匀速
匀加速
轨迹?
思考与讨论
匀速
匀加速
v1
v2
每隔2秒连续拍照,并进行合成
思考与讨论
计算机模拟运动情况
试一试
假设从某时刻(t = 0)开始,红蜡块在玻璃管内每1 s 上升的距离都是10 cm,与此同时,玻璃管向右沿水平方向匀加速平移,每1 s 内的位移依次是4 cm、12 cm、20 cm、28 cm。在图5.2-7 所示的坐标系中,y 表示蜡块在竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t = 0 时蜡块位于坐标原点。请在图中标出t等于1 s、2 s、3 s、4 s 时蜡块的位置,并用平滑曲线描绘蜡块的轨迹。
01
不共线分运动的合成
(1)两个都是从静止开始的互成角度匀加速直线运动的合运动是什么运动?
(2)两个初速度都不为零互成角度匀加速直线运动的合运动是什么运动?
一定是匀加速直线运动
可能是匀变速直线运动,也有可能是匀变速曲线运动
v
v2
v1
a1
a2
a
v
v2
v1
a1
a2
a
判断轨迹的关键:看合加速度、合速度是否在一条直线上。
01
小船过河模型
船的实际运动就是合运动。
v合:船的实际运动 (相对于河岸的运动)
v水:水漂流的运动和以速度
v船 船相对于静水的划行运动的速度。
01
小船过河模型
v合= v船+ v水
02
小船过河时间
d
当v船 与河岸夹角为θ时,渡河时间:
v船
v水
t=
v船sinθ1
d
θ1
sinθ1取最大时时间t有最小值
02
小船过河最短时间
d
因此当v船 垂直于河岸时,渡河时间最短:
v船
v水
tmin=
v船
d
v
θ
tanθ=
v水
v船
03
小船过河最短位移
d
当合速度v 方向垂直于河岸时,渡河位移最短,且为河宽d 。
v船
θ
v水
渡河时间:
t = =
v
d
v船 sinθ
d
cosθ=
v船
v水
v
情景1:v船>v水
03
小船过河最短位移
d
当v船方向与合速度v 方向垂直时,有最短渡河位移lmin 。
最短位移:
t =
v
lmin
cosθ=
v水
v船
v水
lmin
lmin=
cosθ
d
B
C
D
E
A
v船
θ
θ
θ
渡河时间:
v
v船
情景2:v船01
关联速度
1.“关联速度”特点:用绳、杆相牵连的物体,在运动过程中,两物体的速度通常不同,但物体沿绳或杆方向的速度分量大小相等。
丙 丁
甲 乙
2.常见的模型:
02
关联速度问题
如图,绳以恒定速率v 沿水平方向通过定滑轮牵引小船靠岸,当绳与水面夹角为θ 时,船的速度为多大?
v
θ
A
B
C
v∥
沿绳
垂直于绳
v⊥
v船
若要使船匀速靠岸,则拉绳的速度v有何特点?(匀速?加速?减速?)
A
03
关联速度解题步骤
1.先确定合运动,物体的实际运动就是合运动。
2.确定合运动的两个实际作用效果:一方面是使绳或杆伸缩的效果,另一方面是使绳或杆转动的效果。
3.按平行四边形定则进行分解(沿绳或杆方向的分速度和垂直于绳或杆方向的分速度)。
4.根据沿绳或杆牵引方向的速度相等。
解题关键:找到真正的合速度(实际速度)
04
系统集成练习
D
04
系统集成练习
C
课堂小结
分运动
合运动
运动的合成
运动的分解
分速度
分位移
分加速度
合成
分解
合速度
合位移
合加速度
运动的合成与分解遵循平行四边形定则
小船过河
关联速度
新课导入
军事演习过程中投掷物资是在目标上空投放还是在离目标有一段距离时提前投放,为什么?
如何研究这一类运动呢
01
观察红蜡块的运动
观察:
蜡块在做什么样的运动?
它的轨迹是直线还是曲线?
01
观察红蜡块的运动
1、蜡块A沿玻璃管匀速上升。
01
观察红蜡块的运动
2、蜡块A匀速向右。
01
观察红蜡块的运动
3、蜡块合运动情况。
02
定量研究运动
对于直线运动中,建立一维坐标,据运动规律,就可以确定任意时刻的位置,进而知道它的运动轨迹。如果研究复杂的运动,我们怎么办呢?
02
定量研究运动
水平方向:蜡块随玻璃管匀速运动
竖直方向:匀速运动
y
x
建立坐标系
02
定量研究运轨迹
水平方向:蜡块随玻璃管匀速运动
竖直方向:匀速运动
y
x
经过时间t
水平方向:x=vxt
竖直方向:y=vyt
消去变量t,实际运动轨迹:
结论:蜡块的运动轨迹
是条直线
定值
02
定量研究运动速度
水平方向:蜡块随玻璃管匀速运动
竖直方向:匀速运动
y
x
经过时间t
实际速度大小
结论:蜡块的运动是
匀速直线运动
实际速度方向
vy
vx
v
θ
这些运动与物体的实际运动之间又有什么关系呢?
试一试
2. 在许多情况下,跳伞员跳伞后最初一段时间降落伞并不张开,跳伞员做加速运动。随后,降落伞张开,跳伞员做减速运动。速度减小到一定值后便不再减小,跳伞员以这一速度做匀速运动,直至落地。无风时某跳伞员竖直下落,着地时速度是5 m/s。现在有风,运动员在竖直方向的运动情况与无风时相同,并且风使他以4 m/s 的速度沿水平方向运动。跳伞员将以多大速度着地?画出速度合成的图示。
01
合运动与分运动
实际发生的运动(合运动)
竖直方向分运动
水平方向分运动
02
合运动与分运动的特征
等时性 各分运动与合运动同时发生和结束,时间相同
等效性 各分运动的共同效果与合运动的效果相同
同体性 各分运动与合运动是同一物体的运动
独立性 各分运动之间互不相干,彼此独立,互不影响
合运动
分运动
分运动
03
运动的合成与分解
合运动
分运动
运动的合成
运动的分解
⑴分解原则:根据运动的实际效果分解,也可以正交分解。
⑵遵循规律:平行四边形法则
03
运动的合成与分解
a
a1
a2
v1
v2
v
运动的合成与分解是指 x、v、 a 的合成与分解。
A
B
x
x1
x2
位移的合成
速度的合成
加速度的合成
运动的合成是唯一的,而分解不是唯一
【例题】某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是 0.15m,自动扶梯与水平面的夹角为 30°,自动扶梯前进的速度是 0.76m/s。有甲、乙两位顾客,分别从自动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上以每秒上两个台阶的速度匀速上楼。哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
【解析】如图所示,甲在竖直方向的速度
乙在竖直方向的速度
因此v甲y > v乙,甲先到楼上
甲比乙先到达楼上,甲上楼用了12 s。
思考与讨论
匀速
匀加速
轨迹?
思考与讨论
匀速
匀加速
v1
v2
每隔2秒连续拍照,并进行合成
思考与讨论
计算机模拟运动情况
试一试
假设从某时刻(t = 0)开始,红蜡块在玻璃管内每1 s 上升的距离都是10 cm,与此同时,玻璃管向右沿水平方向匀加速平移,每1 s 内的位移依次是4 cm、12 cm、20 cm、28 cm。在图5.2-7 所示的坐标系中,y 表示蜡块在竖直方向的位移,x表示蜡块随玻璃管通过的水平位移,t = 0 时蜡块位于坐标原点。请在图中标出t等于1 s、2 s、3 s、4 s 时蜡块的位置,并用平滑曲线描绘蜡块的轨迹。
01
不共线分运动的合成
(1)两个都是从静止开始的互成角度匀加速直线运动的合运动是什么运动?
(2)两个初速度都不为零互成角度匀加速直线运动的合运动是什么运动?
一定是匀加速直线运动
可能是匀变速直线运动,也有可能是匀变速曲线运动
v
v2
v1
a1
a2
a
v
v2
v1
a1
a2
a
判断轨迹的关键:看合加速度、合速度是否在一条直线上。
01
小船过河模型
船的实际运动就是合运动。
v合:船的实际运动 (相对于河岸的运动)
v水:水漂流的运动和以速度
v船 船相对于静水的划行运动的速度。
01
小船过河模型
v合= v船+ v水
02
小船过河时间
d
当v船 与河岸夹角为θ时,渡河时间:
v船
v水
t=
v船sinθ1
d
θ1
sinθ1取最大时时间t有最小值
02
小船过河最短时间
d
因此当v船 垂直于河岸时,渡河时间最短:
v船
v水
tmin=
v船
d
v
θ
tanθ=
v水
v船
03
小船过河最短位移
d
当合速度v 方向垂直于河岸时,渡河位移最短,且为河宽d 。
v船
θ
v水
渡河时间:
t = =
v
d
v船 sinθ
d
cosθ=
v船
v水
v
情景1:v船>v水
03
小船过河最短位移
d
当v船方向与合速度v 方向垂直时,有最短渡河位移lmin 。
最短位移:
t =
v
lmin
cosθ=
v水
v船
v水
lmin
lmin=
cosθ
d
B
C
D
E
A
v船
θ
θ
θ
渡河时间:
v
v船
情景2:v船
关联速度
1.“关联速度”特点:用绳、杆相牵连的物体,在运动过程中,两物体的速度通常不同,但物体沿绳或杆方向的速度分量大小相等。
丙 丁
甲 乙
2.常见的模型:
02
关联速度问题
如图,绳以恒定速率v 沿水平方向通过定滑轮牵引小船靠岸,当绳与水面夹角为θ 时,船的速度为多大?
v
θ
A
B
C
v∥
沿绳
垂直于绳
v⊥
v船
若要使船匀速靠岸,则拉绳的速度v有何特点?(匀速?加速?减速?)
A
03
关联速度解题步骤
1.先确定合运动,物体的实际运动就是合运动。
2.确定合运动的两个实际作用效果:一方面是使绳或杆伸缩的效果,另一方面是使绳或杆转动的效果。
3.按平行四边形定则进行分解(沿绳或杆方向的分速度和垂直于绳或杆方向的分速度)。
4.根据沿绳或杆牵引方向的速度相等。
解题关键:找到真正的合速度(实际速度)
04
系统集成练习
D
04
系统集成练习
C
课堂小结
分运动
合运动
运动的合成
运动的分解
分速度
分位移
分加速度
合成
分解
合速度
合位移
合加速度
运动的合成与分解遵循平行四边形定则
小船过河
关联速度
