几类不同增长的函数模型
图片预览



文档简介
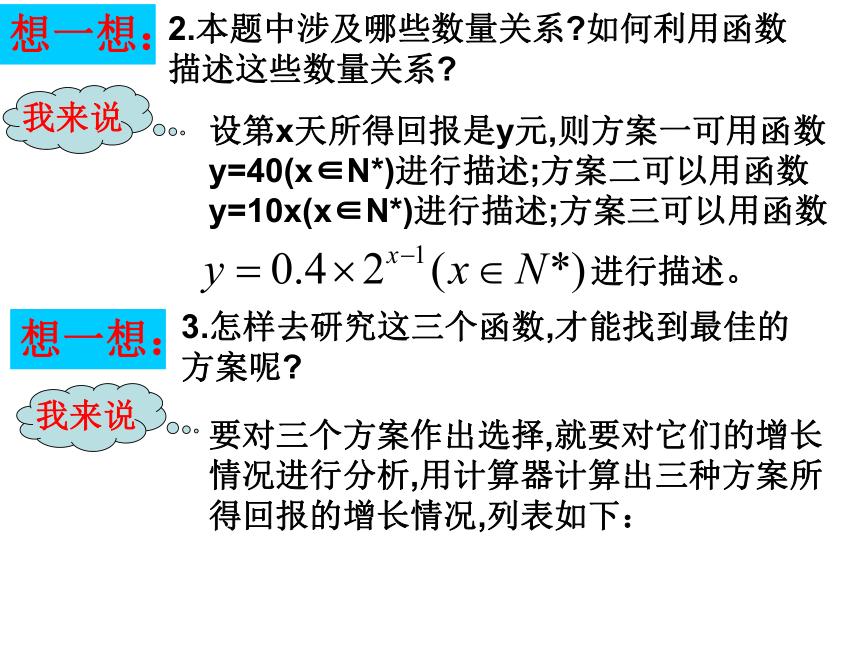
课件18张PPT。3.2.1 几类不同增长的函数模型 通过一些实例,来感受一次函数、二次函数、指数函数、对数函数以及幂函数的广泛应用;结合实例体会直线上升、指数爆炸、对数增长等不同增长的函数模型意义,理解它们的增长差异性.学习目标复习引入,创设情景我要问在我们的生活中,有没有用到函数的例子?我来答有.如:细胞分裂,汽车行驶的路程与时间的关系,……生活中,数学无处不在,用好数学,将会给我们带来很大的方便。今天我们就来看一个利用数学为我们服务的例子。互动交流,探求新知例1、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:回报的累积值方案二:第一天回报10元,以后每天比前一天多 回报10元;方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。请问,你会选择哪种投资方案呢?1.考虑回报量,除了要考虑每天的回报量之外,还得考虑什么?想一想:方案一:每天回报40元;我来说想一想:2.本题中涉及哪些数量关系?如何利用函数描述这些数量关系?我来说设第x天所得回报是y元,则方案一可用函数y=40(x∈N*)进行描述;方案二可以用函数y=10x(x∈N*)进行描述;方案三可以用函数
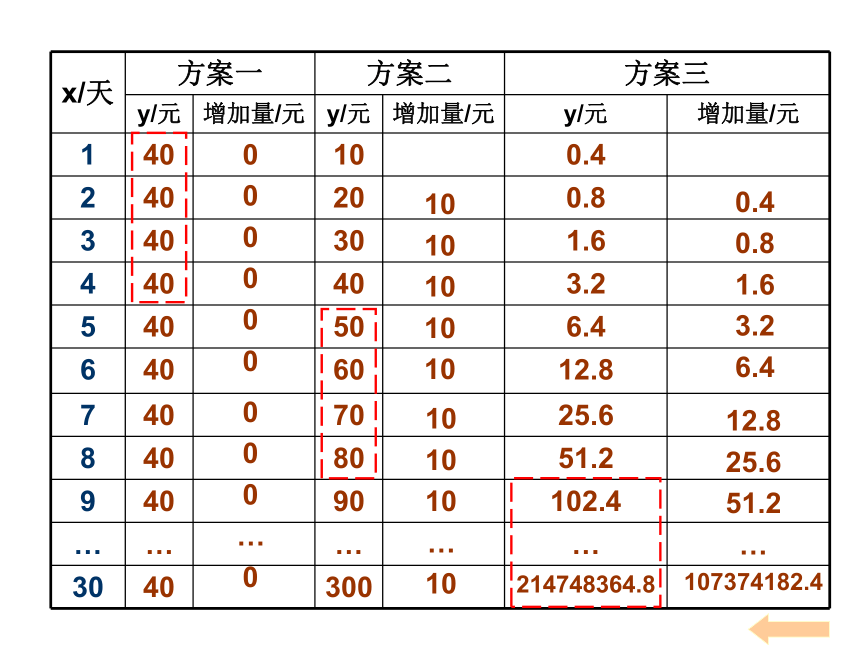
进行描述。想一想:3.怎样去研究这三个函数,才能找到最佳的方案呢?要对三个方案作出选择,就要对它们的增长情况进行分析,用计算器计算出三种方案所得回报的增长情况,列表如下:我来说0
0
0
0
0
00
0
0
…
010
10
10
10
1010
10
10
…
100.4
0.8
1.6
3.2
6.412.8
25.6
51.2
…
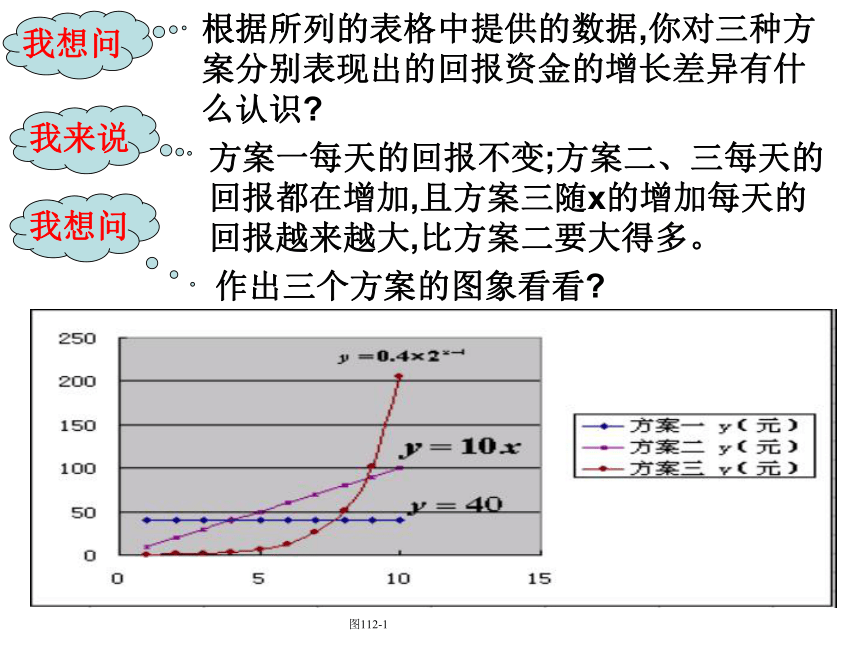
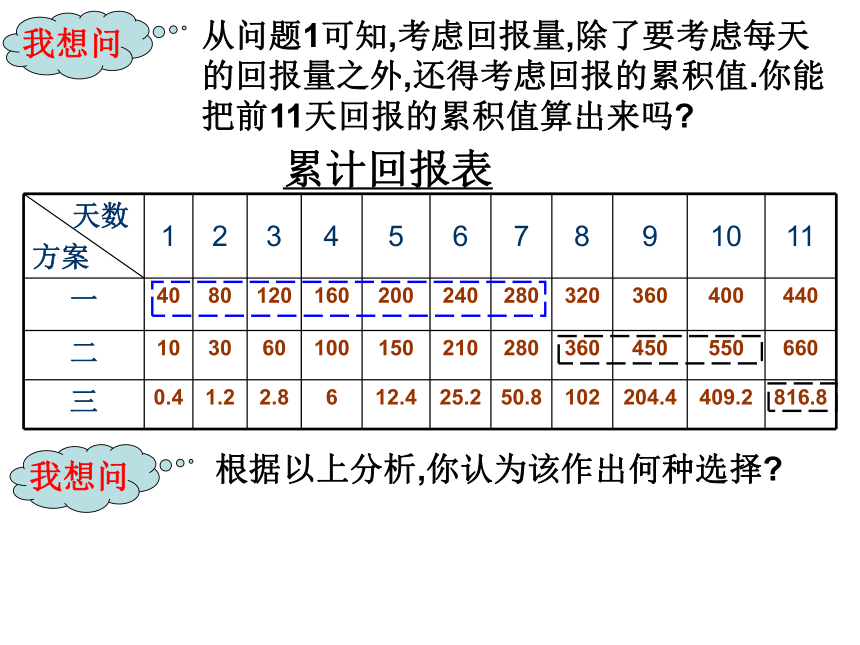
107374182.4我想问根据所列的表格中提供的数据,你对三种方案分别表现出的回报资金的增长差异有什么认识?我来说方案一每天的回报不变;方案二、三每天的回报都在增加,且方案三随x的增加每天的回报越来越大,比方案二要大得多。我想问作出三个方案的图象看看?图112-1我想问根据以上分析,你认为该作出何种选择?从问题1可知,考虑回报量,除了要考虑每天的回报量之外,还得考虑回报的累积值.你能把前11天回报的累积值算出来吗?累计回报表我想问结论: 投资8天以下(不含8天),应选择第一种投资方案;投资8~10天,应选择第二种投资方案;投资11天(含11天)以上,应选择第三种投资方案。解决实际问题的一般步骤是什么?例题的启示解决实际问题的步骤:实际问题读懂问题抽象概括数学问题演算推理数学问题的解还原说明实际问题的解例2、某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求呢?我想问本题中涉及了哪几类函数模型?实质是什么?本例涉及了一次函数、对数函数、指数函数三类函数模型,实质是比较三个函数的增长情况。我来说我再问怎样才能判断所给的奖励模型是否符合公司的要求呢?我来说要对每一个奖励模型的奖金总额是否超出5万元,以及奖励比例是否超过25%进行分析,才能做出正确选择。解:借助计算机作出三个函数的图象如下:对于模型y=0.25x,它在区间[10,1000]上递增,当x∈(20,1000)时,y>5,因此该模型不符合要求。对于模型 ,由函数图象,并利用计算器,可知在区间(805,806)内有一个点 满足 ,由于它在[10,1000]上递增,因此当 时,y>5,因此该模型也不符合要求。对于模型 ,它在区间[10,1000]上递增,而且当x=1000时, ,所以它符合奖金总数不超过5万元的要求。再计算按模型 奖励时,奖金是否不超过利润的25%,即当x∈[10,1000]时,是否有
成立。 令 ,x∈[10,1000],利用计算机作出函数f(x)的图象由图可知它是减函数,因此
f(x)即所以,当x∈[10,1000]时,说明按模型3奖励,奖金不超过利润的25%。
综上所述,模型 确实符合公司的要求。练习:P98 T1
限时4分钟练一练探究:你能否仿照前面例题使用的方法,探索研究幂函数 .
指数函数 .
对数函数
在区间(0,+∞)上的增长差异?结论一般地,对于指数函数 和幂函数通过探索可以发现,在区间(0,+∞)上,无论n比a大多少,尽管在x的一定变化范围内, 会小于 ,
但由于 的增长快于 的增长,因此,总存在一个 ,当 时,就会有同样地,对于对数函数 和幂函数
,在区间(0,+∞)上,随着x的增大,
增长得越来越慢,图象就像是渐渐地与x轴平行一样,尽管在x的一定变化范围内, 可能会大于 ,但由于 的增长慢于 的增长,因此,总存在一个 ,当 时,就会有综上所述在区间(0,+∞)上,尽管 , 和 都是增函数,但它们的增长速度不同,而且不在同一个"档次"上,随着x的增大, 的增长速度越来越快,会超过并远远大于的 增长速度,而
的增长速度则越来越慢.因此,总会存在一个 ,当 时,就有 随堂练习:P101练习小结实际
问题读懂问题将问题
抽象化数学
模型解决
问题基础过程关键目的几种常见函数的增长情况:作业:P107习题3.2 T1、2再见
进行描述。想一想:3.怎样去研究这三个函数,才能找到最佳的方案呢?要对三个方案作出选择,就要对它们的增长情况进行分析,用计算器计算出三种方案所得回报的增长情况,列表如下:我来说0
0
0
0
0
00
0
0
…
010
10
10
10
1010
10
10
…
100.4
0.8
1.6
3.2
6.412.8
25.6
51.2
…
107374182.4我想问根据所列的表格中提供的数据,你对三种方案分别表现出的回报资金的增长差异有什么认识?我来说方案一每天的回报不变;方案二、三每天的回报都在增加,且方案三随x的增加每天的回报越来越大,比方案二要大得多。我想问作出三个方案的图象看看?图112-1我想问根据以上分析,你认为该作出何种选择?从问题1可知,考虑回报量,除了要考虑每天的回报量之外,还得考虑回报的累积值.你能把前11天回报的累积值算出来吗?累计回报表我想问结论: 投资8天以下(不含8天),应选择第一种投资方案;投资8~10天,应选择第二种投资方案;投资11天(含11天)以上,应选择第三种投资方案。解决实际问题的一般步骤是什么?例题的启示解决实际问题的步骤:实际问题读懂问题抽象概括数学问题演算推理数学问题的解还原说明实际问题的解例2、某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求呢?我想问本题中涉及了哪几类函数模型?实质是什么?本例涉及了一次函数、对数函数、指数函数三类函数模型,实质是比较三个函数的增长情况。我来说我再问怎样才能判断所给的奖励模型是否符合公司的要求呢?我来说要对每一个奖励模型的奖金总额是否超出5万元,以及奖励比例是否超过25%进行分析,才能做出正确选择。解:借助计算机作出三个函数的图象如下:对于模型y=0.25x,它在区间[10,1000]上递增,当x∈(20,1000)时,y>5,因此该模型不符合要求。对于模型 ,由函数图象,并利用计算器,可知在区间(805,806)内有一个点 满足 ,由于它在[10,1000]上递增,因此当 时,y>5,因此该模型也不符合要求。对于模型 ,它在区间[10,1000]上递增,而且当x=1000时, ,所以它符合奖金总数不超过5万元的要求。再计算按模型 奖励时,奖金是否不超过利润的25%,即当x∈[10,1000]时,是否有
成立。 令 ,x∈[10,1000],利用计算机作出函数f(x)的图象由图可知它是减函数,因此
f(x)
综上所述,模型 确实符合公司的要求。练习:P98 T1
限时4分钟练一练探究:你能否仿照前面例题使用的方法,探索研究幂函数 .
指数函数 .
对数函数
在区间(0,+∞)上的增长差异?结论一般地,对于指数函数 和幂函数通过探索可以发现,在区间(0,+∞)上,无论n比a大多少,尽管在x的一定变化范围内, 会小于 ,
但由于 的增长快于 的增长,因此,总存在一个 ,当 时,就会有同样地,对于对数函数 和幂函数
,在区间(0,+∞)上,随着x的增大,
增长得越来越慢,图象就像是渐渐地与x轴平行一样,尽管在x的一定变化范围内, 可能会大于 ,但由于 的增长慢于 的增长,因此,总存在一个 ,当 时,就会有综上所述在区间(0,+∞)上,尽管 , 和 都是增函数,但它们的增长速度不同,而且不在同一个"档次"上,随着x的增大, 的增长速度越来越快,会超过并远远大于的 增长速度,而
的增长速度则越来越慢.因此,总会存在一个 ,当 时,就有 随堂练习:P101练习小结实际
问题读懂问题将问题
抽象化数学
模型解决
问题基础过程关键目的几种常见函数的增长情况:作业:P107习题3.2 T1、2再见
