第二十四章圆精选题(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
第二十四章圆精选题-数学九年级上册人教版
一、选择题
1.如图,是的直径,是上一点.若,则( )
A. B. C. D.
2.如图所示,直角三角尺阴影部分的面积是( )
A.ab B.ab﹣πr2 C.ab﹣πr2 D.ab﹣r2
3.已知⊙O的半径为2,点P在⊙O内,则OP的长可能是( )
A.1 B.2 C.3 D.4
4.若⊙P的半径为13,圆心P的坐标为(5, 12 ),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
5.如图,点A,B,C在⊙O上,连结AB,AC,OB,OC.若∠BAC=50°,则∠BOC的度数是( )
A.80° B.90° C.100° D.110°
6. 下列命题:①各边相等的多边形是正多边形;②正多边形是轴对称图形;③正六边形的每个外角均为60°;④正n边形有(n﹣3)条对角线.其中真命题的个数为( )
A.4 B.3 C.2 D.1
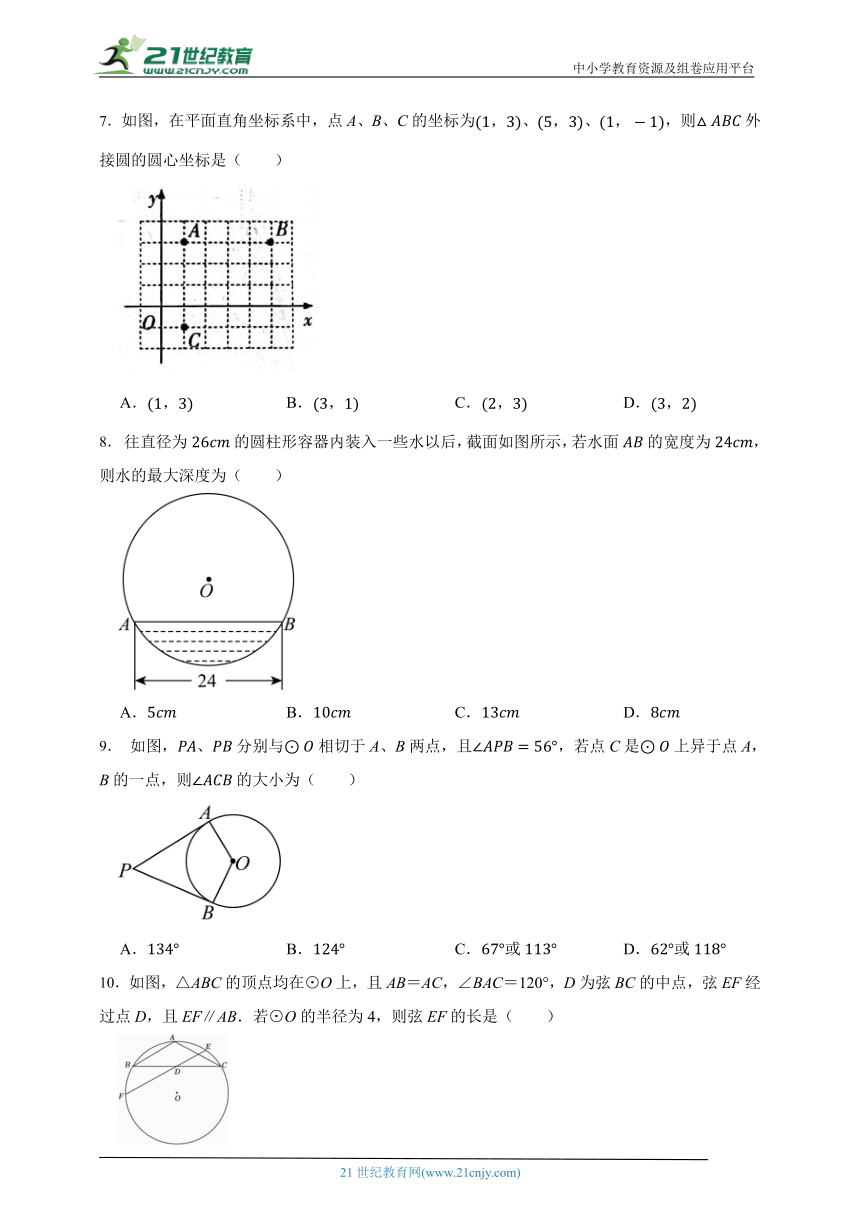
7.如图,在平面直角坐标系中,点A、B、C的坐标为、、,则外接圆的圆心坐标是( )
A. B. C. D.
8. 往直径为的圆柱形容器内装入一些水以后,截面如图所示,若水面的宽度为,则水的最大深度为( )
A. B. C. D.
9. 如图,、分别与相切于A、B两点,且,若点C是上异于点A,B的一点,则的大小为( )
A. B. C.或 D.或
10.如图,△ABC的顶点均在⊙O上,且AB=AC,∠BAC=120°,D为弦BC的中点,弦EF经过点D,且EF∥AB.若⊙O的半径为4,则弦EF的长是( )
A.3 B.2 C.2 D.2
二、填空题
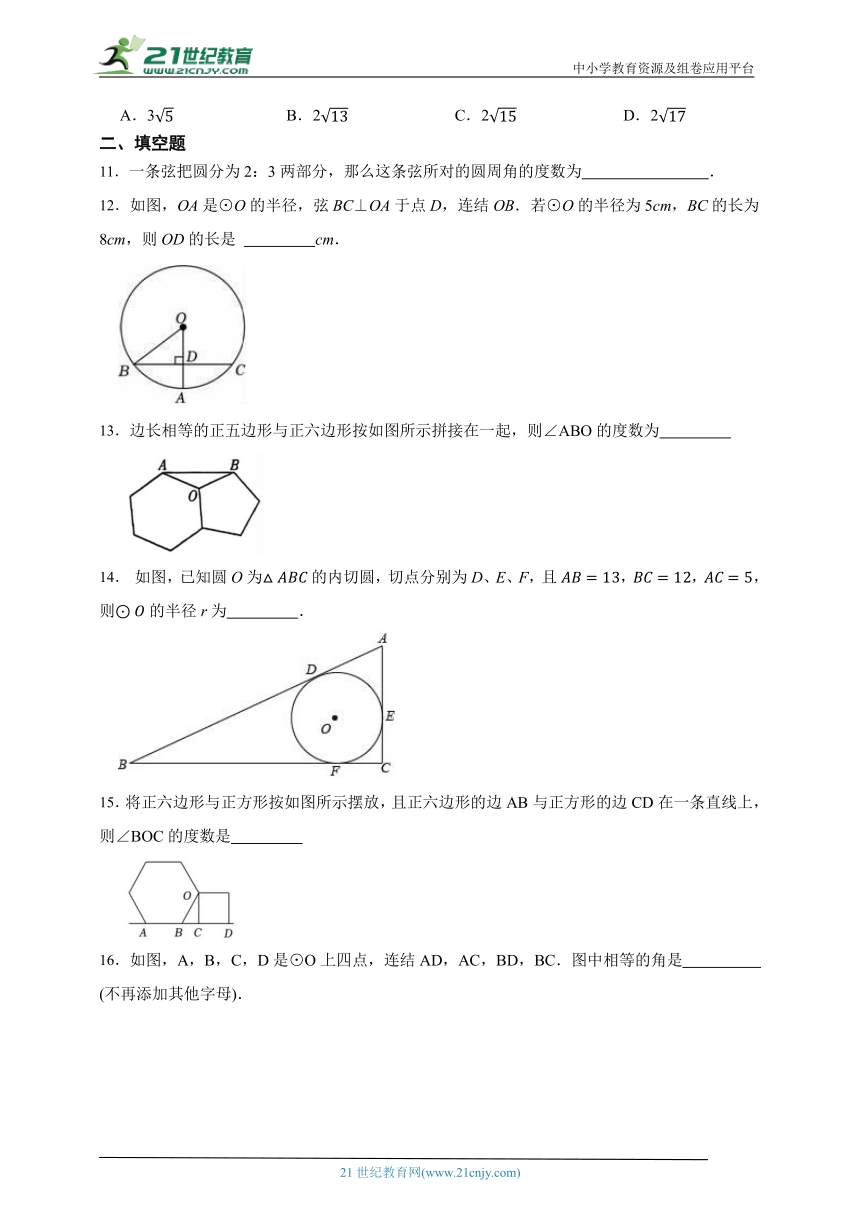
11.一条弦把圆分为2:3两部分,那么这条弦所对的圆周角的度数为 .
12.如图,OA是⊙O的半径,弦BC⊥OA于点D,连结OB.若⊙O的半径为5cm,BC的长为8cm,则OD的长是 cm.
13.边长相等的正五边形与正六边形按如图所示拼接在一起,则∠ABO的度数为
14. 如图,已知圆O为的内切圆,切点分别为D、E、F,且,,,则的半径r为 .
15.将正六边形与正方形按如图所示摆放,且正六边形的边AB与正方形的边CD在一条直线上,则∠BOC的度数是
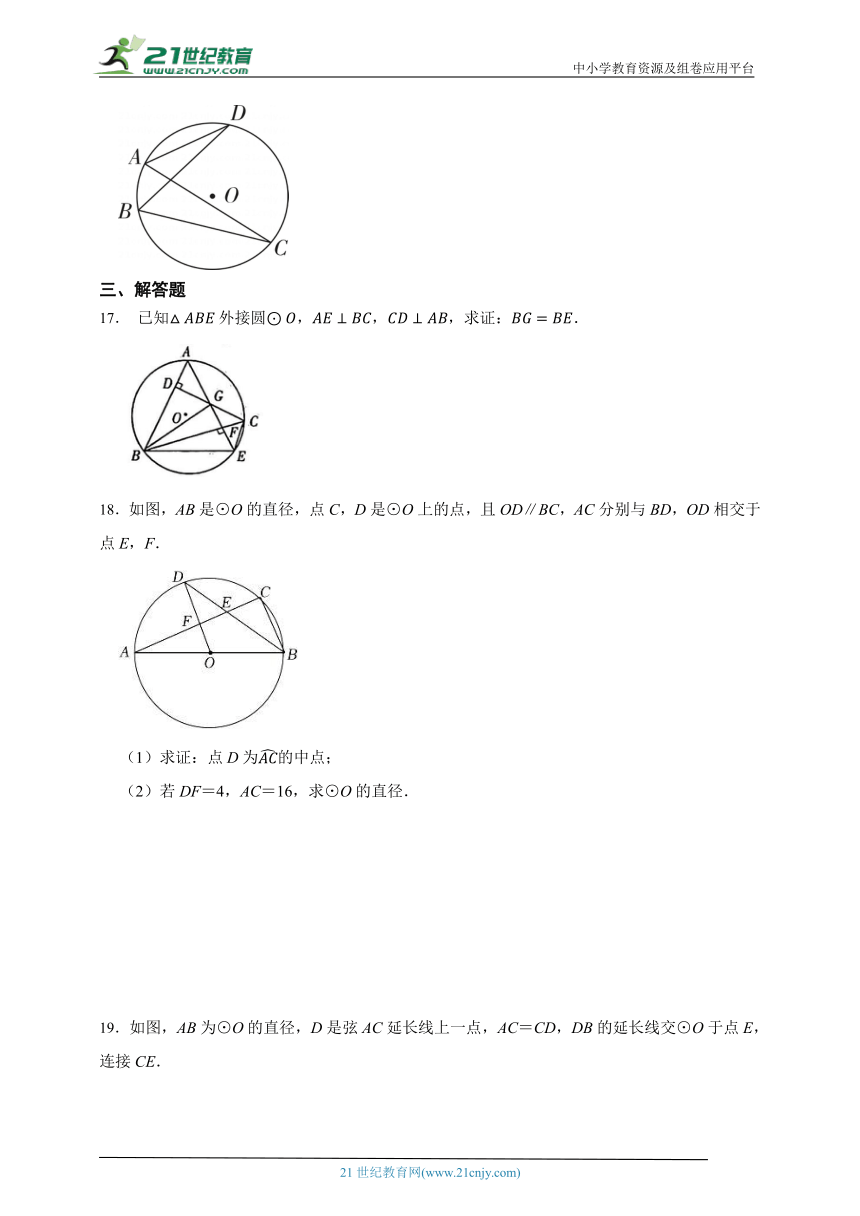
16.如图,A,B,C,D是⊙O上四点,连结AD,AC,BD,BC.图中相等的角是 (不再添加其他字母).
三、解答题
17. 已知外接圆,,,求证:.
18.如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为的中点;
(2)若DF=4,AC=16,求⊙O的直径.
19.如图,AB为⊙O的直径,D是弦AC延长线上一点,AC=CD,DB的延长线交⊙O于点E,连接CE.
(1)求证∠A=∠D;
(2)若的度数为108°,求∠E的度数.
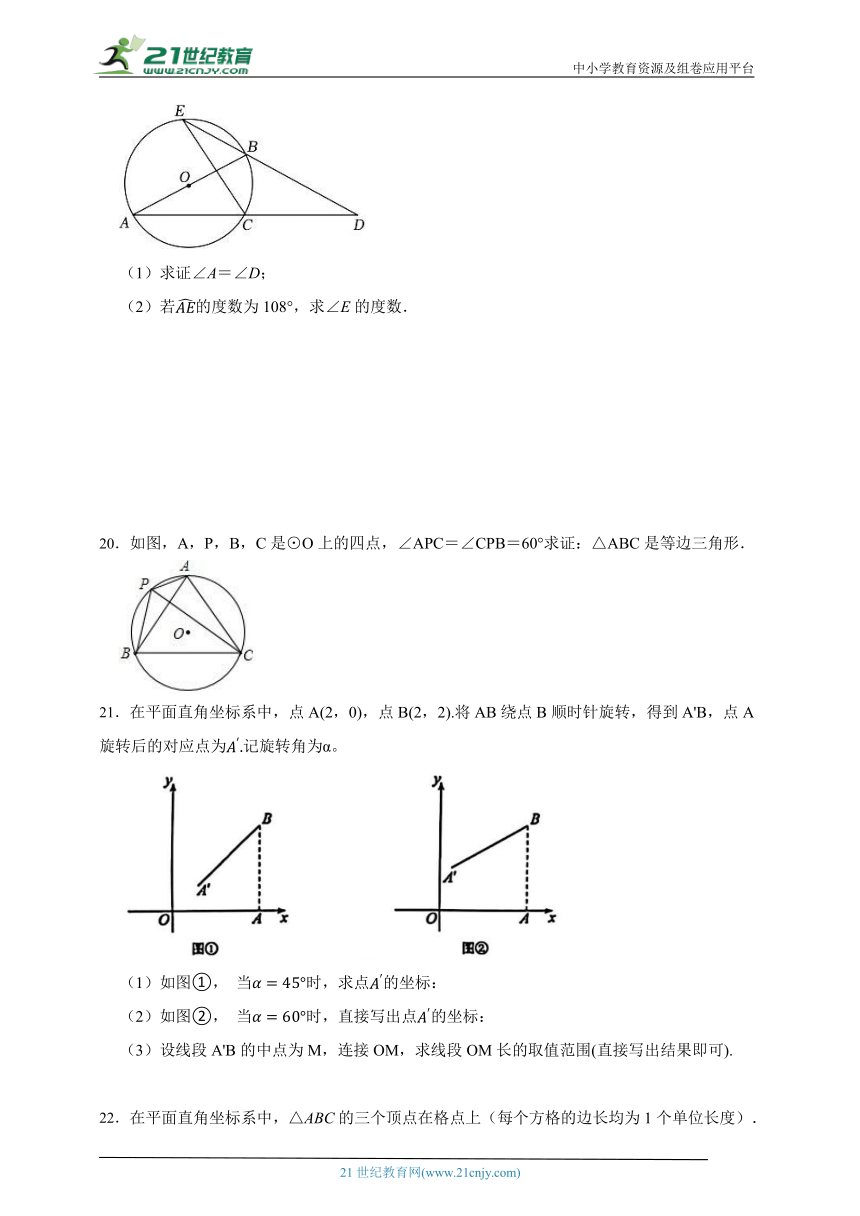
20.如图,A,P,B,C是⊙O上的四点,∠APC=∠CPB=60°求证:△ABC是等边三角形.
21.在平面直角坐标系中,点A(2,0),点B(2,2).将AB绕点B顺时针旋转,得到A'B,点A旋转后的对应点为记旋转角为α。
(1)如图①, 当时,求点的坐标:
(2)如图②, 当时,直接写出点的坐标:
(3)设线段A'B的中点为M,连接OM,求线段OM长的取值范围(直接写出结果即可).
22.在平面直角坐标系中,△ABC的三个顶点在格点上(每个方格的边长均为1个单位长度).
⑴请画出△ABC关于原点对称的图形△A1B1C1,并写出B1点的坐标.
⑵将△ABC绕点B逆时针旋转90°,画出旋转后得到的△A2B2C2;
⑶求(2)中点A移动的距离.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】72°或108°
12.【答案】3
13.【答案】24°
14.【答案】2
15.【答案】30°
16.【答案】∠A=∠B,∠C=∠D
17.【答案】解:设
与都是所对的圆周角,
又,,,
又,
证
由中垂直线定理(或其它的方法)得
18.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=∠C=90°,
∴OF⊥AC,
∴,
∴点D为的中点;
(2)解:∵OF⊥AC,
∴AF=AC=8,
在Rt△AFO中,AO2=AF2+OF2,
∴OA2=64+(OD﹣DF)2,
∴OA2=64+(OA﹣4)2,
∴OA=10,
∴⊙O的直径为20.
19.【答案】(1)证明:连接BC,
∵AB是⊙O的直径,
∴即AD⊥BC,
又AC=CD,
∴AB=BD,
∴∠A=∠D;
(2)解:∵的度数为108°,
∴∠EBA=54°,
又∠EBA=∠A+∠D,∠A=∠D,
∴,
∴∠E=∠A=27°.
20.【答案】证明:由圆周角定理得,∠ABC=∠CPB=60°,
∴△ABC是等边三角形
21.【答案】(1)解:过点A'分别作A'C⊥OA,A'D⊥AB,垂足分别为C, D.
可得矩形A'CAD, 得.
∵ 点A(2,0), 点B(2,2),
∴ OA=AB=2, ∠OAB=90°. ∵ A'B是AB绕点 B顺时针旋转得到的,
∵A'D⊥AB, ∴∠A'BD=∠BA'D=45°.
∴ 在等腰直角三角形A'DB中, 由勾股定理知
得
∴点A'的坐标为
(2)
(3)
22.【答案】解:⑴如图,△A1B1C1即为所求,B1点的坐标(﹣4,﹣2);
⑵如图,△A2B2C2;即为所求;
⑶∵AB==
∴点A移动的距离==π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章圆精选题-数学九年级上册人教版
一、选择题
1.如图,是的直径,是上一点.若,则( )
A. B. C. D.
2.如图所示,直角三角尺阴影部分的面积是( )
A.ab B.ab﹣πr2 C.ab﹣πr2 D.ab﹣r2
3.已知⊙O的半径为2,点P在⊙O内,则OP的长可能是( )
A.1 B.2 C.3 D.4
4.若⊙P的半径为13,圆心P的坐标为(5, 12 ),则平面直角坐标系的原点O与⊙P的位置关系是( )
A.在⊙P内 B.在⊙P上 C.在⊙P外 D.无法确定
5.如图,点A,B,C在⊙O上,连结AB,AC,OB,OC.若∠BAC=50°,则∠BOC的度数是( )
A.80° B.90° C.100° D.110°
6. 下列命题:①各边相等的多边形是正多边形;②正多边形是轴对称图形;③正六边形的每个外角均为60°;④正n边形有(n﹣3)条对角线.其中真命题的个数为( )
A.4 B.3 C.2 D.1
7.如图,在平面直角坐标系中,点A、B、C的坐标为、、,则外接圆的圆心坐标是( )
A. B. C. D.
8. 往直径为的圆柱形容器内装入一些水以后,截面如图所示,若水面的宽度为,则水的最大深度为( )
A. B. C. D.
9. 如图,、分别与相切于A、B两点,且,若点C是上异于点A,B的一点,则的大小为( )
A. B. C.或 D.或
10.如图,△ABC的顶点均在⊙O上,且AB=AC,∠BAC=120°,D为弦BC的中点,弦EF经过点D,且EF∥AB.若⊙O的半径为4,则弦EF的长是( )
A.3 B.2 C.2 D.2
二、填空题
11.一条弦把圆分为2:3两部分,那么这条弦所对的圆周角的度数为 .
12.如图,OA是⊙O的半径,弦BC⊥OA于点D,连结OB.若⊙O的半径为5cm,BC的长为8cm,则OD的长是 cm.
13.边长相等的正五边形与正六边形按如图所示拼接在一起,则∠ABO的度数为
14. 如图,已知圆O为的内切圆,切点分别为D、E、F,且,,,则的半径r为 .
15.将正六边形与正方形按如图所示摆放,且正六边形的边AB与正方形的边CD在一条直线上,则∠BOC的度数是
16.如图,A,B,C,D是⊙O上四点,连结AD,AC,BD,BC.图中相等的角是 (不再添加其他字母).
三、解答题
17. 已知外接圆,,,求证:.
18.如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为的中点;
(2)若DF=4,AC=16,求⊙O的直径.
19.如图,AB为⊙O的直径,D是弦AC延长线上一点,AC=CD,DB的延长线交⊙O于点E,连接CE.
(1)求证∠A=∠D;
(2)若的度数为108°,求∠E的度数.
20.如图,A,P,B,C是⊙O上的四点,∠APC=∠CPB=60°求证:△ABC是等边三角形.
21.在平面直角坐标系中,点A(2,0),点B(2,2).将AB绕点B顺时针旋转,得到A'B,点A旋转后的对应点为记旋转角为α。
(1)如图①, 当时,求点的坐标:
(2)如图②, 当时,直接写出点的坐标:
(3)设线段A'B的中点为M,连接OM,求线段OM长的取值范围(直接写出结果即可).
22.在平面直角坐标系中,△ABC的三个顶点在格点上(每个方格的边长均为1个单位长度).
⑴请画出△ABC关于原点对称的图形△A1B1C1,并写出B1点的坐标.
⑵将△ABC绕点B逆时针旋转90°,画出旋转后得到的△A2B2C2;
⑶求(2)中点A移动的距离.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】72°或108°
12.【答案】3
13.【答案】24°
14.【答案】2
15.【答案】30°
16.【答案】∠A=∠B,∠C=∠D
17.【答案】解:设
与都是所对的圆周角,
又,,,
又,
证
由中垂直线定理(或其它的方法)得
18.【答案】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=∠C=90°,
∴OF⊥AC,
∴,
∴点D为的中点;
(2)解:∵OF⊥AC,
∴AF=AC=8,
在Rt△AFO中,AO2=AF2+OF2,
∴OA2=64+(OD﹣DF)2,
∴OA2=64+(OA﹣4)2,
∴OA=10,
∴⊙O的直径为20.
19.【答案】(1)证明:连接BC,
∵AB是⊙O的直径,
∴即AD⊥BC,
又AC=CD,
∴AB=BD,
∴∠A=∠D;
(2)解:∵的度数为108°,
∴∠EBA=54°,
又∠EBA=∠A+∠D,∠A=∠D,
∴,
∴∠E=∠A=27°.
20.【答案】证明:由圆周角定理得,∠ABC=∠CPB=60°,
∴△ABC是等边三角形
21.【答案】(1)解:过点A'分别作A'C⊥OA,A'D⊥AB,垂足分别为C, D.
可得矩形A'CAD, 得.
∵ 点A(2,0), 点B(2,2),
∴ OA=AB=2, ∠OAB=90°. ∵ A'B是AB绕点 B顺时针旋转得到的,
∵A'D⊥AB, ∴∠A'BD=∠BA'D=45°.
∴ 在等腰直角三角形A'DB中, 由勾股定理知
得
∴点A'的坐标为
(2)
(3)
22.【答案】解:⑴如图,△A1B1C1即为所求,B1点的坐标(﹣4,﹣2);
⑵如图,△A2B2C2;即为所求;
⑶∵AB==
∴点A移动的距离==π.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
